7.2.2 - Proportion 'Greater Than'

7.2.2 - Proportion 'Greater Than'

The following two examples use Minitab to find the area under a normal distribution that is greater than a given value. The first example uses the standard normal distribution (i.e., z distribution), which has a mean of 0 and standard deviation of 1; this is the default when first constructing a probability distribution plot in Minitab. The second example models a normal distribution with a mean of 65 and standard deviation of 5.

Later in this lesson we'll see that these methods can be used to identify p values when conducting right-tailed hypothesis tests.

Minitab®  – Proportion Greater Than a Value on a Normal Distribution

Question: What proportion of the standard normal distribution is greater than a z score of 2?

Recall that the standard normal distribution (i.e., z distribution) has a mean of 0 and standard deviation of 1. This is the default normal distribution in Minitab.

Steps
  1. From the tool bar select Graph > Probability Distribution Plot > One Curve > View Probability
  2. Check that the Mean is 0 and the Standard deviation is 1
  3. Select Options
  4. Select A specified x value
  5. Select Right tail
  6. For X value enter 2
  7. Click Ok
  8. Click Ok

This should result in the following output:

  Distribution Plot Normal, Mean=0, StDev=1 0.0 0.02275 0.1 0.2 0.3 0.4 2 0 X Density  

The area of the z distribution that is greater than 2 is 0.02275.

This could also be written in probability notation as P(z > 2) = 0.02275.

Video Walkthrough

Minitab®  – Proportion Greater Than a Value on a Normal Distribution

Question: Vehicle speeds at a highway location have a normal distribution with a mean of 65 mph and a standard deviation of 5 mph. What is the probability that a randomly selected vehicle will be going more than 73 mph? 

Let's construct a normal distribution with a mean of 65 and standard deviation of 5 to find the area greater than 73.

To calculate a probability for values greater than a given value in Minitab:

Steps
  1. From the tool bar select Graph > Probability Distribution Plot > One Curve > View Probability
  2. Change the Mean to 65 and the Standard deviation to 5
  3. Select Options
  4. Select A specified x value
  5. Select Right tail
  6. For X value enter 73
  7. Click Ok
  8. Click Ok

This should result in the following output:

  Distribution Plot Normal, Mean=65, StDev=5 0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.05480 73 65 X Density  

On a normal distribution with a mean of 65 and standard deviation of 5, the proportion greater than 73 is 0.05480.

In other words, 5.480% of vehicles will be going more than 73 mph.

Video Walkthrough

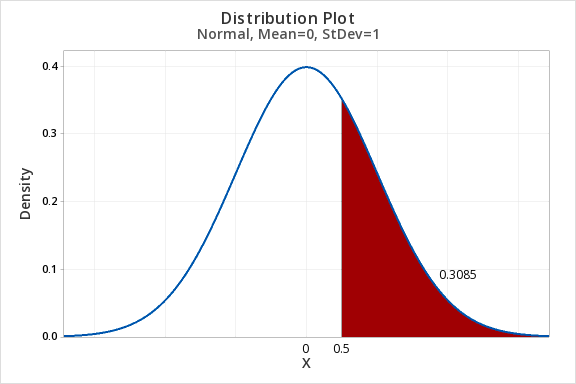
7.2.2.1 - Example: P(Z>0.5)

7.2.2.1 - Example: P(Z>0.5)

Question: What proportion of the z distribution is greater than z = 0.5?

Steps
  1. In Minitab select Graph > Probability Distribution Plot > One Curve > View Probability, hit OK.
  2. Select Normal and enter 0 for the mean and 1 for the standard deviation.(Note: The default is the standard normal distribution)
  3. Select Options
  4. Select A specified x value
  5. Select Right Tail
  6. For X value enter 0.5
  7. Click OK

    The proportion of the z distributions that falls above 0.5 is 0.3085.
    z distribution showing the proportion under the curve greater than 0.5
    Legend
    [1]Link
    ↥Has Tooltip/Popover
     Toggleable Visibility