7.2.3 - Proportion 'In between'

7.2.3 - Proportion 'In between'

In the following examples we will use Minitab to find the area under a normal distribution between two values. The first example uses the z distribution and the second example uses a normal distribution with a mean of 65 and standard deviation of 5.

Minitab®  – Area Between Two z Values

Question: What proportion of the standard normal distribution is between a z score of 0 and a z score of 1.75?

Recall that the standard normal distribution (i.e., z distribution) has a mean of 0 and standard deviation of 1. This is the default normal distribution in Minitab.

Steps
  1. From the tool bar select Graph > Probability Distribution Plot > One Curve > View Probability
  2. Check that the Mean is 0 and the Standard deviation is 1
  3. Select Options
  4. Select A specified x value
  5. Select Middle
  6. For X value 1 enter 0
  7. For X value 2 enter 1.75
  8. Click Ok
  9. Click Ok

This should result in the following output:

  Distribution Plot Normal, Mean=0, StDev=1 0.0 0.4599 0.1 0.2 0.3 0.4 1.75 0 X Density  

The proportion of the z distribution that is between 0 and 1.75 is 0.4599.

In probability notation, this could be written as P(0 ≤ z ≤ 1.75) = 0.4599

Video Walkthrough

Minitab®

Area Between Two Values on a Normal Distribution

Question: Vehicle speeds at a highway location have a normal distribution with a mean of 65 mph and a standard deviation of 5 mph. What is the probability that a randomly selected vehicle will be going between 60 mph and 73 mph?

Let's construct a normal distribution with a mean of 65 and standard deviation of 5 to find the area between 60 and 73.

Steps
  1. From the tool bar select Graph > Probability Distribution Plot > One Curve > View Probability
  2. Change the Mean to 65 and the Standard deviation to 5
  3. Select Options
  4. Select A specified x value
  5. Select Middle
  6. For X value 1 enter 60
  7. For X value 2 enter 73
  8. Click Ok
  9. Click Ok

This should result in the following output:

  Distribution Plot Normal, Mean=65, StDev=5 0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.7865 73 60 65 X Density  

On a normal distribution with a mean of 65 mph and standard deviation of 5 mph, the proportion of observations between 60 mph and 73 mph is 0.7865.

In other words, 78.65% of vehicles will be going between 60 mph and 73 mph. 

Video Walkthrough

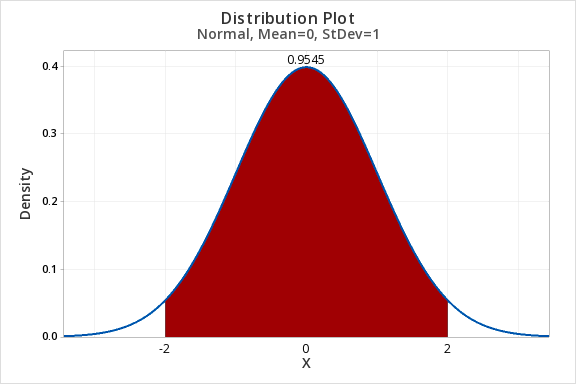
7.2.3.1 - Example: Proportion Between z -2 and +2

7.2.3.1 - Example: Proportion Between z -2 and +2

Question: What proportion of the z distribution is between -2 and 2?

Steps
  1. In Minitab select Graph > Probability Distribution Plot > One Curve > View Probability, hit OK.
  2. Select Normal and enter 0 for the mean and 1 for the standard deviation.(Note: The default is the standard normal distribution)
  3. Select Options
  4. Select A specified x value
  5. Select Middle and enter
    • X value 1: -2
    • X value 2: 2
  6. Select OK

    The proportion of the z distributions that falls between -2 and 2 is 0.9545.
    Legend
    [1]Link
    ↥Has Tooltip/Popover
     Toggleable Visibility