8.1.2.1.2 - Example: Handedness

Research Question: Are more than 80% of American's right handed?

In a sample of 100 Americans, 87 were right handed.

\(np_0 = 100(0.80)=80\)

\(n(1-p_0) = 100 (1-0.80) = 20\)

Both \(np_0\) and \(n(1-p_0)\) are at least 10 so we can use the normal approximation method. 

This is a right-tailed test because we want to know if the proportion is greater than 0.80.

\(H_{0}\colon p=0.80\)
\(H_{a}\colon p>0.80\)

\(\widehat{p}=\dfrac{87}{100}=0.87\), \(p_{0}=0.80\), \(n=100\)

\(z= \dfrac{\widehat{p}- p_0 }{\sqrt{\frac{p_0 (1- p_0)}{n}}}= \dfrac{0.87-0.80}{\sqrt{\frac{0.80 (1-0.80)}{100}}}=1.75\)

Our \(z\) test statistic is 1.75.

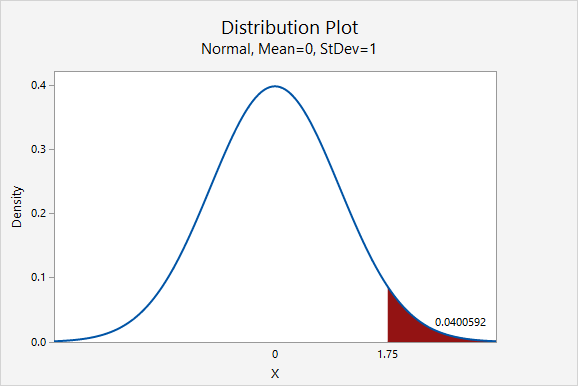
This is a right-tailed test so we need to find the area to the right of the test statistic, \(z=1.75\), on the z distribution.

Using Minitab , we find the probability \(P(z\geq1.75)=0.0400592\) which may be rounded to \(p\; value=0.0401\).

\(p\leq .05\), therefore our decision is to reject the null hypothesis

Yes, there is convincing evidence to state that more than 80% of all Americans are right handed.