8.1.2.1.3 - Example: Ice Cream

Research Question: Is the percentage of Creamery customers who prefer chocolate ice cream over vanilla less than 80%?

In a sample of 50 customers 60% preferred chocolate over vanilla.

1. Check assumptions and write hypotheses

\(np_0 = 50(0.80) = 40\)

\(n(1-p_0)=50(1-0.80) = 10\)

Both \(np_0\) and \(n(1-p_0)\) are at least 10. We can use the normal approximation method.

This is a left-tailed test because we want to know if the proportion is less than 0.80.

\(H_{0}\colon p=0.80\)
\(H_{a}\colon p<0.80\)

2. Calculate the test statistic

Test statistic: One Group Proportion

\(z=\dfrac{\widehat{p}- p_0 }{\sqrt{\frac{p_0 (1- p_0)}{n}}}\)

\(\widehat{p}\) = sample proportion
\(p_{0}\) = hypothesize population proportion
\(n\) = sample size

\(\widehat{p}=0.60\), \(p_{0}=0.80\), \(n=50\)

\(z= \dfrac{\widehat{p}- p_0 }{\sqrt{\frac{p_0 (1- p_0)}{n}}}= \dfrac{0.60-0.80}{\sqrt{\frac{0.80 (1-0.80)}{50}}}=-3.536\)

Our \(z\) test statistic is -3.536.

3. Determine the p-value

This is a left-tailed test so we need to find the area to the right of our test statistic, \(z=-3.536\).

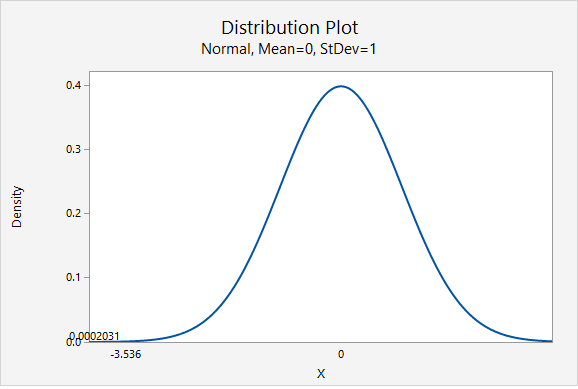
Distribution Plot of Density vs X - Normal, Mean=0, StDev=1

From the Minitab output above, the p-value is 0.0002031

4. Make a decision

\(p \leq.05\), therefore our decision is to reject the null hypothesis.

5. State a "real world" conclusion

Yes, there is convincing evidence that the percentage of all Creamery customers who prefer chocolate ice cream over vanilla is less than 80%.