8.2.2.1.2- Example: Sleep Deprivation
8.2.2.1.2- Example: Sleep DeprivationIn a class survey, students were asked how many hours they sleep per night. In the sample of 22 students, the mean was 5.77 hours with a standard deviation of 1.572 hours. That distribution was approximately normal. Let’s construct a 95% confidence interval for the mean number of hours slept per night in the population from which this sample was drawn.
This is what we know: \(n=22\), \(\overline{x}=5.77\), and \(s=1.572\).
In order to compute the confidence interval for \(\mu\) we will need the t multiplier and the standard error (\( \frac{s}{\sqrt{n}}\)).
\(df=n-1=22-1=21\)
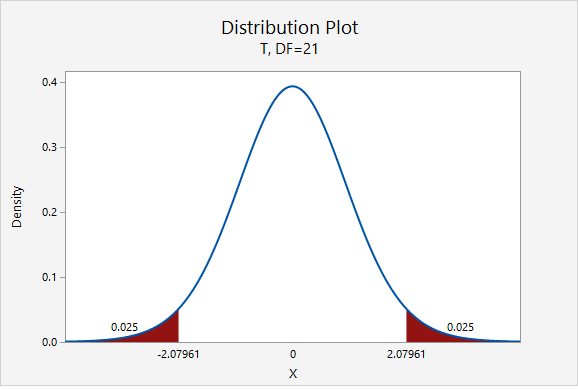
For a 95% confidence interval with 21 degrees of freedom, \(t^{*}=2.080\)
\(SE=\frac{s}{\sqrt{n}}=\frac{1.572}{\sqrt{22}}=0.335\)
Thus, our confidence interval for \(\mu\) is: \(5.77\pm 2.080(0.335)=5.77\pm0.697=[5.073,\;6.467]\)
We are 95% confident that the population mean is between 5.073 and 6.467 hours.
The only thing that would change is our multiplier. Now, \(t^{*}=2.831\).
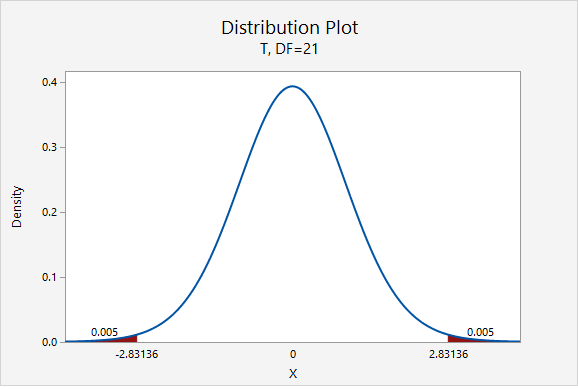
\(5.77\pm 2.831(0.335)=5.77\pm0.948=[4.822,\;6.718]\)
We are 99% confident that the population mean is between 4.822 and 6.718 hours.