9: Inference for Two Samples
9: Inference for Two SamplesObjectives
- Identify situations in which the z or t distribution may be used to approximate a sampling distribution
- Construct a confidence interval to estimate the difference in two population proportions and two population means using Minitab given summary or raw data
- Conduct a hypothesis test for two proportions and two means using Minitab given summary or raw data
Note: This lesson corresponds to Chapter 6: Sections 3 and 4 in the Lock5 textbook.
The general form of confidence intervals and test statistics will be the same for all of the procedures covered in this lesson:
- General Form of a Confidence Interval
- \(sample\ statistic\pm(multiplier)\ (standard\ error)\)
- General Form of a Test Statistic
- \(test\;statistic=\dfrac{sample\;statistic-null\;parameter}{standard\;error}\)
- Check assumptions and write hypotheses
The assumptions will vary depending on the test. The null and alternative hypotheses will also be written in terms of population parameters; the null hypothesis will always contain the equality (i.e., \(=\)). - Calculate the test statistic
This will vary depending on the test, but it will typically be the difference observed between the sample and population divided by a standard error. In this lesson we will see z and t test statistics. Minitab will compute the test statistic. - Determine the \(p\) value
This can be found using Minitab. - Make a decision
If \(p \leq \alpha\) reject the null hypothesis. If \(p>\alpha\) fail to reject the null hypothesis. - State a "real world" conclusion
Based on your decision in step 4, write a conclusion in terms of the original research question.
9.1 - Two Independent Proportions
9.1 - Two Independent ProportionsTwo independent proportions tests are used to compare the proportions in two unrelated groups. In StatKey these were known as "Difference in Proportions" tests.
Given that \(n_1 p_1 \ge 10\), \(n_1(1-p_1) \ge 10\), \(n_2 p_2 \ge 10\), and \(n_2(1-p_2) \ge 10\), where the subscript 1 represents the first group and the subscript 2 represents the second group, the sampling distribution will be approximately normal with a standard deviation (i.e., standard error) of \( \sqrt{\frac{p_1(1-p_1)}{n_1}+\frac{p_2(1-p_2)}{n_2}}\). Because the population proportions are not known, they are estimated using the sample proportions. This means if there are at least 10 "successes" and at least 10 "failures" in both groups the sampling distribution for the difference in proportions will be approximately normal.
If the assumption above is met, the normal approximation method is typically preferred. The normal approximation method uses the z distribution to approximate the sampling distribution, similar to the procedures we used in Lesson 7.
When this assumption is not met, Fisher's exact method, bootstrapping, or randomization methods may be used. Fisher's exact method will not be covered in this course. Bootstrapping and randomization methods were covered in Lessons 4 and 5, respectively.
9.1.1 - Confidence Intervals
9.1.1 - Confidence IntervalsGiven that \(np \ge 10\) and \(n(1-p) \ge 10\) for both groups, in other words at least 10 "successes" and at least 10 "failures" in each group, the sampling distribution can be approximated using the normal distribution with a mean of \(\widehat p_1 - \widehat p_2\) and a standard error of \(\sqrt{\frac{p_1(1-p_1)}{n_1}+\frac{p_2(1-p_2)}{n_2}}\).
Recall from the general form of a confidence interval:
- General Form of a Confidence Interval
- \(sample\ statistic\pm(multiplier)\ (standard\ error)\)
Here, the sample statistic is the difference between the two proportions (\(\widehat p_1 - \widehat p_2\)) and the standard error is computed using the formula \(\sqrt{\frac{p_1(1-p_1)}{n_1}+\frac{p_2(1-p_2)}{n_2}}\). Putting this information together, we can derive the formula for a confidence interval for the difference between two proportions.
- Confidence Interval for the Difference Between Two Proportions
- \((\widehat{p}_1-\widehat{p}_2) \pm z^\ast {\sqrt{\dfrac{\widehat{p}_1 (1-\widehat{p}_1)}{n_1}+\dfrac{\widehat{p}_2 (1-\widehat{p}_2)}{n_2}}}\)
Example: Confidence Interval for the Difference Between the Proportion of Women and Men in Favor of Legal Same Sex Marriage
A survey was given to a sample of college students. They were asked whether they think same sex marriage should be legal. Of the 251 women in the sample, 185 said "yes." Of the 199 men in the sample, 107 said "yes." Let’s construct a 95% confidence interval for the difference of the proportion of women and men who responded “yes.” We can apply the 95% Rule and use a multiplier of \(z^\ast\) = 2
- For women: \(np=185\) and \(n(1-p) = 251-185=66\)
- For men: \(np=107\) and \(n(1-p)=199-107=92\)
These counts are all at least 10 so the sampling distribution can be approximated using a normal distribution.
\(\widehat{p}_{w}=\frac{185}{251}=0.737\)
\(\widehat{p}_{m}=\frac{107}{199}=0.538\)
\((0.737-0.538) \pm 2 {\sqrt{\dfrac{0.737 (1-0.737)}{251}+\dfrac{0.538 (1-0.538)}{199}}}\)
\(0.199 \pm 2 ( 0.045)\)
\(.199 \pm .090=[.110, .288]\)
We are 95% confident that in the population the difference between the proportion of women and men who are in favor of same sex marriage legalization is between 0.110 and 0.288.
This confidence interval does not contain 0. Therefore it is not likely that the difference between women and men is 0. We can conclude that there is a difference between the proportion of women and men in the population who would respond “yes" to this question.
9.1.1.1 - Minitab: Confidence Interval for 2 Proportions
9.1.1.1 - Minitab: Confidence Interval for 2 ProportionsMinitab can be used to construct a confidence interval for the difference between two proportions using the normal approximation method. Note that the confidence intervals given in the Minitab output assume that \(np \ge 10\) and \(n(1-p) \ge 10\) for both groups. If this assumption is not true, you should use bootstrapping methods in StatKey.
Minitab® – Constructing a Confidence Interval with Raw Data
Let's estimate the difference between the proportion of females who have tried weed and the proportion of males who have tried weed.
- Open Minitab file: class_survey.mpx
- Select Stat > Basic Statistics > 2 Proportions
- Select Both samples are in one column from the dropdown
- Double click the variable Try Weed in the Samples box
- Double click the variable Biological Sex in the Sample IDs box
- Keep the default Options
- Click OK
This should result in the following output:
Method
Event: Try_Wee = Yes
\(p_1\): proportion where Try_Weed = Yes and Biological Sex = Female
\(p_2\): proportion where Try-Weed = Yes and Biological Sex = Male
Difference: \(p_1\)-\(p_2\)
Descriptive Statistics: Try Weed
| Biological Sex | N | Event | Sample p |
|---|---|---|---|
| Female | 127 | 56 | 0.440945 |
| Male | 99 | 62 | 0.626263 |
Estimation for Difference
| Difference | 95% CI for Difference |
|---|---|
| -0.185318 | (-0.313920, -0.056716) |
CI based on normal approximation
Test
| Null hypothesis | \(H_0\): \(p_1-p_2=0\) |
|---|---|
| Alternative hypothesis | \(H_1\): \(p_1-p_2\neq0\) |
| Method | Z-Value | P-Value |
|---|---|---|
| Normal approximation | -2.82 | 0.005 |
| Fisher's exact | 0.007 |
Minitab® – Constructing a Confidence Interval with Summarized Data
Let's estimate the difference between the proportion of Penn State World Campus graduate students who have children to the proportion of Penn State University Park graduate students who have children. In our representative sample there were 120 World Campus graduate students; 92 had children. There were 160 University Park graduate students; 23 had children.
- Open Minitab
- Select Stat > Basic Statistics > Two-Sample Proportion
- Select Summarized data in the dropdown
- For Sample 1 next to Number of events enter 92 and next to Number of trials enter 120
- For Sample 2 next to Number of events enter 23 and next to Number of trials enter 160
- Keep the default Options
- Click OK
This should result in the following output:
Method
\(p_1\): proportion where Sample 1 = Event
\(p_2\): proportion where Sample 2 = Event
Difference: \(p_1\)-\(p_2\)
Descriptive Statistics
| Sample | N | Event | Sample p |
|---|---|---|---|
| Sample 1 | 120 | 92 | 0.766667 |
| Sample 2 | 160 | 23 | 0.143750 |
Estimation for Difference
| Difference | 95% CI for Difference |
|---|---|
| 0.622917 | (0.529740, 0.716093) |
CI based on normal approximation
| Null hypothesis | \(H_0\): \(p_1-p_2=0\) |
|---|---|
| Alternative hypothesis | \(H_1\): \(p_1-p_2\neq0\) |
| Method | Z-Value | P-Value |
|---|---|---|
| Normal approximation | 13.10 | 0.000 |
| Fisher's exact | 0.000 |
9.1.2 - Hypothesis Testing
9.1.2 - Hypothesis TestingHere we will walk through the five-step hypothesis testing procedure for comparing the proportions from two independent groups. In order to use the normal approximation method there must be at least 10 "successes" and at least 10 "failures" in each group. In other words, \(n p \geq 10\) and \(n (1-p) \geq 10\) for both groups.
If this assumption is not met you should use Fisher's exact method in Minitab or bootstrapping methods in StatKey.
9.1.2.1 - Normal Approximation Method Formulas
9.1.2.1 - Normal Approximation Method Formulas1. Check any necessary assumptions and write null and alternative hypotheses.
To use the normal approximation method a minimum of 10 successes and 10 failures in each group are necessary (i.e., \(n p \geq 10\) and \(n (1-p) \geq 10\)).
The two groups that are being compared must be unpaired and unrelated (i.e., independent).
Below are the possible null and alternative hypothesis pairs:
| Research Question | Are the proportions of group 1 and group 2 different? | Is the proportion of group 1 greater than the proportion of group 2? | Is the proportion of group 1 less than the proportion of group 2? |
|---|---|---|---|
| Null Hypothesis, \(H_{0}\) | \(p_1 - p_2=0\) | \(p_1 - p_2=0\) | \(p_1 - p_2=0\) |
| Alternative Hypothesis, \(H_{a}\) | \(p_1 - p_2 \neq 0\) | \(p_1 - p_2> 0\) | \(p_1 - p_2<0\) |
| Type of Hypothesis Test | Two-tailed, non-directional | Right-tailed, directional | Left-tailed, directional |
The null hypothesis is that there is not a difference between the two proportions (i.e., \(p_1 = p_2\)). If the null hypothesis is true then the population proportions are equal. When computing the standard error for the difference between the two proportions a pooled proportion is used as opposed to the two proportions separately (i.e., unpooled). This pooled estimate will be symbolized by \(\widehat{p}\). This is similar to a weighted mean, but with two proportions.
- Pooled Estimate of \(p\)
- \(\widehat{p}=\dfrac{\widehat{p}_1n_1+\widehat{p}_2n_2}{n_1+n_2}\)
The standard error for the difference between two proportions is symbolized by \(SE_{0}\). The subscript 0 tells us that this standard error is computed under the null hypothesis (\(H_0: p_1-p_2=0\)).
- Standard Error
-
\(SE_0={\sqrt{\dfrac{\widehat{p} (1-\widehat{p})}{n_1}+\dfrac{\widehat{p}(1-\widehat{p})}{n_2}}}=\sqrt{\widehat{p}(1-\widehat{p})\left ( \dfrac{1}{n_1}+\dfrac{1}{n_2} \right )}\)
Note that the default in many statistical programs, including Minitab, is to estimate the two proportions separately (i.e., unpooled). In order to obtain results using the pooled estimate of the proportion you will need to change the method.
Also note that this standard error is different from the one that you used when constructing a confidence interval for \(p_1-p_2\). While the hypothesis testing procedure is based on the null hypothesis that \(p_1-p_2=0\), the confidence interval approach is not based on this premise. The hypothesis testing approach uses the pooled estimate of \(p\) while the confidence interval approach will use an unpooled method.
- Test Statistic for Two Independent Proportions
- \(z=\dfrac{\widehat{p}_1-\widehat{p}_2}{SE_0}\)
The \(z\) test statistic found in Step 2 is used to determine the \(p\) value. The \(p\) value is the proportion of the \(z\) distribution (normal distribution with a mean of 0 and standard deviation of 1) that is more extreme than the test statistic in the direction of the alternative hypothesis.
If \(p \leq \alpha\) reject the null hypothesis. If \(p>\alpha\) fail to reject the null hypothesis.
Based on your decision in Step 4, write a conclusion in terms of the original research question.
9.1.2.1.1 – Example: Ice Cream
9.1.2.1.1 – Example: Ice CreamExample: Ice Cream
The Creamery wants to compare adults and children in terms of preference for eating their ice cream out of a cone. They take a representative sample of 500 customers (240 adults and 260 children) and ask if they prefer cones over bowls. They found that 124 adults preferred cones and 90 children preferred cones.
\(H_0: p_a - p_c = 0\)
\(H_a:p_a - p_c \ne 0\)
Check assumptions:
\(n_a \hat{p}_a = 124\)
\(n_a (1-\widehat p_a) = 240 - 124 = 116\)
\(n_c \widehat p_c = 90\)
\(n_c (1-\widehat p_c) = 260-90 = 170\)
These counts are all at least 10 so we can use the normal approximation method.
Pooled Estimate of \(p\)
\(\widehat{p}=\dfrac{\widehat{p}_1n_1+\widehat{p}_2n_2}{n_1+n_2}\)
\(\widehat{p}=\dfrac{124+90}{240+260}=\dfrac{214}{500}=0.428\)
Standard Error of \(\hat{p}\)
\(SE_{0}={\sqrt{\frac{\widehat{p} (1-\widehat{p})}{n_1}+\frac{\widehat{p}(1-\widehat{p})}{n_2}}}=\sqrt{\widehat{p}(1-\widehat{p})\left ( \frac{1}{n_1}+\frac{1}{n_2} \right )}\)
\(SE_{0}=\sqrt{0.428(1-0.428)\left ( \dfrac{1}{240}+\dfrac{1}{260} \right )}=0.04429\)
Test Statistic for Two Independent Proportions
\(z=\dfrac{\widehat{p}_1-\widehat{p}_2}{SE_0}\)
\(z=\dfrac{\dfrac{124}{240}-\dfrac{90}{260}}{0.04429}=3.850\)
This is a two-tailed test. Our p-value will be the area of the \(z\) distribution more extreme than \(3.850\).
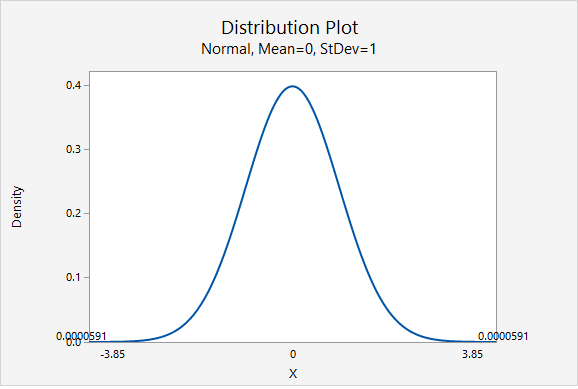
\(p = 0.0000591 \times 2 = 0.0001182\)
\(p \le 0.05\)
Reject the null hypothesis
There is convincing evidence that, in the population of Creamery customers, the proportion of adults who prefer cones is different from the proportion of children who prefer cones in the population.
9.1.2.1.2 – Example: Same Sex Marriage
9.1.2.1.2 – Example: Same Sex MarriageExample: Same Sex Marriage
A survey was given to a random sample of college students. They were asked whether they think same sex marriage should be legal. We're going to compare the students who identified as women and men in terms of whether or not they responded "yes" to this question. Of the 251 women in the sample, 185 said "yes." Of the 199 men in the sample, 107 said "yes."
For women, there were 185 who said "yes" and 66 who said "no." For men, there were 107 who said "yes" and 92 who said "no." There are at least 10 successes and failures in each group so the normal approximation method can be used.
\(\widehat{p}_{w}=\dfrac{185}{251}\)
\(\widehat{p}_{m}=\dfrac{107}{199}\)
This is a two-tailed test because we are looking for a difference between women and men, we were not given a specific direction.
- \( H_{0} : p_{w}- p_{m}=0 \)
- \( H_{a} : p_{w}- p_{m}\neq 0 \)
\(\widehat{p}=\dfrac{185+107}{251+199}=\dfrac{292}{450}=0.6489\)
\(SE_0=\sqrt{\frac{292}{450}\left ( 1-\frac{292}{450} \right )\left ( \frac{1}{251}+\frac{1}{199} \right )}=0.0453\)
\(z=\dfrac{\frac{185}{251}-\frac{107}{199}}{0.0453}=4.400\)
Our test statistic is \(z=4.400\)
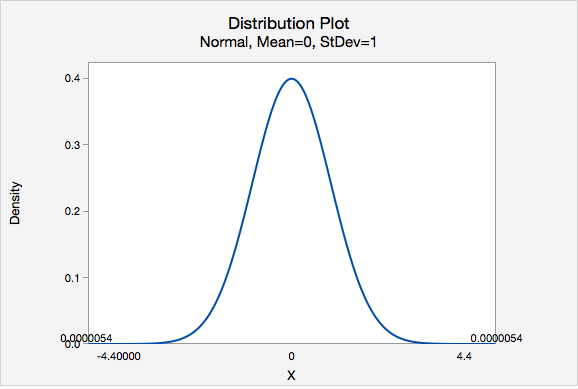
\(P(z>4.400)=0.0000054\), this is a two-tailed test, so this value must be multiplied by two: \(0.0000054\times 2= 0.0000108\)
\(p<0.0001\)
\(p\leq0.05\), therefore we reject the null hypothesis.
There is convincing evidence, in this population of students, that there is a difference between the proportion of women and men who think that same sex marriage should be legal.
9.1.2.2 - Minitab: Difference Between 2 Independent Proportions
9.1.2.2 - Minitab: Difference Between 2 Independent ProportionsWhen conducting a hypothesis test comparing the proportions of two independent proportions in Minitab two p-values are provided. If \(np \ge 10\) and \(n(1-p) \ge 10\), use the p-value associated with the normal approximation method. If this assumption is not met, use the p-value associated with Fisher's exact method.
Minitab Note!
When conducting a hypothesis test for a difference between two independent proportions in Minitab you need to remember to change the "test method" to "use the pooled estimate of the proportion." This is because the null hypothesis is that the two proportions are equal.
Minitab® – Testing Two Independent Proportions using Raw Data
Let's compare the proportion of females who have tried weed to the proportion of males who have tried weed.
- Open Minitab file: class_survey.mpx
- Select Stat > Basic Statistics > 2 Proportions
- Select Both samples are in one column from the dropdown
- Double click the variable Try Weed in the box on the left to insert the variable into the Samples box
- Double click the variable Biological Sex in the box on the left to insert the variable into the Sample IDs box
- Under the Options tab change the Test method to Use the pooled estimate of the proportion
- Click OK and OK
This should result in the following output:
Method
Event: Try_Weed = Yes
\(p_1\): proportion where Try_Weed = Yes and Biological Sex = Female
\(p_2\): proportion where Try-Weed = Yes and Biological Sex = Male
Difference: \(p_1\)-\(p_2\)
Descriptive Statistics: Try Weed
Biological Sex | N | Event | Sample p |
|---|---|---|---|
Female | 127 | 56 | 0.440945 |
Male | 99 | 62 | 0.626263 |
Estimation for Difference
Difference | 95% CI for Difference |
|---|---|
-0.185318 | (-0.313920, -0.056716) |
CI based on normal approximation
Test
Null hypothesis | \(H_0\): \(p_1-p_2=0\) |
|---|---|
Alternative hypothesis | \(H_1\): \(p_1-p_2\neq0\) |
Method | Z-Value | P-Value |
|---|---|---|
Normal approximation | -2.77 | 0.006 |
Fisher's exact | 0.007 |
The test based on the normal approximation uses the pooled estimate of the proportion (0.522124)
Five Step Hypothesis Testing Procedure: Weed Example
Step 1:
\(H_0 : p_f - p_m =0\)
\(H_a : p_f - p_m \neq 0\)
Check assumptions:
\(n_f p_f = 56\)
\(n_f (1-p_f) = 127-56 = 71\)
\(n_m p_m = 62\)
\(n_m (1-p_m) = 99-62 = 37\)
All \(np\) and \(n(1-p)\) are at least ten, therefore we can use the normal approximation method.
Step 2:
From output, \(z=-2.77\)
Step 3:
From output, \(p=0.006\)
Step 4:
\(p \leq \alpha\), reject the null hypothesis
Step 5:
There is convincing evidence that in the population the proportion of females who have tried weed is different from the proportion of males who have tried weed.
Minitab® – Testing Two Independent Proportions using Summarized Data
Let's compare the proportion of Penn State World Campus graduate students who have children to the proportion of Penn State University Park graduate students who have children. In a representative sample there were 120 World Campus graduate students; 92 had children. There were 160 University Park graduate students; 23 had children.
- In Minitab, select Stat > Basic Statistics > 2 Proportions
- Change Both samples are in one column to Summarized data in the dropdown
- For Sample 1 next to Number of events enter 92 and next to Number of trials enter 120
- For Sample 2 next to Number of events enter 23 and next to Number of trials enter 160
- Under the Options tab change the Test method to Use the pooled estimate of the proportion
- Click OK and OK
This should result in the following output:
Method
\(p_1\): proportion where Sample 1 = Event
\(p_2\): proportion where Sample 2 = Event
Difference: \(p_1\)-\(p_2\)
Descriptive Statistics
Sample | N | Event | Sample p |
|---|---|---|---|
Sample 1 | 120 | 92 | 0.766667 |
Sample 2 | 160 | 23 | 0.143750 |
Estimation for Difference
Difference | 95% CI for Difference |
|---|---|
0.622917 | (0.529740, 0.716093) |
CI based on normal approximation
Test
Null hypothesis | \(H_0\): \(p_1-p_2=0\) |
|---|---|
Alternative hypothesis | \(H_1\): \(p_1-p_2\neq0\) |
Method | Z-Value | P-Value |
|---|---|---|
Normal approximation | 10.49 | 0.000 |
Fisher's exact | 0.000 |
The test based on the normal approximation uses the pooled estimate of the proportion (0.410714)
Five Step Hypothesis Testing Procedure: Parents
Step 1:
\(H_0 : p_w - p_u =0\)
\(H_a : p_w - p_u \neq 0\)
Check assumptions:
\(n_w p_w = 92\)
\(n_w (1-p_w) = 120-92 = 28\)
\(n_u p_u = 23\)
\(n_u (1-p_u) = 160-23 = 137\)
All \(np\) and \(n(1-p)\) are at least ten, therefore we can use the normal approximation method.
Step 2:
From output, \(z=10.49\)
Step 3:
From output, \(p=0.000\)
Step 4:
\(p \leq \alpha\), reject the null hypothesis
Step 5:
There is convincing evidence that in the population the proportion of World Campus students who have children is different from the proportion of University Park students who have children.
9.1.2.2.1 - Example: Dating
9.1.2.2.1 - Example: DatingExample: Dating
This example uses the course survey dataset:
A random sample of Penn State University Park undergraduate students were asked, "Would you date someone with a great personality even if you did not find them attractive?" Let's compare the proportion of males and females who responded "yes" to determine if there is convincing evidence of a difference.
We are looking for a "difference," so this is a two-tailed test.
\(H_{0} \colon p_1 - p_2 =0\)
\( H_{a} \colon p_1 - p_2 \neq 0 \)
Check assumptions
\(n_f p_f = 367\)
\(n_f (1-p_f) = 571 - 367 = 204\)
\(n_m p_m = 148\)
\(n_m (1 - p_m) = 433 - 148 = 285\)
All of these counts are at least 10 so we will use the normal approximation method.
From output, \(z=9.45\)
Event: DatePerly = Yes |
\(p_1\): proportion where DatePerly = Yes and Gender = Female |
\(p_2\): proportion where DatePerly = Yes and Gender = Male |
Difference: \(p_1-p_2\) |
Gender | N | Event | Sample p |
|---|---|---|---|
Female | 571 | 367 | 0.642732 |
Male | 433 | 148 | 0.341801 |
Difference | 95% CI for Difference |
|---|---|
0.300931 | (0.241427, 0.360435) |
Null hypothesis | \(H_0\): \(p_1-p_2=0\) |
|---|---|
Alternative hypothesis | \(H_1\): \(p_1-p_2\neq0\) |
Method | Z-Value | P-Value |
|---|---|---|
Fisher's exact | <0.0001 | |
Normal approximation | 9.45 | <0.0001 |
The pooled estimate of the proportion (0.512948) is used for the tests.
From output, \(p<0.0001\)
\(p \leq \alpha\), reject the null hypothesis
There is convincing evidence that in the population of all Penn State University Park undergraduate students the proportion of men who would date someone with a great personality even if they did not find them attractive is different from the proportion of women who would date someone with a great personality even if they did not find them attractive.
9.2 - Two Independent Means
9.2 - Two Independent MeansLet's explore how we can compare the means of two independent groups. If the populations are known to be approximately normally distributed, or if both sample sizes are at least 30, then the sampling distribution can be estimated using the \(t\) distribution. If this assumption is not met then simulation methods (i.e., bootstrapping or randomization) may be used.
9.2.1 - Confidence Intervals
9.2.1 - Confidence IntervalsGiven that the populations are known to be normally distributed, or if both sample sizes are at least 30, then the sampling distribution can be approximated using the \(t\) distribution, and the formulas below may be used. Here you will be introduced to the formulas to construct a confidence interval using the \(t\) distribution. Minitab will do all of these calculations for you, however, it uses a more sophisticated method to compute the degrees of freedom so answers may vary slightly, particularly with smaller sample sizes.
- General Form of a Confidence Interval
- \(point \;estimate \pm (multiplier) (standard \;error)\)
Here, the point estimate is the difference between the two mean, \(\bar{x} _1 - \bar{x}_2\).
- Standard Error
- \(\sqrt{\dfrac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}\)
- Confidence Interval for Two Independent Means
- \((\bar{x}_1-\bar{x}_2) \pm t^\ast{ \sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}}\)
The degrees of freedom can be approximated as the smallest sample size minus one.
- Estimated Degrees of Freedom
-
\(df=smallest\;n-1\)
Example: Exam Scores by Learner Type
A STAT 200 instructor wants to know how traditional students and adult learners differ in terms of their final exam scores. She collected the following data from a sample of students:
| Traditional Students | Adult Learners | |
|
\(\overline x\) |
41.48 | 40.79 |
| \(s\) | 6.03 | 6.79 |
| \(n\) | 239 | 138 |
She wants to construct a 95% confidence interval to estimate the mean difference.
The point estimate, or "best estimate," is the difference in sample means:
\(\overline x _1 - \overline x_2 = 41.48-40.79=0.69\)
The standard error can be computed next:
\(\sqrt{\dfrac{s_1^2}{n_1}+\dfrac{s_2^2}{n_2}}=\sqrt{\dfrac{6.03^2}{239}+\dfrac{6.79^2}{138}}=0.697\)
To find the multiplier, we need to construct a t distribution with \(df=smaller\;n-1=138-1=137\) to find the t scores that separate the middle 95% of the distribution from the outer 5% of the distribution:
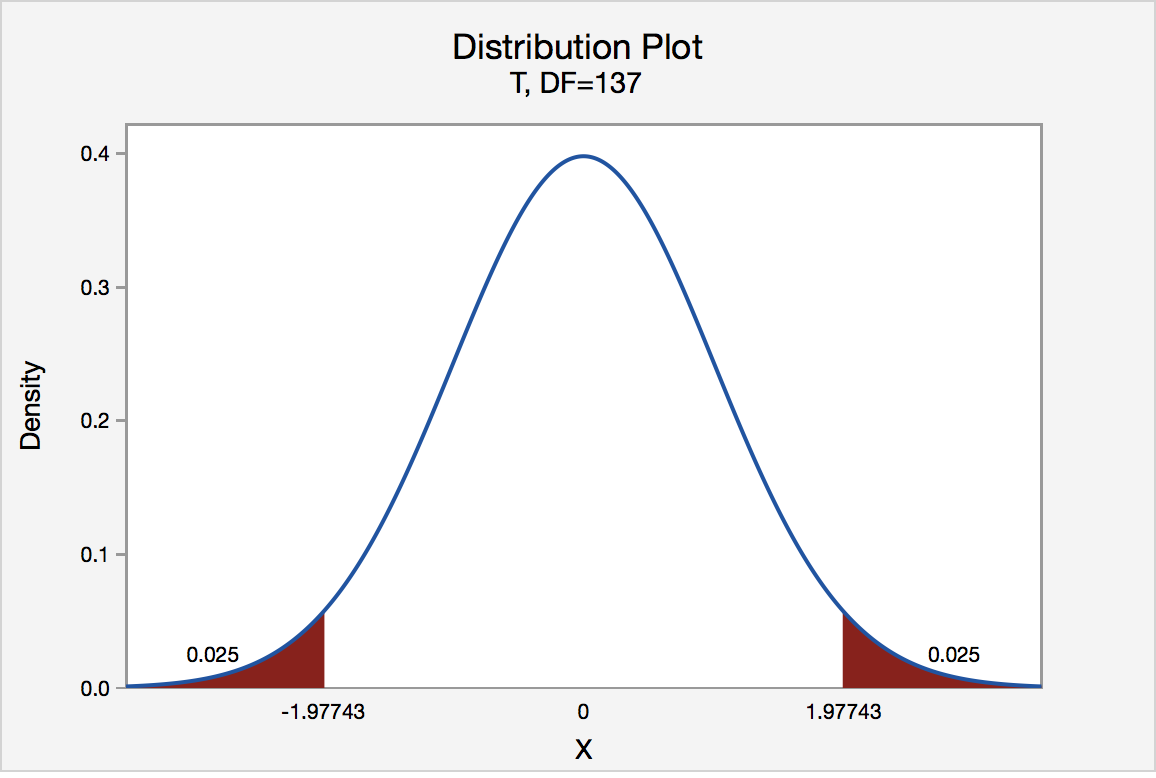
\(t^*=1.97743\)
Now, we can combine all of these values to construct our confidence interval:
\(point \;estimate \pm (multiplier) (standard \;error)\)
\(0.69 \pm 1.97743 (0.697)\)
\(0.69 \pm 1.379\) The margin of error is 1.379
\([-0.689, 2.069]\)
We are 95% confident that the mean difference in traditional students' and adult learners' final exam scores is between -0.689 points and +2.069 points.
9.2.1.1 - Minitab: Confidence Interval Between 2 Independent Means
9.2.1.1 - Minitab: Confidence Interval Between 2 Independent MeansMinitab can be used to construct a confidence interval for the difference between two independent means. Note that the confidence intervals given in the Minitab output assume that either the populations are normally distributed or that both sample sizes are at least 30.
Minitab® – Confidence Interval Between 2 Independent Means
Let's estimate the difference between the mean weight (in pounds) of females and the mean weight of males. Both sample sizes are at least 30 so the sampling distribution can be approximated using the t distribution.
- Open the Minitab file: class_survey.mpx
- Select Stat > Basic Statistics > 2 Sample t
- Select Both samples are in one column from the dropdown
- Double click the variable Weight in the box on the left to insert the variable into the Samples box
- Double click the variable Biological Sex in the box on the left to insert the variable into the Sample IDs box
- Click OK
This should result in the following output:
Method
\(\mu_1\): mean of Weight when Biological Sex = Female
\(\mu_2\): mean of Weight when Biological Sex = Male
Difference: \(\mu_1-\mu_2\)
Equal variances are not assumed for this analysis.
Descriptive Statistics: Weight
| Gender | N | Mean | StDev | SE Mean |
|---|---|---|---|---|
| Female | 126 | 136.7 | 23.4 | 2.1 |
| Male | 99 | 172.7 | 27.3 | 2.7 |
Estimation for Difference
| Difference | 95% CI for Difference |
|---|---|
| -35.99 | (-42.79, -29.20) |
Interpret
I am 95% confident that in the population the mean weight of females is between 29.202 pounds and 42.787 pounds less than the mean weight of males.
9.2.1.1.1 - Video Example: Mean Difference in Exam Scores, Summarized Data
9.2.1.1.1 - Video Example: Mean Difference in Exam Scores, Summarized Data9.2.2 - Hypothesis Testing
9.2.2 - Hypothesis TestingThe formula for the test statistic follows the same general format as the others that we have seen this week:
- Test Statistic
- \(test\; statistic = \dfrac{sample \; statistic - null\;parameter}{standard \;error}\)
Minitab will compute the test statistic for you! You will just need to determine if equal variances should be assumed or not. There is one example below walking through these procedures by hand, but you are strongly encouraged to use Minitab whenever possible.
There are two assumptions: (1) the two samples are independent and (2) both populations are normally distributed or \(n_1 \geq 30\) and \(n_2 \geq 30\). If the second assumption is not met then you can conduct a randomization test.
Below are the possible null and alternative hypothesis pairs:
| Research Question | Are the means of group 1 and group 2 different? | Is the mean of group 1 greater than the mean of group 2? | Is the mean of group 1 less than the mean of group 2? |
|---|---|---|---|
| Null Hypothesis, \(H_{0}\) | \(\mu_1 = \mu_2\) | \(\mu_1 = \mu_2\) | \(\mu_1 = \mu_2\) |
| Alternative Hypothesis, \(H_{a}\) | \(\mu_1 \neq \mu_2\) | \(\mu_1 > \mu_2\) | \(\mu_1 < \mu_2\) |
| Type of Hypothesis Test | Two-tailed, non-directional | Right-tailed, directional | Left-tailed, directional |
Standard Error
\(\sqrt{\dfrac{s_1^2}{n_1}+\dfrac{s_2^2}{n_2}}\)
Test Statistic for Independent Means
\(t=\dfrac{\bar{x}_1-\bar{x}_2}{ \sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}}\)
Estimated Degrees of Freedom
\(df=smallest\;n - 1\)
The \(t\) test statistic found in Step 2 is used to determine the p-value.
If \(p \leq \alpha\) reject the null hypothesis. If \(p>\alpha\) fail to reject the null hypothesis.
Based on your decision in Step 4, write a conclusion in terms of the original research question.
9.2.2.1 - Minitab: Independent Means t Test
9.2.2.1 - Minitab: Independent Means t TestHere we will use Minitab to conduct an independent means t-test. Note that Minitab uses a more complicated formula for computing the degrees of freedom for this test.
Within Minitab, the procedure for obtaining the test statistic and confidence interval for independent means is identical.
Minitab® – Conducting an Independent Means t Test
Let's compare the mean SAT-Math scores of students who have and have not ever cheated. Both sample sizes are at least 30 so the sampling distribution can be approximated using the \(t\) distribution.
- Open the Minitab file: class_survey.mpx
- Select Stat > Basic Statistics > 2 Sample t...
- Enter the variable SATM into the Samples box
- Enter variable Ever_Cheat into the Sample IDs box
- Click OK
This should result in the following output:
Method
\(\mu_1\): mean of SATM when Ever_Cheat = No
\(\mu_2\): mean of SATM when Ever_Cheat = Yes
Difference: \(\mu_1-\mu_2\)
Equal variances are not assumed for this analysis.
Descriptive Statistics: SATM
| Ever_Cheat | N | Mean | StDev | SE Mean |
|---|---|---|---|---|
| No | 163 | 604.0 | 86.9 | 6.8 |
| Yes | 53 | 583.7 | 79.2 | 11 |
Estimation of Difference
| Difference | 95% CI for Difference |
|---|---|
| 20.3 | (-5.2, 45.8) |
Test
| Null hypothesis | \(H_0\): \(\mu_1-\mu_2=0\) |
|---|---|
| Alternative hypothesis | \(H_1\): \(\mu_1-\mu_2\neq0\) |
| T-Value | DF | P-Value |
|---|---|---|
| 1.58 | 95 | 0.117 |
The result of our two independent means t test is \(t(95) = 1.58, p = 0.117\). Our p-value is greater than the standard alpha level of 0.05 so we fail to reject the null hypothesis. There is not enough evidence to state that the mean SAT-Math scores of students who have and have not ever cheated are different.
Note that we could also interpret the confidence interval in this output. We are 95% confident that the mean difference in the population is between -5.16 and 45.78.
The example above uses a dataset. The following examples show how you can conduct this type of test using summarized data.
9.2.2.1.1 - Example: Summarized Data
9.2.2.1.1 - Example: Summarized DataExample: Weight by Treatment
Research question: Do patients who receive our treatment weigh less than participants who do not receive our treatment?
Participants were randomly assigned to the treatment condition or a control group. After our intervention, their weights were measured in pounds. Weight is a quantitative variable, so we are going to be comparing means in this example. If assumptions are met, we’ll be conducting a two independent means t test.
Our treatment group has a sample size of 45, mean of 140 pounds, and standard deviation of 20 pounds. Our control group has a sample size of 40, sample mean of 150 pounds, and standard deviation of 25 pounds.
Follow the 5 step hypothesis testing procedure to analyze this data in Minitab.
There are two assumptions: (1) the two samples are independent and (2) both populations are normally distributed or \(n_1 \geq 30\) and \(n_2 \geq 30\). The participants were randomly assigned to one of the two groups. They are in no way matched or paired so they are independent. Both groups have sample size of at least 30.
Our hypotheses is based on the research question "Do patients who receive our treatment weigh less than participants who do not receive our treatment?." This indicates a left tail test. (T = treatment group, C = control group)
\(H_0\): \(\mu_T = \mu_C\)
\(H_a\): \(\mu_T < \mu_C\)
Use Minitab to perform the t-test.
2-Sample independent t-test using summarized data
- Open Minitab
- Select Stat > Basic Statistics > 2 Sample t...
- Select Summarized data in the dropdown at the top
- Enter the summary statistics in the table with the treatment group as Sample 1 and the control group as Sample 2.
Sample 1 | Sample 2 | |
|---|---|---|
Sample size: | 45 | 40 |
Sample means: | 140 | 150 |
Standard deviation: | 20 | 25 |
- Select the Options button
- For the Alternative hypothesis choose Difference < hypothesized difference
- OK and OK
And we get the following output:
Method
\(\mu_1\): population mean of Sample 1
\(\mu_2\): population mean of Sample 2
Difference: \(\mu_1-\mu_2\)
Equal variances are not assumed for this analysis.
Descriptive Statistics
Sample | N | Mean | StDev | SE Mean |
|---|---|---|---|---|
Sample 1 | 45 | 140.0 | 20.0 | 3.0 |
Sample 2 | 40 | 150.0 | 25.0 | 4.0 |
Estimation of Difference
Difference | 95% CI for Difference |
|---|---|
-10.00 | -1.75 |
Test
Null hypothesis | \(H_0\): \(\mu_1-\mu_2=0\) |
|---|---|
Alternative hypothesis | \(H_1\): \(\mu_1-\mu_2\lt0\) |
T-Value | DF | P-Value |
|---|---|---|
-2.02 | 74 | 0.024 |
The t-value is -2.02.
The p-value is 0.024.
\(p \leq \alpha\), reject the null hypothesis.
There is convincing evidence that patients who receive our treatment weigh less than participants who do not receive our treatment in the population.
9.2.2.1.3 - Example: Height by Sex
9.2.2.1.3 - Example: Height by SexResearch Question: In the population of all college students, is the mean height of females less than the mean height of males?
Data concerning height (in inches) were collected from 99 females and 126 males.
This example uses the following Minitab file: class_survey.csv
We have two independent groups: females and males. Height in inches is a quantitative variable. This means that we will be comparing the means of two independent groups.
There are 126 females and 99 males in our sample. The sampling distribution will be approximately normally distributed because both sample sizes are at least 30.
This is a left-tailed test because we want to know if the mean for females is less than the mean for males.
(Note: Minitab will arrange the levels of the explanatory variable in alphabetical order. This is why "females" are listed before "males" in this example.)
\(H_{0}:\mu_f = \mu_m \)
\(H_{a}: \mu_f < \mu_m \)
- Open the file and select Stat > Basic Statistics > 2 Sample t...
- Enter variable Height into the Samples box
- Enter the variable Biological Sex in the box into the Sample IDs box
- Choose Options and select 'Difference < Hypothesized difference' for the alternative hypothesis.
- Click OK
This should result in the following output:
Method
\(\mu_1\): mean of Height when Biological Sex = Female
\(\mu_2\): mean of Height when Biological Sex = Male
Difference: \(\mu_1-\mu_2\)
Equal variances are not assumed for this analysis.
Descriptive Statistics: Height
Gender | N | Mean | StDev | SE Mean |
|---|---|---|---|---|
Female | 126 | 65.62 | 6.53 | 0.58 |
Male | 99 | 70.24 | 3.63 | 0.37 |
Estimation for Difference
Difference | 95% Upper Bound for Difference |
|---|---|
-4.623 | -3.488 |
Test
Null hypothesis | \(H_0\): \(\mu_1-\mu_2=0\) |
|---|---|
Alternative hypothesis | \(H_1\): \(\mu_1-\mu_2<0\) |
T-Value | DF | P-Value |
|---|---|---|
-6.73 | 202 | 0.000 |
The test statistic is t = -6.73
From the output given in Step 2, the p-value is 0.000
\(p\leq.05\), therefore we reject the null hypothesis.
There is convincing evidence that the mean height of female students is less than the mean height of male students in the population.
9.3 - Lesson 9 Summary
9.3 - Lesson 9 SummaryObjectives
- Identify situations in which the z or t distribution may be used to approximate a sampling distribution
- Construct a confidence interval to estimate the difference in two population proportions and two population means using Minitab given summary or raw data
- Conduct a hypothesis test for two proportions and two means using Minitab given summary or raw data
| Confidence Interval | Test Statistic | |
|---|---|---|
| Two Independent Proportions At least 10 successes and 10 failures in both samples. |
\((\widehat{p}_1-\widehat{p}_2) \pm z^\ast {\sqrt{\dfrac{\widehat{p}_1 (1-\widehat{p}_1)}{n_1}+\dfrac{\widehat{p}_2 (1-\widehat{p}_2)}{n_2}}}\) | \(z=\dfrac{\widehat{p}_1-\widehat{p}_2}{\sqrt{\widehat{p}(1-\widehat{p})\left ( \dfrac{1}{n_1}+\dfrac{1}{n_2} \right )}}\) |
| Two Independent Means Both sample size are at least 30 OR populations are normally distributed. |
\((\bar{x}_1-\bar{x}_2) \pm t^\ast{ \sqrt{\dfrac{s_1^2}{n_1}+\dfrac{s_2^2}{n_2}}}\) \(Estimated \;df = smallest\; n - 1\) |
\(t=\dfrac{\bar{x}_1-\bar{x}_2}{ \sqrt{\dfrac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}}\) \(Estimated \;df = smallest\; n - 1\) |