9.1.2.1 - Normal Approximation Method Formulas
9.1.2.1 - Normal Approximation Method Formulas1. Check any necessary assumptions and write null and alternative hypotheses.
To use the normal approximation method a minimum of 10 successes and 10 failures in each group are necessary (i.e., \(n p \geq 10\) and \(n (1-p) \geq 10\)).
The two groups that are being compared must be unpaired and unrelated (i.e., independent).
Below are the possible null and alternative hypothesis pairs:
| Research Question | Are the proportions of group 1 and group 2 different? | Is the proportion of group 1 greater than the proportion of group 2? | Is the proportion of group 1 less than the proportion of group 2? |
|---|---|---|---|
| Null Hypothesis, \(H_{0}\) | \(p_1 - p_2=0\) | \(p_1 - p_2=0\) | \(p_1 - p_2=0\) |
| Alternative Hypothesis, \(H_{a}\) | \(p_1 - p_2 \neq 0\) | \(p_1 - p_2> 0\) | \(p_1 - p_2<0\) |
| Type of Hypothesis Test | Two-tailed, non-directional | Right-tailed, directional | Left-tailed, directional |
The null hypothesis is that there is not a difference between the two proportions (i.e., \(p_1 = p_2\)). If the null hypothesis is true then the population proportions are equal. When computing the standard error for the difference between the two proportions a pooled proportion is used as opposed to the two proportions separately (i.e., unpooled). This pooled estimate will be symbolized by \(\widehat{p}\). This is similar to a weighted mean, but with two proportions.
- Pooled Estimate of \(p\)
- \(\widehat{p}=\dfrac{\widehat{p}_1n_1+\widehat{p}_2n_2}{n_1+n_2}\)
The standard error for the difference between two proportions is symbolized by \(SE_{0}\). The subscript 0 tells us that this standard error is computed under the null hypothesis (\(H_0: p_1-p_2=0\)).
- Standard Error
-
\(SE_0={\sqrt{\dfrac{\widehat{p} (1-\widehat{p})}{n_1}+\dfrac{\widehat{p}(1-\widehat{p})}{n_2}}}=\sqrt{\widehat{p}(1-\widehat{p})\left ( \dfrac{1}{n_1}+\dfrac{1}{n_2} \right )}\)
Note that the default in many statistical programs, including Minitab, is to estimate the two proportions separately (i.e., unpooled). In order to obtain results using the pooled estimate of the proportion you will need to change the method.
Also note that this standard error is different from the one that you used when constructing a confidence interval for \(p_1-p_2\). While the hypothesis testing procedure is based on the null hypothesis that \(p_1-p_2=0\), the confidence interval approach is not based on this premise. The hypothesis testing approach uses the pooled estimate of \(p\) while the confidence interval approach will use an unpooled method.
- Test Statistic for Two Independent Proportions
- \(z=\dfrac{\widehat{p}_1-\widehat{p}_2}{SE_0}\)
The \(z\) test statistic found in Step 2 is used to determine the \(p\) value. The \(p\) value is the proportion of the \(z\) distribution (normal distribution with a mean of 0 and standard deviation of 1) that is more extreme than the test statistic in the direction of the alternative hypothesis.
If \(p \leq \alpha\) reject the null hypothesis. If \(p>\alpha\) fail to reject the null hypothesis.
Based on your decision in Step 4, write a conclusion in terms of the original research question.
9.1.2.1.1 – Example: Ice Cream
9.1.2.1.1 – Example: Ice CreamExample: Ice Cream
The Creamery wants to compare adults and children in terms of preference for eating their ice cream out of a cone. They take a representative sample of 500 customers (240 adults and 260 children) and ask if they prefer cones over bowls. They found that 124 adults preferred cones and 90 children preferred cones.
\(H_0: p_a - p_c = 0\)
\(H_a:p_a - p_c \ne 0\)
Check assumptions:
\(n_a \hat{p}_a = 124\)
\(n_a (1-\widehat p_a) = 240 - 124 = 116\)
\(n_c \widehat p_c = 90\)
\(n_c (1-\widehat p_c) = 260-90 = 170\)
These counts are all at least 10 so we can use the normal approximation method.
Pooled Estimate of \(p\)
\(\widehat{p}=\dfrac{\widehat{p}_1n_1+\widehat{p}_2n_2}{n_1+n_2}\)
\(\widehat{p}=\dfrac{124+90}{240+260}=\dfrac{214}{500}=0.428\)
Standard Error of \(\hat{p}\)
\(SE_{0}={\sqrt{\frac{\widehat{p} (1-\widehat{p})}{n_1}+\frac{\widehat{p}(1-\widehat{p})}{n_2}}}=\sqrt{\widehat{p}(1-\widehat{p})\left ( \frac{1}{n_1}+\frac{1}{n_2} \right )}\)
\(SE_{0}=\sqrt{0.428(1-0.428)\left ( \dfrac{1}{240}+\dfrac{1}{260} \right )}=0.04429\)
Test Statistic for Two Independent Proportions
\(z=\dfrac{\widehat{p}_1-\widehat{p}_2}{SE_0}\)
\(z=\dfrac{\dfrac{124}{240}-\dfrac{90}{260}}{0.04429}=3.850\)
This is a two-tailed test. Our p-value will be the area of the \(z\) distribution more extreme than \(3.850\).
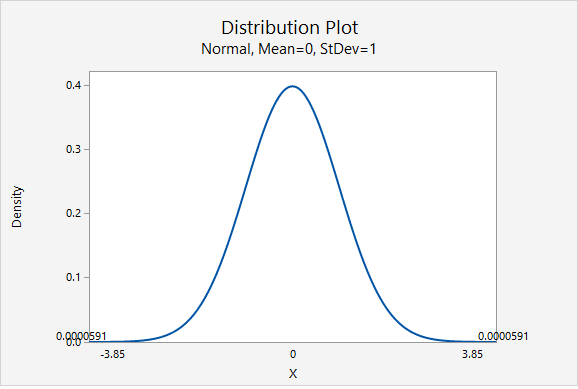
\(p = 0.0000591 \times 2 = 0.0001182\)
\(p \le 0.05\)
Reject the null hypothesis
There is convincing evidence that, in the population of Creamery customers, the proportion of adults who prefer cones is different from the proportion of children who prefer cones in the population.
9.1.2.1.2 – Example: Same Sex Marriage
9.1.2.1.2 – Example: Same Sex MarriageExample: Same Sex Marriage
A survey was given to a random sample of college students. They were asked whether they think same sex marriage should be legal. We're going to compare the students who identified as women and men in terms of whether or not they responded "yes" to this question. Of the 251 women in the sample, 185 said "yes." Of the 199 men in the sample, 107 said "yes."
For women, there were 185 who said "yes" and 66 who said "no." For men, there were 107 who said "yes" and 92 who said "no." There are at least 10 successes and failures in each group so the normal approximation method can be used.
\(\widehat{p}_{w}=\dfrac{185}{251}\)
\(\widehat{p}_{m}=\dfrac{107}{199}\)
This is a two-tailed test because we are looking for a difference between women and men, we were not given a specific direction.
- \( H_{0} : p_{w}- p_{m}=0 \)
- \( H_{a} : p_{w}- p_{m}\neq 0 \)
\(\widehat{p}=\dfrac{185+107}{251+199}=\dfrac{292}{450}=0.6489\)
\(SE_0=\sqrt{\frac{292}{450}\left ( 1-\frac{292}{450} \right )\left ( \frac{1}{251}+\frac{1}{199} \right )}=0.0453\)
\(z=\dfrac{\frac{185}{251}-\frac{107}{199}}{0.0453}=4.400\)
Our test statistic is \(z=4.400\)
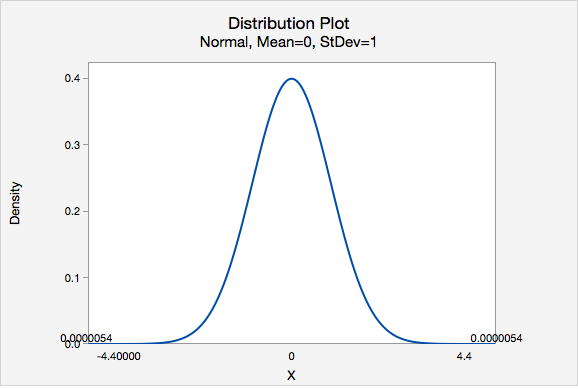
\(P(z>4.400)=0.0000054\), this is a two-tailed test, so this value must be multiplied by two: \(0.0000054\times 2= 0.0000108\)
\(p<0.0001\)
\(p\leq0.05\), therefore we reject the null hypothesis.
There is convincing evidence, in this population of students, that there is a difference between the proportion of women and men who think that same sex marriage should be legal.