11.2.1.2- Cards (Equal Proportions)
11.2.1.2- Cards (Equal Proportions)Example: Cards
Research question: When randomly selecting a card from a deck with replacement, are we equally likely to select a heart, diamond, spade, and club?
I randomly selected a card from a standard deck 40 times with replacement. I pulled 13 hearts, 8 diamonds, 8 spades, and 11 clubs.
Let's use the five-step hypothesis testing procedure:
\(H_0: p_h=p_d=p_s=p_c=0.25\)
\(H_a:\) at least one \(p_i\) is not as specified in the null
We can use the null hypothesis to check the assumption that all expected counts are at least 5.
\(Expected\;count=n (p_i)\)
All \(p_i\) are 0.25. \(40(0.25)=10\), thus this assumption is met and we can approximate the sampling distribution using the chi-square distribution.
\(\chi^2=\sum \dfrac{(Observed-Expected)^2}{Expected} \)
All expected values are 10. Our observed values were 13, 8, 8, and 11.
\(\chi^2=\dfrac{(13-10)^2}{10}+\dfrac{(8-10)^2}{10}+\dfrac{(8-10)^2}{10}+\dfrac{(11-10)^2}{10}\)
\(\chi^2=\dfrac{9}{10}+\dfrac{4}{10}+\dfrac{4}{10}+\dfrac{1}{10}\)
\(\chi^2=1.8\)
Our sampling distribution will be a chi-square distribution.
\(df=k-1=4-1=3\)
We can find the p-value by constructing a chi-square distribution with 3 degrees of freedom to find the area to the right of \(\chi^2=1.8\)
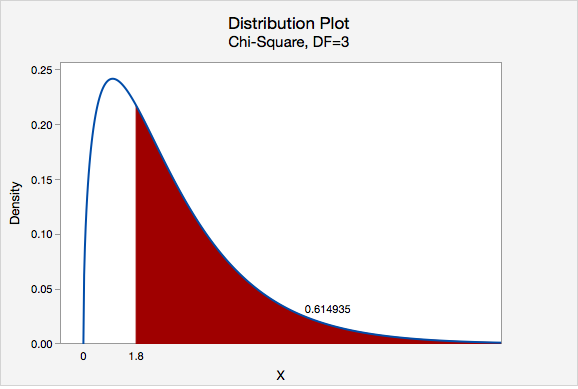
The p-value is 0.614935
\(p>0.05\) therefore we fail to reject the null hypothesis.
There is not enough evidence to state that the proportion of hearts, diamonds, spades, and clubs that are randomly drawn from this deck are different.