12.3 - Simple Linear Regression
12.3 - Simple Linear RegressionRecall from Lesson 3, regression uses one or more explanatory variables (\(x\)) to predict one response variable (\(y\)). In this lesson we will be learning specifically about simple linear regression. The "simple" part is that we will be using only one explanatory variable. If there are two or more explanatory variables, then multiple linear regression is necessary. The "linear" part is that we will be using a straight line to predict the response variable using the explanatory variable.
You may recall from an algebra class that the formula for a straight line is \(y=mx+b\), where \(m\) is the slope and \(b\) is the \(y\)-intercept. The slope is a measure of how steep the line is; in algebra this is sometimes described as "change in \(y\) over change in \(x\)," or "rise over run". A positive slope indicates a line moving from the bottom left to top right. A negative slope indicates a line moving from the top left to bottom right. For every one unit increase in \(x\) the predicted value of \(y\) increases by the value of the slope. The \(y\) intercept is the location on the \(y\) axis where the line passes through; this is the value of \(y\) when \(x\) equals 0.
In statistics, we use a similar formula:
- Simple Linear Regression Line in a Sample
- \(\widehat{y}=b_0 +b_1 x\)
-
\(\widehat{y}\) = predicted value of \(y\) for a given value of \(x\)
\(b_0\) = \(y\)-intercept
\(b_1\) = slope
In the population, the \(y\)-intercept is denoted as \(\beta_0\) and the slope is denoted as \(\beta_1\).
Some textbook and statisticians use slightly different notation. For example, you may see either of the following notations used:
\(\widehat{y}=\widehat{\beta}_0+\widehat{\beta}_1 x \;\;\; \text{or} \;\;\; \widehat{y}=a+b x\)
Note that in all of the equations above, the \(y\)-intercept is the value that stands alone and the slope is the value attached to \(x\).
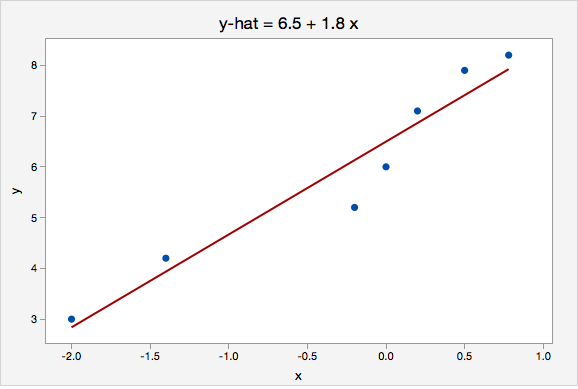
Example: Interpreting the Equation for a Line
The plot below shows the line \(\widehat{y}=6.5+1.8x\)
Here, the \(y\)-intercept is 6.5. This means that when \(x=0\) then the predicted value of \(y\) is 6.5.
The slope is 1.8. For every one unit increase in \(x\), the predicted value of \(y\) increases by 1.8.
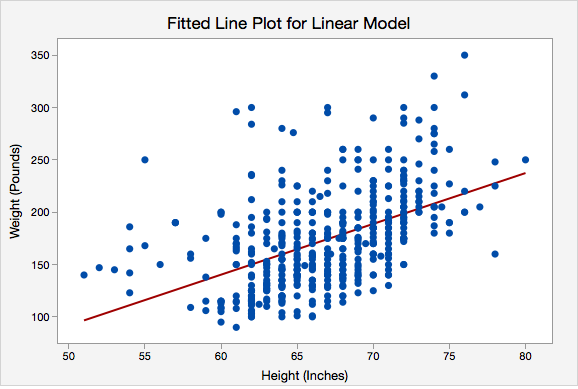
Example: Interpreting the Regression Line Predicting Weight with Height
Data were collected from a random sample of World Campus STAT 200 students. The plot below shows the regression line \(\widehat{weight}=-150.950+4.854(height)\)
Here, the \(y\)-intercept is -150.950. This means that an individual who is 0 inches tall would be predicted to weigh -150.905 pounds. In this particular scenario this intercept does not have any real applicable meaning because our range of heights is about 50 to 80 inches. We would never use this model to predict the weight of someone who is 0 inches tall. What we are really interested in here is the slope.
The slope is 4.854. For every one inch increase in height, the predicted weight increases by 4.854 pounds.
Review: Key Terms
In the next sections you will learn how to construct and test for the statistical significance of a simple linear regression model. But first, let's review some key terms:
- Explanatory variable
-
Variable that is used to explain variability in the response variable, also known as an independent variable or predictor variable; in an experimental study, this is the variable that is manipulated by the researcher.
- Response variable
-
The outcome variable, also known as a dependent variable.
- Simple linear regression
-
A method for predicting one response variable using one explanatory variable and a constant (i.e., the yy-intercept).
- y-intercept
-
The point on the \(y\)-axis where a line crosses (i.e., value of \(y\) when \(x = 0\)); in regression, also known as the constant.
- Slope
-
A measure of the direction (positive or negative) and steepness of a line; for every one unit increase in \(x\), the change in \(y\). For every one unit increase in \(x\) the predicted value of \(y\) increases by the value of the slope.
12.3.1 - Formulas
12.3.1 - FormulasSimple linear regression uses data from a sample to construct the line of best fit. But what makes a line “best fit”? The most common method of constructing a regression line, and the method that we will be using in this course, is the least squares method. The least squares method computes the values of the intercept and slope that make the sum of the squared residuals as small as possible.
Recall from Lesson 3, a residual is the difference between the actual value of y and the predicted value of y (i.e., \(y - \widehat y\)). The predicted value of y ("\(\widehat y\)") is sometimes referred to as the "fitted value" and is computed as \(\widehat{y}_i=b_0+b_1 x_i\).
Below, we'll look at some of the formulas associated with this simple linear regression method. In this course, you will be responsible for computing predicted values and residuals by hand. You will not be responsible for computing the intercept or slope by hand.
Residuals
Residuals are symbolized by \(\varepsilon \) (“epsilon”) in a population and \(e\) or \(\widehat{\varepsilon }\) in a sample.
As with most predictions, you expect there to be some error. For example, if we are using height to predict weight, we wouldn't expect to be able to perfectly predict every individuals weight using their height. There are many variables that impact a person's weight, and height is just one of those many variables. These errors in regression predictions are called prediction error or residuals.
A residual is calculated by taking an individual's observed y value minus their corresponding predicted y value. Therefore, each individual has a residual. The goal in least squares regression is to construct the regression line that minimizes the squared residuals. In essence, we create a best fit line that has the least amount of error.
- Residual
- \(e_i =y_i -\widehat{y}_i\)
-
\(y_i\) = actual value of y for the ith observation
\(\widehat{y}_i\) = predicted value of y for the ith observation
- Sum of Squared Residuals
-
Also known as Sum of Squared Errors (SSE)
\(SSE=\sum (y-\widehat{y})^2\)
Computing the Intercept & Slope
Statistical software will compute the values of the \(y\)-intercept and slope that minimize the sum of squared residuals. The conceptual formulas below show how these statistics are related to one another and how they relate to correlation which you learned about earlier in this lesson. In this course we will always be using Minitab to compute these values.
- Slope
- \(b_1 =r \dfrac{s_y}{s_x}\)
-
\(r\) = Pearson’s correlation coefficient between \(x\) and \(y\)
\(s_y\) = standard deviation of \(y\)
\(s_x\) = standard deviation of \(x\)
- y-intercept
- \(b_0=\overline {y} - b_1 \overline {x}\)
-
\(\overline {y}\) = mean of \(y\)
\(\overline {x}\) = mean of \(x\)
\(b_1\) = slope
Review of New Terms
Before we continue, let’s review a few key terms:
- Least squares method
- Method of constructing a regression line which makes the sum of squared residuals as small as possible for the given data.
- Predicted Value
- Symbolized as \(\widehat y\) ("y-hat") and also known as the "fitted value," the expected value of y for a given value of x
- Residual
- Symbolized as \(\varepsilon \) (“epsilon”) in a population and \(e\) or \(\widehat{\varepsilon }\) in a sample, an individual's observed y value minus their predicted y value (i.e., \(e=y- \widehat{y}\)); on a scatterplot, this is the vertical distance between the observed y value and the regression line
- Sum of squared residuals
- Also known as the sum of squared errors ("SSE"), the sum of all of the residuals squared: \(\sum (y-\widehat{y})^2\).
12.3.2 - Assumptions
12.3.2 - AssumptionsIn order to use the methods above, there are four assumptions that must be met:
- Linearity: The relationship between \(x\) and y must be linear. Check this assumption by examining a scatterplot of \(x\) and \(y\).
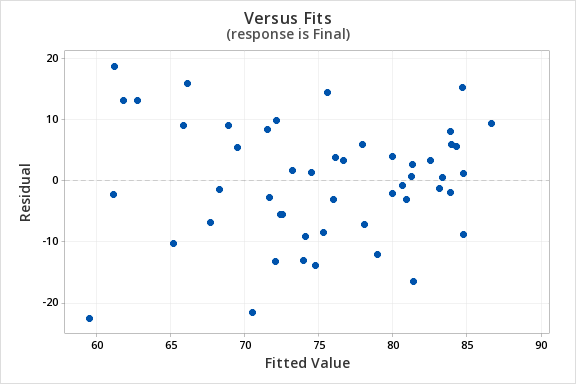
- Independence of errors: There is not a relationship between the residuals and the predicted values. Check this assumption by examining a scatterplot of “residuals versus fits.” The correlation should be approximately 0.
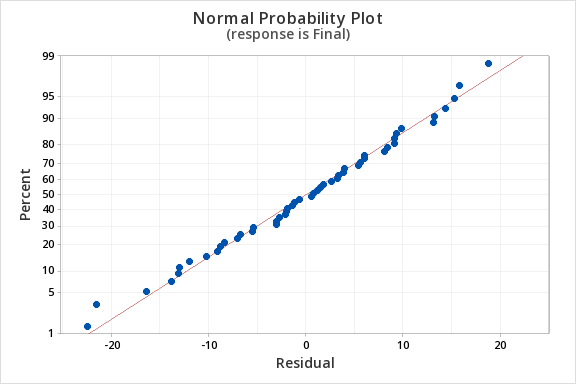
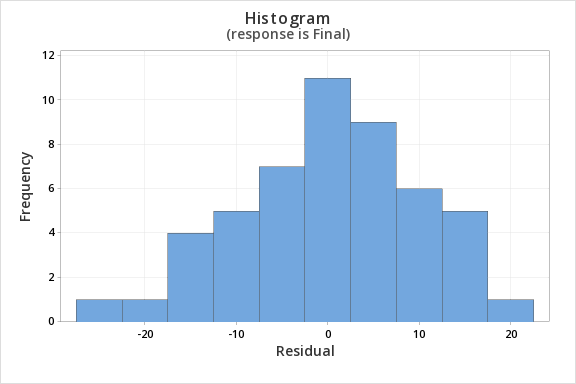
- Normality of errors: The residuals must be approximately normally distributed. Check this assumption by examining a normal probability plot; the observations should be near the line. You can also examine a histogram of the residuals; it should be approximately normally distributed. The distribution will not be perfectly normal because we're working with sample data and there may be some sampling error, but the distribution should not be clearly skewed.
- Equal variances: The variance of the residuals should be consistent across all predicted values. Check this assumption by examining the scatterplot of “residuals versus fits.” The variance of the residuals should be consistent across the x-axis. If the plot shows a pattern (e.g., bowtie or megaphone shape), then variances are not consistent and this assumption has not been met.
Example: Checking Assumptions
The following example uses students' scores on two tests.
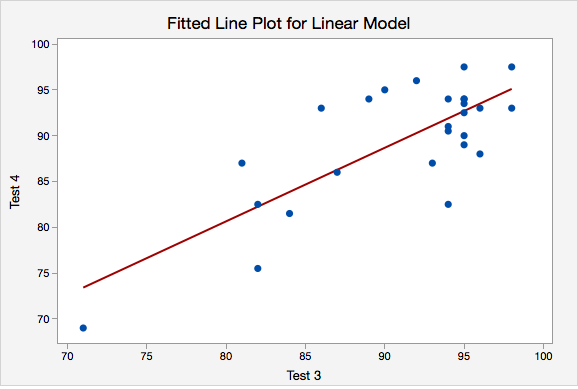
- Linearity. The scatterplot below shows that the relationship between Test 3 and Test 4 scores is linear.
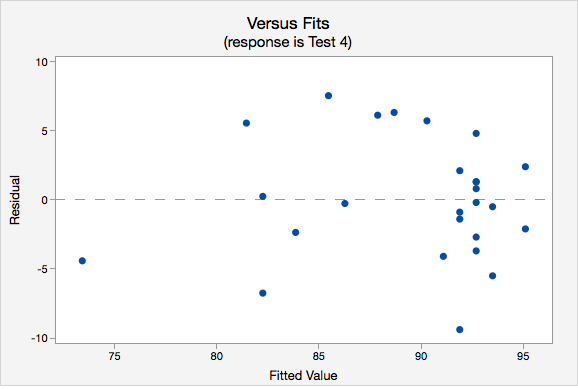
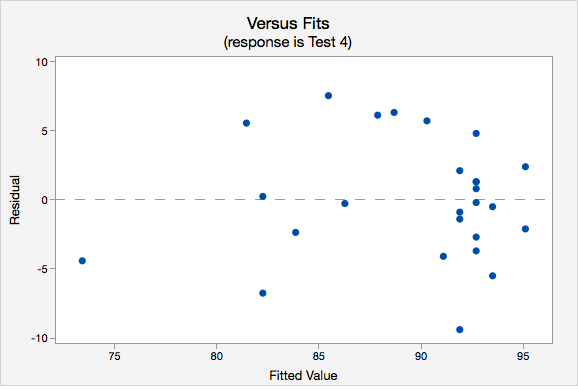
- Independence of errors. The plot of residuals versus fits is shown below. The correlation shown in this scatterplot is approximately \(r=0\), thus this assumption has been met.
- Normality of errors. On the normal probability plot we are looking to see if our observations follow the given line. This tells us that the distribution of residuals is approximately normal. We could also look at the second graph which is a histogram of the residuals; here we see that the distribution of residuals is approximately normal.
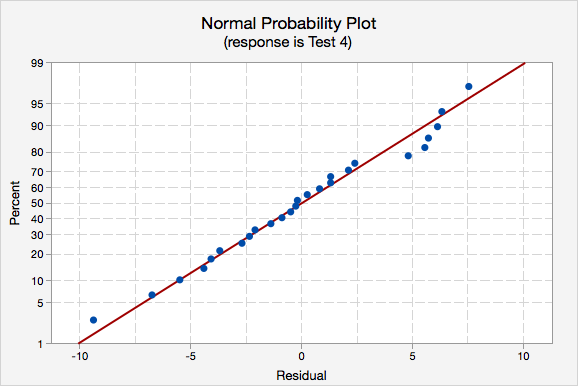
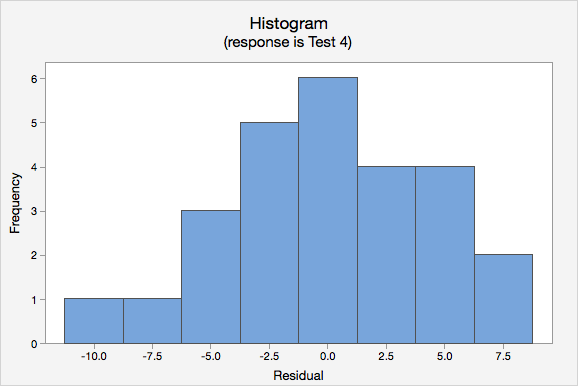
- Equal variance. Again we will use the plot of residuals versus fits. Now we are checking that the variance of the residuals is consistent across all fitted values.
12.3.3 - Minitab - Simple Linear Regression
12.3.3 - Minitab - Simple Linear RegressionMinitab® – Obtaining Simple Linear Regression Output
We previously created a scatterplot of quiz averages and final exam scores and observed a linear relationship. Here, we will use quiz scores to predict final exam scores.
- Open the Minitab file: Exam.mpx
- Select Stat > Regression > Regression > Fit Regression Model...
- Select Final in the box on the left to insert it into the Response box on the right
- Select Quiz_Average in the box on the left to insert it into the Continuous Predictors box on the right
- Under the Graphs tab, click the box for Four in one
- Click OK
This should result in the following output:
Regression Equation
Final = 12.1 + 0.751 Quiz_Average
Coefficients
| Term | Coef | SE Coef | T-Value | P-Value | VIF |
|---|---|---|---|---|---|
| Constant | 12.1 | 11.9 | 1.01 | 0.315 | |
| Quiz_Average | 0.751 | 0.141 | 5.31 | 0.000 | 1.00 |
Model Summary
| S | R-sq | R-sq(adj) | R-sq(pred) |
|---|---|---|---|
| 9.71152 | 37.04% | 35.73% | 29.82% |
Analysis of Variance
| Source | DF | Adj SS | Adj MS | F-Value | P-Value |
|---|---|---|---|---|---|
| Regression | 1 | 2664 | 2663.66 | 28.24 | 0.000 |
| Quiz_Average | 1 | 2664 | 2663.66 | 28.24 | 0.000 |
| Error | 48 | 4527 | 94.31 | ||
| Total | 49 | 7191 |
Fits and Diagnostics for Unusual Observations
| Obs | Final | Fit | Resid | Std Resid | |
|---|---|---|---|---|---|
| 11 | 49.00 | 70.50 | -21.50 | -2.25 | R |
| 40 | 80.00 | 61.22 | 18.78 | 2.03 | R |
| 47 | 37.00 | 59.51 | -22.51 | -2.46 | R |
R Large residual
On the next page you will learn how to test for the statistical significance of the slope.
12.3.4 - Hypothesis Testing for Slope
12.3.4 - Hypothesis Testing for SlopeWe can use statistical inference (i.e., hypothesis testing) to draw conclusions about how the population of \(y\) values relates to the population of \(x\) values, based on the sample of \(x\) and \(y\) values.
The equation \(Y=\beta_0+\beta_1 x\) describes this relationship in the population. Within this model there are two parameters that we use sample data to estimate: the \(y\)-intercept (\(\beta_0\) estimated by \(b_0\)) and the slope (\(\beta_1\) estimated by \(b_1\)). We can use the five step hypothesis testing procedure to test for the statistical significance of each separately. Note, typically we are only interested in testing for the statistical significance of the slope because that tells us that \(\beta_1 \neq 0\) which means that \(x\) can be used to predict \(y\). When \(\beta_1 = 0\) then the line of best fit is a straight horizontal line and having information about \(x\) does not change the predicted value of \(y\); in other words, \(x\) does not help us to predict \(y\). If the value of the slope is anything other than 0, then the predict value of \(y\) will be different for all values of \(x\) and having \(x\) helps us to better predict \(y\).
We are usually not concerned with the statistical significance of the \(y\)-intercept unless there is some theoretical meaning to \(\beta_0 \neq 0\). Below you will see how to test the statistical significance of the slope and how to construct a confidence interval for the slope; the procedures for the \(y\)-intercept would be the same.
The assumptions of simple linear regression are linearity, independence of errors, normality of errors, and equal error variance. You should check all of these assumptions before preceding.
| Research Question | Is the slope in the population different from 0? | Is the slope in the population positive? | Is the slope in the population negative? |
|---|---|---|---|
| Null Hypothesis, \(H_{0}\) | \(\beta_1 =0\) | \(\beta_1= 0\) | \(\beta_1= 0\) |
| Alternative Hypothesis, \(H_{a}\) | \(\beta_1\neq 0\) | \(\beta_1> 0\) | \(\beta_1< 0\) |
| Type of Hypothesis Test | Two-tailed, non-directional | Right-tailed, directional | Left-tailed, directional |
Minitab will compute the \(t\) test statistic:
\(t=\dfrac{b_1}{SE(b_1)}\) where \(SE(b_1)=\sqrt{\dfrac{\dfrac{\sum (e^2)}{n-2}}{\sum (x- \overline{x})^2}}\)
Minitab will compute the p-value for the non-directional hypothesis \(H_a: \beta_1 \neq 0 \)
If you are conducting a one-tailed test you will need to divide the p-value in the Minitab output by 2.
If \(p\leq \alpha\) reject the null hypothesis. If \(p>\alpha\) fail to reject the null hypothesis.
Based on your decision in Step 4, write a conclusion in terms of the original research question.
12.3.4.1 - Example: Quiz and exam scores
12.3.4.1 - Example: Quiz and exam scoresConstruct a model using quiz averages to predict final exam scores.
This example uses the exam data set found in this Minitab file: Exam.mpx
- \(H_0\colon \beta_1 =0\)
- \(H_a\colon \beta_1 \neq 0\)
The scatterplot below shows that the relationship between quiz average and final exam score is linear (or at least it's not non-linear).
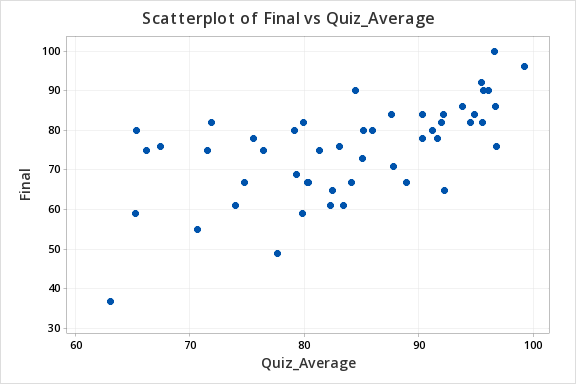
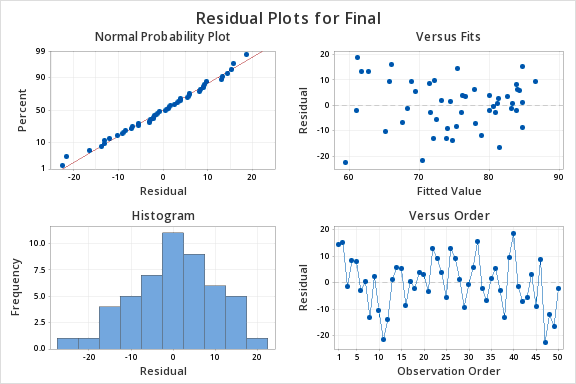
The plot of residuals versus fits below can be used to check the assumptions of independent errors and equal error variances. There is not a significant correlation between the residuals and fits, therefore the assumption of independent errors has been met. The variance of the residuals is relatively consistent for all fitted values, therefore the assumption of equal error variances has been met.
Finally, we must check for the normality of errors. We can use the normal probability plot below to check that our data points fall near the line. Or, we can use the histogram of residuals below to check that the errors are approximately normally distributed.
Now that we have check all of the assumptions of simple linear regression, we can examine the regression model.
We will use the coefficients table from the Minitab output.
Coefficients
Term | Coef | SE Coef | T-Value | P-Value | VIF |
|---|---|---|---|---|---|
Constant | 12.1 | 11.9 | 1.01 | 0.315 | |
Quiz_Average | 0.751 | 0.141 | 5.31 | 0.000 | 1.00 |
\(t = 5.31\)
\(p=0.000\)
\(p < \alpha\), reject the null hypothesis
There is convincing evidence that that students' quiz averages can be used to predict their final exam scores in the population.
12.3.4.2 - Example: Business Decisions
12.3.4.2 - Example: Business DecisionsA student-run cafe wants to use data to determine how many wraps they should make today. If they make too many wraps they will have waste. But, if they don't make enough wraps they will lose out on potential profit. They have been collecting data concerning their daily sales as well as data concerning the daily temperature. They found that there is a statistically significant relationship between daily temperature and coffee sales. So, the students want to know if a similar relationship exists between daily temperature and wrap sales. The video below will walk you through the process of using simple linear regression to determine if the daily temperature can be used to predict wrap sales. The screenshots and annotation below the video will walk you through these steps again.
Can daily temperature be used to predict wrap sales?
Data concerning sales at a student-run cafe were obtained from a Journal of Statistics Education article. Data were retrieved from cafedata.xls more information about this data set available at cafedata.txt.
For the analysis you can use the Minitab file: cafedata.mpx
- \(H_0\colon \beta_1 =0\)
- \(H_a\colon \beta_1 \neq 0\)
The scatterplot below shows that the relationship between maximum daily temperature and wrap sales is linear (or at least it's not non-linear). Though the relationship appears to be weak.
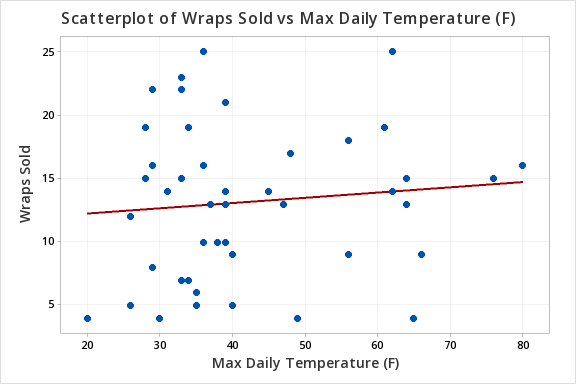
The plot of residuals versus fits below can be used to check the assumptions of independent errors and equal error variances. There is not a significant correlation between the residuals and fits, therefore the assumption of independent errors has been met. The variance of the residuals is relatively consistent for all fitted values, therefore the assumption of equal error variances has been met.
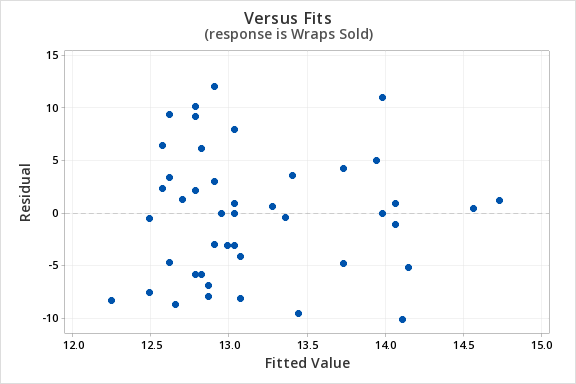
Finally, we must check for the normality of errors. We can use the normal probability plot below to check that our data points fall near the line. Or, we can use the histogram of residuals below to check that the errors are approximately normally distributed.
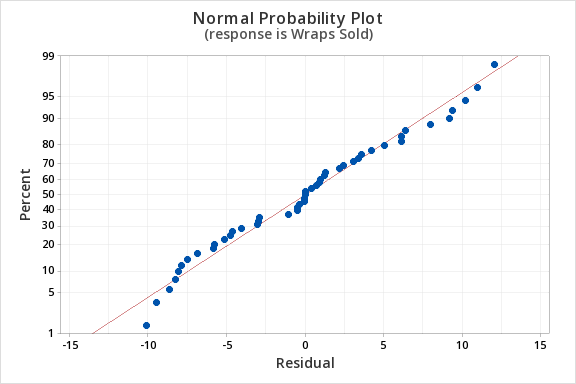
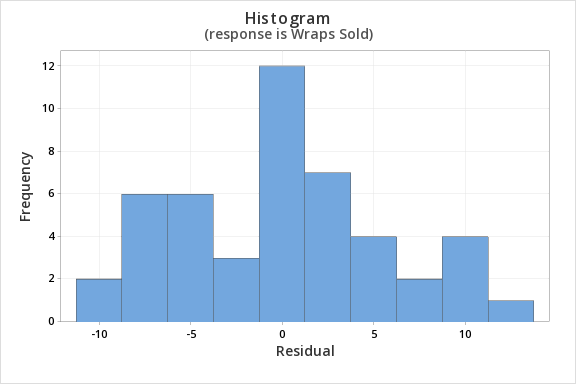
Now that we have check all of the assumptions of simple linear regression, we can examine the regression model.
Regression Equation
Wraps Sold = 11.42 + 0.0414 Max Daily Temperature (F)
Coefficients
| Term | Coef | SE Coef | T-Value | P-Value | VIF |
|---|---|---|---|---|---|
| Constant | 11.42 | 2.66 | 4.29 | 0.000 | |
| Max Daily Temperature (F) | 0.0414 | 0.0603 | 0.69 | 0.496 | 1.00 |
Model Summary
| S | R-sq | R-sq(adj) | R-sq(pred) |
|---|---|---|---|
| 5.90208 | 1.04% | 0.00% | 0.00% |
Analysis of Variance
| Source | DF | Adj SS | Adj MS | F-Value | P-Value |
|---|---|---|---|---|---|
| Regression | 1 | 16.41 | 16.41 | 0.47 | 0.496 |
| Max Daily Temperature (F) | 1 | 16.41 | 16.41 | 0.47 | 0.496 |
| Error | 45 | 1567.55 | 34.83 | ||
| Lack-of-Fit | 24 | 875.17 | 36.47 | 1.11 | 0.411 |
| Pure Error | 21 | 692.38 | 32.97 | ||
| Total | 46 | 1583.96 |
\(t = 0.69\)
\(p=0.496\)
\(p > \alpha\), fail to reject the null hypothesis
There is not enough evidence to conclude that maximum daily temperature can be used to predict the number of wraps sold in the population of all days.
12.3.5 - Confidence Interval for Slope
12.3.5 - Confidence Interval for SlopeWe can use the slope that was computed from our sample to construct a confidence interval for the population slope (\(\beta_1\)). This confidence interval follows the same general form that we have been using:
- General Form of a Confidence Interval
- \(sample statistic\pm(multiplier)\ (standard\ error)\)
- Confidence Interval of \(\beta_1\)
- \(b_1 \pm t^\ast (SE_{b_1})\)
-
\(b_1\) = sample slope
\(t^\ast\) = value from the \(t\) distribution with \(df=n-2\)
\(SE_{b_1}\) = standard error of \(b_1\)
Example: Confidence Interval of \(\beta_1\)
Below is the Minitab output for a regression model using Test 3 scores to predict Test 4 scores. Let's construct a 95% confidence interval for the slope.
| Term | Coef | SE Coef | T-Value | P-Value | VIF |
|---|---|---|---|---|---|
| Constant | 16.37 | 12.40 | 1.32 | 0.1993 | |
| Test 3 | 0.8034 | 0.1360 | 5.91 | <0.0001 | 1.00 |
From the Minitab output, we can see that \(b_1=0.8034\) and \(SE(b_1)=0.1360\)
We must construct a \(t\) distribution to look up the appropriate multiplier. There are \(n-2\) degrees of freedom.
\(df=26-2=24\)
\(t_{24,\;.05/2}=2.064\)
\(b_1 \pm t \times SE(b_1)\)
\(0.8034 \pm 2.064 (0.1360) = 0.8034 \pm 0.2807 = [0.523,\;1.084]\)
We are 95% confident that \(0.523 \leq \beta_1 \leq 1.084 \)
In other words, we are 95% confident that in the population the slope is between 0.523 and 1.084. For every one point increase in Test 3 the predicted value of Test 4 increases between 0.523 and 1.084 points.
12.3.5.1 - Example: Quiz and exam scores
12.3.5.1 - Example: Quiz and exam scoresData from a sample of 50 students were used to build a regression model using quiz averages to predict final exam scores. Construct a 95% confidence interval for the slope.
This example uses the Minitab file: Exam.mpx
We can use the coefficients table that we produced in the previous regression example using the exam data.
Coefficients
| Term | Coef | SE Coef | T-Value | P-Value | VIF |
|---|---|---|---|---|---|
| Constant | 12.1 | 11.9 | 1.01 | 0.315 | |
| Quiz_Average | 0.751 | 0.141 | 5.31 | 0.000 | 1.00 |
The general form of a confidence interval is sample statistic \(\pm\) multiplier(standard error).
We have the following:
- \(b_1\) (sample slope) is 0.751
- t multiplier for degrees of freedom of (50-2) = 48 is 2.01
- The standard error of the slope (\(SE_{b_1}\) is 0.141 from our table
The confidence interval is...
\begin{align} \text{sample statistic} &\pm \text{multiplier*standard error}\\ 0.751 &\pm 2.01 (0.141)\\ 0.751&\pm 0.283 \\ [0.468 &, 1.034] \end{align}
Interpret
I am 95% confident that the slope for this model is between 0.468 and 1.034 in the population.