4.4 - Bootstrap Confidence Interval
4.4 - Bootstrap Confidence IntervalOnce we have a bootstrap sampling distribution there are two methods for constructing a confidence interval:
- The standard deviation of the bootstrap distribution is the standard error which we can use to construct a bootstrap confidence interval. Recall that for a 95% confidence interval, given that the sampling distribution is approximately normal, the 95% confidence interval will be \(sample\ statistic \pm 2 (standard\ error)\).
- For a 95% confidence interval we can find the middle 95% bootstrap statistics. This is known as the percentile method. This is the preferred method because it works regardless of the shape of the sampling distribution.
The standard error method is covered in Section 3.3 of the Lock5 textbook and the percentile method is covered in Section 3.4.
4.4.1 - StatKey: Standard Error Method
4.4.1 - StatKey: Standard Error MethodThe following examples use StatKey to construct bootstrap distributions. When the bootstrap distribution is approximately normally distributed, we can use the standard error method to construct a confidence interval. Recall for a 95% confidence interval: \(statistic \pm 2 (standard\ error)\). The standard error method can only be used when the bootstrap distribution is approximately normal. If the distribution is not approximately normal, then the percentile method must be used.
To construct a bootstrapped confidence interval using the standard error method follow these steps:
- Determine what type of variable(s) you have and what parameters you want to estimate. StatKey will bootstrap a confidence interval for a mean, median, standard deviation, proportion, difference in two means, difference in two proportions, simple linear regression slope, and correlation (Pearson's r).
- Get your sample data into StatKey. There are some built-in datasets and you have the ability to enter in your own data. This procedure varies depending on the test you're conducting. For a proportion you need to enter the number of successes and number of trials. For anything involving quantitative data you will need to copy and paste your data into StatKey (this is the recommended method) or upload it as a txt, csv, or tsv file.
- Generate at least 5,000 bootstrap samples.
- Confirm that your bootstrap distribution is approximately normal. If it's not approximately normal you should consider using the percentile method.
- Use your original sample statistic and the standard error from your bootstrap distribution to construct a confidence interval.
For a 95% confidence interval the formula is \(statistic \pm 2 (standard\ error)\)
It is possible to use the standard error method to construct confidence intervals at levels other than 95% if you have the appropriate multiplier. Later in the course, in Lesson 7, we will learn more about how other multipliers can be found.
4.4.1.1 - Example: Proportion of Lactose Intolerant German Adults
4.4.1.1 - Example: Proportion of Lactose Intolerant German AdultsIn a representative sample of 500 German adults, 78 are lactose intolerant. Use StatKey to construct a 95% confidence interval to estimate the proportion of all German adults who are lactose intolerant.
4.4.1.2 - Example: Difference in Mean Commute Times
4.4.1.2 - Example: Difference in Mean Commute TimesThe following example uses StatKey to compare the average commute times in Atlanta and St. Louis. Commute time is a quantitative variable, and we are examining the difference in two independent (i.e., not match/paired) groups.
4.4.2 - StatKey: Percentile Method
4.4.2 - StatKey: Percentile MethodRegardless of the shape of the bootstrap sampling distribution, we can use the percentile method to construct a confidence interval. Using this method, the 95% confidence interval is the range of points that cover the middle 95% of bootstrap sampling distribution. The following examples use StatKey.
To construct a 95% bootstrap confidence interval using the percentile method follow these steps:
- Determine what type(s) of variable(s) you have and what parameters you want to estimate. StatKey will bootstrap a confidence interval for a mean, median, standard deviation, proportion, different in two means, difference in two proportions, regression slope, and correlation (Pearson's r).
- Get your sample data into StatKey. There are some built-in datasets and you always have the ability to enter in your own data. This procedure varies depending on the test you're conducting. For a proportion, you need to enter the number of successes and number of trials. For anything involving quantitative data you will need to copy and paste your data into StatKey (this is the recommended method) or upload it as a txt, csv, or tsv file.
- Generate at least 5,000 bootstrap samples.
- Check the "Two-Tail" box at the upper left corner of the bootstrap dotplot. By default, this will give you a 95% confidence interval.
The default in StatKey is to construct a 95% confidence interval. You can change the confidence level by clicking the "0.950" in the center and entering the confidence level you want. For example, for a 90% confidence interval you would enter "0.90." Below is a short video demonstrating this.
4.4.2.1 - Example: Correlation Between Quiz & Exam Scores
4.4.2.1 - Example: Correlation Between Quiz & Exam ScoresThe following video constructs a 95% confidence interval for the correlation between STAT 200 students' quiz scores and final exam scores.
These data can be found in
4.4.2.2 - Example: Difference in Dieting by Biological Sex
4.4.2.2 - Example: Difference in Dieting by Biological Sex
4.4.2.3 - Example: One sample mean sodium content
4.4.2.3 - Example: One sample mean sodium contentSodium Content: CI for One Sample Mean
A nutritionist is conducting a study on the sodium content in fast food. They have collected a random sample of 50 different fast-food items from several popular fast-food chains, including burgers, fries, salads, and sandwiches. For each item, the sodium content (in milligrams) is recorded.
The Dietary Guidelines for Americans recommend that adults limit their sodium intake to less than 2300 mg per day. By examining the sodium content in these fast-food items, the nutritionist aims to provide more informed dietary information to their clients so that they can make healthier choices based on the sodium levels found in popular fast foods.
Data: FF_sodium.csv
Construct a 90% confidence interval using the percentile method to estimate the average sodium content (mg) in a single fast-food item.
To construct a 90% bootstrap confidence interval using the percentile method follow these steps:
- Determine what type(s) of variable(s) you have and what parameters you want to estimate.
In this scenario, we are dealing with the average sodium content (mg) which is a single mean. In StatKey, choose Bootstrap Confidence Intervals > CI for Single Mean, Median, St. Dev.
Upload the sample data file into StatKey using the 'Upload File' button.

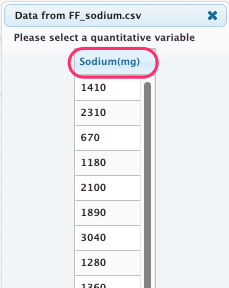
Select the quantitative variable, 'Sodium(mg)' > 'OK'
- Generate at least 5,000 bootstrap samples.
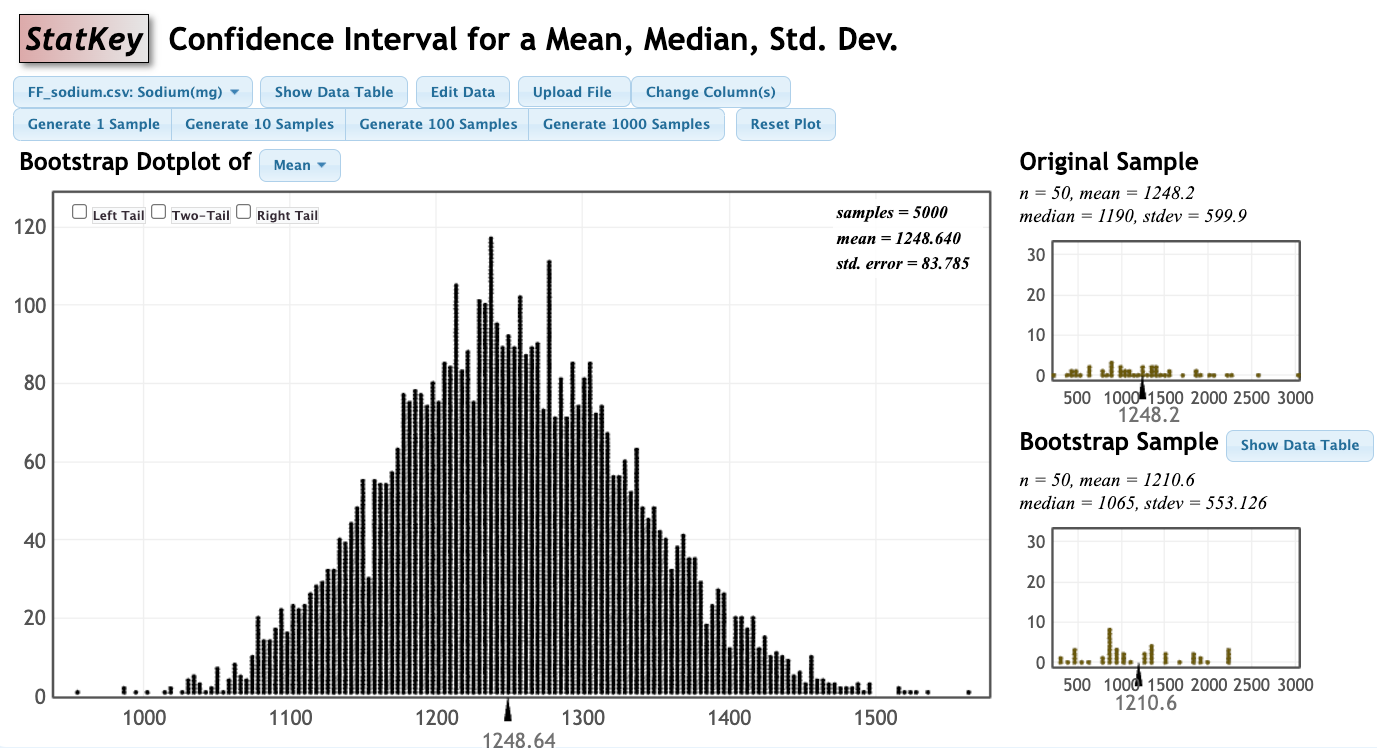
- Check the "Two-Tail" box at the upper left corner of the bootstrap dotplot. By default, this will give you a 95% confidence interval. Select the 0.95 box in the middle and change to 0.90 to display the 90% interval.
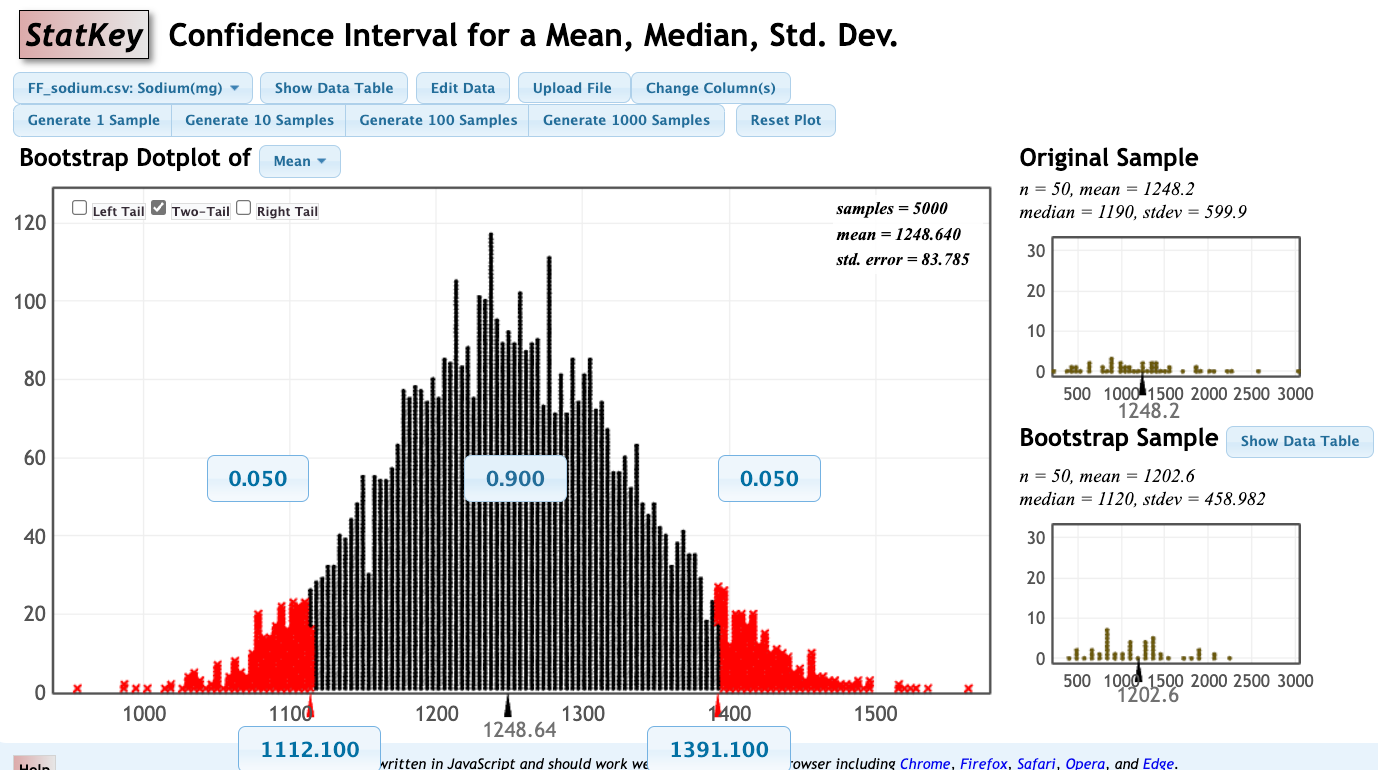
The 90% confidence interval for the average sodium content (mg) of a single fast food item is 1112.1 to 1391.1 mg.