8.2.1 - t Distribution

8.2.1 - t Distribution

The height of the t distribution is determined by the number of degrees of freedom (df). For a one sample mean test, \(df=n-1\).

The first plot below compares the standard normal distribution (i.e., z distribution) to a t distribution. The solid blue line is the standard normal distribution and the dashed red line is a t distribution with 2 degrees of freedom. Here, the tails of the t distribution are higher than the tails of the normal distribution.

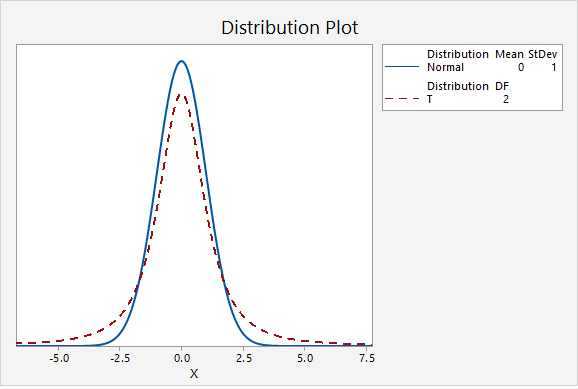
A plot showing the z distribution compared to a t distribution with df=2

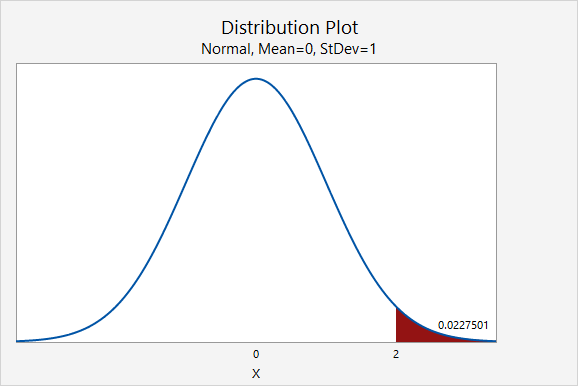
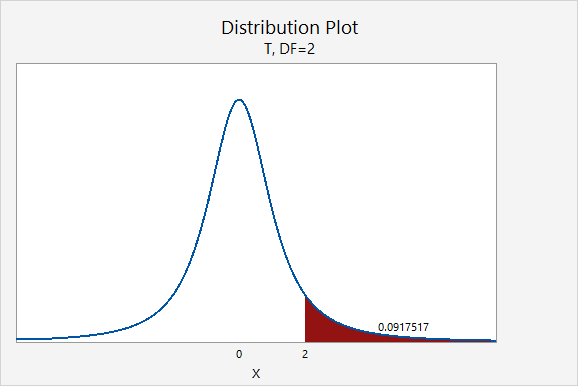
If you think about the area under the curve, the higher tails mean that more area will fall in the tails. For example, as seen in the following two plots, \(P(z>2.00)=0.0227501\) while \(P(t_{df=2}>2.00)=0.0917517\).

Standard normal (i.e., z) distribution showing the area above z=2

Probability distribution plot showing the area greater than t=2 on a distribution with 2 degrees of freedom

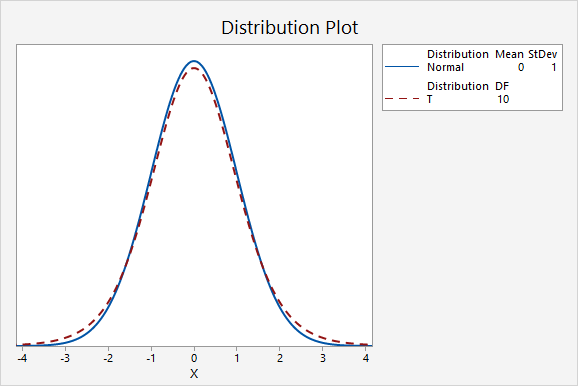
The next plot compares the standard normal distribution to a t distribution with 10 degrees of freedom. Notice that the two distributions are becoming more similar as the sample size increases.

Plot comparing the z distribution to a t distribution with 10 degrees of freedom

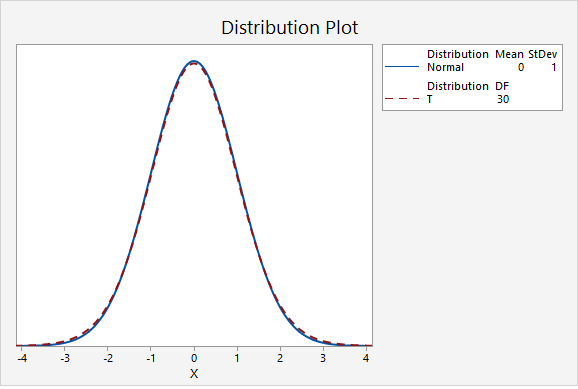
The next plot compares the standard normal distribution to a t distribution with 30 degrees of freedom. 

Plot comparing the standard normal distribution to a t distribution with 30 degrees of freedom

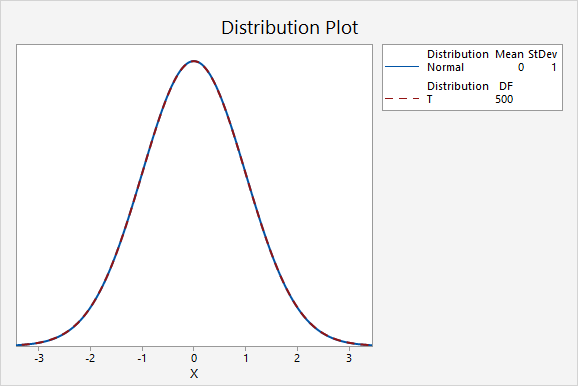
In the final graph, the standard normal distribution is compared to a t distribution with 500 degrees of freedom. Here, the two distributions are nearly identical. As the degrees of freedom approach infinity, the t distribution approaches (i.e., becomes more similar to) the standard normal distribution.

Plot comparing the standard normal distribution to a t distribution with 500 degrees of freedom

Minitab®

The procedures for constructing t distributions in Minitab are similar to those for constructing z distributions. We can construct a probability distribution plot to find the t* multiplier when constructing a confidence interval. And, we can construct a plot to find the p-value when conducting a hypothesis test.

Steps for finding the t* multiplier

  1. In Minitab, select Graph > Probability Distribution Plot > View Probability
  2. Change the Distribution to t
  3. Enter your Degrees of freedom
  4. Select Options
  5. Choose A specified probability
  6. Select Equal tails
  7. For Probability enter the value that is split between the two tails (e.g., for a 90% confidence interval you would enter 0.10)

 

Steps for finding the p value given a t test statistic

  1. In Minitab, select Graph > Probability Distribution Plot > View Probability
  2. Change the Distribution to t
  3. Enter your Degrees of freedom
  4. Select A specified x value
  5. Select Right tail, Left tail, or Equal tails, depending on the direction of your alternative hypothesis 
  6. For X value enter the t test statistic

 

Legend
[1]Link
↥Has Tooltip/Popover
 Toggleable Visibility