4: Confidence Intervals
4: Confidence IntervalsObjectives
- Construct and interpret sampling distributions using StatKey
- Explain the general form of a confidence interval
- Interpret a confidence interval
- Explain the process of bootstrapping
- Construct bootstrap confidence intervals using the standard error method
- Construct bootstrap confidence intervals using the percentile method in StatKey
- Construct bootstrap confidence intervals using Minitab
- Describe how sample size impacts a confidence interval
This lesson corresponds to Chapter 3 in the Lock5 textbook. In Lessons 2 and Lesson 3 you learned about descriptive statistics. Lesson 4 begins our coverage of inferential statistics which use data from a sample to make an inference about a population. Confidence intervals use data collected from a sample to estimate a population parameter.
Confidence Interval
A range computed using sample statistics to estimate an unknown population parameter with a stated level of confidence
In this lesson we will be working with the following statistics and parameters:
Population Parameter | Sample Statistic | |
|---|---|---|
Mean | \(\mu\) | \(\overline x\) |
Difference in two means | \(\mu_1 - \mu_2\) | \(\overline x_1 - \overline x_2\) |
Proportion | \(p\) | \(\widehat p\) |
Difference in two proportions | \(p_1 - p_2\) | \(\widehat p_1 - \widehat p_2\) |
Correlation | \(\rho\) | \(r\) |
Slope (simple linear regression) | \(\beta\) | \(b\) |
Before we begin, let's review population parameters and sample statistics.
Population parameters are fixed values. We rarely know the parameter values because it is often difficult to obtain measures from the entire population.
Sample statistics are known values, but they are random variables because they vary from sample to sample.
Example: Campus Commuters

A survey is carried out at a university to estimate the proportion of undergraduate students who drive to campus to attend classes. One thousand students are randomly selected and asked whether they drive or not to campus to attend classes. The population is all of the undergraduates at that university. The sample is the group of 1000 undergraduate students surveyed. The parameter is the true proportion of all undergraduate students at that university who drive to campus to attend classes. The statistic is the proportion of the 1000 sampled undergraduates who drive to campus to attend classes.
Example: Annual Income in California
A study is conducted to estimate the true mean annual income of all adult residents of California. The study randomly selects 2000 adult residents of California. The population consists of all adult residents of California. The sample is the 2000 residents in the study. The parameter is the true mean annual income of all adult residents of California. The statistic is the mean of the 2000 residents in this sample.
Ultimately, we measure sample statistics and use them to draw conclusions about unknown population parameters. This is statistical inference.
4.1 - Sampling Distributions
4.1 - Sampling DistributionsSample statistics are random variables because they vary from sample to sample. As a result, sample statistics have a distribution called the sampling distribution. The video below demonstrates the construction of a sampling distribution for a known population proportion using StatKey (http://www.lock5stat.com/StatKey/index.html). StatKey is a free online application that we will be using throughout the course.
An important aspect of a sampling distribution is the standard error (SE). The standard error is the standard deviation of a sampling distribution. For a single categorical variable this may be referred to as the standard error of the proportion. For a single quantitative variable this may be referred to as the standard error of the mean. If a sampling distribution is constructed using data from a population, the mean of the sampling distribution will be approximately equal to the population parameter.
- Sampling Distribution
- Distribution of sample statistics with a mean approximately equal to the mean in the original distribution and a standard deviation known as the standard error
- Standard Error
- Standard deviation of a sampling distribution
Note that this method of constructing a sampling distribution requires that we have population data. In most cases we do not know all of the population values. If we did, then we wouldn't need to construct a confidence interval to estimate the population parameter! In those cases we can use bootstrapping methods which you will see in the next section.
As you look through the following examples, note that when the sample size is large the sampling distribution is approximately symmetrical and centered at the population parameter.
4.1.1 - StatKey Examples
4.1.1 - StatKey ExamplesThe process of constructing a sampling distribution from a known population is the same for all types of parameters (i.e., one group proportion, one group mean, difference in two proportions, difference in two means, simple linear regression slope, and correlation). In each case we take a simple random sample of \(n\) from the population without replacement, record the sample statistic of interest, return those observations back into the population, and repeat many times. That distribution of sample statistics is known as the sampling distribution. If the sample size is large, the sampling distribution will be approximately normally with a mean equal to the population parameter.
The following pages include examples of using StatKey to construct sampling distributions for one mean and one proportion.
4.1.1.1 - NFL Salaries (One Mean)
4.1.1.1 - NFL Salaries (One Mean)In this video a sampling distribution is constructed using the "NFL Contracts (2015 in Millions)" dataset that is built into the sampling distribution for a mean feature in StatKey. This dataset includes the salaries of all 2,099 NFL players in 2015 as of the start of that season. We'll construct a sampling distribution given \(n = 5\).
4.1.1.2 - Coin Flipping (One Proportion)
4.1.1.2 - Coin Flipping (One Proportion)We are conducting an experiment in which we are flipping a fair coin 5 times and counting how many times we flip heads. Whether or not the coin lands on heads is a categorical variable with a probability of 0.50. Let's use StatKey to construct a distribution of sample proportions that we could use to determine the probability of any of the possible combinations of successes and failures.
4.1.2 - Copying Data into StatKey
4.1.2 - Copying Data into StatKeyStatKey has a number of built-in datasets. These are great for practicing or for demonstration purposes. In real life, you will have your own datasets that are not built in. For a categorical variable, we can change the population proportion as we did in the example on Lesson 4.1.1.2. For a quantitative variable, we need to copy all of our data into StatKey. The video below walks through an example of copying data from Excel into StatKey. The same procedures can be used to copy data from Minitab, or any other program, into StatKey.
This example uses data from
4.1.3 - Impact of Sample Size
4.1.3 - Impact of Sample SizeThere is an inverse relationship between sample size and standard error. In other words, as the sample size increases, the variability of sampling distribution decreases.
Also, as the sample size increases the shape of the sampling distribution becomes more similar to a normal distribution regardless of the shape of the population.
The built-in dataset "NFL Contracts (2015 in millions)" was used to construct the two sampling distributions below. In the first, a sample size of 10 was used. In the second, a sample size of 100 was used.
Sample size of 10:
Sample size of 100:
With a sample size of 10, the standard error of the mean was 0.936. With a sample size of 100 the standard error of the mean was 0.296. When the sample size increased the standard error decreased.
Also know that the population was strongly skewed to the right. With the smaller sample size, the sampling distribution was also skewed to the right, though not as strongly skewed as the population. With the larger sample size, the sampling distribution was approximately normal.
Example: Proportion of College Graduates
The built-in dataset "College Graduates" was used to construct the two sampling distributions below. In the first, a sample size of 10 was used. In the second, a sample size of 100 was used.
Sample size of 10:
Sample size of 100:
With a sample size of 10, the standard error of the mean was 0.143. With a sample size of 100 the standard error of the mean was 0.044. As the sample size increased the standard error decreased.
Also note how the shape of the sampling distribution changed. With the smaller sample size there were large gaps between each possible sample proportion. When the sample size increased, the gaps between the possible sampling proportions decreased. With the larger sampling size the sampling distribution approximates a normal distribution.
4.2 - Introduction to Confidence Intervals
4.2 - Introduction to Confidence IntervalsIn Lesson 4.1 we learned how to construct sampling distributions when population values were known. In real life, we don't typically have access to the whole population. In these cases we can use the sample data that we do have to construct a confidence interval to estimate the population parameter with a stated level of confidence. This is one type of statistical inference.
- Confidence Interval
- A range computed using sample statistics to estimate an unknown population parameter with a stated level of confidence
Example: Statistical Anxiety
The statistics professors at a university want to estimate the average statistics anxiety score for all of their undergraduate students. It would be too time consuming and costly to give every undergraduate student at the university their statistics anxiety survey. Instead, they take a random sample of 50 undergraduate students at the university and administer their survey.
Using the data collected from the sample, they construct a 95% confidence interval for the mean statistics anxiety score in the population of all university undergraduate students. They are using \(\bar{x}\) to estimate \(\mu\). If the 95% confidence interval for \(\mu\) is 26 to 32, then we could say, “we are 95% confident that the mean statistics anxiety score of all undergraduate students at this university is between 26 and 32.” In other words, we are 95% confident that \(26 \leq \mu \leq 32\). This may also be written as \(\left [ 26,32 \right ]\).
At the center of a confidence interval is the sample statistic, such as a sample mean or sample proportion. This is known as the point estimate. The width of the confidence interval is determined by the margin of error. The margin of error is the amount that is subtracted from and added to the point estimate to construct the confidence interval.
- Point Estimate
- Sample statistic that serves as the best estimate for a population parameter
- Margin of Error
- Half of the width of a confidence interval; equal to the multiplier times the standard error
- General Form of Confidence Interval
- \(sample\ statistic \pm margin\ of\ error\)
- \(margin\ of\ error=multiplier(standard\ error)\)
The margin of error will depend on two factors:
- The level of confidence which determines the multiplier
- The value of the standard error
In Lesson 2 you first learned about the Empirical Rule which states that approximately 95% of observations on a normal distribution fall within two standard deviations of the mean. Thus, when constructing a 95% confidence interval we can use a multiplier of 2.
- General Form of 95% Confidence Interval
- Given a normal distribution, a 95% CI can be found by using...
- \(sample\ statistic\pm2\ (standard\ error)\)
Example: Proportion of Dog Owners

At the beginning of the Spring 2017 semester a representative sample of 501 STAT 200 students were surveyed and asked if they owned a dog. The sample proportion was 0.559. Bootstrapping methods, which we will learn later in this lesson, were used to compute a standard error of 0.022. Assume the bootstrap distribution is normally distributed. We can use this information to construct a 95% confidence interval for the proportion of all STAT 200 students who own a dog.
\(sample\ statistic\pm2\ (standard\ error)\)
0.559 ± 2(0.022)
0.559 ± 0.044
[0.515, 0.603]
I am 95% confident that the proportion of all STAT 200 students in Spring 2017 that own a dog is between 0.515 and 0.603.
Example: Mean Height
In a random sample of 525 Penn State World Campus students the mean height was 67.009 inches with a standard deviation of 4.462 inches. The standard error was computed to be 0.195. Construct a 95% confidence interval for the mean height of all Penn State World Campus students. Assume the bootstrap distribution is normally distributed.
\(sample\ statistic\pm2\ (standard\ error)\)
67.009 ± 2(0.195)
67.009 ± 0.390
[66.619, 67.399]
I am 95% confident that the mean height of all Penn State World Campus students is between 66.619 inches and 67.399 inches.
4.2.1 - Interpreting Confidence Intervals
4.2.1 - Interpreting Confidence IntervalsConfidence intervals are often misinterpreted. The logic behind them may be a bit confusing. Remember that when we're constructing a confidence interval we are estimating a population parameter when we only have data from a sample. We don't know if our sample statistic is less than, greater than, or approximately equal to the population parameter. And, we don't know for sure if our confidence interval contains the population parameter or not.
For example, the correct interpretation of a 95% confidence interval, [L, U], is that "we are 95% confident that the [population parameter] is between [L] and [U]."
Fill in the population parameter with the specific language from the problem. The L represents the 'lower endpoint' of the CI and the U represents the 'upper endpoint.'
Example: Correlation Between Height and Weight
At the beginning of the Spring 2017 semester a sample of World Campus students were surveyed and asked for their height and weight. In the sample, Pearson's r = 0.487. A 95% confidence interval was computed of [0.410, 0.559].
Interpretation:
The correct interpretation of this confidence interval is that we are 95% confident that the correlation between height and weight in the population of all World Campus students is between 0.410 and 0.559.
Example: Seatbelt Usage
A sample of 12th grade females was surveyed about their seatbelt usage. A 95% confidence interval for the proportion of all 12th grade females who always wear their seatbelt was computed to be [0.612, 0.668].
Interpretation:
The correct interpretation of this confidence interval is that we are 95% confident that the proportion of all 12th grade females who always wear their seatbelt in the population is between 0.612 and 0.668.
Example: IQ Scores
A random sample of 50 students at one school was obtained and each selected student was given an IQ test. These data were used to construct a 95% confidence interval of [96.656, 106.422].
Interpretation:
The correct interpretation of this confidence interval is that we are 95% confident that the mean IQ score in the population of all students at this school is between 96.656 and 106.422.
4.2.2 - Applying Confidence Intervals
4.2.2 - Applying Confidence IntervalsA confidence interval contains a range of acceptable estimates of the population parameter. Values in a confidence interval are reasonable estimates for the true population value. Values not in the confidence interval are not reasonable estimates for the population value.
Example: Correlation Between Height and Weight
At the beginning of the Spring 2017 semester a sample of World Campus students were surveyed and asked for their height and weight. In the sample, Pearson's r = 0.487. A 95% confidence interval was computed of [0.410, 0.559].
Research question: Is there convincing evidence of a positive correlation between height and weight in the population of all World Campus students?
The entire confidence interval is greater than zero which means that all reasonable estimates of the population correlation are positive. Yes, there is convincing evidence of a positive correlation between height and weight in the population of all World Campus students.
Example: Seatbelt Usage

A sample of 12th grade females was surveyed about their seatbelt usage. A 95% confidence interval for the proportion of all 12th grade females who always wear their seatbelt was computed to be [0.612, 0.668].
Research question: Is there convincing evidence that the proportion of all 12th grade females who always wear their seatbelt is different from 0.65?
The value of 0.65 is contained within our confidence interval. This means that 0.65 is a reasonable value of the population proportion. We cannot conclude that the population proportion is different from 0.65.
Example: IQ Scores
A random sample of 50 students at one school was obtained and each selected student was given an IQ test. These data were used to construct a 95% confidence interval of [96.656, 106.422].
Research question: Is there convincing evidence that the mean IQ score at this school is different from the known national average of 100?
The 95% confidence interval contains 100. This means that 100 is a reasonable estimate for the mean IQ score of students at this school. There is not enough evidence that the mean at this school is different from 100.
4.3 - Introduction to Bootstrapping
4.3 - Introduction to BootstrappingIn order to construct a confidence interval we need information about the sampling distribution. In Lesson 4.1 we saw how we could construct a sampling distribution when population values were known. What if population values are not known? This is usually the case. If we have sample data, then we can use bootstrapping methods to construct a bootstrap sampling distribution to construct a confidence interval.
Bootstrapping is a resampling procedure that uses data from one sample to generate a sampling distribution by repeatedly taking random samples from the known sample.
- Bootstrapping
- A resampling procedure for constructing a sampling distribution using data from a sample
Example: Bootstrap Distribution for Mean Height
We have data concerning the heights of individuals in a random sample of \(n=15\). To construct a bootstrap distribution for the mean height we would first randomly select one individual from that sample and record their height. Then, with the that individual placed back into the sample, we would randomly select a second individual and record their height. This is known as "sampling with replacement" because we are putting each case back into the sample after recording their height. We would repeat this process until we have selected 15 values. Because we are sampling with replacement, some individuals may appear in the bootstrap sample more than once. We would use those 15 selected values to compute a bootstrapped sample mean. This process is repeated many times. The distribution of many bootstrapped sample means is known as the bootstrap distribution or bootstrap sampling distribution.
The following pages include additional video examples that use StatKey to demonstrate the construction of bootstrap sampling distributions.
4.3.1 - Example: Bootstrap Distribution for Proportion of Peanuts
4.3.1 - Example: Bootstrap Distribution for Proportion of PeanutsThis video uses a dataset built into StatKey to demonstrate the construction of a bootstrap sampling distribution for a single proportion.
4.3.2 - Example: Bootstrap Distribution for Difference in Mean Exercise
4.3.2 - Example: Bootstrap Distribution for Difference in Mean ExerciseThis video uses a dataset built into StatKey to demonstrate the construction of a bootstrap distribution for the difference in two groups' means.
4.4 - Bootstrap Confidence Interval
4.4 - Bootstrap Confidence IntervalOnce we have a bootstrap sampling distribution there are two methods for constructing a confidence interval:
- The standard deviation of the bootstrap distribution is the standard error which we can use to construct a bootstrap confidence interval. Recall that for a 95% confidence interval, given that the sampling distribution is approximately normal, the 95% confidence interval will be \(sample\ statistic \pm 2 (standard\ error)\).
- For a 95% confidence interval we can find the middle 95% bootstrap statistics. This is known as the percentile method. This is the preferred method because it works regardless of the shape of the sampling distribution.
The standard error method is covered in Section 3.3 of the Lock5 textbook and the percentile method is covered in Section 3.4.
4.4.1 - StatKey: Standard Error Method
4.4.1 - StatKey: Standard Error MethodThe following examples use StatKey to construct bootstrap distributions. When the bootstrap distribution is approximately normally distributed, we can use the standard error method to construct a confidence interval. Recall for a 95% confidence interval: \(statistic \pm 2 (standard\ error)\). The standard error method can only be used when the bootstrap distribution is approximately normal. If the distribution is not approximately normal, then the percentile method must be used.
To construct a bootstrapped confidence interval using the standard error method follow these steps:
- Determine what type of variable(s) you have and what parameters you want to estimate. StatKey will bootstrap a confidence interval for a mean, median, standard deviation, proportion, difference in two means, difference in two proportions, simple linear regression slope, and correlation (Pearson's r).
- Get your sample data into StatKey. There are some built-in datasets and you have the ability to enter in your own data. This procedure varies depending on the test you're conducting. For a proportion you need to enter the number of successes and number of trials. For anything involving quantitative data you will need to copy and paste your data into StatKey (this is the recommended method) or upload it as a txt, csv, or tsv file.
- Generate at least 5,000 bootstrap samples.
- Confirm that your bootstrap distribution is approximately normal. If it's not approximately normal you should consider using the percentile method.
- Use your original sample statistic and the standard error from your bootstrap distribution to construct a confidence interval.
For a 95% confidence interval the formula is \(statistic \pm 2 (standard\ error)\)
It is possible to use the standard error method to construct confidence intervals at levels other than 95% if you have the appropriate multiplier. Later in the course, in Lesson 7, we will learn more about how other multipliers can be found.
4.4.1.1 - Example: Proportion of Lactose Intolerant German Adults
4.4.1.1 - Example: Proportion of Lactose Intolerant German AdultsIn a representative sample of 500 German adults, 78 are lactose intolerant. Use StatKey to construct a 95% confidence interval to estimate the proportion of all German adults who are lactose intolerant.
4.4.1.2 - Example: Difference in Mean Commute Times
4.4.1.2 - Example: Difference in Mean Commute TimesThe following example uses StatKey to compare the average commute times in Atlanta and St. Louis. Commute time is a quantitative variable, and we are examining the difference in two independent (i.e., not match/paired) groups.
4.4.2 - StatKey: Percentile Method
4.4.2 - StatKey: Percentile MethodRegardless of the shape of the bootstrap sampling distribution, we can use the percentile method to construct a confidence interval. Using this method, the 95% confidence interval is the range of points that cover the middle 95% of bootstrap sampling distribution. The following examples use StatKey.
To construct a 95% bootstrap confidence interval using the percentile method follow these steps:
- Determine what type(s) of variable(s) you have and what parameters you want to estimate. StatKey will bootstrap a confidence interval for a mean, median, standard deviation, proportion, different in two means, difference in two proportions, regression slope, and correlation (Pearson's r).
- Get your sample data into StatKey. There are some built-in datasets and you always have the ability to enter in your own data. This procedure varies depending on the test you're conducting. For a proportion, you need to enter the number of successes and number of trials. For anything involving quantitative data you will need to copy and paste your data into StatKey (this is the recommended method) or upload it as a txt, csv, or tsv file.
- Generate at least 5,000 bootstrap samples.
- Check the "Two-Tail" box at the upper left corner of the bootstrap dotplot. By default, this will give you a 95% confidence interval.
The default in StatKey is to construct a 95% confidence interval. You can change the confidence level by clicking the "0.950" in the center and entering the confidence level you want. For example, for a 90% confidence interval you would enter "0.90." Below is a short video demonstrating this.
4.4.2.1 - Example: Correlation Between Quiz & Exam Scores
4.4.2.1 - Example: Correlation Between Quiz & Exam ScoresThe following video constructs a 95% confidence interval for the correlation between STAT 200 students' quiz scores and final exam scores.
These data can be found in
4.4.2.2 - Example: Difference in Dieting by Biological Sex
4.4.2.2 - Example: Difference in Dieting by Biological Sex
4.4.2.3 - Example: One sample mean sodium content
4.4.2.3 - Example: One sample mean sodium contentSodium Content: CI for One Sample Mean
A nutritionist is conducting a study on the sodium content in fast food. They have collected a random sample of 50 different fast-food items from several popular fast-food chains, including burgers, fries, salads, and sandwiches. For each item, the sodium content (in milligrams) is recorded.
The Dietary Guidelines for Americans recommend that adults limit their sodium intake to less than 2300 mg per day. By examining the sodium content in these fast-food items, the nutritionist aims to provide more informed dietary information to their clients so that they can make healthier choices based on the sodium levels found in popular fast foods.
Data: FF_sodium.csv
Construct a 90% confidence interval using the percentile method to estimate the average sodium content (mg) in a single fast-food item.
To construct a 90% bootstrap confidence interval using the percentile method follow these steps:
- Determine what type(s) of variable(s) you have and what parameters you want to estimate.
In this scenario, we are dealing with the average sodium content (mg) which is a single mean. In StatKey, choose Bootstrap Confidence Intervals > CI for Single Mean, Median, St. Dev.
Upload the sample data file into StatKey using the 'Upload File' button.

Select the quantitative variable, 'Sodium(mg)' > 'OK'
- Generate at least 5,000 bootstrap samples.
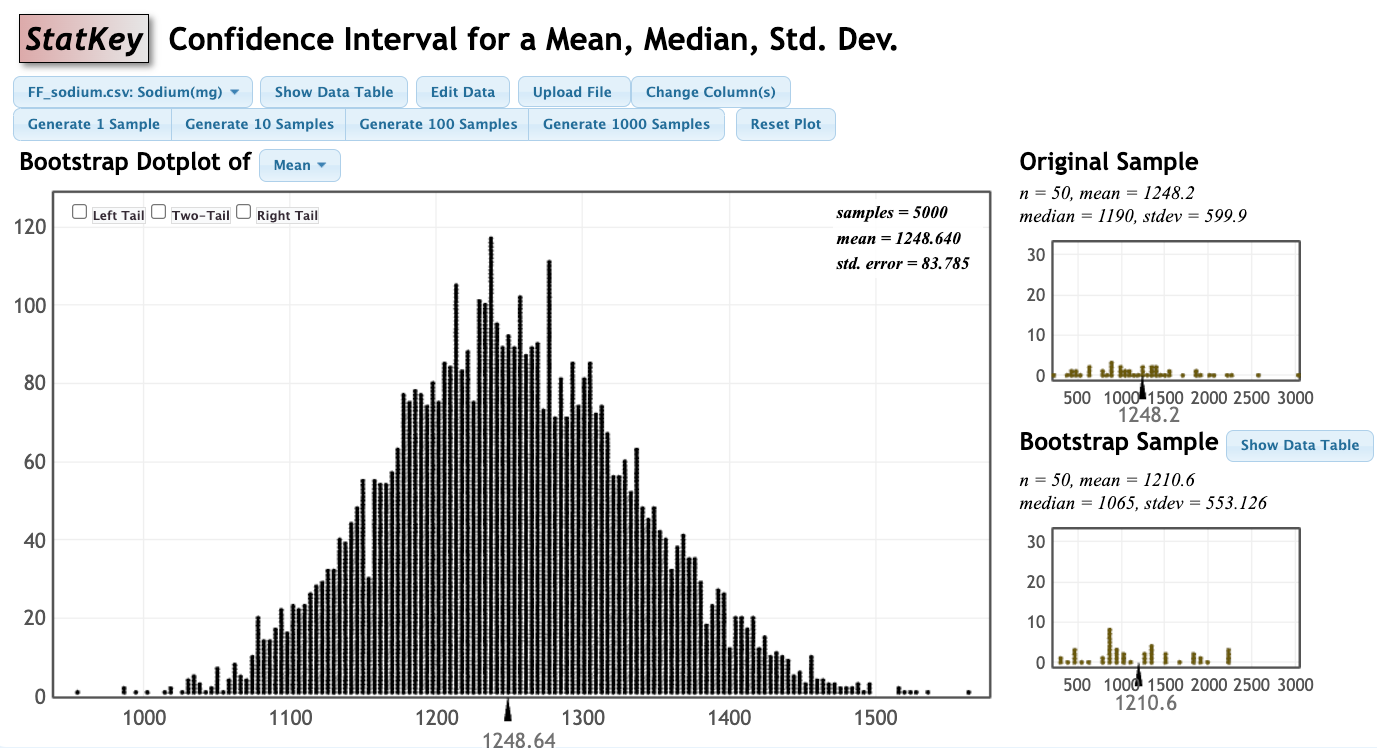
- Check the "Two-Tail" box at the upper left corner of the bootstrap dotplot. By default, this will give you a 95% confidence interval. Select the 0.95 box in the middle and change to 0.90 to display the 90% interval.
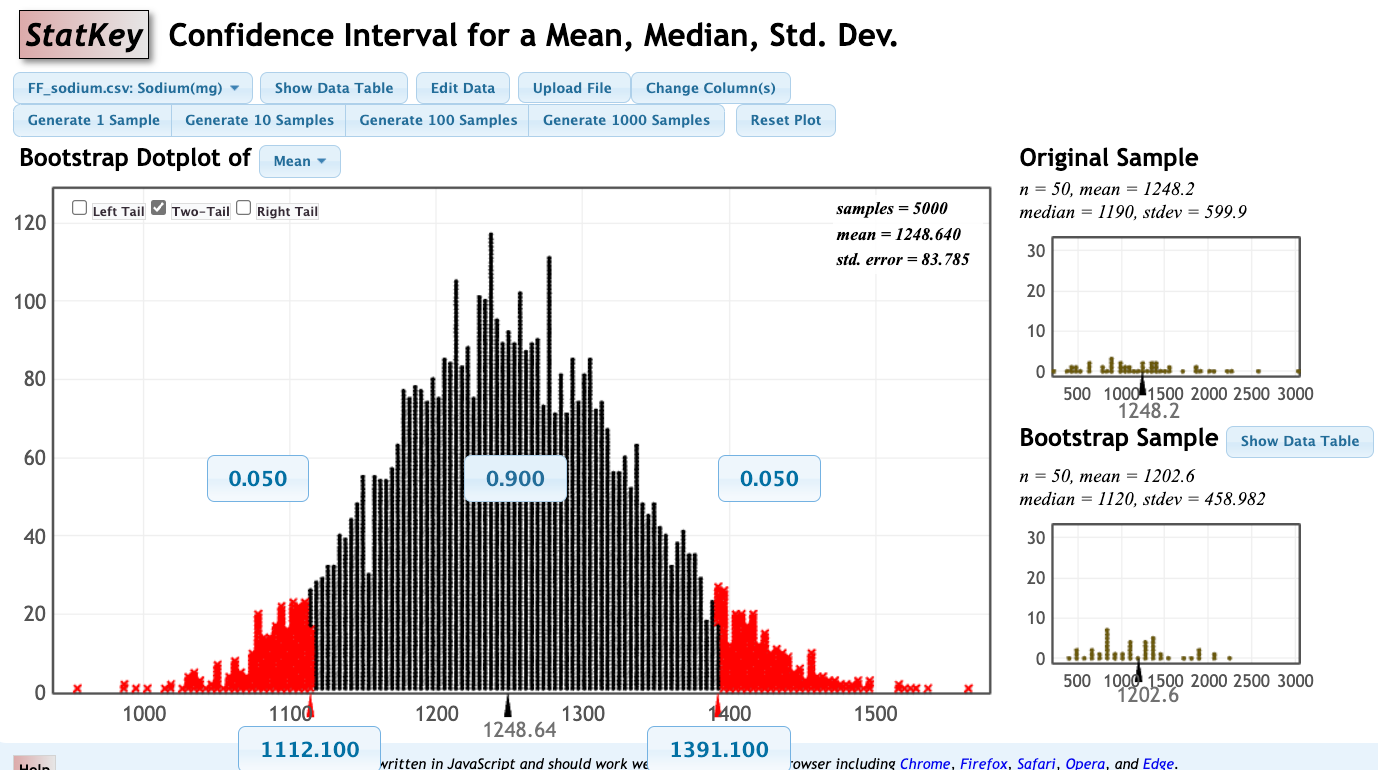
The 90% confidence interval for the average sodium content (mg) of a single fast food item is 1112.1 to 1391.1 mg.
4.5 - Paired Samples
4.5 - Paired SamplesIn Lesson 1 we learned about independent samples and paired samples. When we have two independent samples, the observations in the two groups are unrelated to one another and are not matched in any meaningful way. With paired samples, the observations in the two groups are matched in a meaningful way. Most often this occurs when data are collected twice from the same participants, such as in a pre-test / post-test design. But, there could be different participants in each group who are paired together meaningfully, such as brother-sister pairs or husband-wife pairs.
When data are paired, we compute the difference for each case, and then treat those differences as if they are a single measure. When constructing a confidence interval for the difference in paired means, we're really constructing a confidence interval for a single mean, where the single mean is the mean difference.
The population parameter is \(\mu_d\) where \(\mu_d=\mu_1-\mu_2\). The sample statistic is \(\overline x_d\) where \(\overline x_d = \overline x_1 - \overline x_2\).
Example
Research question: On average, how different are students' predicted exam scores and their actual exam scores?
4.6 - Impact of Sample Size on Confidence Intervals
4.6 - Impact of Sample Size on Confidence IntervalsEarlier in this lesson we learned that the sampling distribution is impacted by sample size. As the sample size increases the standard error decreases. With a larger sample size there is less variation between sample statistics, or in this case bootstrap statistics. Let's look at how this impacts a confidence interval.
Example: Proportion of Dog Owners
Below are two bootstrap distributions with 95% confidence intervals. In both examples \(\widehat p = 0.60\). However, the sample sizes are different.
In a sample of 20 World Campus students 12 owned a dog. StatKey was used to construct a 95% confidence interval using the percentile method:
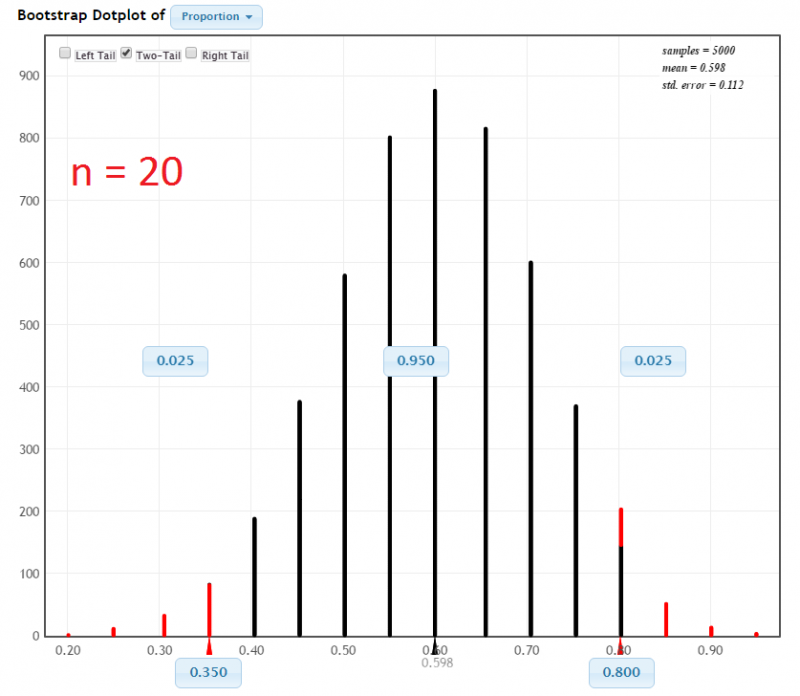
In a sample of 200 World Campus students, 120 owned a dog. StatKey was used to construct a 95% confidence interval using the percentile method:
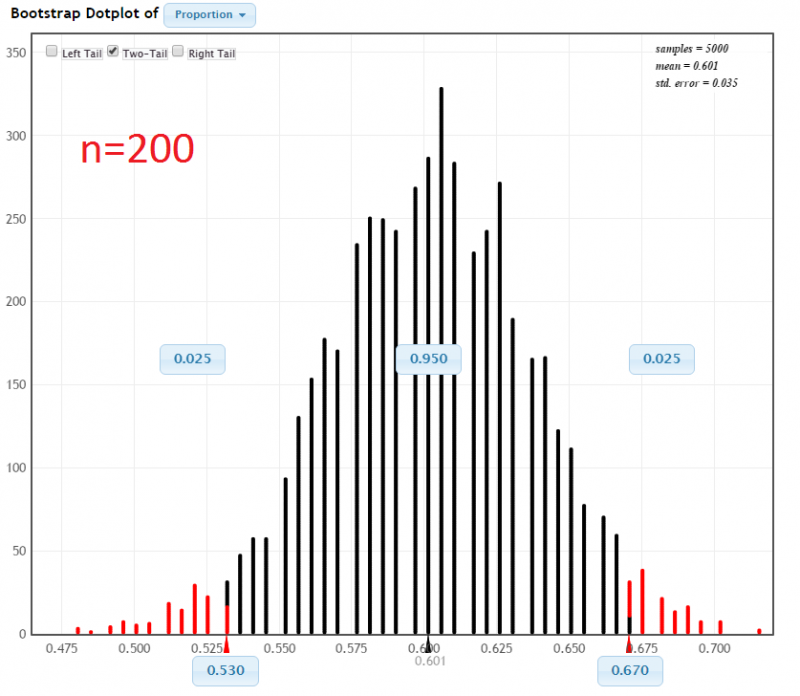
In each of the examples the proportion of dog owners was \(\widehat p = 0.60\). The difference was the sample size. When the sample size was increased from 20 to 200 the confidence interval became more narrow: from [0.350, 0.800] to [0.530, 0.670].
4.7 - Lesson 4 Summary
4.7 - Lesson 4 SummaryObjectives
- Construct and interpret sampling distributions using StatKey
- Explain the general form of a confidence interval
- Interpret a confidence interval
- Explain the process of bootstrapping
- Construct bootstrap confidence intervals using the standard error method
- Construct bootstrap confidence intervals using the percentile method in StatKey
- Construct bootstrap confidence intervals using Minitab
- Describe how sample size impacts a confidence interval
As you work through the textbook reading and assignments this week you may want to have a copy of the table below. One of the biggest challenges students often face in this lesson is being able to select the correct procedure. Whether you're constructing a confidence interval for a single mean, single proportion, single proportion, etc., depends on what type of variable or variables you are working with. You may want to return to the earlier lessons to review categorical and quantitative variables.
| Population Parameter | Sample Statistic | |
|---|---|---|
| Single mean | \(\mu\) | \(\overline x\) |
| Difference in two independent means | \(\mu_1 - \mu_2\) | \(\overline x_1 - \overline x_2\) |
| Single proportion | \(p\) | \(\widehat p\) |
| Difference in two proportions | \(p_1 - p_2\) | \(\widehat p_1 - \widehat p_2\) |
| Correlation | \(\rho\) | \(r\) |
| Slope (simple linear regression) | \(\beta\) | \(b\) |
Note: In this lesson we also learned how to construct a confidence interval for the difference in paired means. We use this procedure when each case (i.e., participant) has two observations and we want to estimate the average difference. In this case, the population parameter is \(\mu_d\) and the observed sample statistic is \(\overline x_d\). This is treated as a single sample mean test where the variable that we're working with is the difference.