8.2.2.1.3 - Example: Milk
8.2.2.1.3 - Example: MilkA study of 66,831 dairy cows found that the mean milk yield was 12.5 kg per milking with a standard deviation of 4.3 kg per milking (data from Berry, et al., 2013). Construct a 95% confidence interval for the average milk yield in the population.
First, let's compute the standard error:
\(SE=\dfrac{s}{\sqrt{n}}=\dfrac{4.3}{\sqrt{66831}}=0.0166\)
The standard error is small because the sample size is very large.
Next, let's find the \(t^*\) multiplier:
\(df=66831-1=66830\)
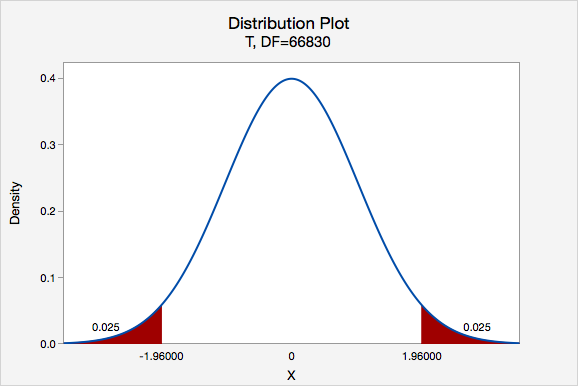
\(t^{*}=1.960\)
Now, we can construct our 95% confidence interval:
95% C.I.: \(12.5\pm1.960(0.017)=12.5\pm0.033=[12.467,\;12.533]\)
We are 95% confident that the mean milk yield in the population is between 12.467 and 12.533 kg per milking.