9.1.2.1.2 – Example: Same Sex Marriage
9.1.2.1.2 – Example: Same Sex MarriageExample: Same Sex Marriage
A survey was given to a random sample of college students. They were asked whether they think same sex marriage should be legal. We're going to compare the students who identified as women and men in terms of whether or not they responded "yes" to this question. Of the 251 women in the sample, 185 said "yes." Of the 199 men in the sample, 107 said "yes."
For women, there were 185 who said "yes" and 66 who said "no." For men, there were 107 who said "yes" and 92 who said "no." There are at least 10 successes and failures in each group so the normal approximation method can be used.
\(\widehat{p}_{w}=\dfrac{185}{251}\)
\(\widehat{p}_{m}=\dfrac{107}{199}\)
This is a two-tailed test because we are looking for a difference between women and men, we were not given a specific direction.
- \( H_{0} : p_{w}- p_{m}=0 \)
- \( H_{a} : p_{w}- p_{m}\neq 0 \)
\(\widehat{p}=\dfrac{185+107}{251+199}=\dfrac{292}{450}=0.6489\)
\(SE_0=\sqrt{\frac{292}{450}\left ( 1-\frac{292}{450} \right )\left ( \frac{1}{251}+\frac{1}{199} \right )}=0.0453\)
\(z=\dfrac{\frac{185}{251}-\frac{107}{199}}{0.0453}=4.400\)
Our test statistic is \(z=4.400\)
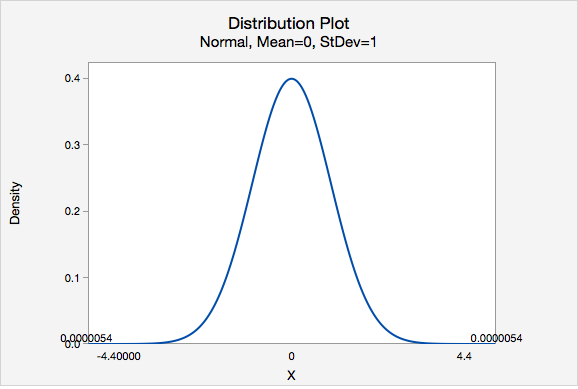
\(P(z>4.400)=0.0000054\), this is a two-tailed test, so this value must be multiplied by two: \(0.0000054\times 2= 0.0000108\)
\(p<0.0001\)
\(p\leq0.05\), therefore we reject the null hypothesis.
There is evidence, in this population of students, that there is a difference between the proportion of women and men who think that same sex marriage should be legal.