11.2.1.3 - Roulette Wheel (Different Proportions)
11.2.1.3 - Roulette Wheel (Different Proportions)Example: Roulette Wheel
Research Question: An American roulette wheel contains 38 slots: 18 red, 18 black, and 2 green. A casino has purchased a new wheel and they want to know if there is any evidence that the wheel is unfair. They spin the wheel 100 times and it lands on red 44 times, black 49 times, and green 7 times.
If the wheel is fair then \(p_{red}=\dfrac{18}{38}\), \(p_{black}=\dfrac{18}{38}\), and \(p_{green}=\dfrac{2}{38}\).
All of these proportions combined equal 1.
\(H_0: p_{red}=\dfrac{18}{38},\;p_{black}=\dfrac{18}{38}\;and\;p_{green}=\dfrac{2}{38}\)
\(H_a: At\;least\;one\;p_i\;is \;not\;as\;specified\;in\;the\;null\)
In order to conduct a chi-square goodness of fit test all expected values must be at least 5.
For both red and black: \(Expected \;count=100(\dfrac{18}{38})=47.368\)
For green: \(Expected\;count=100(\dfrac{2}{38})=5.263\)
All expected counts are at least 5 so we can conduct a chi-square goodness of fit test.
\(\chi^2=\sum \dfrac{(Observed-Expected)^2}{Expected} \)
In the first step we computed the expected values for red and black to be 47.368 and for green to be 5.263.
\(\chi^2= \dfrac{(44-47.368)^2}{47.368}+\dfrac{(49-47.368)^2}{47.368}+\dfrac{(7-5.263)^2}{5.263} \)
\(\chi^2=0.239+0.056+0.573=0.868\)
Our sampling distribution will be a chi-square distribution.
\(df=k-1=3-1=2\)
We can find the p-value by constructing a chi-square distribution with 2 degrees of freedom to find the area to the right of \(\chi^2=0.868\)
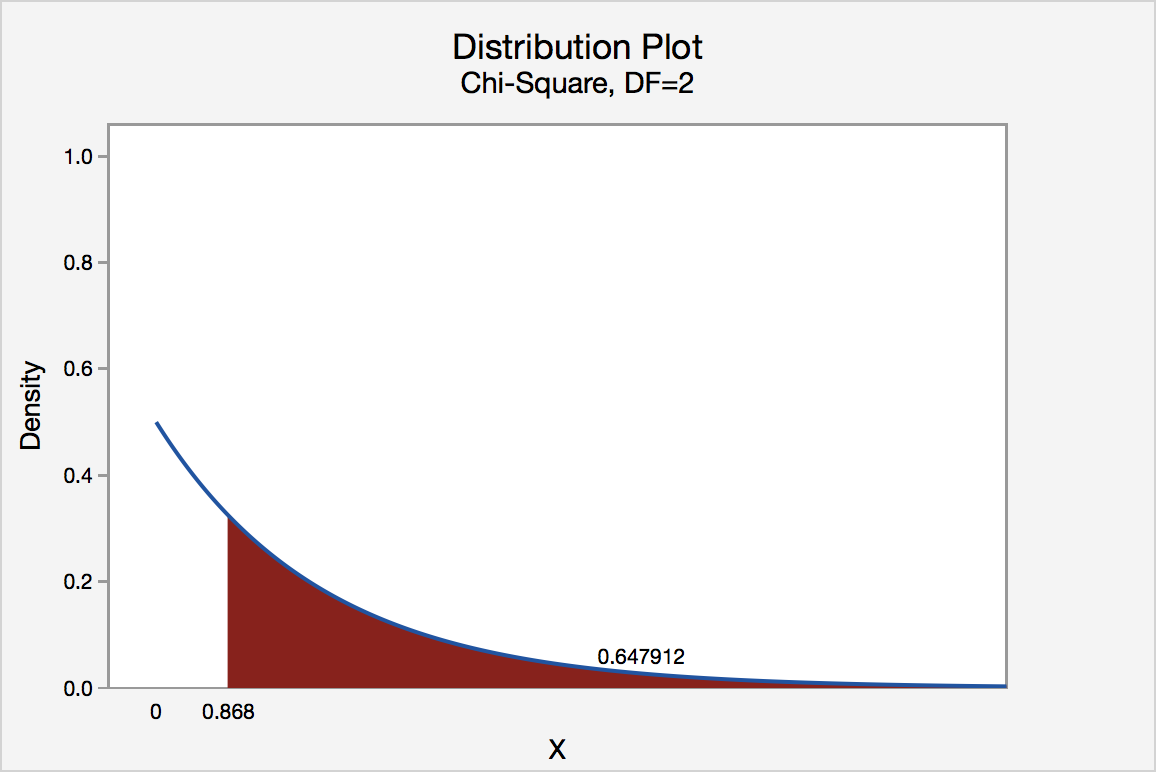
The p-value is 0.647912
\(p>0.05\) therefore we should fail to reject the null hypothesis.
There is not enough evidence that this roulette wheel is unfair.