Section 3: Continuous Distributions
Section 3: Continuous DistributionsIn the previous section, we investigated probability distributions of discrete random variables, that is, random variables whose support \(S\), contains a countable number of outcomes. In the discrete case, the number of outcomes in the support \(S\) can be either finite or countably infinite. In this section, as the title suggests, we are going to investigate probability distributions of continuous random variables, that is, random variables whose support \(S\) contains an infinite interval of possible outcomes.
You'll definitely want to make sure your calculus skills of integration and differentiation are up to snuff before tackling many of the problems you'll encounter in this section.
Lesson 13: Exploring Continuous Data
Lesson 13: Exploring Continuous DataOverview

In the beginning of this course (in the very first lesson!), we learned how to distinguish between discrete and continuous data. Discrete data are, again, data with a finite or countably infinite number of possible outcomes. Continuous data, on the other hand, are data which come from an interval of possible outcomes. Examples of discrete data include the number of siblings a randomly selected person has, the total on the faces of a pair of six-sided dice, and the number of students you need to ask before you find one who loves Stat 414. Examples of continuous data include:
- the amount of rain, in inches, that falls in a randomly selected storm
- the weight, in pounds, of a randomly selected student
- the square footage of a randomly selected three-bedroom house
In each of these examples, the resulting measurement comes from an interval of possible outcomes. Recall that the measurement tool is often the restricting factor with continuous data. That is, if I say I weigh 120 pounds, I don't actually weigh exactly 120 pounds... that's just what my scale tells me. In reality, I might weigh 120.01284027401307 pounds... that's where the interval of possible outcomes comes in. That is, the possible measurements cannot be put into one-to-one correspondence with the integers.
In this lesson, we'll investigate (or in some cases, review?) ways of summarizing continuous data. We'll summarize the data graphically using histograms, stem-and-leaf plots, and box plots. We've already discussed a couple of ways of summarizing continuous data numerically via the sample mean and sample variance. Here, we'll investigate how to summarize continuous data numerically using order statistics and various functions of order statistics.
One more thing here.... we'll be learning how to summarize data by hand. In reality, you would rarely rarely rarely ever do that in practice. Maybe if you were stranded on a desert island? In reality, 999 times out of a 1000, you and I are going to use statistical software to calculate percentiles and to create histograms, stem-and-leaf plots, and box plots. What's important here is that you just get the idea of how such graphs are created and such statistics are calculated, so that you know what they tell you when you encounter them.
Objectives
- To learn how to create and read a histogram.
- To learn and be able to apply the empirical rule to a set of data.
- To learn how to create and read a stem-and-leaf plot.
- To learn how to create and read a box plot.
- To learn how to use order statistics to determine sample percentiles.
- To learn how to calculate the five-number summary for a set of data.
13.1 - Histograms
13.1 - HistogramsExample 13-1
The material on this page should look awfully familiar as we briefly investigated histograms in the first lesson of the course. We review them again briefly here.
The following numbers are the measured nose lengths (in millimeters) of 60 students:
| 38 | 50 | 38 | 40 | 35 | 32 | 45 | 50 | 40 | 32 | 40 | 47 | 70 | 55 | 51 |
| 43 | 40 | 45 | 45 | 55 | 37 | 50 | 45 | 45 | 55 | 50 | 45 | 35 | 52 | 32 |
| 45 | 50 | 40 | 40 | 50 | 41 | 41 | 40 | 40 | 46 | 45 | 40 | 43 | 45 | 42 |
| 45 | 45 | 48 | 45 | 45 | 35 | 45 | 45 | 40 | 45 | 40 | 40 | 45 | 35 | 52 |
Recall that although the numbers look discrete, they are technically continuous. The measuring tools, which consisted of a piece of string and a ruler, were the limiting factors in getting more refined measurements. In most cases, it appears as if nose lengths come in five-millimeter increments... 35, 40, 45, 55... but that's, again, just measurement error. In order to create a histogram of these continuous measurements, we will use the following guidelines.
To create a histogram of continuous data
First, you have to group the data into a set of classes, typically of equal length. There are many, many sets of rules for defining the classes. For our purposes, we'll just rely on our common sense — having too few classes is as bad as having too many.
- Determine the number, \(n\), in the sample.
- Define \(k\) class intervals \((c_0, c_1], (c_1, c_2], \ldots, (c_{k-1}, c_k]\) .
- Determine the frequency, \(f_i\), of each class \(i\).
- Calculate the relative frequency (proportion) of each class by dividing the class frequency by the total number in the sample — that is, \(\frac{f_i}{n}\).
- For a frequency histogram: draw a rectangle for each class with the class interval as the base and the height equal to the frequency of the class.
- For a relative frequency histogram: draw a rectangle for each class with the class interval as the base and the height equal to the relative frequency of the class.
- For a density histogram: draw a rectangle for each class with the class interval as the base and the height equal to \(h(x)=\dfrac{f_i}{n(c_i-c_{i-1})}\)
Example 13-1 Continued
Here's what the work would like for our nose length example if we used 5 mm classes centered at 30, 35, ... 70:
| Class Interval | Tally | Frequency | Relative Frequency | Density Height |
|---|---|---|---|---|
| 27.5-32.5 | || | 2 | 0.033 | 0.0066 |
| 32.5-37.5 | ||||| | 5 | 0.083 | 0.0166 |
| 37.5-42.5 | ||||| ||||| ||||| || | 17 | 0.283 | 0.0566 |
| 42.5-47.5 | ||||| ||||| ||||| ||||| | | 21 | 0.350 | 0.0700 |
| 47.5-52.5 | ||||| ||||| | | 11 | 0.183 | 0.0366 |
| 52.5-57.5 | ||| | 3 | 0.183 | 0.0366 |
| 57.5-62.5 | 0 | 0 | 0 | |
| 62.5-67.5 | 0 | 0 | 0 | |
| 67.5-72.5 | | | 1 | 0.017 | 0.0034 |
| 60 | 0.999 (rounding) |
And, here is what the density histogram would like:
Note that a density histogram is just a modified relative frequency histogram. A density histogram is defined so that:
- the area of each rectangle equals the relative frequency of the corresponding class, and
- the area of the entire histogram equals 1.
Empirical Rule
We've previously learned that the sample mean can be thought of as the "center" of a set of data, while the sample standard deviation indicates "how spread out" the data are from the sample mean. Now, if a histogram is "mound-shaped" or "bell-shaped," then we can use the sample mean, sample standard deviation, and what is called the Empirical Rule to determine three intervals for which we would expect approximately 68%, 95%, and 99.7% of the data to fall.
The Empirical Rule tells us that if a histogram is at least approximately bell-shaped, then:
- Approximately 68% of the data are in the interval:
\((\bar{x}-s,\bar{x}+s)\)
- Approximately 95% of the data are in the interval:
\((\bar{x}-2s,\bar{x}+2s)\)
- Approximately 99.7% of the data are in the interval:
\((\bar{x}-3s,\bar{x}+3s)\)
Example 13-2
The federal government's average income from federal income taxes (on a per capita basis) for each of the 50 states in fiscal year 1991 is \$1252.44 with a standard deviation of \$393.75. Assuming the data are approximately bell-shaped, use the Empirical Rule to determine three intervals for which we would expect approximately 68%, 95%, and 99.7% of the data to fall.
Solution
The Empirical Rule tells us that we can expect 68% of the per capita taxes to fall between:
\(\bar{x}-s=\$ 1252.44-\$ 393.75=\$ 858.69\) and \(\bar{x}+s=\$ 1252.44+\$ 393.75=\$ 1646.19\)
The Empirical Rule also tells us that we can expect 95% of the per capita taxes to fall between:
\(\bar{x}-2s=\$ 1252.44-2(\$ 393.75)=\$ 464.94\) and \(\bar{x}+2s=\$ 1252.44+2(\$ 393.75)=\$ 2039.94\)
The Empirical Rule also tells us that we can expect 99.7% (virtually all!) of the per capita taxes to fall between:
\(\bar{x}-3s=\$ 1252.44-3(\$ 393.75)=\$ 71.19\) and \(\bar{x}+3s=\$ 1252.44+3(\$ 393.75)=\$ 2433.69\)
13.2 - Stem-and-Leaf Plots
13.2 - Stem-and-Leaf PlotsExample 13-3
A random sample of 64 people were selected to take the Stanford-Binet Intelligence Test. After each person completed the test, they were assigned an intelligence quotient (IQ) based on their performance on the test. The resulting 64 IQs are as follows:
| 111 | 85 | 83 | 98 | 107 | 101 | 100 | 94 | 101 | 86 |
| 105 | 122 | 104 | 106 | 90 | 123 | 102 | 107 | 93 | 109 |
| 141 | 86 | 91 | 88 | 98 | 128 | 93 | 114 | 87 | 116 |
| 99 | 94 | 94 | 406 | 436 | 402 | 75 | 96 | 78 | 116 |
| 107 | 106 | 68 | 104 | 91 | 87 | 105 | 97 | 110 | 91 |
| 107 | 107 | 85 | 117 | 93 | 108 | 91 | 110 | 105 | 99 |
| 85 | 99 | 99 | 96 |
Once the data are obtained, it might be nice to summarize the data. We could, of course, summarize the data using a histogram. One primary disadvantage of using a histogram to summarize data is that the original data aren't preserved in the graph. A stem-and-leaf plot, on the other hand, summarizes the data and preserves the data at the same time.
The basic idea behind a stem-and-leaf plot is to divide each data point into a stem and a leaf. We could divide our first data point, 111, for example, into a stem of 11 and a leaf of 1. We could divide 85 into a stem of 8 and a leaf of 5. We could divide 83 into a stem of 8 and a leaf of 3. And so on. To create the plot then, we first create a column of numbers containing the ordered stems. Our IQ data set produces stems 6, 7, 8, 9, 10, 11, 12, 13, and 14. Once the column of stems are written down, we work our way through each number in the data set, and write its leaf in the row headed by its stem.
Here's what the our stem-and-leaf plot would look like after adding the first five numbers 111, 85, 83, 98, and 107:
| 6 | |
|---|---|
| 7 | |
| 8 | 53 |
| 9 | 8 |
| 10 | 7 |
| 11 | 1 |
| 12 | |
| 13 | |
| 14 |
and here's what the completed stem-and-leaf plot would look like after adding all 64 leaves to the nine stems:
| 6 | 8 |
|---|---|
| 7 | 58 |
| 8 | 536687755 |
| 9 | 84031839446171319996 |
| 10 | 71015462796276457785 |
| 11 | 1466070 |
| 12 | 238 |
| 13 | 6 |
| 14 | 1 |
Now, rather than looking at a list of 64 unordered IQs, we have a nice picture of the data that quite readily tells us that:
- the distribution of IQs is bell-shaped
- most of the IQs are in the 90s and 100s
- the smallest IQ in the data set is 68, while the largest is 141
That's all well and good, but we could do better. First and foremost, no one in their right mind is going to want to create too many of these stem-and-leaf plots by hand. Instead, you'd probably want to let some statistical software, such as Minitab or SAS, do the work for you. Here's what Minitab's stem-and-leaf plot of the 64 IQs looks like:
| Stem-and-Leaf of IQ | N=64 | |
|---|---|---|
| Leaf Unit = 1.0 | ||
| 1 | 6 | 8 |
| 1 | 6 | 8 |
| 1 | 7 | |
| 3 | 7 | 58 |
| 4 | 8 | 3 |
| 12 | 8 | 55566778 |
| 23 | 9 | 01111333444 |
| 32 | 9 | 667889999 |
| 32 | 10 | 0112244 |
| 25 | 10 | 5556667777789 |
| 12 | 11 | 0014 |
| 8 | 11 | 667 |
| 5 | 12 | 23 |
| 3 | 12 | 8 |
| 2 | 13 | 6 |
| 1 | 14 | 1 |
Hmmm.... how does the plot differ from ours? First, Minitab tells us that there are n = 64 numbers and that the leaf unit is 1.0. Then, ignoring the first column of numbers for now, the second column contains the stems from 6 to 14. Note, though, that Minitab uses two rows for each of the stems 7, 8, 9, 10, 11, 12, and 13. Minitab takes an alternative here that we could have taken as well. When you opt to use two rows for each stem, the first row is reserved for the leaves 0, 1, 2, 3, and 4, while the second row is reserved for the leaves 5, 6, 7, 8, and 9. For example, note that the first 9 row contains the 0 to 4 leaves, while the second 9 row contains the 5 to 9 leaves. The decision to use one or two rows for the stems depends on the data. Sometimes the one row per stem option produces the better plot, and sometimes the two rows per stem plot option produces the better plot.
Do you notice any other differences between Minitab's plot and our plot? Note that the leaves in Minitab's plot are ordered. That's right... Minitab orders the data before producing the plot, and thereby creating what is called an ordered stem-and-leaf plot.
Now, back to that first column of numbers appearing in Minitab's plot. That column contains what are called depths. The depths are the frequencies accumulated from the top of the plot and the bottom of the plot until they converge in the middle. For example, the first number in the depths column is a 1. It comes from the fact that there is just one number in the first (6) stem. The second number in the depths column is also a 1. It comes from the fact that there is 1 leaf in the first (6) stem and 0 leaves in the second (the first 7) stem, and so 1 + 0 = 1. The third number in the depths column is a 3. It comes from the fact that there is 1 leaf in the first (6) stem, 0 leaves in the second (the first 7) stem, and 2 leaves in the third (the second 7) stem, and so 1 + 0 + 2 = 3. Minitab continues accumulating numbers down the column until it reaches 32 in the last 9 stem. Then, Minitab starts accumulating from the bottom of the plot. The 5 in the depths column comes, for example, from the fact that there is 1 leaf in the last (14) stem, 1 leaf in the second 13 stem, 0 leaves in the first 13 stem, 1 leaf in the second 12 stem, and 2 leaves in the first 12 stem, and so 1 + 1+ 0 + 1 + 2 = 5.
Let's take a look at another example.
Example 13-4
Let's consider a random sample of 20 concentrations of calcium carbonate (\(CaCO_3\)) in milligrams per liter.
| 130.8 | 129.9 | 131.5 | 131.2 | 129.5 | 132.7 | 131.5 | 127. | 133.7 |
| 132.2 | 134.8 | 131.7 | 133.9 | 129.8 | 131.4 | 12.8 | 132.7 | 132.8 |
| 131.4 | 131.3 |
Create a stem-and-leaf plot of the data.
Solution
Let's take the efficient route, as most anyone would likely be taken in practice, by letting Minitab generate the plot for us:

Minitab tells us that the leaf unit is 0.1, so that the stem of 127 and leaf of 8 represents the number 127.8. The depths column contains something a little different here, namely the 7 with parentheses around it. It seems that Minitab's algorithm for calculating the depths differs a bit here. It still accumulates the values from the top and the bottom, but it stops in each direction when it reaches the row containing the middle value (median) of the sample. The frequency of that row containing the median is simply placed in parentheses. That is, the median of the 20 numbers is 131.45. Therefore, because the 131 stem contains 7 leaves, the depths column for that row contains a 7 in parentheses.
In our previous example, the median of the 64 IQs is 99.5. Because 99.5 falls between two rows of the display, namely between the stems 99 and 100, Minitab calculates the depths instead as described in that example, and omits the whole "parentheses around the frequency of the median row" thing.
13.3 - Order Statistics and Sample Percentiles
13.3 - Order Statistics and Sample PercentilesThe primary advantage of creating an ordered stem-and-leaf plot is that you can readily read what are called the order statistics right off of the plot. If we have a sample of \(n\) observations represented as:
\(x_1,x_2,x_3,\cdots,x_n\)
then when the observations are ordered from smallest to largest, the resulting ordered data are called the order statistics of the sample, and are represented as:
\(y_1 \leq y_2 \leq y_3 \leq \cdots \leq y_n\)
That is, \(y_1\), the smallest data point is the first order statistic. The second smallest data point, \(y_2\), is the second order statistic. And so on, until we reach the largest data point and \(n^{th}\) order statistic, \(y_n\). From the order statistics, it is rather easy to find the sample percentiles.
Definition. If \(0<p<1\), then the \((100p)^{th}\) sample percentile has approximately \(np\) sample observations less than it, and \(n(1-p)\) sample observations greater than it.
Some sample percentiles have special names:
- The 25th percentile is also called the first quartile and is denoted as \(q_1\).
- The 50th percentile is also called the second quartile or median, and is denoted as \(q_2\) or \(m\).
- The 75th percentile is also called the third quartile and is denoted as \(q_3\).
Here's the typical method used for finding a particular sample percentile:
-
Arrange the sample data in increasing order. That is, determine the order statistics:
\(y_1 \leq y_2 \leq y_3 \leq \cdots \leq y_n\)
-
If \((n+1)p\) is an integer, then the \((100p)^{th}\) sample percentile is the \((n+1)p^{th}\) order statistic.
-
If \((n+1)p\) is not an integer, but rather equals \(r\) plus some proper fraction, \(a/b\) say, then use a weighted average of the \(r^{th}\) and \((r+1)^{st}\) order statistics. That is, define the \((100p)^{th}\) sample percentile as:
\(\tilde{\pi}_p=y_r+\left(\dfrac{a}{b}\right)(y_{r+1}-y_r)\)
Let's try this method out on an example or two.
Example 13-3 Revisited
Let's return to our random sample of 64 people selected to take the Stanford-Binet Intelligence Test. The resulting 64 IQs were sorted as follows:
| 68 | 75 | 78 | 83 | 85 | 85 | 85 | 86 | 86 | 87 |
| 84 | 88 | 90 | 91 | 91 | 91 | 91 | 93 | 93 | 93 |
| 94 | 94 | 94 | 96 | 96 | 97 | 98 | 98 | 99 | 99 |
| 99 | 99 | 100 | 101 | 101 | 102 | 102 | 104 | 104 | 105 |
| 105 | 105 | 106 | 106 | 106 | 107 | 107 | 107 | 107 | 107 |
| 108 | 109 | 110 | 110 | 111 | 114 | 116 | 116 | 117 | 122 |
| 123 | 128 | 136 | 141 |
That is, the first order statistic is \(y_1=68\), the second-order statistic is \(y_2=75\), and the \(64^{th}\) order statistic is \(y_{64}=141\). Find the 25th sample percentile, the 50th sample percentile, 75th sample percentile, and the interquartile range.
Solution
Here, we have \(n=64\) IQs. To find the 25th sample percentile, we need to consider \(p=0.25\). In that case:
\((n+1)p=(64+1)(0.25)=(65)(0.25)=16.25\)
Because 16.25 is not an integer, we are going to need to interpolate linearly between the 16th order statistic (91) and 17th order statistic (91). That is, the 25th sample percentile (or first quartile) is 91, as determined by:
\(\tilde{\pi}_{0.25}=y_{16}+(0.25)(y_{17}-y_{16})=91+0.25(91-91)=91\)
To find the 50th sample percentile, we need to consider \(p=0.50\). In that case:
\((n+1)p=(64+1)(0.5)=(65)(0.5)=32.5\)
Because 32.5 is not an integer, we are going to need to interpolate linearly between the 32nd order statistic (99)and 33rd order statistic (100). That is, the 50th sample percentile (or second quartile or median) is 99.5 as determined by:
\(\tilde{\pi}_{0.5}=y_{32}+(0.5)(y_{33}-y_{32})=99+0.5(100-99)=99.5\)
To find the 75th sample percentile, we need to consider \(p=0.75\). In that case:
\((n+1)p=(64+1)(0.75)=(65)(0.75)=48.75\)
Because 48.75 is not an integer, we are going to need to interpolate linearly between the 48th order statistic (107) and 49th order statistic (107). That is, the 75th sample percentile (or third quartile) is 107 as determined by:
\(\tilde{\pi}_{0.75}=y_{48}+(0.75)(y_{49}-y_{48})=107+0.75(107-107)=107\)
The interquartile range IQR is then 107−91 = 16.
Example 13-3 Revisited again
Let's return again to our IQ data, but this time suppose that the person deemed to have the largest IQ (141) couldn't take the pressure of the test and fainted before completing the test. In that case, the sorted data of the now \(n=63\) IQs look like this:
| 68 | 75 | 78 | 83 | 85 | 85 | 85 | 86 | 86 | 87 |
| 87 | 88 | 90 | 91 | 91 | 91 | 91 | 93 | 93 | 93 |
| 94 | 94 | 94 | 96 | 96 | 97 | 98 | 98 | 99 | 99 |
| 99 | 99 | 100 | 101 | 101 | 102 | 102 | 104 | 104 | 105 |
| 105 | 105 | 106 | 106 | 106 | 107 | 107 | 107 | 107 | 107 |
| 108 | 109 | 110 | 110 | 111 | 114 | 116 | 116 | 117 | 122 |
| 123 | 128 | 136 |
You should notice that the once largest observation (141) no longer exists in the data set. Find the 25th sample percentile, the 50th sample percentile, 75th sample percentile, and the interquartile range.
Solution
Here, we have \(n=63\) IQs. To find the 25th sample percentile, we need to consider \(p=0.25\). In that case:
\((n+1)p=(63+1)(0.25)=(64)(0.25)=16\)
Because 16 is an integer, the 25th sample percentile (or first quartile) is readily determined to be the 16th order statistic, that is, 91.
To find the 50th sample percentile, we need to consider \(p=0.50\). In that case:
\((n+1)p=(63+1)(0.5)=(64)(0.5)=32\)
Because 32 is an integer, the 50th sample percentile (or second quartile or median) is readily determined to be the 32nd order statistic, that is 99.
To find the 75th sample percentile, we need to consider \(p=0.75\). In that case:
\((n+1)p=(63+1)(0.75)=(64)(0.75)=48\)
Because 48 is an integer, the 75th sample percentile (or third quartile) is readily determined to be the 48th order statistic, that is, 107.
The interquartile range IQR is then again 107−91 = 16.
13.4 - Box Plots
13.4 - Box PlotsOn the last page, we learned how to determine the first quartile, the median, and the third quartile for a sample of data. These three percentiles, along with a data set's minimum and maximum values, make up what is called the five-number summary. One nice way of graphically depicting a data set's five-number summary is by way of a box plot (or box-and-whisker plot).
Here are some general guidelines for drawing a box plot:
- Draw a horizontal axis scaled to the data.
- Above the axis, draw a rectangular box with the left side of the box at the first quartile \(q_1\) and the right side of the box at the third quartile \(q_3\).
- Draw a vertical line connecting the lower and upper horizontal lines of the box at the median \(m\).
- For the left whisker, draw a horizontal line from the minimum value to the midpoint of the left side of the box.
- For the right whisker, draw a horizontal line from the maximum value to the midpoint of the right side of the box.
Drawn as such, a box plot does a nice job of dividing the data graphically into fourths. Note, for example, that the horizontal length of the box is the interquartile range IQR, the left whisker represents the first quarter of the data, and the right whisker represents the fourth quarter of the data.
Example 13-3 Revisited
Let's return to our random sample of 64 people selected to take the Stanford-Binet Intelligence Test. The resulting 64 IQs were sorted as follows:
| 68 | 75 | 78 | 83 | 85 | 85 | 85 | 86 | 86 | 87 |
| 87 | 88 | 90 | 91 | 91 | 91 | 91 | 93 | 93 | 93 |
| 94 | 94 | 94 | 96 | 96 | 97 | 98 | 98 | 99 | 99 |
| 99 | 99 | 100 | 101 | 101 | 102 | 102 | 104 | 104 | 105 |
| 105 | 105 | 106 | 106 | 106 | 107 | 107 | 107 | 107 | 107 |
| 108 | 109 | 110 | 110 | 111 | 114 | 116 | 116 | 117 | 122 |
| 123 | 128 | 136 | 141 |
We previously determined that the first quartile is 91, the median is 99.5, and the third quartile is 107. The interquartile range IQR is 16. Use these numbers, as well as the minimum value (68) and maximum value (141) to create a box plot of these data.
Solution
By following the guidelines given above, a hand-drawn box plot of these data looks something like this:
In reality, you will probably almost always want to use a statistical software package, such as Minitab, to create your box plots. If we ask Minitab to create a box plot for this data set, this is what we get:
Hmm. How come Minitab's box plot looks different than our box plot? Well, by default, Minitab creates what is called a modified box plot. In a modified box plot, the box is drawn just as in a standard box plot, but the whiskers are defined differently. For a modified box plot, the whiskers are the lines that extend from the left and right of the box to the adjacent values. The adjacent values are defined as the lowest and highest observations that are still inside the region defined by the following limits:
- Lower Limit: \(Q1-1.5\times IQR\)
- Upper Limit: \(Q3+1.5\times IQR\)
In this example, the lower limit is calculated as \(Q1-1.5\times IQR=91-1.5(16)=67\). Therefore, in this case, the lower adjacent value turns out to be the same as the minimum value, 68, because 68 is the lowest observation still inside the region defined by the lower bound of 67. Now, the upper limit is calculated as \(Q3+1.5\times IQR=107+1.5(16)=131\). Therefore, the upper adjacent value is 128, because 128 is the highest observation still inside the region defined by the upper bound of 131. In general, values that fall outside of the adjacent value region are deemed outliers. In this case, the IQs of 136 and 141 are greater than the upper adjacent value and are thus deemed as outliers. In Minitab's modified box plots, outliers are identified using asterisks.
Example 13-4 Revisited
Let's return to the example in which we have a random sample of 20 concentrations of calcium carbonate (\(CaCO_3\)) in milligrams per liter:
| 130.8 | 129.9 | 131.5 | 131.2 | 129.5 | 132.7 | 131.5 | 127.8 | 133.7 |
| 132.2 | 134.8 | 131.7 | 133.9 | 129.8 | 131.4 | 128.8 | 132.7 | 132.8 |
| 131.4 | 131.3 |
With a little bit of work, it can be shown that the five-number summary is as follows:
- Minimum: 127.8
- First quartile: 130.12
- Median: 131.45
- Third quartile: 132.70
- Maximum: 134.8
Use the five-number summary to create a box plot of these data.
Solution
By following the guidelines given above, a hand-drawn box plot of these data looks something like this:
In this case, the interquartile range IQR \(132.7-130.12-2.58\). Therefore, the lower limit is calculated as \(Q1-1.5\times IQR=130.12-1.5(2.58)=126.25\). Therefore, the lower adjacent value is the same as the minimum value, 127.8, because 127.8 is lowest observation still inside the region defined by the lower bound of 126.25. The upper limit is calculated as \(Q3+1.5\times IQR=132.7+1.5(2.58)=136.57\). Therefore, the upper adjacent value is the same as the maximum value, 134.8, because 134.8 is the highest observation still inside the region defined by the upper bound of 136.57. Because the lower and upper adjacent values are the same as the minimum and maximum values, respectively, the box plot looks the same as the modified box plot
13.5 - Shapes of distributions
13.5 - Shapes of distributionsHistograms and box plots can be quite useful in suggesting the shape of a probability distribution. Here, we'll concern ourselves with three possible shapes: symmetric, skewed left, or skewed right.
- Skewed Left
- For a distribution that is skewed left, the bulk of the data values (including the median) lie to the right of the mean, and there is a long tail on the left side.
- Skewed Right
- For a distribution that is skewed right, the bulk of the data values (including the median) lie to the left of the mean, and there is a long tail on the right side.
- Symmetric
- For a distribution that is symmetric, approximately half of the data values lie to the left of the mean, and approximately half of the data values lie to the right of the mean.
The following examples probably illustrate symmetry and skewness of distributions better than any formal definitions can.
Example 13-5
Consider a random sample of weights (in pounds) of 40 female college students:
| 135 | 117 | 137 | 135 | 133 | 145 | 129 | 157 | 113 | 134 |
| 144 | 141 | 132 | 138 | 133 | 134 | 132 | 135 | 152 | 141 |
| 140 | 119 | 138 | 136 | 156 | 141 | 116 | 131 | 138 | 128 |
| 120 | 148 | 130 | 140 | 121 | 137 | 121 | 145 | 145 | 125 |
Do these data suggest that the distribution of female weights is symmetric, skewed right, or skewed left?
Solution
The histogram:
and box plot of the 40 weights:
suggest that the distribution of female weights is symmetric.
Example 13-6
Consider a random sample of 26 grades on an easy statistics exam:
| 100 | 100 | 99 | 98 | 97 | 96 | 95 | 95 | 95 | 94 |
| 93 | 93 | 92 | 92 | 91 | 90 | 90 | 90 | 89 | 84 |
| 80 | 75 | 68 | 65 | 50 | 45 |
Do these data suggest that the distribution of exam scores is symmetric, skewed right, or skewed left?
Solution
The histogram:
and box plot of the 26 grades:
suggest that the distribution of easy exam scores is skewed to the left.
Example 13-7
Consider the lifetimes (in years) of a random sample of 39 Energizer bunnies:
| 0.2 | 3.6 | 3.1 | 0.9 | 0.7 | 7.8 | 1.4 | 0.4 | 3.1 | 3.4 |
| 5.3 | 3.2 | 0.3 | 3.1 | 6.0 | 2.8 | 5.6 | 0.2 | 1.4 | 0.9 |
| 2.4 | 0.8 | 1.8 | 1.0 | 2.9 | 0.5 | 0.9 | 3.2 | 1.3 | 11.1 |
| 0.8 | 1.8 | 1.4 | 0.2 | 1.0 | 1.1 | 1.6 | 0.7 | 3.2 |
Do these data suggest that the distribution of lifetimes of Energizer bunnies is symmetric, skewed right, or skewed left?
Solution
The histogram:
and box plot of the lifetimes of 39 Energizer bunnies:
suggest that the distribution of lifetimes of Energizer bunnies is skewed to the right.
Lesson 14: Continuous Random Variables
Lesson 14: Continuous Random VariablesOverview
A continuous random variable differs from a discrete random variable in that it takes on an uncountably infinite number of possible outcomes. For example, if we let \(X\) denote the height (in meters) of a randomly selected maple tree, then \(X\) is a continuous random variable. In this lesson, we'll extend much of what we learned about discrete random variables to the case in which a random variable is continuous. Our specific goals include:
- Finding the probability that \(X\) falls in some interval, that is finding \(P(a<X<b)\), where \(a\) and \(b\) are some constants. We'll do this by using \(f(x)\), the probability density function ("p.d.f.") of \(X\), and \(F(x)\), the cumulative distribution function ("c.d.f.") of \(X\).
- Finding the mean \(\mu\), variance \(\sigma^2\), and standard deviation of \(X\). We'll do this through the definitions \(E(X)\) and \(\text{Var}(X)\) extended for a continuous random variable, as well as through the moment generating function \(M(t)\) extended for a continuous random variable.
Objectives
- To introduce the concept of a probability density function of a continuous random variable.
- To learn the formal definition of a probability density function of a continuous random variable.
- To learn that if \(X\) is continuous, the probability that \(X\) takes on any specific value \(x\) is 0.
- To learn how to find the probability that a continuous random variable \(X\) falls in some interval \((a, b)\).
- To learn the formal definition of a cumulative distribution function of a continuous random variable.
- To learn how to find the cumulative distribution function of a continuous random variable \(X\) from the probability density function of \(X\).
- To learn the formal definition of a \((100p)^{th}\) percentile.
- To learn the formal definition of the median, first quartile, and third quartile.
- To learn how to use the probability density function to find the \((100p)^{th}\) percentile of a continuous random variable \(X\).
- To extend the definitions of the mean, variance, standard deviation, and moment-generating function for a continuous random variable \(X\).
- To be able to apply the methods learned in the lesson to new problems.
- To learn a formal definition of the probability density function of a continuous uniform random variable.
- To learn a formal definition of the cumulative distribution function of a continuous uniform random variable.
- To learn key properties of a continuous uniform random variable, such as the mean, variance, and moment generating function.
- To understand and be able to create a quantile-quantile (q-q) plot.
- To understand how randomly-generated uniform (0,1) numbers can be used to randomly assign experimental units to treatment.
- To understand how randomly-generated uniform (0,1) numbers can be used to randomly select participants for a survey.
14.1 - Probability Density Functions
14.1 - Probability Density FunctionsA continuous random variable takes on an uncountably infinite number of possible values. For a discrete random variable \(X\) that takes on a finite or countably infinite number of possible values, we determined \(P(X=x)\) for all of the possible values of \(X\), and called it the probability mass function ("p.m.f."). For continuous random variables, as we shall soon see, the probability that \(X\) takes on any particular value \(x\) is 0. That is, finding \(P(X=x)\) for a continuous random variable \(X\) is not going to work. Instead, we'll need to find the probability that \(X\) falls in some interval \((a, b)\), that is, we'll need to find \(P(a<X<b)\). We'll do that using a probability density function ("p.d.f."). We'll first motivate a p.d.f. with an example, and then we'll formally define it.
Example 14-1

Even though a fast-food chain might advertise a hamburger as weighing a quarter-pound, you can well imagine that it is not exactly 0.25 pounds. One randomly selected hamburger might weigh 0.23 pounds while another might weigh 0.27 pounds. What is the probability that a randomly selected hamburger weighs between 0.20 and 0.30 pounds? That is, if we let \(X\) denote the weight of a randomly selected quarter-pound hamburger in pounds, what is \(P(0.20<X<0.30)\)?
Solution
In reality, I'm not particularly interested in using this example just so that you'll know whether or not you've been ripped off the next time you order a hamburger! Instead, I'm interested in using the example to illustrate the idea behind a probability density function.
Now, you could imagine randomly selecting, let's say, 100 hamburgers advertised to weigh a quarter-pound. If you weighed the 100 hamburgers, and created a density histogram of the resulting weights, perhaps the histogram might look something like this:
In this case, the histogram illustrates that most of the sampled hamburgers do indeed weigh close to 0.25 pounds, but some are a bit more and some a bit less. Now, what if we decreased the length of the class interval on that density histogram? Then, the density histogram would look something like this:
Now, what if we pushed this further and decreased the intervals even more? You can imagine that the intervals would eventually get so small that we could represent the probability distribution of \(X\), not as a density histogram, but rather as a curve (by connecting the "dots" at the tops of the tiny tiny tiny rectangles) that, in this case, might look like this:
Such a curve is denoted \(f(x)\) and is called a (continuous) probability density function.
Now, you might recall that a density histogram is defined so that the area of each rectangle equals the relative frequency of the corresponding class, and the area of the entire histogram equals 1. That suggests then that finding the probability that a continuous random variable \(X\) falls in some interval of values involves finding the area under the curve \(f(x)\) sandwiched by the endpoints of the interval. In the case of this example, the probability that a randomly selected hamburger weighs between 0.20 and 0.30 pounds is then this area:
Now that we've motivated the idea behind a probability density function for a continuous random variable, let's now go and formally define it.
- Probability Density Function ("p.d.f.")
-
The probability density function ("p.d.f.") of a continuous random variable \(X\) with support \(S\) is an integrable function \(f(x)\) satisfying the following:
-
\(f(x)\) is positive everywhere in the support \(S\), that is, \(f(x)>0\), for all \(x\) in \(S\)
-
The area under the curve \(f(x)\) in the support \(S\) is 1, that is:
\(\int_S f(x)dx=1\)
-
If \(f(x)\) is the p.d.f. of \(x\), then the probability that \(x\) belongs to \(A\), where \(A\) is some interval, is given by the integral of \(f(x)\) over that interval, that is:
\(P(X \in A)=\int_A f(x)dx\)
-
As you can see, the definition for the p.d.f. of a continuous random variable differs from the definition for the p.m.f. of a discrete random variable by simply changing the summations that appeared in the discrete case to integrals in the continuous case. Let's test this definition out on an example.
Example 14-2
Let \(X\) be a continuous random variable whose probability density function is:
\(f(x)=3x^2, \qquad 0<x<1\)
First, note again that \(f(x)\ne P(X=x)\). For example, \(f(0.9)=3(0.9)^2=2.43\), which is clearly not a probability! In the continuous case, \(f(x)\) is instead the height of the curve at \(X=x\), so that the total area under the curve is 1. In the continuous case, it is areas under the curve that define the probabilities.
Now, let's first start by verifying that \(f(x)\) is a valid probability density function.
Solution
What is the probability that \(X\) falls between \(\frac{1}{2}\) and 1? That is, what is \(P\left(\frac{1}{2}<X<1\right)\)?
Solution
What is \(P\left(X=\frac{1}{2}\right)\)?
Solution
It is a straightforward integration to see that the probability is 0:
\(\int^{1/2}_{1/2} 3x^2dx=\left[x^3\right]^{x=1/2}_{x=1/2}=\dfrac{1}{8}-\dfrac{1}{8}=0\)
In fact, in general, if \(X\) is continuous, the probability that \(X\) takes on any specific value \(x\) is 0. That is, when \(X\) is continuous, \(P(X=x)=0\) for all \(x\) in the support.
An implication of the fact that \(P(X=x)=0\) for all \(x\) when \(X\) is continuous is that you can be careless about the endpoints of intervals when finding probabilities of continuous random variables. That is:
\(P(a\le X\le b)=P(a<X\le b)=P(a\le X<b)=P(a<x<b)\)
for any constants \(a\) and \(b\).
Example 14-3
Let \(X\) be a continuous random variable whose probability density function is:
\(f(x)=\dfrac{x^3}{4}\)
for an interval \(0<x<c\). What is the value of the constant \(c\) that makes \(f(x)\) a valid probability density function?
Solution
14.2 - Cumulative Distribution Functions
14.2 - Cumulative Distribution FunctionsYou might recall that the cumulative distribution function is defined for discrete random variables as:
\(F(x)=P(X\leq x)=\sum\limits_{t \leq x} f(t)\)
Again, \(F(x)\) accumulates all of the probability less than or equal to \(x\). The cumulative distribution function for continuous random variables is just a straightforward extension of that of the discrete case. All we need to do is replace the summation with an integral.
- Cumulative Distribution Function ("c.d.f.")
-
The cumulative distribution function ("c.d.f.") of a continuous random variable \(X\)is defined as:
\(F(x)=\int_{-\infty}^x f(t)dt\)
for \(-\infty<x<\infty\).
You might recall, for discrete random variables, that \(F(x)\) is, in general, a non-decreasing step function. For continuous random variables, \(F(x)\) is a non-decreasing continuous function.
Example 14-2 Revisited
Let's return to the example in which \(X\) has the following probability density function:
\(f(x)=3x^2, \qquad 0<x<1\)
What is the cumulative distribution function \(F(x)\)?
Example 14-3 Revisited again
Let's return to the example in which \(X\) has the following probability density function:
\(f(x)=\dfrac{x^3}{4}\)
for \(0<x<2\). What is the cumulative distribution function of \(X\)?
Example 14-4
Suppose the p.d.f. of a continuous random variable \(X\) is defined as:
\(f(x)=\begin{cases} x+1, & -1<x<0\\ 1-x, & 0\le x<1 \end{cases} \)
Find and graph the c.d.f. \(F(x)\).
Solution
If we look at a graph of the p.d.f. \(f(x)\):
we see that the cumulative distribution function \(F(x)\) must be defined over four intervals — for \(x\le -1\), when \(-1<x\le 0\), for \(0<x<1\), and for \(x\ge 1\). The definition of \(F(x)\) for \(x\le -1\) is easy. Since no probability accumulates over that interval, \(F(x)=0\) for \(x\le -1\). Similarly, the definition of \(F(x)\) for \(x\ge 1\) is easy. Since all of the probability has been accumulated for \(x\) beyond 1, \(F(x)=1\) for \(x\ge 1\). Now for the other two intervals:
In summary, the cumulative distribution function defined over the four intervals is:
\(\begin{equation}F(x)=\left\{\begin{array}{ll}
0, & \text { for } x \leq-1 \\
\frac{1}{2}(x+1)^{2}, & \text { for }-1<x \leq 0 \\
1-\frac{(1-x)^{2}}{2}, & \text { for } 0<x<1 \\
1, & \text { for } x \geqslant 1
\end{array}\right.\end{equation}\)
The cumulative distribution function is therefore a concave up parabola over the interval \(-1<x\le 0\) and a concave down parabola over the interval \(0<x<1\). Therefore, the graph of the cumulative distribution function looks something like this:
14.3 - Finding Percentiles
14.3 - Finding PercentilesAt some point in your life, you have most likely been told that you fall in the something-something percentile with regards to some measure. For example, if you are tall, you might have been told that you are in the 95th percentile in height, meaning that you are taller than 95% of the population. When you took the SAT Exams, you might have been told that you are in the 80th percentile in math ability, meaning that you scored better than 80% of the population on the math portion of the SAT Exams. We'll now formally define what a percentile is within the framework of probability theory.
Definition. If \(X\) is a continuous random variable, then the \((100p)^{th}\) percentile is a number \(\pi_p\) such that the area under \(f(x)\) and to the left of \(\pi_p\) is \(p\).
That is, \(p\) is the integral of \(f(x)\) from \(-\infty\) to \(\pi_p\):
\(p=\int_{-\infty}^{\pi_p} f(x)dx=F(\pi_p)\)
Some percentiles are given special names:
- The 25th percentile, \(\pi_{0.25}\), is called the first quartile (denoted \(q_1\)).
- The 50th percentile, \(\pi_{0.50}\), is called the median (denoted \(m\)) or the second quartile (denoted \(q_2\)).
- The 75th percentile, \(\pi_{0.75}\), is called the third quartile (denoted \(q_3\)).
Example 14-5
A prospective college student is told that if her total score on the SAT Exam is in the 99th percentile, then she can most likely attend the college of her choice. It is well-known that the distribution of SAT Exam scores is bell-shaped, and the average total score is typically around 1500. Here is a picture depicting the situation:
The student would like to know what her total score, \(\pi_{0.99}\), needs to be in order to ensure that she falls in the 99th percentile. Data from the 2009 SAT Exam Scores suggests that the student should obtain at least a 2200 on her exam. That is, \(\pi_{0.99}=2200\).
Example 14-6
Let \(X\) be a continuous random variable with the following probability density function:
\(f(x)=\dfrac{1}{2}\)
for \(0<x<2\). What is the first quartile, median, and third quartile of \(X\)?
Solution
Because the p.d.f. is uniform, meaning it remains constant over the support, we can readily find the percentiles in one of two ways. We can use the p.d.f. directly to find the first quartile, median, and third quartile:
Alternatively, we can use the cumulative distribution function:
Example 14-7
Let \(X\) be a continuous random variable with the following probability density function:
\(f(x)=\dfrac{1}{2}(x+1)\)
for \(-1<x<1\). What is the 64th percentile of \(X\)?
Solution
To find the 64th percentile, we first need to find the cumulative distribution function \(F(x)\). It is:
\(F(x)=\dfrac{1}{2}\int_{-1}^x(t+1)dt=\dfrac{1}{2} \left[\dfrac{(t+1)^2}{2}\right]^{t=x}_{t=-1}=\dfrac{1}{4}(x+1)^2\)
for \(-1<x<1\). Now, to find the 64th percentile, we just need to set 0.64 equal to \(F(\pi_{0.64})\) and solve for \(\pi_{0.64}\). That is, we need to solve for \(\pi_{0.64}\) in the following equation:
\(0.64=F(\pi_{0.64})=\dfrac{1}{4}(\pi_{0.64}+1)^2\)
Multiplying both sides by 4, we get:
\(2.56=(\pi_{0.64}+1)^2\)
Taking the square root of both sides, we get:
\(\pi_{0.64}+1=\pm \sqrt{2.56}=\pm 1.6\)
And, subtracting both sides by 1, we get:
\(\pi_{0.64}=-2.6 \text{ or } 0.60\)
Because the support is \(-1<x<1\), the 64th percentile and must be 0.6, not −2.6.
14.4 - Special Expectations
14.4 - Special ExpectationsThe special expectations, such as the mean, variance, and moment generating function, for continuous random variables are just a straightforward extension of those of the discrete case. Again, all we need to do is replace the summations with integrals.
- Expected Value
-
The expected value or mean of a continuous random variable \(X\) is:
\(\mu=E(X)=\int^{+\infty}_{-\infty} xf(x)dx\)
- Variance
-
The variance of a continuous random variable \(X\) is:
\(\sigma^2=Var(X)=E[(X-\mu)^2]=\int^{+\infty}_{-\infty}(x-\mu)^2 f(x)dx\)
Alternatively, you can still use the shortcut formula for the variance, \(\sigma^2=E(X^2)-\mu^2\), with:
\(E(X^2)=\int^{+\infty}_{-\infty} x^2 f(x)dx\)
- Standard Deviation
-
The standard deviation of a continuous random variable \(X\) is:
\(\sigma=\sqrt{Var(X)}\)
- Moment Generating Function
-
The moment generating function of a continuous random variable \(X\), if it exists, is:
\(M(t)=\int^{+\infty}_{-\infty} e^{tx}f(x)dx\)
for \(-h<t<h\).
As before, differentiating the moment generating function provides us with a way of finding the mean:
\(E(X)=M'(0)\)
and the variance:
\(\text{Var}(X)=M^{\prime\prime}(0)-\left(M^\prime(0)\right)^2\)
Example 14-2 Revisited Again
Suppose \(X\) is a continuous random variable with the following probability density function:
\(f(x)=3x^2, \qquad 0<x<1\)
What is the mean of \(X\)?
Solution
What is the variance of \(X\)?
Solution
Example 14-8
Suppose \(X\) is a continuous random variable with the following probability density function:
\(f(x)=xe^{-x}\)
for \(0<x<\infty\). Use the moment generating function \(M(t)\) to find the mean of \(X\).
Solution
The moment generating function is found by integrating:
\(M(t)=E(e^{tX})=\int^{+\infty}_0 e^{tx} (xe^{-x})dx=\int^{+\infty}_0 xe^{-x(1-t)}dx\)
Because the upper limit is \(\infty\), we can rewrite the integral using a limit:
\(M(t)=\lim\limits_{b \to \infty} \int_0^b xe^{-x(1-t)}dx\)
Now, you might recall from your study of calculus that integrating this beast is going to require integration by parts. If you need to integrate
\(\int udv\)
integration by parts tells us that the integral is:
\(\int udv=uv-\int vdu\)
In our case, let's let:
\(u=x\) and \(dv=e^{-x(1-t)}\)
Differentiating \(u\) and integrating \(dv\), we get:
\(du=dx\) and \(v=-\dfrac{1}{1-t}e^{-x(1-t)}\)
Therefore, using the integration by parts formula, we get:
\(M(t)=\lim\limits_{b \to \infty} \left\{\left[-\dfrac{1}{1-t}xe^{-x(1-t)}\right]_{x=0}^{x=b}-\left(-\dfrac{1}{1-t}\right)\int_0^be^{-x(1-t)}dx\right\}\)
Evaluating the first term at \(x=0\) and \(x=b\), and integrating the last term, we get:
\(M(t)=\lim\limits_{b \to \infty}\left\{\left[-\dfrac{1}{1-t} be^{-b(1-t)}\right]+\left(\dfrac{1}{1-t}\right) \left[\left(-\dfrac{1}{1-t}\right)e^{-x(1-t)}\right]_{x=0}^{x=b} \right\}\)
which, upon evaluating the last term at \(x=0\) and \(x=b\), as well as simplifying and distributing the limit as \(b\) goes to infinity, we get:
\(M(t)=\lim\limits_{b \to \infty}\left[-\dfrac{1}{1-t} \dfrac{b}{e^{b(1-t)}}\right]-\left(\dfrac{1}{1-t}\right)^2 \lim\limits_{b \to \infty}(e^{-b(1-t)}-1)\)
Now, taking the limit of the second term is straightforward:
\(\lim\limits_{b \to \infty}(e^{-b(1-t)}-1)=-1\)
Therefore:
\(M(t)=\lim\limits_{b \to \infty}\left[-\dfrac{1}{1-t} \dfrac{b}{e^{b(1-t)}}\right]+\left(\dfrac{1}{1-t}\right)^2\)
Now, if you take the limit of the first term as \(b\) goes to infinity, you can see that we get infinity over infinity! You might recall that in this situation we need to use what is called L'Hôpital's Rule. It tells us that we can find the limit of that first term by first differentiating the numerator and denominator separately. Doing just that, we get:
\(M(t)=\lim\limits_{b \to \infty}\left[-\dfrac{1}{1-t} \times \dfrac{1}{(1-t)e^{b(1-t)}}\right]+\left(\dfrac{1}{1-t}\right)^2\)
Now, if you take the limit as \(b\) goes to infinity, you see that the first term approaches 0. Therefore (finally):
\(M(t)=\left(\dfrac{1}{1-t}\right)^2\)
as long as \(t<1\). Now, with the hard work behind us, using the m.g.f. to find the mean of \(X\) is a straightforward exercise:
14.5 - Piece-wise Distributions and other Examples
14.5 - Piece-wise Distributions and other ExamplesSome distributions are split into parts. They are not necessarily continuous, but they are continuous over particular intervals. These types of distributions are known as Piecewise distributions. Below is an example of this type of distribution
\(\begin{align*} f(x)=\begin{cases} 2-4x, & x< 1/2\\ 4x-2, & x\ge 1/2 \end{cases} \end{align*}\)
for \(0<x<1\). The pdf of \(X\) is shown below.
The first step is to show this is a valid pdf. To show it is a valid pdf, we have to show the following:
-
\(f(x)>0\). We can see that \(f(x)\) is greater than or equal to 0 for all values of \(X\).
-
\(\int_S f(x)dx=1\).
\(\begin{align*} & \int_0^{1/2}2-4xdx+\int_{1/2}^1 4x-2dx\\ & = 2\left(\frac{1}{2}\right)-2\left(\frac{1}{4}\right)+2-2-\left[2\left(\frac{1}{4}\right)-1\right]\\ & = 1-\left(\frac{1}{2}\right)+2-2-\left(\frac{1}{2}\right)+1=2-1=1 \end{align*}\)
-
If \((a, b)\subset S\), then \(P(a<X<b)=\int_a^bf(x)dx\). Lets find the probability that \(X\) is between 0 and \(2/3\).
\(P(X<2/3)=\int_0^{1/2} 2-4xdx+\int_{1/2}^{2/3} 4x-2dx=\frac{5}{9}\)
The next step is to know how to find expectations of piecewise distributions. If we know how to do this, we can find the mean, variance, etc of a random variable with this type of distribution. Suppose we want to find the expected value, \(E(X)\).
\(\begin{align*}& E(X)=\int_0^{1/2} x(2-4x)dx+\int_{1/2}^1 x(4x-2)dx\\& =\left(x^2-\frac{4}{3}x^3\right)|_0^{1/2}+\left(\frac{4}{3}x^3-x^2\right)|_{1/2}^1=\frac{1}{2}\end{align*}\)
The variance and other expectations can be found similarly.
The final step is to find the cumulative distribution function. cdf. Recall the cdf of \(X\) is \(F_X(t)=P(X\le t)\). Therefore, for \(t<\frac{1}{2}\), we have
\(F_X(t)=\int_0^t 2-4xdx=2x-x^2|_0^t=2t-2t^2\)
and for \(t\ge\frac{1}{2}\) we have
\(\begin{align*} & F_X(t)=\int_0^{1/2}2-4xdx+\int_{1/2}^t 4x-2dx=\frac{1}{2}+\left(2x^2-2x\right)|_{1/2}^t\\ & =2t^2-2t+1 \end{align*}\)
Thus, the cdf of \(X\) is
\(\begin{equation*} F_X(t)=\begin{cases} 2t-2t^2 & 0<t<1/2\\ 2t^2-2t+1 & 1/2\le t<1 \end{cases} \end{equation*}\)
Example 14-9: Mixture Distribution
Let \(f_1(y)\) and \(f_2(y)\) be density functions, \(y\) is a real number, and let \(a\) be a constant such that \(0\le a\le 1\). Consider the function
\(f(y)=af_1(y)+(1-a)f_2(y)\)
-
First, lets show that \(f(y)\) is a density function. A density function of this form is referred to as a mixture density (a mixture of two different density functions). My research is based on mixture densities.
\(\begin{align*} & \int_{-\infty}^{\infty} af_1(y)+(1-a)f_2(y)dy=a\int f_1(y)dy+(1-a)\int f_2(y)dy\\ & = a(1)+(1-a)(1)=a+1-a=1 \end{align*}\)
-
Suppose that \(Y_1\) is a random variable with density function \(f_1(y)\) and that \(E(Y_1)=\mu_1\) and \(Var(Y_1)=\sigma^2_1\); and similarly suppose that \(Y_2\) is a random variable with density function \(f_2(y)\) and that \(E(Y_2)=\mu_2\) and \(Var(Y_2)=\sigma^2_2\). Assume that \(Y\) is a random variable whose density is a mixture of densities corresponding to \(Y_1\) and \(Y_2\).
-
We can find the expected value of \(Y\) in terms of \(a, \;\mu_1, \text{ and } \mu_2\).
\(\begin{align*} & E(Y)=\int yf(y)dy=\int y(af_1(y)+(1-a)f_2(y))dy\\ & = a\int yf_1(y)dy + (1-a) \int yf_2(y)dy=\\ & =a\mu_1+(1-a)\mu_2 \end{align*}\)
-
We can also find the variance of \(Y\) similar to the above.
\(\begin{align*} & E(Y^2)=\int ay^2f_1(y)+(1-a)y^2f_2(y)dy=aE(Y_1^2)+(1-a)E(Y_2^2)\\ & =a(\mu_1^2+\sigma^2_1)+(1-a)(\mu_2^2+\sigma_2^2)\\ & Var(Y)=E(Y^2)-E(Y)^2 \end{align*}\)
-
Additional Practice Problems
-
A random variable \(X\) has the following probability density function:
\(\begin{align*} f(x)=\begin{cases} \frac{1}{8}x & 0\le x\le 2\\ \frac{1}{4} & 4\le x\le 7 \end{cases}. \end{align*}\)
-
Find the cumulative distribution function (CDF) of \(X\).
We should do this in pieces:
\(F(x)=\int_0^x\frac{1}{8}xdx=\frac{x^2}{16}, \qquad 0\le x\le 2\)
Between 2 and 4, the cdf remains the same. Therefore,
\(F(x)=\frac{2^2}{16}=\frac{1}{4}, \qquad 2\le x<4\)
After 4, the cdf becomes:
\(F(x)=\frac{1}{4}+\int_4^x\frac{1}{4}dx=\frac{1}{4}+\frac{1}{4}x-1=\frac{x-3}{4}, \qquad 4\le x\le 7\)
Therefore, we have:
\(F(x)=\begin{cases}0, & x<0\\ \frac{x^2}{16}, & 0\le x<2\\ \frac{1}{4}, & 2\le x<4\\ \frac{x-3}{4}, & 4\le x\le 7\\ 1, & x>7 \end{cases}\)
-
Find the median of \(X\). It helps to plot the CDF.
The median is between 4 and 7 and \(P(X<4)=\frac{1}{4}\). Let \(m\) denote the median.
\(0.5=F(m)=\frac{m-3}{4}\qquad \Rightarrow m-3=2 \qquad \Rightarrow m=5\).
-
-
Let \(X\) have probability density function \(f_X\) and cdf \(F_X(x)\). Find the probability density function of the random variable \(Y\) in term of \(f_X\), if \(Y\) is defined by \(Y=aX+b\). HINT: Start with the definition of the cdf of \(Y\).
\(F_Y(y)=P(Y\le y)=P(aX+b\le y)=P\left(X\le \frac{y-b}{a}\right)=F_X\left(\frac{y-b}{a}\right)\)
We know \(\frac{\partial }{\partial y}F_Y(y)=f_Y(y)\). Therefore,
\(f_Y(y)=\frac{\partial }{\partial y}F_Y(y)=\frac{\partial }{\partial y}F_X\left(\frac{y-b}{a}\right)=f_X\left(\frac{y-b}{a}\right)\left(\frac{1}{a}\right)\)
14.6 - Uniform Distributions
14.6 - Uniform Distributions- Uniform Distribution
-
A continuous random variable \(X\) has a uniform distribution, denoted \(U(a,b)\), if its probability density function is:
\(f(x)=\dfrac{1}{b-a}\)
for two constants \(a\) and \(b\), such that \(a<x<b\). A graph of the p.d.f. looks like this:
Note that the length of the base of the rectangle is \((b-a)\), while the length of the height of the rectangle is \(\dfrac{1}{b-a}\). Therefore, as should be expected, the area under \(f(x)\) and between the endpoints \(a\) and \(b\) is 1. Additionally, \(f(x)>0\) over the support \(a<x<b\). Therefore, \(f(x)\) is a valid probability density function.
Because there are an infinite number of possible constants \(a\) and \(b\), there are an infinite number of possible uniform distributions. That's why this page is called Uniform Distributions (with an s!) and not Uniform Distribution (with no s!). That said, the continuous uniform distribution most commonly used is the one in which \(a=0\) and \(b=1\).
- Cumulative distribution Function of a Uniform Random Variable \(X\)
-
The cumulative distribution function of a uniform random variable \(X\) is:
\(F(x)=\dfrac{x-a}{b-a}\)
for two constants \(a\) and \(b\) such that \(a<x<b\). A graph of the c.d.f. looks like this:
As the picture illustrates, \(F(x)=0\) when \(x\) is less than the lower endpoint of the support (\(a\), in this case) and \(F(x)=1\) when \(x\) is greater than the upper endpoint of the support (\(b\), in this case). The slope of the line between \(a\) and \(b\) is, of course, \(\dfrac{1}{b-a}\).
14.7 - Uniform Properties
14.7 - Uniform PropertiesHere, we present and prove three key properties of a uniform random variable.
Theorem
The mean of a continuous uniform random variable defined over the support \(a<x<b\) is:
\(\mu=E(X)=\dfrac{a+b}{2}\)
Proof
Theorem
The variance of a continuous uniform random variable defined over the support \(a<x<b\) is:
\(\sigma^2=Var(X)=\dfrac{(b-a)^2}{12}\)
Proof
Because we just found the mean \(\mu=E(X)\) of a continuous random variable, it will probably be easiest to use the shortcut formula:
\(\sigma^2=E(X^2)-\mu^2\)
to find the variance. Let's start by finding \(E(X^2)\):
Now, using the shortcut formula and what we now know about \(E(X^2)\) and \(E(X)\), we have:
\(\sigma^2=E(X^2)-\mu^2=\dfrac{b^2+ab+a^2}{3}-\left(\dfrac{b+a}{2}\right)^2\)
Simplifying a bit:
\(\sigma^2=\dfrac{b^2+ab+a^2}{3}-\dfrac{b^2+2ab+a^2}{4}\)
and getting a common denominator:
\(\sigma^2=\dfrac{4b^2+4ab+4a^2-3b^2-6ab-3a^2}{12}\)
Simplifying a bit more:
\(\sigma^2=\dfrac{b^2-2ab+a^2}{12}\)
and, finally, we have:
\(\sigma^2=\dfrac{(b-a)^2}{12}\)
as was to be proved.
Theorem
The moment generating function of a continuous uniform random variable defined over the support \(a < x < b\) is:
\(M(t)=\dfrac{e^{tb}-e^{ta}}{t(b-a)}\)
Proof
14.8 - Uniform Applications
14.8 - Uniform ApplicationsPerhaps not surprisingly, the uniform distribution is not particularly useful in describing much of the randomness we see in the natural world. Its claim to fame is instead its usefulness in random number generation. That is, approximate values of the \(U(0,1)\) distribution can be simulated on most computers using a random number generator. The generated numbers can then be used to randomly assign people to treatments in experimental studies, or to randomly select individuals for participation in a survey.
Before we explore the above-mentioned applications of the \(U(0,1)\) distribution, it should be noted that the random numbers generated from a computer are not technically truly random, because they are generated from some starting value (called the seed). If the same seed is used again and again, the same sequence of random numbers will be generated. It is for this reason that such random number generation is sometimes referred to as pseudo-random number generation. Yet, despite a sequence of random numbers being pre-determined by a seed number, the numbers do behave as if they are truly randomly generated, and are therefore very useful in the above-mentioned applications. They would probably not be particularly useful in the applications of cryptography or internet security, however!
Quantile-Quantile (Q-Q) Plots
Before we jump in and use a computer and a \(U(0,1)\) distribution to make random assignments and random selections, it would be useful to discuss how we might evaluate if a particular set of data follow a particular probability distribution. One possibility is to compare the theoretical mean (\(\mu\)) and variance (\(\sigma^2\)) with the sample mean ( \(\bar{x}\)) and sample variance (\(s^2\)). It shouldn't be surprising that such a comparison is hardly sufficient. Another technique used frequently is the creation of what is called a quantile-quantile plot (or a q-q plot, for short. The basic idea behind a q-q plot is a two-step process: 1) first determine the theoretical quantiles (from the supposed probability distribution) and the sample quantiles (from the data), and then 2) compare them on a plot. If the theoretical and sample quantiles "match," there is good evidence that the data follow the supposed probability distribution. Here are the specific details of how to create a q-q plot:
-
Determine the theoretical quantile of order \(p\), that is, the \((100p)^{th}\) percentile \(\pi_p\).
-
Determine the sample quantile, \(y_r\), of order \(\dfrac{r}{n+1}\), that is the \(100\dfrac{r}{n+1}\) percentile. While that might sound complicated, it amounts to just ordering the data \(x_1, x_2, \ldots, x_n\) to get the order statistics \(y_1\le y_2\le \ldots \le y_n\).
-
Plot the theoretical quantile on the y-axis against the sample quantile on the x-axis. If the sample data follow the theoretical probability distribution, we would expect the points \((y_r, \pi_p)\) to lie close to a line through the origin with slope equal to one.
In the case of the \(U(0,1)\) distribution, the cumulative distribution function is \(F(x)=x\). Now, recall that to find the \((100p)^{th}\) percentile \(\pi_p\), we set \(p\) equal to \(F(\pi_p)\) and solve for \(\pi_p\). That means in the case of the \(U(0,1)\) distribution, we set \(F(\pi_p)=\pi_p\) equal to \(p\) and solve for \(\pi_p\). Ahhhhaaa! In the case of the \(U(0,1)\) distribution, \(\pi_p=p\). That is, \(\pi_{0.05}=0.05\), \(\pi_{0.35}=0.35\), and so on. Let's take a look at an example!
Example 14-9
Consider the following set of 19 numbers generated from Minitab's \(U(0,1)\) random number generator. Do these data appear to have come from the probability model given by \(f(x)=1\) for \(0<x<1\)?
| Uniform | |||||
|---|---|---|---|---|---|
| 0.790222 | 0.367893 | 0.446442 | 0.889043 | 0.227839 | 0.541575 |
| 0.805958 | 0.156496 | 0.157753 | 0.465619 | 0.805580 | 0.784926 |
| 0.288771 | 0.010717 | 0.511768 | 0.496895 | 0.076856 | 0.254670 |
| 0.752679 |
Solution
Here are the original data (the column labeled Uniform) along with their sample quantiles (the column labeled Sorted) and their theoretical quantiles (the column labeled Percent):
| r | Uniform | Sorted | Percent |
|---|---|---|---|
| 1 | 0.790222 | 0.010717 | 0.05 |
| 2 | 0.367893 | 0.076856 | 0.10 |
| 3 | 0.446442 | 0.156496 | 0.15 |
| 4 | 0.889043 | 0.157753 | 0.20 |
| 5 | 0.227839 | 0.227839 | 0.25 |
| 6 | 0.541575 | 0.254670 | 0.30 |
| 7 | 0.805958 | 0.288771 | 0.35 |
| 8 | 0.156496 | 0.367893 | 0.40 |
| 9 | 0.157753 | 0.446442 | 0.45 |
| 10 | 0.465619 | 0.465619 | 0.50 |
| 11 | 0.805580 | 0.496895 | 0.55 |
| 12 | 0.784926 | 0.511768 | 0.60 |
| 13 | 0.288771 | 0.541575 | 0.65 |
| 14 | 0.010717 | 0.752679 | 0.70 |
| 15 | 0.511768 | 0.784926 | 0.75 |
| 16 | 0.496895 | 0.790222 | 0.80 |
| 17 | 0.076856 | 0.805580 | 0.85 |
| 18 | 0.254670 | 0.805958 | 0.90 |
| 19 | 0.7526679 | 0.889043 | 0.95 |
As might be obvious, the Sorted column is just the original data in increasing sorted order. The Percent column is determined from the \(\pi_p=p\) relationship. In a set of 19 data points, we'd expect the 1st of the 19 points to be the 1/20th or fifth percentile, we'd expect the 2nd of the 19 points to be the 2/20th or tenth percentile, and so on. Plotting the Percent column on the vertical axis (labeled Theoretical Quantile) and the Sorted column on the horizontal axis (labeled Sample Quantile), here's the resulting q-q plot:
Now, the key to interpreting q-q plots is to do it loosely! If the data points generally follow an (approximate) straight line, then go ahead and conclude that the data follow the tested probability distribution. That's what we'll do here!
Incidentally, the theoretical mean and variance of the \(U(0,1)\) distribution are \(\dfrac{1}{2}=0.5\) and \(\dfrac{1}{12}=0.0833\), respectively. If you calculate the sample mean and sample variance of the 19 data points, you'll find that they are 0.4648 and 0.078, respectively. Not too shabby of an approximation for such a small data set.
Random Assignment to Treatment
As suggested earlier, the \(U(0,1)\) distribution can be quite useful in randomly assigning experimental units to the treatments in an experiment. First, let's review why randomization is a useful venture when conducting an experiment. Suppose we were interested in measuring how high a person could reach after "taking" an experimental treatment. It would be awfully hard to draw a strong conclusion about the effectiveness of the experimental treatment if the people in one treatment group were, to begin with, significantly taller than the people in the other treatment group. Randomly assigning people to the treatments in an experiment minimize the chances that such important differences exist in the treatment groups. That way if differences exist in the two groups at the conclusion of the study with respect to the primary variable of interest, we can feel confident in attributing the difference strongly to the treatment of interest rather than due to some other fundamental difference in the groups.
Okay, now let's talk about how the \(U(0,1)\) distribution can help us randomly assign the experimental units to the treatments in a completely randomized experiment. For the sake of concreteness, suppose we wanted to randomly assign 20 students to one group (those who complete a blue data collection form, say) and 20 students to a second group (those who complete a green data collection form, say). This is what the procedure might look like:
-
Assign the pool of 40 potential students each one number from 1 to 40. It doesn't matter how you assign these numbers.
-
Generate 40 \(U(0,1)\) numbers in one column of a spreadsheet. Enter the numbers 1 to 40 in a second column of a spreadsheet.
-
Sort the 40 \(U(0,1)\) numbers in sorted increasing order, so that the numbers in the second column follow along during the sorting process. For example, if the 13th generated \(U(0,1)\) number was the smallest number generated, then the number 13 should appear, after sorting, in the first row of the second column. If the 24th generated \(U(0,1)\) number was the second smallest number generated, the number 24 should appear, after sorting, in the second row of the second column. And so on.
-
The students whose numbers appear in the first 20 rows of the second column should be assigned to complete the blue data collection form. The students whose numbers appear in the second 20 rows of the second column should be assigned to complete the green data collection form.
One semester, I conducted the above experiment exactly as described. Twenty students were randomly assigned to complete a blue version of the following form, and the remaining twenty students were randomly assigned to complete a green version of the form:
| Data Collection Form | ||
|---|---|---|
| 1. What is your gender? | Male ___ | Female ___ |
| 2. What is your current cumulative grade point average? | ___.___ ___ | |
| 3. What is your height? | ___ ___.___ inches | (or ___ ___ ___.___ centimeters) |
| 4. What is your weight? | ___ ___ ___.___ pounds | (or ___ ___ ___.___ kilograms) |
| 5. Excluding class time, how much do you study for this course? | ___ ___ hours/week | |
| 6. What is your current exam average in this class? | ___ ___ ___ | |
| 7. Are you a native resident of Pennsylvania? | Yes ___ | No ___ |
| 8. How many credits are you taking this semester? | ___ ___ credits |
After administering the forms to the 40 students, here's what the resulting data looked like:
| ROW | COLOR | GENDER | GPA | HEIGHT | WEIGHT | HOURS | EXAM | NATIVE | CREDITS |
| 1 | blue | 1 | 3.44 | 68.00 | 140.0 | 2.0 | 85.0 | 1 | 18.0 |
| 2 | blue | 1 | 3.90 | 71.00 | 210.0 | 1.0 | 98.5 | 0 | 18.0 |
| 3 | blue | 2 | * | 68.00 | 200.0 | 10.0 | 83.0 | 0 | 9.0 |
| 4 | blue | 2 | * | 67.00 | 185.0 | 4.0 | 100.0 | 1 | 10.0 |
| 5 | blue | 1 | 3.82 | 66.00 | 143.0 | 3.0 | 98.0 | 0 | 9.0 |
| 6 | blue | 2 | 3.66 | 66.00 | 140.0 | 5.0 | 91.5 | 0 | 17.0 |
| 7 | blue | 2 | 2.98 | 66.00 | 135.0 | 4.0 | 71.0 | 1 | 16.0 |
| 8 | blue | 2 | 3.67 | 67.00 | 118.0 | 5.0 | 65.0 | 1 | 18.0 |
| 9 | blue | 1 | 3.15 | 69.50 | 180.5 | 10.0 | 61.0 | 1 | 13.0 |
| 10 | blue | 1 | 3.29 | 72.00 | 120.0 | 2.0 | 61.0 | 1 | 17.0 |
| 11 | blue | 1 | 4.00 | 69.00 | 175.0 | 4.0 | 95.0 | 0 | 3.0 |
| 12 | blue | 2 | 2.46 | 69.70 | 181.0 | 7.0 | 59.0 | 0 | 16.0 |
| 13 | blue | 2 | 2.97 | 52.00 | 105.0 | 6.0 | 62.0 | 0 | 15.0 |
| 14 | blue | 1 | * | 68.80 | 136.5 | 2.0 | 95.0 | 0 | 12.0 |
| 15 | blue | 1 | 3.50 | 70.00 | 215.0 | 1.0 | 87.5 | 1 | 15.0 |
| 16 | blue | 2 | 3.61 | 65.00 | 135.0 | 9.0 | 89.0 | 0 | 12.0 |
| 17 | blue | 2 | 3.24 | 64.00 | 148.0 | 10.0 | 65.0 | 1 | 16.0 |
| 18 | blue | 2 | 3.41 | 65.50 | 126.0 | 5.0 | 70.0 | 1 | 15.0 |
| 19 | blue | 2 | 3.40 | 65.00 | 115.0 | 2.0 | 83.0 | 1 | 17.0 |
| 20 | blue | 1 | 3.80 | 68.00 | 236.0 | 6.0 | 87.5 | 1 | 18.0 |
| 21 | blue | 2 | 2.95 | 65.00 | 140.0 | 6.0 | 79.0 | 1 | 15.0 |
| 22 | green | 1 | 3.80 | 71.50 | 145.0 | 3.0 | 77.5 | 1 | 18.0 |
| 23 | green | 2 | 4.00 | 62.00 | 185.0 | 6.0 | 98.0 | 1 | 10.0 |
| 24 | green | 2 | * | 60.00 | 100.0 | 8.0 | 95.0 | 0 | 10.0 |
| 25 | green | 2 | 3.65 | 62.00 | 150.0 | 4.0 | 85.0 | 1 | 15.0 |
| 26 | green | 1 | 3.54 | 71.75 | 160.0 | 0.5 | 83.0 | 1 | 6.0 |
| 27 | green | 2 | * | 65.00 | 113.0 | 7.0 | 97.5 | 0 | 18.0 |
| 28 | green | 1 | 3.63 | 69.50 | 155.0 | 10.0 | 80.0 | 1 | 18.0 |
| 29 | green | 2 | 3.90 | 65.20 | 110.0 | 1.0 | 96.0 | 0 | 9.0 |
| 30 | green | 1 | * | 76.00 | 165.0 | 3.0 | 88.0 | 1 | 15.0 |
| 31 | green | 1 | 3.80 | 70.40 | 143.0 | 1.0 | 100.0 | 0 | 9.0 |
| 32 | green | 2 | 3.19 | 64.50 | 140.0 | 10.0 | 65.0 | 1 | 16.0 |
| 33 | green | 1 | 2.97 | 71.00 | 140.0 | 5.0 | 72.0 | 1 | 17.5 |
| 34 | green | 1 | 2.87 | 65.50 | 160.3 | 7.0 | 45.0 | 1 | 13.0 |
| 35 | green | 1 | 3.43 | 60.70 | 160.0 | 12.0 | 90.0 | 0 | 12.0 |
| 36 | green | 1 | 3.61 | 66.00 | 126.0 | 18.0 | 88.0 | 0 | 13.0 |
| 37 | green | 1 | * | 66.00 | 120.0 | 7.0 | 79.0 | 1 | 15.0 |
| 38 | green | 1 | 2.97 | 69.70 | 185.5 | 6.0 | 83.0 | 1 | 13.0 |
| 39 | green | 1 | 3.26 | 70.00 | 152.0 | 3.0 | 70.5 | 1 | 13.0 |
| 40 | green | 1 | 3.30 | 72.00 | 190.0 | 2.5 | 81.0 | 1 | 17.0 |
And, here's a portion of a basic descriptive analysis of six of the variables on the form:
| VARIABLE | COLOR | N | N* | MEAN | MEDIAN | TrMean |
| GPA | blue | 18 | 3 | 3.4028 | 3.4250 | 3.4244 |
| green | 15 | 4 | 3.4613 | 3.5400 | 3.4654 | |
| HEIGHT | blue | 21 | 0 | 66.786 | 67.000 | 67.289 |
| green | 19 | 0 | 67.30 | 66.00 | 67.22 | |
| WEIGHT | blue | 21 | 0 | 156.38 | 140.00 | 154.89 |
| green | 19 | 0 | 147.36 | 150.00 | 147.64 | |
| HOURS | blue | 21 | 0 | 4.952 | 5.000 | 4.895 |
| green | 19 | 0 | 5.526 | 6.000 | 5.441 | |
| EXAM | blue | 21 | 0 | 80.29 | 83.00 | 80.37 |
| green | 19 | 0 | 82.82 | 83.00 | 84.03 | |
| CREDITS | blue | 21 | 0 | 14.238 | 15.000 | 14.632 |
| green | 19 | 0 | 13.553 | 13.000 | 13.735 |
| VARIABLE | COLOR | StDev | SE Mean | MINIMUM | MAXIMUM | Q1 |
| GPA | blue | 0.3978 | 0.0938 | 2.4600 | 4.0000 | 3.1075 |
| green | 0.3564 | 0.0920 | 2.8700 | 4.0000 | 3.1900 | |
| HEIGHT | blue | 4.025 | 0.878 | 52.000 | 72.000 | 65.250 |
| green | 4.43 | 1.02 | 60.00 | 76.00 | 64.50 | |
| WEIGHT | blue | 36.97 | 8.07 | 105.00 | 236.00 | 130.50 |
| green | 25.53 | 5.86 | 100.00 | 190.00 | 126.00 | |
| HOURS | blue | 2.941 | 0.642 | 1.000 | 10.000 | 2.000 |
| green | 3.251 | 0.746 | 0.500 | 12.000 | 3.000 | |
| EXAM | blue | 14.5 | 3.09 | 59.00 | 100.00 | 65.00 |
| green | 13.42 | 3.08 | 45.00 | 100.00 | 77.50 | |
| CREDITS | blue | 3.885 | 0.848 | 3.000 | 18.000 | 12.000 |
| green | 3.547 | 0.814 | 6.000 | 18.000 | 10.000 |
| VARIABLE | COLOR | Q3 |
| GPA | blue | 3.7025 |
| green | 3.8000 | |
| HEIGHT | blue | 69.250 |
| green | 71.00 | |
| WEIGHT | blue | 183.00 |
| green | 160.30 | |
| HOURS | blue | 6.500 |
| green | 8.000 | |
| EXAM | blue | 93.25 |
| green | 95.00 | |
| CREDITS | blue | 17.000 |
| green | 17.000 |
The analysis suggests that my randomization worked quite well. For example, the mean grade-point average of those students completing the blue form was 3.40, while the mean g.p.a. for those students completing the green form was 3.46. And, the mean height of those students completing the blue form was 66.8 inches, while the mean height for those students completing the green form was 67.3 inches. The two groups appear to be similar, on average, with respect to the other collected data as well. It should be noted that there is no guarantee that any particular randomization will be as successful as the one I illustrated here. The only thing that the randomization ensures is that the chance that the groups will differ with respect to key measurements will be small.
Random Selection for Participation in a Survey
Just as you should always randomly assign experimental units to treatments when conducting an experiment, you should always randomly select your participants when conducting a survey. If you don't, you might very well end up with biased survey results. (The people who choose to take the time to complete a survey in a magazine or on a web site typically have quite strong opinions!) The procedure we can use to randomly select participants for a survey is quite similar to that used for randomly assigning people to treatments in a completely randomized experiment. This is what the procedure would look like if you wanted to randomly select, say, 1000 students to participate in a survey from a potential pool of, say, 40000 students:
-
Assign the pool of 40000 potential participants each one number from 1 to 40000. It doesn't matter how you assign these numbers.
-
Generate 40000 \(U(0,1)\) numbers in one column of a spreadsheet. Enter the numbers 1 to 40000 in a second column of a spreadsheet.
-
Sort the 40000 \(U(0,1)\) numbers in sorted increasing order, so that the numbers in the second column follow along during the sorting process. For example, if the 23rd generated \(U(0,1)\) number was the smallest number generated, the number 23 should appear, after sorting, in the first row of the second column. If the 102nd generated \(U(0,1)\) number was the second smallest number generated, the number 102 should appear, after sorting, in the second row of the second column. And so on.
-
The students whose numbers appear in the first 1000 rows of the second column should be selected to participate in the survey.
Following the procedure as described, the 1000 selected students represent a random sample from the population of 40000 students.
Lesson 15: Exponential, Gamma and Chi-Square Distributions
Lesson 15: Exponential, Gamma and Chi-Square DistributionsOverview
In this Chapter, we investigate the probability distributions of continuous random variables that are so important to the field of statistics that they are given special names. They are:
- the uniform distribution (Lesson 14)
- the exponential distribution
- the gamma distribution
- the chi-square distribution
- the normal distribution
In this lesson, we will investigate the probability distribution of the waiting time, \(X\), until the first event of an approximate Poisson process occurs. We will learn that the probability distribution of \(X\) is the exponential distribution with mean \(\theta=\dfrac{1}{\lambda}\). In this lesson, we investigate the waiting time, \(W\), until the \(\alpha^{th}\) (that is, "alpha"-th) event occurs. As we'll soon learn, that distribution is known as the gamma distribution. After investigating the gamma distribution, we'll take a look at a special case of the gamma distribution, a distribution known as the chi-square distribution.
Objectives
- To learn a formal definition of the probability density function of a (continuous) exponential random variable.
- To learn key properties of an exponential random variable, such as the mean, variance, and moment generating function.
- To understand the steps involved in each of the proofs in the lesson.
- To be able to apply the methods learned in the lesson to new problems. To understand the motivation and derivation of the probability density function of a (continuous) gamma random variable.
- To understand the effect that the parameters \(\alpha\) and \(\theta\) have on the shape of the gamma probability density function.
- To learn a formal definition of the gamma function.
- To learn a formal definition of the probability density function of a gamma random variable.
- To learn key properties of a gamma random variable, such as the mean, variance, and moment generating function.
- To learn a formal definition of the probability density function of a chi-square random variable.
- To understand the relationship between a gamma random variable and a chi-square random variable.
- To learn key properties of a chi-square random variable, such as the mean, variance, and moment generating function.
- To learn how to read a chi-square value or a chi-square probability off of a typical chi-square cumulative probability table.
- To understand the steps involved in each of the proofs in the lesson.
- To be able to apply the methods learned in the lesson to new problems.
15.1 - Exponential Distributions
15.1 - Exponential DistributionsExample 15-1
Suppose \(X\), following an (approximate) Poisson process, equals the number of customers arriving at a bank in an interval of length 1. If \(\lambda\), the mean number of customers arriving in an interval of length 1, is 6, say, then we might observe something like this:
In this particular representation, seven (7) customers arrived in the unit interval. Previously, our focus would have been on the discrete random variable \(X\), the number of customers arriving. As the picture suggests, however, we could alternatively be interested in the continuous random variable \(W\), the waiting time until the first customer arrives. Let's push this a bit further to see if we can find \(F(w)\), the cumulative distribution function of \(W\):
Now, to find the probability density function \(f(w)\), all we need to do is differentiate \(F(w)\). Doing so, we get:
\(f(w)=F'(w)=-e^{-\lambda w}(-\lambda)=\lambda e^{-\lambda w}\)
for \(0<w<\infty\). Typically, though we "reparameterize" before defining the "official" probability density function. If \(\lambda\) (the Greek letter "lambda") equals the mean number of events in an interval, and \(\theta\) (the Greek letter "theta") equals the mean waiting time until the first customer arrives, then:
\(\theta=\dfrac{1}{\lambda}\) and \(\lambda=\dfrac{1}{\theta}\)
For example, suppose the mean number of customers to arrive at a bank in a 1-hour interval is 10. Then, the average (waiting) time until the first customer is \(\frac{1}{10}\) of an hour, or 6 minutes.
Let's now formally define the probability density function we have just derived.
- Exponential Distribution
-
The continuous random variable \(X\) follows an exponential distribution if its probability density function is:
\(f(x)=\dfrac{1}{\theta} e^{-x/\theta}\)
for \(\theta>0\) and \(x\ge 0\).
Because there are an infinite number of possible constants \(\theta\), there are an infinite number of possible exponential distributions. That's why this page is called Exponential Distributions (with an s!) and not Exponential Distribution (with no s!).
15.2 - Exponential Properties
15.2 - Exponential PropertiesHere, we present and prove four key properties of an exponential random variable.
Theorem
The exponential probability density function:
\(f(x)=\dfrac{1}{\theta} e^{-x/\theta}\)
for \(x\ge 0\) and \(\theta>0\) is a valid probability density function.
Proof
Theorem
The moment generating function of an exponential random variable \(X\) with parameter \(\theta\) is:
\(M(t)=\dfrac{1}{1-\theta t}\)
for \(t<\frac{1}{\theta}\).
Proof
\(M(t)=E(e^{tX})=\int_0^\infty e^{tx} \left(\dfrac{1}{\theta}\right) e^{-x/\theta} dx\)
Simplifying and rewriting the integral as a limit, we have:
\(M(t)=\dfrac{1}{\theta}\lim\limits_{b \to \infty} \int_0^b e^{x(t-1/\theta)} dx\)
Integrating, we have:
\(M(t)=\dfrac{1}{\theta}\lim\limits_{b \to \infty} \left[ \dfrac{1}{t-1/\theta} e^{x(t-1/\theta)} \right]^{x=b}_{x=0}\)
Evaluating at \(x=0\) and \(x=b\), we have:
\(M(t)=\dfrac{1}{\theta}\lim\limits_{b \to \infty} \left[ \dfrac{1}{t-1/\theta} e^{b(t-1/\theta)} - \dfrac{1}{t-1/\theta} \right]=\dfrac{1}{\theta}\lim\limits_{b \to \infty} \left\{ \left(\dfrac{1}{t-1/\theta}\right) e^{b(t-1/\theta)} \right\}-\dfrac{1}{t-1/\theta}\)
Now, the limit approaches 0 provided \(t-\frac{1}{\theta}<0\), that is, provided \(t<\frac{1}{\theta}\), and so we have:
\(M(t)=\dfrac{1}{\theta} \left(0-\dfrac{1}{t-1/\theta}\right)\)
Simplifying more:
\(M(t)=\dfrac{1}{\theta} \left(-\dfrac{1}{\dfrac{\theta t-1}{\theta}}\right)=\dfrac{1}{\theta}\left(-\dfrac{\theta}{\theta t-1}\right)=-\dfrac{1}{\theta t-1}\)
and finally:
\(M(t)=\dfrac{1}{1-\theta t}\)
provided \(t<\frac{1}{\theta}\), as was to be proved.
Theorem
The mean of an exponential random variable \(X\) with parameter \(\theta\) is:
\(\mu=E(X)=\theta\)
Proof
Theorem
The variance of an exponential random variable \(X\) with parameter \(\theta\) is:
\(\sigma^2=Var(X)=\theta^2\)
Proof
15.3 - Exponential Examples
15.3 - Exponential ExamplesExample 15-2
Students arrive at a local bar and restaurant according to an approximate Poisson process at a mean rate of 30 students per hour. What is the probability that the bouncer has to wait more than 3 minutes to card the next student?
Solution
If we let \(X\) equal the number of students, then the Poisson mean \(\lambda\) is 30 students per 60 minutes, or \(\dfrac{1}{2}\) student per minute! Now, if we let \(W\) denote the (waiting) time between students, we can expect that there would be, on average, \(\theta=\dfrac{1}{\lambda}=2\) minutes between arriving students. Because \(W\) is (assumed to be) exponentially distributed with mean \(\theta=2\), its probability density function is:
\(f(w)=\dfrac{1}{2} e^{-w/2}\)
for \(w\ge 0\). Now, we just need to find the area under the curve, and greater than 3, to find the desired probability:
Example 15-3
The number of miles that a particular car can run before its battery wears out is exponentially distributed with an average of 10,000 miles. The owner of the car needs to take a 5000-mile trip. What is the probability that he will be able to complete the trip without having to replace the car battery?
Solution
At first glance, it might seem that a vital piece of information is missing. It seems that we should need to know how many miles the battery in question already has on it before we can answer the question! Hmmm.... or do we? Well, let's let \(X\) denote the number of miles that the car can run before its battery wears out. Now, suppose the following is true:
\(P(X>x+y|X>x)=P(X>y)\)
If it is true, it would tell us that the probability that the car battery wears out in more than \(y=5000\) miles doesn't matter if the car battery was already running for \(x=0\) miles or \(x=1000\) miles or \(x=15000\) miles. Now, we are given that \(X\) is exponentially distributed. It turns out that the above statement is true for the exponential distribution (you will be asked to prove it for homework)! It is for this reason that we say that the exponential distribution is "memoryless."
It can also be shown (do you want to show that one too?) that if \(X\) is exponentially distributed with mean \(\theta\), then:
\(P(X>k)=e^{-k/\theta}\)
Therefore, the probability in question is simply:
\(P(X>5000)=e^{-5000/10000}=e^{-1/2}\approx 0.604\)
We'll leave it to the gentleman in question to decide whether that probability is large enough to give him comfort that he won't be stranded somewhere along a remote desert highway!
15.4 - Gamma Distributions
15.4 - Gamma DistributionsThe Situation
In the previous lesson, we learned that in an approximate Poisson process with mean \(\lambda\), the waiting time \(X\) until the first event occurs follows an exponential distribution with mean \(\theta=\frac{1}{\lambda}\). We now let \(W\) denote the waiting time until the \(\alpha^{th}\) event occurs and find the distribution of \(W\). We could represent the situation as follows:
Derivation of the Probability Density Function
Just as we did in our work with deriving the exponential distribution, our strategy here is going to be to first find the cumulative distribution function \(F(w)\) and then differentiate it to get the probability density function \(f(w)\). Now, for \(w>0\) and \(\lambda>0\), the definition of the cumulative distribution function gives us:
\(F(w)=P(W\le w)\)
The rule of complementary events tells us then that:
\(F(w)=1-P(W> w)\)
Now, the waiting time \(W\) is greater than some value \(w\) only if there are fewer than \(\alpha\) events in the interval \([0,w]\). That is:
\(F(w)=1-P(\text{fewer than }\alpha\text{ events in } [0,w]) \)
A more specific way of writing that is:
\(F(w)=1-P(\text{0 events or 1 event or ... or }(\alpha-1)\text{ events in } [0,w]) \)
Those mutually exclusive "ors" mean that we need to add up the probabilities of having 0 events occurring in the interval \([0,w]\), 1 event occurring in the interval \([0,w]\), ..., up to \((\alpha-1)\) events in \([0,w]\). Well, that just involves using the probability mass function of a Poisson random variable with mean \(\lambda w\). That is:
\(F(w)=1-\sum\limits_{k=0}^{\alpha-1} \dfrac{(\lambda w)^k e^{-\lambda w}}{k!}\)
Now, we could leave \(F(w)\) well enough alone and begin the process of differentiating it, but it turns out that the differentiation goes much smoother if we rewrite \(F(w)\) as follows:
\(F(w)=1-e^{-\lambda w}-\sum\limits_{k=1}^{\alpha-1} \dfrac{1}{k!} \left[(\lambda w)^k e^{-\lambda w}\right]\)
As you can see, we merely pulled the \(k=0\) out of the summation and rewrote the probability mass function so that it would be easier to administer the product rule for differentiation.
Now, let's do that differentiation! We need to differentiate \(F(w)\) with respect to \(w\) to get the probability density function \(f(w)\). Using the product rule, and what we know about the derivative of \(e^{\lambda w}\) and \((\lambda w)^k\), we get:
\(f(w)=F'(w)=\lambda e^{-\lambda w} -\sum\limits_{k=1}^{\alpha-1} \dfrac{1}{k!} \left[(\lambda w)^k \cdot (-\lambda e^{-\lambda w})+ e^{-\lambda w} \cdot k(\lambda w)^{k-1} \cdot \lambda \right]\)
Pulling \(\lambda e^{-\lambda w}\) out of the summation, and dividing \(k\) by \(k!\) (to get \( \frac{1}{(k-1)!}\)) in the second term in the summation, we get that \(f(w)\) equals:
\(=\lambda e^{-\lambda w}+\lambda e^{-\lambda w}\left[\sum\limits_{k=1}^{\alpha-1} \left\{ \dfrac{(\lambda w)^k}{k!}-\dfrac{(\lambda w)^{k-1}}{(k-1)!} \right\}\right]\)
Evaluating the terms in the summation at \(k=1, k=2\), up to \(k=\alpha-1\), we get that \(f(w)\) equals:
\(=\lambda e^{-\lambda w}+\lambda e^{-\lambda w}\left[(\lambda w-1)+\left(\dfrac{(\lambda w)^2}{2!}-\lambda w\right)+\cdots+\left(\dfrac{(\lambda w)^{\alpha-1}}{(\alpha-1)!}-\dfrac{(\lambda w)^{\alpha-2}}{(\alpha-2)!}\right)\right]\)
Do some (lots of!) crossing out (\(\lambda w -\lambda w =0\), for example), and a bit more simplifying to get that \(f(w)\) equals:
\(=\lambda e^{-\lambda w}+\lambda e^{-\lambda w}\left[-1+\dfrac{(\lambda w)^{\alpha-1}}{(\alpha-1)!}\right]=\lambda e^{-\lambda w}-\lambda e^{-\lambda w}+\dfrac{\lambda e^{-\lambda w} (\lambda w)^{\alpha-1}}{(\alpha-1)!}\)
And since \(\lambda e^{-\lambda w}=\lambda e^{-\lambda w}=0\), we get that \(f(w)\) equals:
\(=\dfrac{\lambda e^{-\lambda w} (\lambda w)^{\alpha-1}}{(\alpha-1)!}\)
Are we there yet? Almost! We just need to reparameterize (if \(\theta=\frac{1}{\lambda}\), then \(\lambda=\frac{1}{\theta}\)). Doing so, we get that the probability density function of \(W\), the waiting time until the \(\alpha^{th}\) event occurs, is:
\(f(w)=\dfrac{1}{(\alpha-1)! \theta^\alpha} e^{-w/\theta} w^{\alpha-1}\)
for \(w>0, \theta>0\), and \(\alpha>0\).
Effect of \(\theta\) and \(\alpha\) on the Distribution
Recall that \(\theta\) is the mean waiting time until the first event, and \(\alpha\) is the number of events for which you are waiting to occur. It makes sense then that for fixed \(\alpha\), as \(\theta\) increases, the probability "moves to the right," as illustrated here with \(\alpha\)fixed at 3, and \(\theta\) increasing from 1 to 2 to 3:
The plots illustrate, for example, that if we are waiting for \(\alpha=3\) events to occur, we have a greater probability of our waiting time \(X\) being large if our mean waiting time until the first event is large (\(\theta=3\), say) than if it is small (\(\theta=1\), say).
It also makes sense that for fixed \(\theta\), as \(\alpha\) increases, the probability "moves to the right," as illustrated here with \(\theta\)fixed at 3, and \(\alpha\) increasing from 1 to 2 to 3:
The plots illustrate, for example, that if the mean waiting time until the first event is \(\theta=3\), then we have a greater probability of our waiting time \(X\) being large if we are waiting for more events to occur (\(\alpha=3\), say) than fewer (\(\alpha=1\), say).
15.5 - The Gamma Function
15.5 - The Gamma FunctionAn Aside
- The gamma function, denoted \(\Gamma(t)\), is defined, for \(t>0\), by:
\(\Gamma(t)=\int_0^\infty y^{t-1} e^{-y} dy\)
We'll primarily use the definition in order to help us prove the two theorems that follow.
Theorem
Provided \(t>1\):
\(\Gamma(t)=(t-1) \times \Gamma(t-1) \)
Proof
We'll useintegration by parts with:
\(u=y^{t-1}\) and \(dv=e^{-y}dy\)
to get:
\(du=(t-1)y^{t-2}\) and \(v=-e^{-y}\)
Then, the integration by parts gives us:
\(\Gamma(t)=\lim\limits_{b \to \infty} \left[-y^{t-1}e^{-y}\right]^{y=b}_{y=0} + (t-1)\int_0^\infty y^{t-2}e^{-y}dy\)
Evaluating at \(y=b\)and \(y=0\)for the first term, and using the definition of the gamma function (provided \(t-1>0\)) for the second term, we have:
\(\Gamma(t)=-\lim\limits_{b \to \infty} \left[\dfrac{b^{t-1}}{e^b}\right]+(t-1)\Gamma(t-1)\)
Now, if we were to be lazy, we would just wave our hands, and say that the first term goes to 0, and therefore:
\(\Gamma(t)=(t-1) \times \Gamma(t-1)\)
provided \(t>1\), as was to be proved.
Let's not be too lazy though! Taking the limit as \(b\)goes to infinity for that first term, we get infinity over infinity. Ugh! Maybe we should have left well enough alone! We can take the exponent and the natural log of the numerator without changing the limit. Doing so, we get:
\(-\lim\limits_{b \to \infty} \left[\dfrac{b^{t-1}}{e^b}\right] =-\lim\limits_{b \to \infty} \left\{\dfrac{\text{exp}[(t-1) \ln b]}{\text{exp}(b)}\right\}\)
Then, because both the numerator and denominator are exponents, we can write the limit as:
\(-\lim\limits_{b \to \infty} \left[\dfrac{b^{t-1}}{e^b}\right] =-\lim\limits_{b \to \infty}\{\text{exp}[(t-1) \ln b-b]\}\)
Manipulating the limit a bit more, so that we can easily apply L'Hôpital's Rule, we get:
\(-\lim\limits_{b \to \infty} \left[\dfrac{b^{t-1}}{e^b}\right] =-\lim\limits_{b \to \infty} \left\{\text{exp}\left[(t-1)b\left(\dfrac{ \ln b}{b}-1\right)\right]\right\}\)
Now, let's take the limit as \(b\)goes to infinity:
Okay, our proof is now officially complete! We have shown what we set out to show. Maybe next time, I'll just wave my hands when I need a limit to go to 0.
Theorem
If \(t=n\), a positive integer, then:
\(\Gamma(n)=(n-1)!\)
Proof
Using the previous theorem:
\begin{align} \Gamma(n) &= (n-1)\Gamma(n-1)\\ &= (n-1)(n-2)\Gamma(n-2)\\ &= (n-1)(n-2)(n-3)\cdots (2)(1)\Gamma(1) \end{align}
And, since by the definition of the gamma function:
\(\Gamma(1)=\int_0^\infty y^{1-1}e^{-y} dy=\int_0^\infty e^{-y} dy=1\)
we have:
\(\Gamma(n)=(n-1)!\)
as was to be proved.
15.6 - Gamma Properties
15.6 - Gamma PropertiesHere, after formally defining the gamma distribution (we haven't done that yet?!), we present and prove (well, sort of!) three key properties of the gamma distribution.
- Gamma Distribution
-
A continuous random variable \(X\) follows a gamma distribution with parameters \(\theta>0\) and \(\alpha>0\) if its probability density function is:
\(f(x)=\dfrac{1}{\Gamma(\alpha)\theta^\alpha} x^{\alpha-1} e^{-x/\theta}\)
for \(x>0\).
Before we get to the three theorems and proofs, two notes:
-
We consider \(\alpha>0\) a positive integer if the derivation of the p.d.f. is motivated by waiting times until α events. But the p.d.f. is actually a valid p.d.f. for any \(\alpha>0\) (since \(\Gamma(\alpha)\) is defined for all positive \(\alpha\)).
-
The gamma p.d.f. reaffirms that the exponential distribution is just a special case of the gamma distribution. That is, when you put \(\alpha=1\) into the gamma p.d.f., you get the exponential p.d.f.
Theorem
The moment generating function of a gamma random variable is:
\(M(t)=\dfrac{1}{(1-\theta t)^\alpha}\)
for \(t<\frac{1}{\theta}\).
Proof
By definition, the moment generating function \(M(t)\) of a gamma random variable is:
\(M(t)=E(e^{tX})=\int_0^\infty \dfrac{1}{\Gamma(\alpha)\theta^\alpha}e^{-x/\theta} x^{\alpha-1} e^{tx}dx\)
Collecting like terms, we get:
\(M(t)=E(e^{tX})=\int_0^\infty \dfrac{1}{\Gamma(\alpha)\theta^\alpha}e^{-x\left(\frac{1}{\theta}-t\right)} x^{\alpha-1} dx\)
Now, let's use the change of variable technique with:
\(y=x\left(\dfrac{1}{\theta}-t\right)\)
Rearranging, we get:
\(x=\dfrac{\theta}{1-\theta t}y\) and therefore \(dx=\dfrac{\theta}{1-\theta t}dy\)
Now, making the substitutions for \(x\) and \(dx\) into our integral, we get:
Theorem
The mean of a gamma random variable is:
\(\mu=E(X)=\alpha \theta\)
Proof
The proof is left for you as an exercise.
Theorem
The variance of a gamma random variable is:
\(\sigma^2=Var(X)=\alpha \theta^2\)
Proof
This proof is also left for you as an exercise.
15.7 - A Gamma Example
15.7 - A Gamma ExampleExample 15-4
Engineers designing the next generation of space shuttles plan to include two fuel pumps —one active, the other in reserve. If the primary pump malfunctions, the second is automatically brought on line. Suppose a typical mission is expected to require that fuel be pumped for at most 50 hours. According to the manufacturer's specifications, pumps are expected to fail once every 100 hours. What are the chances that such a fuel pump system would not remain functioning for the full 50 hours?
Solution
We are given that \(\lambda\), the average number of failures in a 100-hour interval is 1. Therefore, \(\theta\), the mean waiting time until the first failure is \(\dfrac{1}{\lambda}\), or 100 hours. Knowing that, let's now let \(Y\) denote the time elapsed until the \(\alpha\) = 2nd pump breaks down. Assuming the failures follow a Poisson process, the probability density function of \(Y\) is:
\(f_Y(y)=\dfrac{1}{100^2 \Gamma(2)}e^{-y/100} y^{2-1}=\dfrac{1}{10000}ye^{-y/100} \)
for \(y>0\). Therefore, the probability that the system fails to last for 50 hours is:
\(P(Y<50)=\int^{50}_0 \dfrac{1}{10000}ye^{-y/100} dy\)
Integrating that baby is going to require integration by parts. Let's let:
\(u=y\) and \(dv=e^{-y/100} \)
So that:
\(du=dy\) and \(v=-100e^{-y/100} \)
Now, for the integration:
15.8 - Chi-Square Distributions
15.8 - Chi-Square DistributionsChi-squared distributions are very important distributions in the field of statistics. As such, if you go on to take the sequel course, Stat 415, you will encounter the chi-squared distributions quite regularly. In this course, we'll focus just on introducing the basics of the distributions to you. In Stat 415, you'll see its many applications.
As it turns out, the chi-square distribution is just a special case of the gamma distribution! Let's take a look.
- Chi-square Distribution with \(r\) degrees of freedom
-
Let \(X\) follow a gamma distribution with \(\theta=2\) and \(\alpha=\frac{r}{2}\), where \(r\) is a positive integer. Then the probability density function of \(X\) is:
\(f(x)=\dfrac{1}{\Gamma (r/2) 2^{r/2}}x^{r/2-1}e^{-x/2}\)
for \(x>0\). We say that \(X\) follows a chi-square distribution with \(r\) degrees of freedom, denoted \(\chi^2(r)\) and read "chi-square-r."
There are, of course, an infinite number of possible values for \(r\), the degrees of freedom. Therefore, there are an infinite number of possible chi-square distributions. That is why (again!) the title of this page is called Chi-Square Distributions (with an s!), rather than Chi-Square Distribution (with no s)!
As the following theorems illustrate, the moment generating function, mean and variance of the chi-square distributions are just straightforward extensions of those for the gamma distributions.
Theorem
Let \(X\) be a chi-square random variable with \(r\) degrees of freedom. Then, the moment generating function of \(X\) is:
\(M(t)=\dfrac{1}{(1-2t)^{r/2}}\)
for \(t<\frac{1}{2}\).
Proof
The moment generating function of a gamma random variable is:
\(M(t)=\dfrac{1}{(1-\theta t)^\alpha}\)
The proof is therefore straightforward by substituting 2 in for \(\theta\) and \(\frac{r}{2}\) in for \(\alpha\).
Theorem
Let \(X\) be a chi-square random variable with \(r\) degrees of freedom. Then, the mean of \(X\) is:
\(\mu=E(X)=r\)
That is, the mean of \(X\) is the number of degrees of freedom.
Proof
The mean of a gamma random variable is:
\(\mu=E(X)=\alpha \theta\)
The proof is again straightforward by substituting 2 in for \(\theta\) and \(\frac{r}{2}\) in for \(\alpha\).
Theorem
Let \(X\) be a chi-square random variable with \(r\) degrees of freedom. Then, the variance of \(X\) is:
\(\sigma^2=Var(X)=2r\)
That is, the variance of \(X\) is twice the number of degrees of freedom.
Proof
The variance of a gamma random variable is:
\(\sigma^2=Var(X)=\alpha \theta^2\)
The proof is again straightforward by substituting 2 in for \(\theta\) and \(\frac{r}{2}\) in for \(\alpha\).
15.9 - The Chi-Square Table
15.9 - The Chi-Square TableOne of the primary ways that you will find yourself interacting with the chi-square distribution, primarily later in Stat 415, is by needing to know either a chi-square value or a chi-square probability in order to complete a statistical analysis. For that reason, we'll now explore how to use a typical chi-square table to look up chi-square values and/or chi-square probabilities. Let's start with two definitions.
Definition. Let \(\alpha\) be some probability between 0 and 1 (most often, a small probability less than 0.10). The upper \(100\alpha^{th}\) percentile of a chi-square distribution with \(r\) degrees of freedom is the value \(\chi^2_\alpha (r)\) such that the area under the curve and to the right of \(\chi^2_\alpha (r)\) is \(\alpha\):
The above definition is used, as is the one that follows, in Table IV, the chi-square distribution table in the back of your textbook.
Definition. Let \(\alpha\) be some probability between 0 and 1 (most often, a small probability less than 0.10). The \(100\alpha^{th}\) percentile of a chi-square distribution with \(r\) degrees of freedom is the value \(\chi^2_{1-\alpha} (r)\) such that the area under the curve and to the right of \(\chi^2_{1-\alpha} (r)\) is \(1-\alpha\):
With these definitions behind us, let's now take a look at the chi-square table in the back of your textbook.
Solution
In summary, here are the steps you should use in using the chi-square table to find a chi-square value:
- Find the row that corresponds to the relevant degrees of freedom, \(r\) .
- Find the column headed by the probability of interest... whether it's 0.01, 0.025, 0.05, 0.10, 0.90, 0.95, 0.975, or 0.99.
- Determine the chi-square value where the \(r\) row and the probability column intersect.
Now, at least theoretically, you could also use the chi-square table to find the probability associated with a particular chi-square value. But, as you can see, the table is pretty limited in that direction. For example, if you have a chi-square random variable with 5 degrees of freedom, you could only find the probabilities associated with the chi-square values of 0.554, 0.831, 1.145, 1.610, 9.236, 11.07, 12.83, and 15.09:
| P(X ≤ x) | ||||||||
| 0.010 | 0.025 | 0.050 | 0.100 | 0.900 | 0.950 | 0.975 | 0.990 | |
| r | x20.99(r) | x20.975(r) | x20.95(r) | x20.90(r) | x20.10(r) | x20.05(r) | x20.025(r) | x20.01(r) |
| 1 | 0.000 | 0.001 | 0.004 | 0.016 | 2.706 | 3.841 | 5.042 | 6.635 |
| 2 | 0.020 | 0.051 | 0.103 | 0.211 | 4.605 | 5.991 | 7.378 | 9.210 |
| 3 | 0.115 | 0.216 | 0.352 | 0.584 | 6.251 | 7.815 | 9.348 | 11.34 |
| 4 | 0.297 | 0.484 | 0.711 | 1.046 | 7.779 | 9.488 | 11.14 | 13.28 |
| 5 | 0.554 | 0.831 | 1.145 | 1.610 | 9.236 | 11.07 | 12.83 | 15.09 |
What would you do if you wanted to find the probability that a chi-square random variable with 5 degrees of freedom was less than 6.2, say? Well, the answer is, of course... statistical software, such as SAS or Minitab! For what we'll be doing in Stat 414 and 415, the chi-square table will (mostly) serve our purpose. Let's get a bit more practice now using the chi-square table.
Example 15-5
Let \(X\) be a chi-square random variable with 10 degrees of freedom. What is the upper fifth percentile?
Solution
The upper fifth percentile is the chi-square value x such that the probability to the right of \(x\) is 0.05, and therefore the probability to the left of \(x\) is 0.95. To find x using the chi-square table, we:
- Find \(r=10\) in the first column on the left.
- Find the column headed by \(P(X\le x)=0.95\).
Now, all we need to do is read the chi-square value where the \(r=10\) row and the \(P(X\le x)=0.95\) column intersect. What do you get?
| P(X ≤ x) | ||||||||
| 0.010 | 0.025 | 0.050 | 0.100 | 0.900 | 0.950 | 0.975 | 0.990 | |
| r | x20.99(r) | x20.975(r) | x20.95(r) | x20.90(r) | x20.10(r) | x20.05(r) | x20.025(r) | x20.01(r) |
| 1 | 0.000 | 0.001 | 0.004 | 0.016 | 2.706 | 3.841 | 5.042 | 6.635 |
| 2 | 0.020 | 0.051 | 0.103 | 0.211 | 4.605 | 5.991 | 7.378 | 9.210 |
| 3 | 0.115 | 0.216 | 0.352 | 0.584 | 6.251 | 7.815 | 9.348 | 11.34 |
| 4 | 0.297 | 0.484 | 0.711 | 1.046 | 7.779 | 9.488 | 11.14 | 13.28 |
| 5 | 0.554 | 0.831 | 1.145 | 1.610 | 9.236 | 11.07 | 12.83 | 15.09 |
| 6 | 0.872 | 1.237 | 1.635 | 2.204 | 10.64 | 12.59 | 14.45 | 16.81 |
| 7 | 1.239 | 1.690 | 2.167 | 2.833 | 12.02 | 14.07 | 16.01 | 18.48 |
| 8 | 1.646 | 2.180 | 2.733 | 3.490 | 13.36 | 15.51 | 17.54 | 20.09 |
| 9 | 2.088 | 2.700 | 3.325 | 4.168 | 14.68 | 16.92 | 19.02 | 21.67 |
| 10 | 2.558 | 3.247 | 3.940 | 4.865 | 15.99 | 18.31 | 20.48 | 23.21 |
| P(X ≤ x) | ||||||||
| 0.010 | 0.025 | 0.050 | 0.100 | 0.900 | 0.950 | 0.975 | 0.990 | |
| r | x20.99(r) | x20.975(r) | x20.95(r) | x20.90(r) | x20.10(r) | x20.05(r) | x20.025(r) | x20.01(r) |
| 1 | 0.000 | 0.001 | 0.004 | 0.016 | 2.706 | 3.841 | 5.042 | 6.635 |
| 2 | 0.020 | 0.051 | 0.103 | 0.211 | 4.605 | 5.991 | 7.378 | 9.210 |
| 3 | 0.115 | 0.216 | 0.352 | 0.584 | 6.251 | 7.815 | 9.348 | 11.34 |
| 4 | 0.297 | 0.484 | 0.711 | 1.046 | 7.779 | 9.488 | 11.14 | 13.28 |
| 5 | 0.554 | 0.831 | 1.145 | 1.610 | 9.236 | 11.07 | 12.83 | 15.09 |
| 6 | 0.872 | 1.237 | 1.635 | 2.204 | 10.64 | 12.59 | 14.45 | 16.81 |
| 7 | 1.239 | 1.690 | 2.167 | 2.833 | 12.02 | 14.07 | 16.01 | 18.48 |
| 8 | 1.646 | 2.180 | 2.733 | 3.490 | 13.36 | 15.51 | 17.54 | 20.09 |
| 9 | 2.088 | 2.700 | 3.325 | 4.168 | 14.68 | 16.92 | 19.02 | 21.67 |
| 10 | 2.558 | 3.247 | 3.940 | 4.865 | 15.99 | 18.31 | 20.48 | 23.21 |
The table tells us that the upper fifth percentile of a chi-square random variable with 10 degrees of freedom is 18.31.
What is the tenth percentile?
Solution
The tenth percentile is the chi-square value \(x\) such that the probability to the left of \(x\) is 0.10. To find x using the chi-square table, we:
- Find \(r=10\) in the first column on the left.
- Find the column headed by \(P(X\le x)=0.10\).
Now, all we need to do is read the chi-square value where the \(r=10\) row and the \(P(X\le x)=0.10\) column intersect. What do you get?
| P(X ≤ x) | ||||||||
| 0.010 | 0.025 | 0.050 | 0.100 | 0.900 | 0.950 | 0.975 | 0.990 | |
| r | x20.99(r) | x20.975(r) | x20.95(r) | x20.90(r) | x20.10(r) | x20.05(r) | x20.025(r) | x20.01(r) |
| 1 | 0.000 | 0.001 | 0.004 | 0.016 | 2.706 | 3.841 | 5.042 | 6.635 |
| 2 | 0.020 | 0.051 | 0.103 | 0.211 | 4.605 | 5.991 | 7.378 | 9.210 |
| 3 | 0.115 | 0.216 | 0.352 | 0.584 | 6.251 | 7.815 | 9.348 | 11.34 |
| 4 | 0.297 | 0.484 | 0.711 | 1.046 | 7.779 | 9.488 | 11.14 | 13.28 |
| 5 | 0.554 | 0.831 | 1.145 | 1.610 | 9.236 | 11.07 | 12.83 | 15.09 |
| 6 | 0.872 | 1.237 | 1.635 | 2.204 | 10.64 | 12.59 | 14.45 | 16.81 |
| 7 | 1.239 | 1.690 | 2.167 | 2.833 | 12.02 | 14.07 | 16.01 | 18.48 |
| 8 | 1.646 | 2.180 | 2.733 | 3.490 | 13.36 | 15.51 | 17.54 | 20.09 |
| 9 | 2.088 | 2.700 | 3.325 | 4.168 | 14.68 | 16.92 | 19.02 | 21.67 |
| 10 | 2.558 | 3.247 | 3.940 | 4.865 | 15.99 | 18.31 | 20.48 | 23.21 |
| P(X ≤ x) | ||||||||
| 0.010 | 0.025 | 0.050 | 0.100 | 0.900 | 0.950 | 0.975 | 0.990 | |
| r | x20.99(r) | x20.975(r) | x20.95(r) | x20.90(r) | x20.10(r) | x20.05(r) | x20.025(r) | x20.01(r) |
| 1 | 0.000 | 0.001 | 0.004 | 0.016 | 2.706 | 3.841 | 5.042 | 6.635 |
| 2 | 0.020 | 0.051 | 0.103 | 0.211 | 4.605 | 5.991 | 7.378 | 9.210 |
| 3 | 0.115 | 0.216 | 0.352 | 0.584 | 6.251 | 7.815 | 9.348 | 11.34 |
| 4 | 0.297 | 0.484 | 0.711 | 1.046 | 7.779 | 9.488 | 11.14 | 13.28 |
| 5 | 0.554 | 0.831 | 1.145 | 1.610 | 9.236 | 11.07 | 12.83 | 15.09 |
| 6 | 0.872 | 1.237 | 1.635 | 2.204 | 10.64 | 12.59 | 14.45 | 16.81 |
| 7 | 1.239 | 1.690 | 2.167 | 2.833 | 12.02 | 14.07 | 16.01 | 18.48 |
| 8 | 1.646 | 2.180 | 2.733 | 3.490 | 13.36 | 15.51 | 17.54 | 20.09 |
| 9 | 2.088 | 2.700 | 3.325 | 4.168 | 14.68 | 16.92 | 19.02 | 21.67 |
| 10 | 2.558 | 3.247 | 3.940 | 4.865 | 15.99 | 18.31 | 20.48 | 23.21 |
The table tells us that the tenth percentile of a chi-square random variable with 10 degrees of freedom is 4.865.
What is the probability that a chi-square random variable with 10 degrees of freedom is greater than 15.99?
Solution
There I go... just a minute ago, I said that the chi-square table isn't very helpful in finding probabilities, then I turn around and ask you to use the table to find a probability! Doing it at least once helps us make sure that we fully understand the table. In this case, we are going to need to read the table "backwards." To find the probability, we:
- Find \(r=10\) in the first column on the left.
- Find the value 15.99 in the \(r=10\) row.
- Read the probability headed by the column in which the 15.99 falls.
What do you get?
| P(X ≤ x) | ||||||||
| 0.010 | 0.025 | 0.050 | 0.100 | 0.900 | 0.950 | 0.975 | 0.990 | |
| r | x20.99(r) | x20.975(r) | x20.95(r) | x20.90(r) | x20.10(r) | x20.05(r) | x20.025(r) | x20.01(r) |
| 1 | 0.000 | 0.001 | 0.004 | 0.016 | 2.706 | 3.841 | 5.042 | 6.635 |
| 2 | 0.020 | 0.051 | 0.103 | 0.211 | 4.605 | 5.991 | 7.378 | 9.210 |
| 3 | 0.115 | 0.216 | 0.352 | 0.584 | 6.251 | 7.815 | 9.348 | 11.34 |
| 4 | 0.297 | 0.484 | 0.711 | 1.046 | 7.779 | 9.488 | 11.14 | 13.28 |
| 5 | 0.554 | 0.831 | 1.145 | 1.610 | 9.236 | 11.07 | 12.83 | 15.09 |
| 6 | 0.872 | 1.237 | 1.635 | 2.204 | 10.64 | 12.59 | 14.45 | 16.81 |
| 7 | 1.239 | 1.690 | 2.167 | 2.833 | 12.02 | 14.07 | 16.01 | 18.48 |
| 8 | 1.646 | 2.180 | 2.733 | 3.490 | 13.36 | 15.51 | 17.54 | 20.09 |
| 9 | 2.088 | 2.700 | 3.325 | 4.168 | 14.68 | 16.92 | 19.02 | 21.67 |
| 10 | 2.558 | 3.247 | 3.940 | 4.865 | 15.99 | 18.31 | 20.48 | 23.21 |
| P(X ≤ x) | ||||||||
| 0.010 | 0.025 | 0.050 | 0.100 | 0.900 | 0.950 | 0.975 | 0.990 | |
| r | x20.99(r) | x20.975(r) | x20.95(r) | x20.90(r) | x20.10(r) | x20.05(r) | x20.025(r) | x20.01(r) |
| 1 | 0.000 | 0.001 | 0.004 | 0.016 | 2.706 | 3.841 | 5.042 | 6.635 |
| 2 | 0.020 | 0.051 | 0.103 | 0.211 | 4.605 | 5.991 | 7.378 | 9.210 |
| 3 | 0.115 | 0.216 | 0.352 | 0.584 | 6.251 | 7.815 | 9.348 | 11.34 |
| 4 | 0.297 | 0.484 | 0.711 | 1.046 | 7.779 | 9.488 | 11.14 | 13.28 |
| 5 | 0.554 | 0.831 | 1.145 | 1.610 | 9.236 | 11.07 | 12.83 | 15.09 |
| 6 | 0.872 | 1.237 | 1.635 | 2.204 | 10.64 | 12.59 | 14.45 | 16.81 |
| 7 | 1.239 | 1.690 | 2.167 | 2.833 | 12.02 | 14.07 | 16.01 | 18.48 |
| 8 | 1.646 | 2.180 | 2.733 | 3.490 | 13.36 | 15.51 | 17.54 | 20.09 |
| 9 | 2.088 | 2.700 | 3.325 | 4.168 | 14.68 | 16.92 | 19.02 | 21.67 |
| 10 | 2.558 | 3.247 | 3.940 | 4.865 | 15.99 | 18.31 | 20.48 | 23.21 |
The table tells us that the probability that a chi-square random variable with 10 degrees of freedom is less than 15.99 is 0.90. Therefore, the probability that a chi-square random variable with 10 degrees of freedom is greater than 15.99 is 1−0.90, or 0.10.
15.10 - Trick To Avoid Integration
15.10 - Trick To Avoid IntegrationSometimes taking the integral is not an easy task. We do have some tools, however, to help avoid some of them. Let's take a look at an example.
Suppose we have a random variable, \(X\), that has a Gamma distribution and we want to find the Moment Generating function of \(X\), \(M_X(t)\). There is an example of how to compute this in the notes but let's try it another way.
\(\begin{align*} M_X(t)&=\int_0^\infty \frac{1}{\Gamma(\alpha)\beta^\alpha} x^{\alpha-1}e^{-x/\beta}e^{tx}dx\\ & = \int_0^\infty \frac{1}{\Gamma(\alpha)\beta^\alpha} x^{\alpha-1}e^{-x\left(\frac{1}{\beta}-t\right)}dx \end{align*}\)
Let's rewrite this integral, taking out the constants for now and rewriting the exponent term.
\(\begin{align*} M_X(t)&= \frac{1}{\Gamma(\alpha)\beta^\alpha}\int_0^\infty x^{\alpha-1}e^{-x\left(\frac{1}{\beta}-t\right)}dx\\ & =\frac{1}{\Gamma(\alpha)\beta^\alpha}\int_0^\infty x^{\alpha-1}e^{-x\left(\frac{1-\beta t}{\beta}\right)}dx\\ & = \frac{1}{\Gamma(\alpha)\beta^\alpha}\int_0^\infty x^{\alpha-1}e^{-x/\left(\frac{\beta}{1-\beta t}\right)}dx\\ & = \frac{1}{\Gamma(\alpha)\beta^\alpha}\int_0^\infty g(x)dx \end{align*}\)
When we rewrite it this way, the term under the integral, \(g(x)\), looks almost like a Gamma density function with parameters \(\alpha\) and \(\beta^*=\dfrac{\beta}{1-\beta t}\). The only issues that we need to take care of are the constants in front of the integral and the constants to make \(g(x)\) a gamma density function.
To make \(g(x)\) a Gamma density function, we need the constants. Therefore, we need a \(\dfrac{1}{\Gamma(\alpha)}\) term and a \(\dfrac{1}{(\beta^*)^\alpha}\) term. We already have the first term, so lets rewrite the function.
\(M_X(t)=\frac{1}{\beta^\alpha}\int_0^\infty \frac{1}{\Gamma(\alpha)}x^{\alpha-1}e^{-x/\left(\frac{\beta}{1-\beta t}\right)}dx\)
All that is left is the \(\dfrac{1}{(\beta^*)^\alpha}\).
\(\frac{1}{(\beta^*)^\alpha}=\frac{1}{\left(\frac{\beta}{1-\beta t}\right)^\alpha}=\frac{\left(1-\beta t\right)^\alpha}{\beta^\alpha}\)
We have the denominator term already. Lets rewrite just for clarity.
\(M_X(t)=\int_0^\infty \frac{1}{\Gamma(\alpha)\beta^\alpha}x^{\alpha-1}e^{-x/\left(\frac{\beta}{1-\beta t}\right)}dx\)
Since \(\dfrac{1}{(\beta^*)^\alpha}=\dfrac{\left(1-\beta t\right)^\alpha}{\beta^\alpha}\), we need only to include the \((1-\beta t) ^\alpha\) term. If we include the term in the integral, we have to multiply by one. Therefore,
\( \begin{align*} & M_X(t)=\left(\frac{(1-\beta t)^\alpha}{(1-\beta t)^\alpha}\right)\int_0^\infty \frac{1}{\Gamma(\alpha)\beta^\alpha}x^{\alpha-1}e^{-x/\left(\frac{\beta}{1-\beta t}\right)}dx\\ & = \left(\frac{1}{(1-\beta t)^\alpha}\right)\int_0^\infty \frac{(1-\beta t)^\alpha}{\Gamma(\alpha)\beta^\alpha}x^{\alpha-1}e^{-x/\left(\frac{\beta}{1-\beta t}\right)}dx\\ & \left(\frac{1}{(1-\beta t)^\alpha}\right)\int_0^\infty \frac{1}{\Gamma(\alpha)\left(\frac{\beta}{1-\beta t}\right)^\alpha}x^{\alpha-1}e^{-x/\left(\frac{\beta}{1-\beta t}\right)}dx\\ & \left(\frac{1}{(1-\beta t)^\alpha}\right)\int_0^\infty h(x) dx \end{align*}\)
Therefore, \(h(x)\) is now a Gamma density function with parameters \(\alpha\) and \(\beta^*=\dfrac{\beta}{1-\beta t}\). And, since \(h(x)\) is a pdf and we are integrating over the whole space, \(x\ge 0\), then \(\int_0^\infty h(x)dx=1\). If the integral is equal to 1 based on the definition of a pdf, we are left with:
\(M_X(t)=\dfrac{1}{(1-\beta t)^\alpha}\left(1\right)=\dfrac{1}{(1-\beta t)^\alpha}\)
From the notes and the text, you can see that the moment generating function calculated above is exactly what we were supposed to get.
Just to summarize what we did here. We did not actually calculate the integral. We used algebra to manipulate the function to use the definition of a pdf. I find that after practice, this method is a lot quicker for me than doing the integrals.
Additional Practice Problems
These problems are not due for homework.
-
Find \(E(X)\) using the method above.
\(\begin{align*} E(X)&=\int_0^\infty x\frac{1}{\Gamma(\alpha)\beta^\alpha}x^{\alpha-1}e^{-x/\beta}dx\\[5 pt] &=\frac{1}{\Gamma(\alpha)\beta^{\alpha}}\int_0^\infty x^{\alpha}e^{-x/\beta}dx\\[5 pt] &=\left(\frac{1}{\Gamma(\alpha)\beta^{\alpha}}\right)\left(\frac{\Gamma(\alpha+1)\beta^{\alpha+1}}{\Gamma(\alpha+1)\beta^{\alpha+1}}\right)\int_0^\infty x^{\alpha}e^{-x/\beta}dx\\[5 pt] &=\left(\frac{\Gamma(\alpha+1)\beta^{\alpha+1}}{\Gamma(\alpha)\beta^{\alpha}}\right)\int_0^\infty \left(\frac{1}{\Gamma(\alpha+1)\beta^{\alpha+1}}\right) x^{\alpha}e^{-x/\beta}dx \\[5 pt] &=\frac{\Gamma(\alpha+1)\beta^{\alpha+1}}{\Gamma(\alpha)\beta^{\alpha}}(1)\\[5 pt] &=\frac{\alpha\Gamma(\alpha)\beta}{\Gamma(\alpha)}\\[5 pt]&=\alpha\beta \end{align*}\)
-
Find \(E(X^2)\) using the method above.
\(\begin{align*} E(X^2)&=\int_0^\infty x^2\frac{1}{\Gamma(\alpha)\beta^\alpha}x^{\alpha-1}e^{-x/\beta}dx\\[5 pt]&=\frac{1}{\Gamma(\alpha)\beta^{\alpha}}\int_0^\infty x^{\alpha+1}e^{-x/\beta}dx\\[5 pt]&=\left(\frac{1}{\Gamma(\alpha)\beta^{\alpha}}\right)\left(\frac{\Gamma(\alpha+2)\beta^{\alpha+2}}{\Gamma(\alpha+2)\beta^{\alpha+2}}\right)\int_0^\infty x^{\alpha+1}e^{-x/\beta}dx\\[5 pt]&=\left(\frac{\Gamma(\alpha+2)\beta^{\alpha+2}}{\Gamma(\alpha)\beta^{\alpha}}\right)\int_0^\infty \left(\frac{1}{\Gamma(\alpha+2)\beta^{\alpha+2}}\right) x^{\alpha+1}e^{-x/\beta}dx\\[5 pt]& =\frac{\Gamma(\alpha+2)\beta^{\alpha+2}}{\Gamma(\alpha)\beta^{\alpha}}(1)\\[5 pt]&=\frac{(\alpha+1)\Gamma(\alpha+1)\beta^2}{\Gamma(\alpha)}\\[5 pt]&=\alpha(\alpha+1)\beta^2 \end{align*}\)
Lesson 16: Normal Distributions
Lesson 16: Normal DistributionsOverview
In this lesson, we'll investigate one of the most prevalent probability distributions in the natural world, namely the normal distribution. Just as we have for other probability distributions, we'll explore the normal distribution's properties, as well as learn how to calculate normal probabilities.
Objectives
- To define the probability density function of a normal random variable.
- To learn the characteristics of a typical normal curve.
- To learn how to transform a normal random variable \(X\) into the standard normal random variable \(Z\).
- To learn how to calculate the probability that a normal random variable \(X\) falls between two values \(a\) and \(b\), below a value \(c\), or above a value \(d\).
- To learn how to read standard normal probability tables.
- To learn how to find the value \(x\) associated with a cumulative normal probability.
- To explore the key properties, such as the moment-generating function, mean and variance, of a normal random variable.
- To investigate the relationship between the standard normal random variable and a chi-square random variable with one degree of freedom.
- To learn how to interpret a \(Z\)-value.
- To learn why the Empirical Rule holds true.
- To understand the steps involved in each of the proofs in the lesson.
- To be able to apply the methods learned in the lesson to new problems.
16.1 - The Distribution and Its Characteristics
16.1 - The Distribution and Its Characteristics- Normal Distribution
-
The continuous random variable \(X\) follows a normal distribution if its probability density function is defined as:
\(f(x)=\dfrac{1}{\sigma \sqrt{2\pi}} \text{exp}\left\{-\dfrac{1}{2} \left(\dfrac{x-\mu}{\sigma}\right)^2\right\}\)
for \(-\infty<x<\infty\), \(-\infty<\mu<\infty\), and \(0<\sigma<\infty\). The mean of \(X\) is \(\mu\) and the variance of \(X\) is \(\sigma^2\). We say \(X\sim N(\mu, \sigma^2)\).
With a first exposure to the normal distribution, the probability density function in its own right is probably not particularly enlightening. Let's take a look at an example of a normal curve, and then follow the example with a list of the characteristics of a typical normal curve.
Example 16-1
Let \(X\) denote the IQ (as determined by the Stanford-Binet Intelligence Quotient Test) of a randomly selected American. It has long been known that \(X\) follows a normal distribution with mean 100 and standard deviation of 16. That is, \(X\sim N(100, 16^2)\). Draw a picture of the normal curve, that is, the distribution, of \(X\).
Note that when drawing the above curve, I said "now what a standard normal curve looks like... it looks something like this." It turns out that the term "standard normal curve" actually has a specific meaning in the study of probability. As we'll soon see, it represents the case in which the mean \(\mu\) equals 0 and the standard deviation σ equals 1. So as not to cause confusion, I wish I had said "now what a typical normal curve looks like...." Anyway, on to the characteristics of all normal curves!
Characteristics of a Normal Curve
It is the following known characteristics of the normal curve that directed me in drawing the curve as I did so above.
-
All normal curves are bell-shaped with points of inflection at \(\mu\pm \sigma\).
ProofThe proof is left for you as an exercise
-
All normal curves are symmetric about the mean \(\mu\).
ProofAll normal curves are symmetric about the mean \(\mu\), because \(f(\mu+x)=f(\mu-x)\) for all \(x\). That is:
\(f(\mu+x)=\dfrac{1}{\sigma \sqrt{2\pi}} \text{exp}\left\{-\dfrac{1}{2} \left(\dfrac{x+\mu-\mu}{\sigma}\right)^2\right\} =\dfrac{1}{\sigma \sqrt{2\pi}} \text{exp}\left\{-\dfrac{1}{2} \left(\dfrac{x}{\sigma}\right)^2\right\}\)
equals:
\(f(\mu-x)=\dfrac{1}{\sigma \sqrt{2\pi}} \text{exp}\left\{-\dfrac{1}{2} \left(\dfrac{\mu-x-\mu}{\sigma}\right)^2\right\} =\dfrac{1}{\sigma \sqrt{2\pi}} \text{exp}\left\{-\dfrac{1}{2} \left(\dfrac{-x}{\sigma}\right)^2\right\}=\dfrac{1}{\sigma \sqrt{2\pi}} \text{exp}\left\{-\dfrac{1}{2} \left(\dfrac{x}{\sigma}\right)^2\right\}\)
Therefore, by the definition of symmetry, the normal curve is symmetric about the mean \(\mu\).
-
The area under an entire normal curve is 1.
ProofWe prove this later on the Normal Properties page. -
All normal curves are positive for all \(x\). That is, \(f(x)>0\) for all \(x\).
ProofThe standard deviation \(\sigma\) is defined to be positive. The square root of \(2\pi\) is positive. And, the natural exponential function is positive. When you multiply positive terms together, you, of course, get a positive number.
-
The limit of \(f(x)\) as \(x\) goes to infinity is 0, and the limit of \(f(x)\) as \(x\) goes to negative infinity is 0. That is:
\(\lim\limits_{x\to \infty} f(x)=0\) and \(\lim\limits_{x\to -\infty} f(x)=0\)
ProofThe function \(f(x)\) depends on \(x\) only through the natural exponential function \(\exp[-x^2]\), which is known to approach 0 as \(x\) approaches infinity or negative infinity.
-
The height of any normal curve is maximized at \(x=\mu\).
ProofUsing what we know from our calculus studies, to find the point at which the maximum occurs, we must differentiate \(f(x)\) with respect to \(x\) and solve for \(x\) to find the maximum. Because our \(f(x)\) contains the natural exponential function, however, it is easier to take the derivative of the natural log of \(f(x)\) with respect to \(x\) and solve for \(x\) to find the maximum. [The maximum of \(f(x)\) is the same as the maximum of the natural log of \(f(x)\), because \(\log_e(x)\) is an increasing function of \(x\). That is, \(x_1<x_2\) implies that \(\log_e(x_1)<\log_e(x_2)\). Therefore, \(f(x_1)<f(x_2)\) implies \(\log_e(f(x_1))<\log_e(f(x_2))\).] That said, taking the natural log of \(f(x)\), we get:
\(\text{log}_e (f(x))=\text{log}\left(\dfrac{1}{\sigma \sqrt{2\pi}} \right)-\dfrac{1}{2\sigma^2}(x-\mu)^2\)
Taking the derivative of \(\log_e(f(x))\) with respect to \(x\), we get:
\(\dfrac{d\text{log}f(x)}{dx}=-\dfrac{1}{2\sigma^2}\cdot 2(x-\mu)\)
Now, setting the derivative of \(\log_e(f(x))\) to 0:
\(\dfrac{d\text{log}f(x)}{dx}=-\dfrac{1}{2\sigma^2}\cdot 2(x-\mu) \stackrel{\equiv}{\scriptscriptstyle{SET}} 0\)
and solving for \(x\), we get that \(x=\mu\). Taking the second derivative of \(\log_e(f(x))\) with respect to \(x\), we get:
\(\dfrac{d^2\text{log}f(x)}{dx^2}=-\dfrac{1}{\sigma^2}\)
Because the second derivative of \(\log_e(f(x))\) is negative (for all \(x\), in fact), the point \(x=\mu\) is deemed a local maximum.
-
The shape of any normal curve depends on its mean \(\mu\) and standard deviation \(\sigma\).
ProofGiven that the curve \(f(x)\) depends only on \(x\) and the two parameters \(\mu\) and \(\sigma\), the claimed characteristic is quite obvious. An example is perhaps more interesting than the proof. Here is a picture of three superimposed normal curves —one of a \(N(0,9)\) curve, one of a \(N(0, 16)\) curve, and one of a \(N(1, 9)\) curve:
As claimed, the shapes of the three curves differ, as the means \(\mu\) and standard deviations \(\sigma\) differ.
16.2 - Finding Normal Probabilities
16.2 - Finding Normal ProbabilitiesExample 16-2
Let \(X\) equal the IQ of a randomly selected American. Assume \(X\sim N(100, 16^2)\). What is the probability that a randomly selected American has an IQ below 90?
Solution
As is the case with all continuous distributions, finding the probability involves finding the area under the curve and to the left of the line \(x=90\):
That is:
\(P(X \leq 90)=F(90)=\int^{90}_{-\infty} \dfrac{1}{16\sqrt{2\pi}}\text{exp}\left\{-\dfrac{1}{2}\left(\dfrac{x-100}{16}\right)^2\right\} dx\)
There's just one problem... it is not possible to integrate the normal p.d.f. That is, no simple expression exists for the antiderivative. We can only approximate the integral using numerical analysis techniques. So, all we need to do is find a normal probability table for a normal distribution with mean \(\mu=100\) and standard deviation \(\sigma=16\). Aw, geez, there'd have to be an infinite number of normal probability tables. That strategy isn't going to work! Aha! The cumulative probabilities have been tabled for the \(N(0,1)\) distribution. All we need to do is transform our \(N(100, 16^2)\) distribution to a \(N(0, 1)\) distribution and then use the cumulative probability table for the \(N(0,1)\) distribution to calculate our desired probability. The theorem that follows tells us how to make the necessary transformation.
If \(X\sim N(\mu, \sigma^2)\), then:
\(Z=\dfrac{X-\mu}{\sigma}\)
follows the \(N(0,1)\) distribution, which is called the standardized (or standard) normal distribution.
Proof
We need to show that the random variable \(Z\) follows a \(N(0,1)\) distribution. So, let's find the cumulative distribution function \(F(z)\), which is also incidentally referred to as \(\Phi(z)\) in the standard normal case (that's the greek letter phi, read "fee"):
\(F(z)=\Phi(z)=P(Z\leq z)=P \left(\dfrac{X-\mu}{\sigma} \leq z \right)\)
which, by rearranging and using the normal p.d.f., equals:
\(F(z)=P(X\leq \mu+z\sigma)=\int^{\mu+z\sigma}_{-\infty} \dfrac{1}{\sigma \sqrt{2\pi}} \text{exp}\left\{-\dfrac{1}{2} \left(\dfrac{x-\mu}{\sigma}\right)^2\right\} \)
To perform the integration, let's use the change of variable technique with:
\(w=\dfrac{x-\mu}{\sigma}\)
so that:
\(x = \sigma(w) + \mu \) and \(dx = \sigma dw\)
Now for the endpoints of the integral: if \(x=-\infty\), then \(w\) also equals \(-\infty\); and if \(x=\mu+z\sigma\), then \(w=\frac{\mu+z\sigma -\mu}{\sigma}\). Therefore, upon making all of the substitutions for \(x, w\), and \(dx\), our integration looks like this:
\(F(z)=\int^z_{-\infty}\dfrac{1}{\sigma \sqrt{2\pi}} \text{exp}\left\{-\dfrac{1}{2} w^2\right\} \sigma dw\)
And since the \(\sigma\) in the denominator cancels out the \(\sigma\) in the numerator, we get:
\(F(z)=\int^z_{-\infty}\dfrac{1}{\sqrt{2\pi}} \text{exp}\left\{-\dfrac{1}{2} w^2\right\} dw\)
We should now recognize that as the cumulative distribution of a normal random variable with mean \(\mu=0\) and standard deviation \(\sigma=1\). Our proof is complete.
The theorem leads us to the following strategy for finding probabilities \(P(z<X<b)\) when \(a\) and \(b\) are constants, and \(X\) is a normal random variable with mean \(\mu\) and standard deviation \(\sigma\):
-
1) Specify the desired probability in terms of \(X\).
-
2) Transform \(X, a\), and \(b\), by:
\(Z=\dfrac{X-\mu}{\sigma}\)
-
3) Use the standard normal \(N(0,1)\) table, typically referred to as the \(Z\)-table, to find the desired probability.
Reading \(Z\)-tables
Standard normal, or \(Z\)-tables, can take a number of different forms. There are two standard normal tables, Table Va and Table Vb, in the back of our textbook. Table Va gives the cumulative probabilities for \(Z\)-values, to two decimal places, between 0.00 and 3.09. Here's what the top of Table Va looks like:
\begin{aligned} P(Z \leq z)=& \Phi(z)=\int_{-\infty}^{z} \frac{1}{\sqrt{2 \pi}} e^{-w^{2} / 2} d w \\ \Phi(-z) &=1-\Phi(z) \end{aligned}
| z | 0.00 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.0 | 0.5000 | 0.5040 | 0.5080 | 0.5120 | 0.5160 | 0.5199 | 0.5239 | 0.5279 | 0.5319 | 0.5359 |
| 0.1 | 0.5398 | 0.5438 | 0.5478 | 0.5517 | 0.5557 | 0.5596 | 0.5636 | 0.5675 | 0.5714 | 0.5753 |
| 0.2 | 0.5793 | 0.5832 | 0.5871 | 0.5910 | 0.5948 | 0.5987 | 0.6026 | 0.6064 | 0.6103 | 0.6141 |
| 0.3 | 0.6179 | 0.6217 | 0.6255 | 0.6293 | 0.6310 | 0.6368 | 0.6406 | 0.6443 | 0.6480 | 0.6517 |
| 0.4 | 0.6554 | 0.6591 | 0.6628 | 0.6664 | 0.6700 | 0.6736 | 0.6772 | 0.6808 | 0.6844 | 0.6879 |
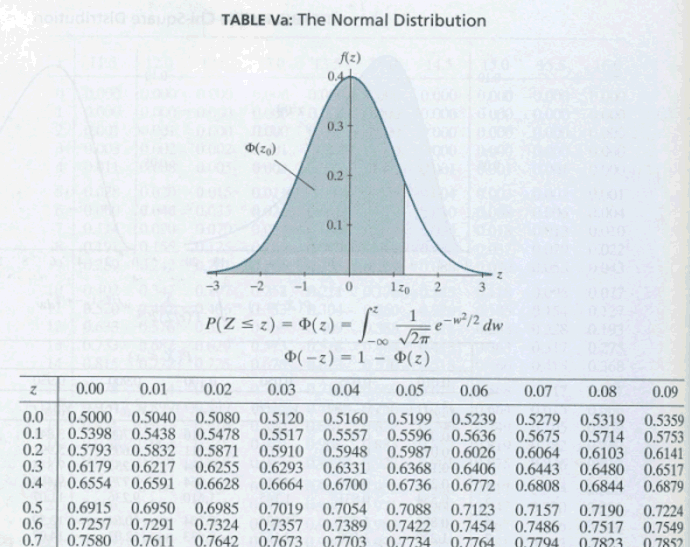
For example, you could use Table Va to find probabilities such as \(P(Z\le 0.01), P(Z\le 1.23)\), or \(P(Z\le 2.98)\). Table Vb, on the other hand, gives probabilities in the upper tail of the standard normal distribution. Here's what the top of Table Vb looks like:
\(P(Z > z_\alpha) = \alpha \)
\(P(Z > z) = 1 - \Phi(z) = \Phi(-z)\)
| \(z_\alpha\) | 0.00 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.0 | 0.5000 | 0.4960 | 0.4920 | 0.4880 | 0.4840 | 0.4801 | 0.4761 | 0.4721 | 0.4681 | 0.4641 |
| 0.1 | 0.4602 | 0.4562 | 0.4522 | 0.4483 | 0.4443 | 0.4404 | 0.4364 | 0.4325 | 0.4286 | 0.4247 |
| 0.2 | 0.4207 | 0.4168 | 0.4129 | 0.4090 | 0.4520 | 0.4013 | 0.3974 | 0.3936 | 0.3897 | 0.3859 |
| 0.3 | 0.3821 | 0.3783 | 0.3745 | 0.3707 | 0.3669 | 0.3632 | 0.3594 | 0.3570 | 0.3557 | 0.3483 |
| 0.4 | 0.3446 | 0.3409 | 0.3372 | 0.3336 | 0.3300 | 0.3264 | 0.3228 | 0.3192 | 0.3192 | 0.3121 |
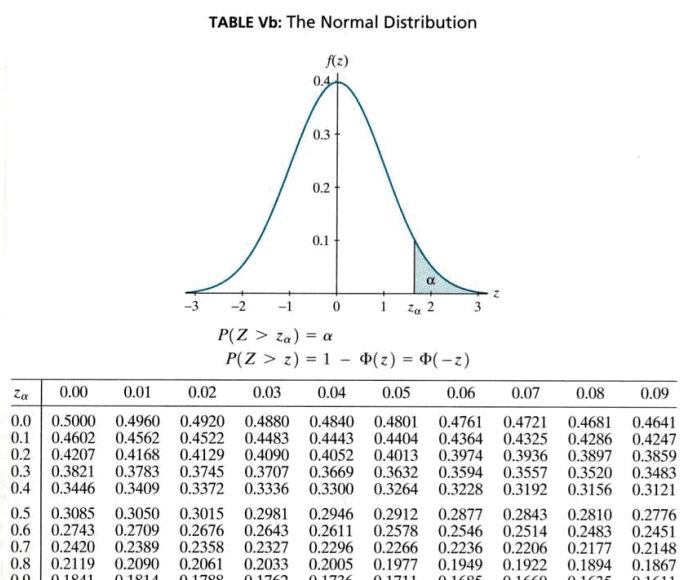
That is, for \(Z\)-values, to two decimal places, between 0.00 and 3.49, we can use Table Vb to find probabilities such as \(P(Z>0.12), P(Z>1.96)\), and \(P(Z>3.32)\).
Now, we just need to learn how to read the probabilities off of each of the tables. First Table Va:
And, then Table Vb:
Now we know how to read the given \(Z\)-tables. Now, we just need to work with some real examples to see that finding probabilities associated with a normal random variable usually involves rewriting the problems just a bit in order to get them to "fit" with the available \(Z\)-tables.
Example 16-2 Continued
Let \(X\) equal the IQ of a randomly selected American. Assume \(X\sim N(100, 16^2)\). What is the probability that a randomly selected American has an IQ below 90?
Answer
Whenever I am faced with finding a normal probability, I always always always draw a picture of the probability I am trying to find. Then, the problem usually just solves itself... oh, how we wish:
So, we just found that the desired probability, that is, that the probability that a randomly selected American has an IQ below 90 is 0.2643. (If you haven't already, you might want to make sure that you can independently read that probability off of Table Vb.)
Now, although I used Table Vb in finding our desired probability, it is worth mentioning that I could have alternatively used Table Va. How's that? Well:
\(P(X<90)=P(Z<-0.63)=P(Z>0.63)=1-P(Z<0.63)\)
where the first equality comes from the transformation from \(X\) to \(Z\), the second equality comes from the symmetry of the normal distribution, and the third equality comes from the rule of complementary events. Using Table Va to look up \(P(Z<0.63)\), we get 0.7357. Therefore,
\(P(X<90)=1-P(Z<0.63)=1-0.7357=0.2643\)
We should, of course, be reassured that our logic produced the same answer regardless of the method used! That's always a good thing!
What is the probability that a randomly selected American has an IQ above 140?
Answer
Again, I am going to solve this problem by drawing a picture:
So, we just found that the desired probability, that is, that the probability that a randomly selected American has an IQ above 140 is 0.0062. (Again, if you haven't already, you might want to make sure that you can independently read that probability off of Table Vb.)
We again could have alternatively used Table Va to find our desired probability:
\(P(X>140)=P(Z>2.50)=1-P(Z<2.50\)
where the first equality comes from the transformation from \(X\) to \(Z\), and the second equality comes from the rule of complementary events. Using Table Va to look up \(P(Z<2.5)\), we get 0.9938. Therefore,
\(P(X>140)=1-P(Z<2.50)=1-0.9938=0.0062\)
Again, we arrived at the same answer using two different methods.
What is the probability that a randomly selected American has an IQ between 92 and 114?
Answer
Again, I am going to solve this problem by drawing a picture:
So, we just found that the desired probability, that is, that the probability that a randomly selected American has an IQ between 92 and 114 is 0.5021. (Again, if you haven't already, you might want to make sure that you can independently read the probabilities that we used to get the answer from Tables Va and Vb.)
The previous three examples have illustrated each of the three possible normal probabilities you could be faced with finding —below some number, above some number, and between two numbers. Once you have mastered each case, then you should be able to find any normal probability when asked.
16.3 - Using Normal Probabilities to Find X
16.3 - Using Normal Probabilities to Find XOn the last page, we learned how to use the standard normal curve N(0, 1) to find probabilities concerning a normal random variable X with mean \(\mu\) and standard deviation \(\sigma\). What happens if it's not the probability that we want to find, but rather the value of X? That's what we'll investigate on this page. That is, we'll consider what I like to call "inside-out" problems, in which we use known probabilities to find the value of the normal random variable X. Let's start with an example.
Example 16-3
Suppose X, the grade on a midterm exam, is normally distributed with mean 70 and standard deviation 10. The instructor wants to give 15% of the class an A. What cutoff should the instructor use to determine who gets an A?
Solution
My approach to solving this problem is, of course, going to involve drawing a picture:
The instructor now wants to give 10% of the class an A−. What cutoff should the instructor use to determine who gets an A−?
Solution
We'll use the same method as we did previously:
In summary, in order to use a normal probability to find the value of a normal random variable X:
-
Find the z value associated with the normal probability.
-
Use the transformation \(x = \mu + z \sigma\) to find the value of x.
16.4 - Normal Properties
16.4 - Normal PropertiesSo far, all of our attention has been focused on learning how to use the normal distribution to answer some practical problems. We'll turn our attention for a bit to some of the theoretical properties of the normal distribution. We'll start by verifying that the normal p.d.f. is indeed a valid probability distribution. Then, we'll derive the moment-generating function \(M(t)\) of a normal random variable \(X\). We'll conclude by using the moment generating function to prove that the mean and standard deviation of a normal random variable \(X\) are indeed, respectively, \(\mu\) and \(\sigma\), something that we thus far have assumed without proof.
The Normal P.D.F. is Valid
Recall that the probability density function of a normal random variable is:
\(f(x)=\dfrac{1}{\sigma \sqrt{2\pi}} \text{exp}\left\{-\dfrac{1}{2} \left(\dfrac{x-\mu}{\sigma}\right)^2\right\}\)
for \(-\infty<x<\infty\), \(-\infty<\mu<\infty\), and \(0<\sigma<\infty\). Also recall that in order to show that the normal p.d.f. is a valid p.d.f, we need to show that, firstly \(f(x)\) is always positive, and, secondly, if we integrate \(f(x)\) over the entire support, we get 1.
Let's start with the easy part first, namely, showing that \(f(x)\) is always positive. The standard deviation \(\sigma\) is defined to be positive. The square root of \(2\pi\) is positive. And, the natural exponential function is positive. When you multiply positive terms together, you, of course, get a positive number. Check... the first part is done.
Now, for the second part. Showing that \(f(x)\) integrates to 1 is a bit messy, so bear with me here. Let's define \(I\) to be the integral that we are trying to find. That is:
\(I=\int_{-\infty}^\infty \dfrac{1}{\sigma \sqrt{2\pi}} \text{exp}\left\{-\dfrac{1}{2\sigma^2} (x-\mu)^2\right\}dx\)
Our goal is to show that \(I=1\). Now, if we change variables with:
\(w=\dfrac{x-\mu}{\sigma}\)
our integral \(I\) becomes:
\(I=\int_{-\infty}^\infty \dfrac{1}{\sqrt{2\pi}} \text{exp}\left\{-\dfrac{1}{2} w^2\right\}dw\)
Now, squaring both sides, we get:
\(I^2=\left(\int_{-\infty}^\infty \dfrac{1}{\sqrt{2\pi}} \text{exp}\left\{-\dfrac{x^2}{2} \right\}dx\right) \left(\int_{-\infty}^\infty \dfrac{1}{\sqrt{2\pi}} \text{exp}\left\{-\dfrac{y^2}{2} \right\}dy\right)\)
And, pulling the integrals together, we get:
\(I^2=\dfrac{1}{2\pi}\int_{-\infty}^\infty \int_{-\infty}^\infty \text{exp}\left\{-\dfrac{x^2}{2} \right\} \text{exp}\left\{-\dfrac{y^2}{2} \right\}dxdy\)
Now, combining the exponents, we get:
\(I^2=\dfrac{1}{2\pi}\int_{-\infty}^\infty \int_{-\infty}^\infty \text{exp}\left\{-\dfrac{1}{2}(x^2+y^2) \right\} dxdy\)
Converting to polar coordinates with:
\(x=r\cos\theta\) and \(y=r\sin\theta\)
we get:
\(I^2=\dfrac{1}{2\pi}\int_0^{2\pi}\left(\int_0^\infty \text{exp}\left\{-\dfrac{r^2}{2} \right\} rdr\right)d\theta \)
Now, if we do yet another change of variables with:
\(u=\dfrac{r^2}{2}\) and \(du=rdr\)
our integral \(I\) becomes:
\(I^2=\dfrac{1}{2\pi}\int_0^{2\pi}\left(\int_0^\infty e^{-u}du\right)d\theta \)
Evaluating the inside integral, we get:
\(I^2=\dfrac{1}{2\pi}\int_0^{2\pi}\left\{-\lim\limits_{b\to \infty} [e^{-u}]^{u=b}_{u=0}\right\}d\theta \)
And, finally, completing the integration, we get:
\(I^2=\dfrac{1}{2\pi} \int_0^{2\pi} -(0-1) d \theta= \dfrac{1}{2\pi}\int_0^{2\pi} d \theta =\dfrac{1}{2\pi} (2\pi)=1\)
Okay, so we've shown that \(I^2=1\). Therefore, that means that \(I=+1\) or \(I=-1\). But, we know that \(I\) must be positive, since \(f(x)>0\). Therefore, \(I\) must equal 1. Our proof is complete. Finally.
The Moment Generating Function
Theorem
The moment generating function of a normal random variable \(X\) is:
\(M(t)=\text{exp}\left\{\mu t+\dfrac{\sigma^2 t^2}{2}\right\}\)
Proof
Well, I better start this proof out by saying this one is a bit messy, too. Jumping right into it, using the definition of a moment-generating function, we get:
\(M(t)=E(e^{tX})=\int_{-\infty}^\infty e^{tx}f(x)dx=\int_{-\infty}^\infty e^{tx}\left[\dfrac{1}{\sigma \sqrt{2\pi}} \text{exp}\left\{-\dfrac{1}{2\sigma^2} (x-\mu)^2\right\} \right]dx\)
Simply expanding the term in the second exponent, we get:
\(M(t)=\int_{-\infty}^\infty \dfrac{1}{\sigma \sqrt{2\pi}}\text{exp}\{tx\} \text{exp}\left\{-\dfrac{1}{2\sigma^2} (x^2-2x\mu+\mu^2)\right\} dx\)
And, combining the two exponents, we get:
\(M(t)=\int_{-\infty}^\infty \dfrac{1}{\sigma \sqrt{2\pi}} \text{exp}\left\{-\dfrac{1}{2\sigma^2} (x^2-2x\mu+\mu^2)+tx \right\} dx\)
Pulling the \(tx\) term into the parentheses in the exponent, we get:
\(M(t)=\int_{-\infty}^\infty \dfrac{1}{\sigma \sqrt{2\pi}} \text{exp}\left\{-\dfrac{1}{2\sigma^2} (x^2-2x\mu-2\sigma^2tx+\mu^2) \right\} dx\)
And, simplifying just a bit more in the exponent, we get:
\(M(t)=\int_{-\infty}^\infty \dfrac{1}{\sigma \sqrt{2\pi}} \text{exp}\left\{-\dfrac{1}{2\sigma^2} (x^2-2x(\mu+\sigma^2 t)+\mu^2) \right\} dx\)
And, simplifying just a bit more in the exponent, we get:
Now, let's take a little bit of an aside by focusing our attention on just this part of the exponent:
\((x^2-2(\mu+\sigma^2t)x+\mu^2)\)
If we let:
\(a=\mu+\sigma^2t\) and \(b=\mu^2\)
then that part of our exponent becomes:
\(x^2-2(\mu+\sigma^2t)x+\mu^2=x^2-2ax+b\)
Now, complete the square by effectively adding 0:
\(x^2-2(\mu+\sigma^2t)x+\mu^2=x^2-2ax+a^2-a^2+b\)
And, simplifying, we get:
\(x^2-2(\mu+\sigma^2t)x+\mu^2=(x-a)^2-a^2+b\)
Now, inserting in the values we defined for \(a\) and \(b\), we get:
\(x^2-2(\mu+\sigma^2t)x+\mu^2=(x-(\mu+\sigma^2t))^2-(\mu+\sigma^2t)^2+\mu^2\)
Okay, now stick our modified exponent back into where we left off in our calculation of the moment-generating function:
\(M(t)=\int_{-\infty}^\infty \dfrac{1}{\sigma \sqrt{2\pi}}\text{exp}\left\{-\dfrac{1}{2\sigma^2}\left[(x-(\mu+\sigma^2t))^2-(\mu+\sigma^2t)^2+\mu^2\right]\right\}dx\)
We can now pull the part of the exponent that doesn't depend on \(x\) through the integral getting:
\(M(t)=\text{exp}\left\{-\dfrac{1}{2\sigma^2}\left[-(\mu+\sigma^2t)^2+\mu^2\right]\right\} \int_{-\infty}^\infty \dfrac{1}{\sigma \sqrt{2\pi}}\text{exp}\left\{-\dfrac{1}{2\sigma^2}\left[(x-(\mu+\sigma^2t))^2 \right]\right\}dx\)
Now, we should recognize that the integral integrates to 1 because it is the integral over the entire support of the p.d.f. of a normal random variable \(X\) with:
mean \(\mu+\sigma^2t\) and variance \(\sigma^2\)
That is, because the integral is 1:
\(\int_{-\infty}^\infty \dfrac{1}{\sigma \sqrt{2\pi}}\text{exp}\left\{-\dfrac{1}{2\sigma^2}\left[(x-(\mu+\sigma^2t))^2 \right]\right\}dx = 1\)
\(\text{Since, }\ N(\mu+\sigma^2t, \sigma^2)\)
our moment-generating function reduces to this:
\(M(t)=\text{exp}\left\{-\dfrac{1}{2\sigma^2}\left[-\mu^2-2\mu\sigma^2t-\sigma^4t^2+\mu^2\right]\right\}\)
Now, it's just a matter of simplifying:
\(M(t)=\text{exp}\left\{\dfrac{2\mu\sigma^2t+\sigma^4t^2}{2\sigma^2}\right\}\)
and simplifying a bit more:
\(M(t)=\text{exp}\left\{\mu t +\dfrac{\sigma^2t^2}{2}\right\}\)
Our second messy proof is complete!
The Mean and Variance
Theorem
The mean and variance of a normal random variable \(X\) are, respectively, \(\mu\) and \(\sigma^2\).
Proof
We'll use the moment generating function:
\(M(t)=\text{exp}\left\{\mu t +\dfrac{\sigma^2t^2}{2}\right\}\)
to find the mean and variance. Recall that finding the mean involves evaluating the derivative of the moment-generating function with respect to \(t\) at \(t=0\):
So, we just found that the first derivative of the moment-generating function with respect to \(t\) is:
\(M'(t)=\text{exp}\left(\mu t +\dfrac{\sigma^2t^2}{2}\right)\times (\mu+\sigma^2t)\)
We'll use it to help us find the variance:
16.5 - The Standard Normal and The Chi-Square
16.5 - The Standard Normal and The Chi-SquareTheorem
We have one more theoretical topic to address before getting back to some practical applications on the next page, and that is the relationship between the normal distribution and the chi-square distribution. The following theorem clarifies the relationship.
If \(X\) is normally distributed with mean \(\mu\) and variance \(\sigma^2>0\), then:
\(V=\left(\dfrac{X-\mu}{\sigma}\right)^2=Z^2\)
is distributed as a chi-square random variable with 1 degree of freedom.
Proof
To prove this theorem, we need to show that the p.d.f. of the random variable \(V\) is the same as the p.d.f. of a chi-square random variable with 1 degree of freedom. That is, we need to show that:
\(g(v)=\dfrac{1}{\Gamma(1/2)2^{1/2}}v^{\frac{1}{2}-1} e^{-v/2}\)
The strategy we'll take is to find \(G(v)\), the cumulative distribution function of \(V\), and then differentiate it to get \(g(v)\), the probability density function of \(V\). That said, we start with the definition of the cumulative distribution function of \(V\):
\(G(v)=P(V\leq v)=P(Z^2 \leq v)\)
That second equality comes, of course, from the fact that \(V=Z^2\). Now, taking note of the behavior of a parabolic function:
we can simplify \(G(v)\) to get:
\(G(v)=P(-\sqrt{v} < Z <\sqrt{v})\)
Now, to find the desired probability we need to integrate, over the given interval, the probability density function of a standard normal random variable \(Z\). That is:
\(G(v)= \int^{\sqrt{v}}_{-\sqrt{v}}\dfrac{1}{ \sqrt{2\pi}}\text{exp} \left(-\dfrac{z^2}{2}\right) dz\)
By the symmetry of the normal distribution, we can integrate over just the positive portion of the integral, and then multiply by two:
\(G(v)= 2\int^{\sqrt{v}}_0 \dfrac{1}{ \sqrt{2\pi}}\text{exp} \left(-\dfrac{z^2}{2}\right) dz\)
Okay, now let's do the following change of variables:
\(\text{Let}\ z=\sqrt{y}=y^{1/2}\)
\(\text{So, }\ dz=\frac{1}{2}y^{-1/2}\ dy=\frac{1}{z\sqrt{y}}dy\)
\(z^2=y,\ \\ \begin{aligned} z&=0 \Rightarrow y=0 \\ z&=\sqrt{v} \Rightarrow y=v\end{aligned}\)
Doing so, we get:
\(G(v)= 2\int^v_0 \dfrac{1}{ \sqrt{2\pi}}\text{exp} \left(-\dfrac{y}{2}\right) \left(\dfrac{1}{2\sqrt{y}}\right) dy\)
\(G(v)= \int^v_0 \dfrac{1}{ \sqrt{\pi}\sqrt{2}} y^{\frac{1}{2}-1} \text{exp} \left(-\dfrac{y}{2}\right) dy\)
for \(v>0\). Now, by one form of the Fundamental Theorem of Calculus:
\(\text{Given, }\)
\(\int^x_a f(t)dt=F(x)-F(a)\)
\(\frac{d}{dx}\int^x_a f(t)dt=F'(x)=f(x)\)
we can take the derivative of \(G(v)\) to get the probability density function \(g(v)\):
\(g(v)=G'(v)= \dfrac{1}{ \sqrt{\pi}\sqrt{2}} v^{\frac{1}{2}-1} e^{-v/2}\)
for \(0<v<\infty\). If you compare this \(g(v)\) to the first \(g(v)\) that we said we needed to find way back at the beginning of this proof, you should see that we are done if the following is true:
\(\Gamma \left(\dfrac{1}{2}\right)=\sqrt{\pi}\)
It is indeed true, as the following argument illustrates. Because \(g(v)\) is a p.d.f., the integral of the p.d.f. over the support must equal 1:
\(\int_0^\infty \dfrac{1}{ \sqrt{\pi}\sqrt{2}} v^{\frac{1}{2}-1} e^{-v/2} dv=1\)
Now, change the variables by letting \(v=2x\), so that \(dv=2dx\). Making the change, we get:
\(\dfrac{1}{ \sqrt{\pi}} \int_0^\infty \dfrac{1}{ \sqrt{2}} (2x)^{\frac{1}{2}-1} e^{-x}2dx=1\)
Rewriting things just a bit, we get:
\(\dfrac{1}{ \sqrt{\pi}} \int_0^\infty \dfrac{1}{ \sqrt{2}}\dfrac{1}{ \sqrt{2}} x^{\frac{1}{2}-1} e^{-x}2dx=1\)
And simplifying, we get:
\(\dfrac{1}{ \sqrt{\pi}} \int_0^\infty x^{\frac{1}{2}-1} e^{-x} dx=1\)
Now, it's just a matter of recognizing that the integral is the gamma function of \(\frac{1}{2}\):
\(\dfrac{1}{ \sqrt{\pi}} \Gamma \left(\dfrac{1}{2}\right)=1\)
Our proof is complete.
So, now that we've taken care of the theoretical argument. Let's take a look at an example to see that the theorem is, in fact, believable in a practical sense.
Example 16-4
Find the probability that the standard normal random variable \(Z\) falls between −1.96 and 1.96 in two ways:
- using the standard normal distribution
- using the chi-square distribution
Solution
The standard normal table (Table V in the textbook) yields:
\(P(-1.96<Z<1.96)=P(Z<1.96)-P(Z>1.96)=0.975-0.025=0.95\)
The chi-square table (Table IV in the textbook) yields the same answer:
\(P(-1.96<Z<1.96)=P(|Z|<1.96)=P(Z^2<1.96^2)=P(\chi^2_{(1)})<3.8416)=0.95\)
16.6 - Some Applications
16.6 - Some ApplicationsInterpretation of Z
Note that the transformation from \(X\) to \(Z\):
\(Z=\dfrac{X-\mu}{\sigma}\)
tells us the number of standard deviations above or below the mean that \(X\) falls. That is, if \(Z=-2\), then we know that \(X\) falls 2 standard deviations below the mean. And if \(Z=+2\), then we know that \(X\) falls 2 standard deviations above the mean. As such, \(Z\)-scores are sometimes used in medical fields to identify whether an individual exhibits extreme values with respect to some biological or physical measurement.
Example 16-5
Post-menopausal women are known to be susceptible to severe bone loss known as osteoporosis. In some cases, bone loss can be so extreme as to cause a woman to lose a few inches of height. The spines and hips of women who are suspected of having osteoporosis are therefore routinely scanned to ensure that their bone loss hasn't become so severe to warrant medical intervention.
The mean \(\mu\) and standard deviation \(\sigma\) of the density of the bones in the spine, for example, are known for a healthy population. A woman is scanned and \(x\), the bone density of her spine is determined. She and her doctor would then naturally want to know whether the woman's bone density \(x\) is extreme enough to warrant medical intervention. The most common way of evaluating whether a particular \(x\) is extreme is to use the mean \(\mu\), the standard deviation \(\sigma\), and the value \(x\) to calculate a \(Z\)-score. The \(Z\)-score can then be converted to a percentile to provide the doctor and the woman an indication of the severity of her bone loss.
Suppose the woman's \(Z\)-score is −2.36, for example. The doctor then knows that the woman's bone density falls 2.36 standard deviations below the average bone density of a healthy population. The doctor, furthermore, knows that fewer than 1% of the population have a bone density more extreme than that of his/her patient.
The Empirical Rule Revisited
You might recall earlier in this section, when we investigated exploring continuous data, that we learned about the Empirical Rule. Specifically, we learned that if a histogram is at least approximately bell-shaped, then:
- approximately 68% of the data fall within one standard deviation of the mean
- approximately 95% of the data fall within two standard deviations of the mean
- approximately 99.7% of the data fall within three standard deviations of the mean
Where did those numbers come from? Now, that we've got the normal distribution under our belt, we can see why the Empirical Rule holds true. The probability that a randomly selected data value from a normal distribution falls within one standard deviation of the mean is
\(P(-1<Z<1)=P(Z<1)-P(Z>1)=0.8413-0.1587=0.6826\)
That is, we should expect 68.26% (approximately 68%!) of the data values arising from a normal population to be within one standard deviation of the mean, that is, to fall in the interval:
\((\mu-\sigma, \mu+\sigma)\)
The probability that a randomly selected data value from a normal distribution falls within two standard deviations of the mean is
\(P(-2<Z<2)=P(Z<2)-P(Z>2)=0.9772-0.0228=0.9544\)
That is, we should expect 95.44% (approximately 95%!) of the data values arising from a normal population to be within two standard deviations of the mean, that is, to fall in the interval:
\((\mu-2\sigma, \mu+2\sigma)\)
And, the probability that a randomly selected data value from a normal distribution falls within three standard deviations of the mean is:
\(P(-3<Z<3)=P(Z<3)-P(Z>3)=0.9987-0.0013=0.9974\)
That is, we should expect 99.74% (almost all!) of the data values arising from a normal population to be within three standard deviations of the mean, that is, to fall in the interval:
\((\mu-3\sigma, \mu+3\sigma)\)
Let's take a look at an example of the Empirical Rule in action.
Example 16-6
The left arm length, in inches, of 213 students were measured. Here's the resulting data, and a picture of a dot plot of the resulting arm lengths:
As you can see, the plot suggests that the distribution of the data is at least bell-shaped enough to warrant the assumption that \(X\), the left arm lengths of students, is normally distributed. We can use the raw data to determine that the average arm length of the 213 students measured is 25.167 inches, while the standard deviation is 2.095 inches. We'll then use 25.167 as an estimate of \(\mu\), the average left arm length of all college students, and 2.095 as an estimate of \(\sigma\), the standard deviation of the left arm lengths of all college students.
The Empirical Rule tells us then that we should expect approximately 68% of all college students to have a left arm length between:
\(\bar{x}-s=25.167-2.095=23.072\) and \(\bar{x}+s=25.167+2.095=27.262\)
inches. We should also expect approximately 95% of all college students to have a left arm length between:
\(\bar{x}-2s=25.167-2(2.095)=20.977\) and \(\bar{x}+2s=25.167+2(2.095)=29.357\)
inches. And, we should also expect approximately 99.7% of all college students to have a left arm length between:
\(\bar{x}-3s=25.167-3(2.095)=18.882\) and \(\bar{x}+3s=25.167+3(2.095)=31.452\)
Let's see what percentage of our 213 arm lengths fall in each of these intervals! It takes some work if you try to do it by hand, but statistical software can quickly determine that:
- 143, or 67.14%, of the 213 arm lengths fall in the first interval
- 204, or 95.77%, of the 213 arm lengths fall in the second interval
- 213, or 100%, of the 213 arm lengths fall in the third interval
The Empirical Rule didn't do too badly, eh?