Lesson 17: Distributions of Two Discrete Random Variables

Overview

As the title of the lesson suggests, in this lesson, we'll learn how to extend the concept of a probability distribution of one random variable \(X\) to a joint probability distribution of two random variables \(X\) and \(Y\). In some cases, \(X\) and \(Y\)may both be discrete random variables. For example, suppose \(X\) denotes the number of significant others a randomly selected person has, and \(Y\) denotes the number of arguments the person has each week. We might want to know if there is a relationship between \(X\) and \(Y\). Or, we might want to know the probability that \(X\) takes on a particular value \(x\) and \(Y\) takes on a particular value \(y\). That is, we might want to know \(P(X=x, Y=y)\).

Objectives

Upon completion of this lesson, you should be able to:

To learn the formal definition of a joint probability mass function of two discrete random variables.
To learn how to use a joint probability mass function to find the probability of a specific event.
To learn how to find a marginal probability mass function of a discrete random variable \(X\) from the joint probability mass function of \(X\) and \(Y\).
To learn a formal definition of the independence of two random variables \(X\) and \(Y\).
To learn how to find the expectation of a function of the discrete random variables \(X\) and \(Y\) using their joint probability mass function.
To learn how to find the means and variances of the discrete random variables \(X\) and \(Y\) using their joint probability mass function.
To learn what it means that \(X\) and \(Y\) have a joint triangular support.
To learn that, in general, any two random variables \(X\) and \(Y\) having a joint triangular support must be dependent.
To learn what it means that \(X\) and \(Y\) have a joint rectangular support.
To learn that, in general, any two random variables \(X\) and \(Y\) having a joint rectangular support may or may not be independent.
To learn about the trinomial distribution.
To be able to apply the methods learned in the lesson to new problems.

17.1 - Two Discrete Random Variables

Let's start by first considering the case in which the two random variables under consideration, \(X\) and \(Y\), say, are both discrete. We'll jump in right in and start with an example, from which we will merely extend many of the definitions we've learned for one discrete random variable, such as the probability mass function, mean and variance, to the case in which we have two discrete random variables.

Example 17-1

Suppose we toss a pair of fair, four-sided dice, in which one of the dice is RED and the other is BLACK. We'll let:

\(X\) = the outcome on the RED die = \(\{1, 2, 3, 4\}\)
\(Y\) = the outcome on the BLACK die = \(\{1, 2, 3, 4\}\)

What is the probability that \(X\) takes on a particular value \(x\), and \(Y\) takes on a particular value \(y\)? That is, what is \(P(X=x, Y=y)\)?

Solution

Just as we have to in the case with one discrete random variable, in order to find the "joint probability distribution" of \(X\) and \(Y\), we first need to define the support of \(X\) and \(Y\). Well, the support of \(X\) is:

\(S_1=\{1, 2, 3, 4\}\)

And, the support of \(Y\) is:

\(S_2=\{1, 2, 3, 4\}\)

Now, if we let \((x,y)\) denote one of the possible outcomes of one toss of the pair of dice, then certainly (1, 1) is a possible outcome, as is (1, 2), (1, 3) and (1, 4). If we continue to enumerate all of the possible outcomes, we soon see that the joint support S has 16 possible outcomes:

\(S=\{(1,1), (1,2), (1,3), (1,4), (2,1), (2,2), (2,3), (2,4), (3,1), (3,2), (3,3), (3,4), (4,1), (4,2), (4,3), (4,4)\}\)

Now, because the dice are fair, we should expect each of the 16 possible outcomes to be equally likely. Therefore, using the classical approach to assigning probability, the probability that \(X\) equals any particular \(x\) value, and \(Y\) equals any particular \(y\) value, is \(\frac{1}{16}\). That is, for all \((x,y)\) in the support \(S\):

\(P(X=x, Y=y)=\frac{1}{16}\)

Because we have identified the probability for each \((x, y)\), we have found what we call the joint probability mass function. Perhaps, it is not too surprising that the joint probability mass function, which is typically denoted as \(f(x,y)\), can be defined as a formula (as we have above), as a graph, or as a table. Here's what our joint p.m.f. would like in tabular form:

Now that we've found our first joint probability mass function, let's formally define it now.

Joint Probability Mass Function: Let \(X\) and \(Y\) be two discrete random variables, and let \(S\) denote the two-dimensional support of \(X\) and \(Y\). Then, the function \(f(x,y)=P(X=x, Y=y)\) is a joint probability mass function (abbreviated p.m.f.) if it satisfies the following three conditions:

\(0 \leq f(x,y) \leq 1\)
\(\mathop{\sum\sum}\limits_{(x,y)\in S} f(x,y)=1\)
\(P[(X,Y) \in A]=\mathop{\sum\sum}\limits_{(x,y)\in A} f(x,y)\) where \(A\) is a subset of the support \(S\).

The first condition, of course, just tells us that each probability must be a valid probability number between 0 and 1 (inclusive). The second condition tells us that, just as must be true for a p.m.f. of one discrete random variable, the sum of the probabilities over the entire support \(S\) must equal 1. The third condition tells us that in order to determine the probability of an event \(A\), you simply sum up the probabilities of the \((x,y)\) values in \(A\).

Now, if you take a look back at the representation of our joint p.m.f. in tabular form, you can see that the last column contains the probability mass function of \(X\) alone, and the last row contains the probability mass function of \(Y\) alone. Those two functions, \(f(x)\) and \(f(y)\), which in this setting are typically referred to as marginal probability mass functions, are obtained by simply summing the probabilities over the support of the other variable. That is, to find the probability mass function of \(X\), we sum, for each \(x\), the probabilities when \(y=1, 2, 3, \text{ and } 4\). That is, for each \(x\), we sum \(f(x, 1), f(x, 2), f(x, 3), \text{ and }f(x, 4)\). Now that we've seen the two marginal probability mass functions in our example, let's give a formal definition of a marginal probability mass function.

Marginal Probability Mass Function of \(X\)

Let \(X\) be a discrete random variable with support \(S_1\), and let \(Y\) be a discrete random variable with support \(S_2\). Let \(X\) and \(Y\) have the joint probability mass function \(f(x, y)\) with support \(S\). Then, the probability mass function of \(X\) alone, which is called the marginal probability mass function of \(X\), is defined by:

\(f_X(x)=\sum\limits_y f(x,y)=P(X=x),\qquad x\in S_1\)

where, for each \(x\) in the support \(S_1\), the summation is taken over all possible values of \(y\). Similarly, the probability mass function of \(Y\) alone, which is called the marginal probability mass function of \(Y\), is defined by:

\(f_Y(y)=\sum\limits_x f(x,y)=P(Y=y),\qquad y\in S_2\)

where, for each \(y\) in the support \(S_2\), the summation is taken over all possible values of \(x\).

If you again take a look back at the representation of our joint p.m.f. in tabular form, you might notice that the following holds true:

\(P(X=x,Y=y)=\dfrac{1}{16}=P(X=x)\cdot P(Y=y)=\dfrac{1}{4} \cdot \dfrac{1}{4}=\dfrac{1}{16}\)

for all \(x\in S_1, y\in S_2\). When this happens, we say that \(X\) and \(Y\) are independent. A formal definition of the independence of two random variables \(X\) and \(Y\) follows.

Independent and Dependent Random Variables

The random variables \(X\) and \(Y\) are independent if and only if:

\(P(X=x, Y=y)=P(X=x)\times P(Y=y)\)

for all \(x\in S_1, y\in S_2\). Otherwise, \(X\) and \(Y\) are said to be dependent.

Now, suppose we were given a joint probability mass function \(f(x, y)\), and we wanted to find the mean of \(X\). Well, one strategy would be to find the marginal p.m.f of \(X\) first, and then use the definition of the expected value that we previously learned to calculate \(E(X)\). Alternatively, we could use the following definition of the mean that has been extended to accommodate joint probability mass functions.

Definition. Let \(X\) be a discrete random variable with support \(S_1\), and let \(Y\) be a discrete random variable with support \(S_2\). Let \(X\) and \(Y\) be discrete random variables with joint p.m.f. \(f(x,y)\) on the support \(S\). If \(u(X,Y)\) is a function of these two random variables, then:

\(E[u(X,Y)]=\mathop{\sum\sum}\limits_{(x,y)\in S} u(x,y)f(x,y)\)

if it exists, is called the expected value of \(u(X,Y)\). If \(u(X,Y)=X\), then:

\(\mu_X=E[X]=\sum\limits_{x\in S_1} \sum\limits_{y\in S_2} xf(x,y)\)

if it exists, is the mean of \(X\). If \(u(X,Y)=Y\), then:

\(\mu_Y=E[Y]=\sum\limits_{x\in S_1} \sum\limits_{y\in S_2} yf(x,y)\)

if it exists, is the mean of \(Y\).

Example 17-1 (continued)

Consider again our example in which we toss a pair of fair, four-sided dice, in which one of the dice is RED and the other is BLACK. Again, letting:

\(X\) = the outcome on the RED die = \(\{1, 2, 3, 4\}\)
\(Y\) = the outcome on the BLACK die = \(\{1, 2, 3, 4\}\)

What is the mean of \(X\) ? And, what is the mean of \(Y\)?

Solution

The mean of \(X\) is calculated as:

\(\mu_X=E[X]=\sum\limits_{x\in S_1} \sum\limits_{y\in S_2} xf(x,y) =1\left(\dfrac{1}{16}\right)+\cdots+1\left(\dfrac{1}{16}\right)+\cdots+4\left(\dfrac{1}{16}\right)+\cdots+4\left(\dfrac{1}{16}\right)\)

which simplifies to:

\(\mu_X=E[X]=1\left(\dfrac{4}{16}\right)+2\left(\dfrac{4}{16}\right)+3\left(\dfrac{4}{16}\right)+4\left(\dfrac{4}{16}\right)=\dfrac{40}{16}=2.5\)

The mean of \(Y\) is similarly calculated as:

\(\mu_Y=E[Y]=\sum\limits_{x\in S_1} \sum\limits_{y\in S_2} yf(x,y)=1\left(\dfrac{1}{16}\right)+\cdots+1\left(\dfrac{1}{16}\right)+\cdots+4\left(\dfrac{1}{16}\right)+\cdots+4\left(\dfrac{1}{16}\right)\)

which simplifies to:

\(\mu_Y=E[Y]=1\left(\dfrac{4}{16}\right)+2\left(\dfrac{4}{16}\right)+3\left(\dfrac{4}{16}\right)+4\left(\dfrac{4}{16}\right)=\dfrac{40}{16}=2.5\)

By the way, you probably shouldn't find it surprising that the formula for the mean of \(X\) reduces to:

\(\mu_X=\sum\limits_{x\in S_1} xf(x)\)

because:

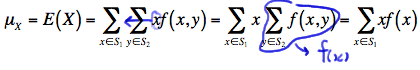
Why mean of X reduces

That is, the third equality holds because the x values don't depend on \(y\) and therefore can be pulled through the summation over \(y\). And, the last equality holds because of the definition of the marginal probability mass function of \(X\). Similarly, the mean of \(Y\) reduces to:

\(\mu_Y=\sum\limits_{y\in S_2} yf(y)\)

because:

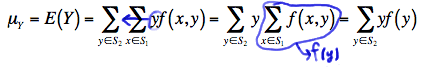
Why Mean of Y reduces

That is, again, the third equality holds because the y values don't depend on \(x\) and therefore can be pulled through the summation over \(x\). And, the last equality holds because of the definition of the marginal probability mass function of \(Y\).

Now, suppose we were given a joint probability mass function \(f(x,y)\), and we wanted to find the variance of \(X\). Again, one strategy would be to find the marginal p.m.f of \(X\) first, and then use the definition of the expected value that we previously learned to calculate \(\text{Var}(X)\). Alternatively, we could use the following definition of the variance that has been extended to accommodate joint probability mass functions.

Definition. Let \(X\) be a discrete random variable with support \(S_1\), and let \(Y\) be a discrete random variable with support \(S_2\). Let \(X\) and \(Y\) be discrete random variables with joint p.m.f. \(f(x,y)\) on the support \(S\). If \(u(X,Y)\) is a function of these two random variables, then:

\(E[u(X,Y)]=\mathop{\sum\sum}\limits_{(x,y)\in S} u(x,y)f(x,y)\)

if it exists, is called the expected value of \(u(X,Y)\). If \(u(X,Y)=(X-\mu_X)^2\), then:

\(\sigma^2_X=Var[X]=\sum\limits_{x\in S_1} \sum\limits_{y\in S_2} (x-\mu_X)^2 f(x,y)\)

if it exists, is the variance of \(X\). The variance of \(X\) can also be calculated using the shortcut formula:

\(\sigma^2_X=E(X^2)-\mu^2_X=\left(\sum\limits_{x\in S_1} \sum\limits_{y\in S_2} x^2 f(x,y)\right)-\mu^2_X\)

If \(u(X,Y)=(Y-\mu_Y)^2\), then:

\(\sigma^2_Y=Var[Y]=\sum\limits_{x\in S_1} \sum\limits_{y\in S_2} (y-\mu_Y)^2 f(x,y)\)

if it exists, is the variance of \(Y\). The variance of \(Y\) can also be calculated using the shortcut formula:

\(\sigma^2_Y=E(Y^2)-\mu^2_Y=\left(\sum\limits_{x\in S_1} \sum\limits_{y\in S_2} y^2 f(x,y)\right)-\mu^2_Y\)

Example 17-1 (continued again)

Consider yet again our example in which we toss a pair of fair, four-sided dice, in which one of the dice is RED and the other is BLACK. Again, letting:

\(X\) = the outcome on the RED die = \(\{1, 2, 3, 4\}\)
\(Y\) = the outcome on the BLACK die = \(\{1, 2, 3, 4\}\)

What is the variance of \(X\) ? And, what is the variance of \(Y\)?

Solution

Using the definition, the variance of \(X\) is calculated as:

\(\sigma^2_X=\sum\limits_{x\in S_1} \sum\limits_{y\in S_2} (x-\mu_X)^2 f(x,y)=(1-2.5)^2\left(\dfrac{1}{16}\right)+\cdots+(4-2.5)^2\left(\dfrac{1}{16}\right)=1.25\)

Thankfully, we get the same answer using the shortcut formula for the variance of \(X\):

\(\sigma^2_X=E(X^2)-\mu^2_X=\left(\sum\limits_{x\in S_1} \sum\limits_{y\in S_2} x^2 f(x,y)\right)-\mu^2_X=\left[1^2 \left(\dfrac{1}{16}\right)+\cdots+4^2 \left(\dfrac{1}{16}\right)\right]-2.5^2=\dfrac{120}{16}-6.25=1.25\)

Calculating the variance of \(Y\) is left for you as an exercise. You should, because of the symmetry, also get \(\text{Var}(Y)=1.25\).

17.2 - A Triangular Support

We now have many of the gory definitions behind us. One of the definitions we learned in particular is that two random variables \(X\) and \(Y\) are independent if and only if:

\(P(X=x, Y=x)=P(X=x)\times P(Y=y)\)

for all \(x\in S_1, y\in S_2\). Otherwise, \(X\) and \(Y\) are said to be dependent. On the previous page, our example comprised two random variables \(X\) and \(Y\), which were deemed to be independent. On this page, we'll explore, by way of another example, two random variables \(X\) and \(Y\), which are deemed to be dependent.

Example 17-2

Consider the following joint probability mass function:

\(f(x,y)=\dfrac{xy^2}{13}\)

in which the support is \(S=\{(x, y)\}=\{(1, 1), (1, 2), (2,2)\}\). Are the random variables \(X\) and \(Y\) independent?

Solution

We are given the joint probability mass function as a formula. We can therefore easily calculate the joint probabilities for each \((x, y)\) in the support \(S\):

when \(x=1\) and \(y=1\): \(f(1,1)=\dfrac{(1)(1)^2}{13}=\dfrac{1}{13}\)

when \(x=1\) and \(y=2\): \(f(1,2)=\dfrac{(1)(2)^2}{13}=\dfrac{4}{13}\)

when \(x=2\) and \(y=2\): \(f(2,2)=\dfrac{(2)(2)^2}{13}=\dfrac{8}{13}\)

Now that we have calculated each of the joint probabilities, we can alternatively present the p.m.f. in tabular form, complete with the marginal p.m.f.s of \(X\) and \(Y\), as:

As an aside, you should note that the joint support \(S\) of \(X\) and \(Y\) is what we call a "triangular support," because, well, it's shaped like a triangle:

Anyway, perhaps it is easy now to see that \(X\) and \(Y\) are dependent, because, for example:

\(f(1,2)=\dfrac{4}{13} \neq f_X(1)\cdot f_Y(2)=\dfrac{5}{13} \times \dfrac{12}{13}\)

Note though that, in general, any two random variables \(X\) and \(Y\) having a joint triangular support must be dependent because you can always find:

\(f(x)\times f(y)=c\ne0\)

for some non-zero constant \(c\). For example, for the joint p.m.f. above:

\(f_X(2)\times f_Y(1)=\left(\frac{8}{13}\right)\times\left(\frac{1}{13}\right)=\frac{8}{169}\ne 0=f_{X,Y}(2,1)\)

In general, random variables with rectangular support may or may not be independent.

17.3 - The Trinomial Distribution

You might recall that the binomial distribution describes the behavior of a discrete random variable \(X\), where \(X\) is the number of successes in \(n\) tries when each try results in one of only two possible outcomes. What happens if there aren't two, but rather three, possible outcomes? That's what we'll explore here on this page, ending up not with the binomial distribution, but rather the trinomial distribution. A rather fitting name, I might say!

Example 17-3

Suppose \(n=20\) students are selected at random:

Let \(A\) be the event that a randomly selected student went to the football game on Saturday. Also, let \(P(A)=0.20=p_1\), say.
Let \(B\) be the event that a randomly selected student watched the football game on TV on Saturday. Let \(P(B)=0.50=p_2\), say.
Let \(C\) be the event that a randomly selected student completely ignored the football game on Saturday. Let \(P(C)=0.3=1-p_1-p_2\).

One possible outcome, then, of selecting the 20 students at random is:

BBCABBAACABBBCCBCBCB

That is, the first two students watched the game on TV, the third student ignored the game, the fourth student went to the game, and so on. Now, if we let \(X\)denote the number in the sample who went to the football game on Saturday, let \(Y\) denote the number in the sample who watched the football game on TV on Saturday, and let \(Z\) denote the number in the sample who completely ignored the football game, then in this case:

\(X=4\) (because there are 4 As)
\(Y=10\) (because there are 10 Bs)
\(Z=20-X-Y\) (and yes, indeed, there are 6 Cs)

What is the joint probability mass function of \(X\)and \(Y\)?

Solution

This example lends itself to the following formal definition.

Definition. Suppose we repeat an experiment \(n\) independent times, with each experiment ending in one of three mutually exclusive and exhaustive ways (success, first kind of failure, second kind of failure). If we let \(X\) denote the number of times the experiment results in a success, let \(Y\) denote the number of times the experiment results in a failure of the first kind, and let \(Z\) denote the number of times the experiment results in a failure of the second kind, then the joint probability mass function of \(X\) and \(Y\) is:

\(f(x,y)=P(X=x,Y=y)=\dfrac{n!}{x!y!(n-x-y)!} p^x_1 p^y_2 (1-p_1-p_2)^{n-x-y}\)

with:

\(x=0, 1, \ldots, n\)

\(y=0, 1, \ldots, n\)

\(x+y\le n\)

Example 17-3 continued

What are the marginal probability mass functions of \(X\)and \(Y\)? Are \(X\)and \(Y\) independent? or dependent?

Solution

We can easily just lump the two kinds of failures back together, thereby getting that \(X\), the number of successes, is a binomial random variable with parameters \(n\) and \(p_1\). That is:

\(f(x)=\dfrac{n!}{x!(n-x)!} p^x_1 (1-p_1)^{n-x}\)

with \(x=0, 1, \ldots, n\). Similarly, we can lump the successes in with the failures of the second kind, thereby getting that \(Y\), the number of failures of the first kind, is a binomial random variable with parameters \(n\) and \(p_2\). That is:

\(f(y)=\dfrac{n!}{y!(n-y)!} p^y_2 (1-p_2)^{n-y}\)

with \(y=0, 1, \ldots, n\). Therefore, \(X\) and \(Y\) must be dependent, because if we multiply the p.m.f.s of \(X\) and \(Y\) together, we don't get the trinomial p.m.f. That is, \(f(x,y)\ne f(x)\times f(y)\):

\(\left[\dfrac{n!}{x!y!(n-x-y)!} p^x_1 p^y_2 (1-p_1-p_2)^{n-x-y}\right] \neq \left[\dfrac{n!}{x!(n-x)!} p^x_1 (1-p_1)^{n-x}\right] \times \left[\dfrac{n!}{y!(n-y)!} p^y_2 (1-p_2)^{n-y}\right]\)

By the way, there's also another way of arguing that \(X\) and \(Y\) must be dependent... because the joint support of \(X\) and \(Y\) is triangular!

Lesson 18: The Correlation Coefficient

Overview

In the previous lesson, we learned about the joint probability distribution of two random variables \(X\) and \(Y\). In this lesson, we'll extend our investigation of the relationship between two random variables by learning how to quantify the extent or degree to which two random variables \(X\) and \(Y\) are associated or correlated. For example, Suppose \(X\) denotes the number of cups of hot chocolate sold daily at a local café, and \(Y\) denotes the number of apple cinnamon muffins sold daily at the same café. Then, the manager of the café might benefit from knowing whether \(X\) and \(Y\) are highly correlated or not. If the random variables are highly correlated, then the manager would know to make sure that both are available on a given day. If the random variables are not highly correlated, then the manager would know that it would be okay to have one of the items available without the other. As the title of the lesson suggests, the correlation coefficient is the statistical measure that is going to allow us to quantify the degree of correlation between two random variables \(X\) and \(Y\).

To learn a formal definition of the covariance between two random variables \(X\) and \(Y\).
To learn how to calculate the covariance between any two random variables \(X\) and \(Y\).
To learn a shortcut, or alternative, formula for the covariance between two random variables \(X\) and \(Y\).
To learn a formal definition of the correlation coefficient between two random variables \(X\) and \(Y\).
To learn how to calculate the correlation coefficient between any two random variables \(X\) and \(Y\).
To learn how to interpret the correlation coefficient between any two random variables \(X\) and \(Y\).
To learn that if \(X\) and \(Y\) are independent random variables, then the covariance and correlation between \(X\) and \(Y\) are both zero.
To learn that if the correlation between \(X\) and \(Y\) is 0, then\(X\) and \(Y\) are not necessarily independent.
To learn how the correlation coefficient gets its sign.
To learn that the correlation coefficient measures the strength of the linear relationship between two random variables \(X\) and \(Y\).
To learn that the correlation coefficient is necessarily a number between −1 and +1.
To understand the steps involved in each of the proofs in the lesson.
To be able to apply the methods learned in the lesson to new problems.

18.1 - Covariance of X and Y

Here, we'll begin our attempt to quantify the dependence between two random variables \(X\) and \(Y\) by investigating what is called the covariance between the two random variables. We'll jump right in with a formal definition of the covariance.

Covariance

Let \(X\) and \(Y\) be random variables (discrete or continuous!) with means \(\mu_X\) and \(\mu_Y\). The covariance of \(X\) and \(Y\), denoted \(\text{Cov}(X,Y)\) or \(\sigma_{XY}\), is defined as:

\(Cov(X,Y)=\sigma_{XY}=E[(X-\mu_X)(Y-\mu_Y)]\)

That is, if \(X\) and \(Y\) are discrete random variables with joint support \(S\), then the covariance of \(X\) and \(Y\) is:

\(Cov(X,Y)=\mathop{\sum\sum}\limits_{(x,y)\in S} (x-\mu_X)(y-\mu_Y) f(x,y)\)

And, if \(X\) and \(Y\) are continuous random variables with supports \(S_1\) and \(S_2\), respectively, then the covariance of \(X\) and \(Y\) is:

\(Cov(X,Y)=\int_{S_2} \int_{S_1} (x-\mu_X)(y-\mu_Y) f(x,y)dxdy\)

Example 18-1

Suppose that \(X\) and \(Y\) have the following joint probability mass function:

\( \begin{array}{cc|ccc|c} & f(x, y) & 1 & 2 & 3 & f_{X}(x) \\ \hline x & 1 & 0.25 & 0.25 & 0 & 0.5 \\ & 2 & 0 & 0.25 & 0.25 & 0.5 \\ \hline & f_{Y}(y) & 0.25 & 0.5 & 0.25 & 1 \end{array} \)

so that \(\mu_{\mathrm{x}}=3 / 2\), \(\mu_{\mathrm{Y}}=2, \sigma_{\mathrm{X}}=1 / 2\), and \(\sigma_{\mathrm{Y}}=\sqrt{1/2}\)

What is the covariance of \(X\) and \(Y\)?

Solution

Two questions you might have right now: 1) What does the covariance mean? That is, what does it tell us? and 2) Is there a shortcut formula for the covariance just as there is for the variance? We'll be answering the first question in the pages that follow. Well, sort of! In reality, we'll use the covariance as a stepping stone to yet another statistical measure known as the correlation coefficient. And, we'll certainly spend some time learning what the correlation coefficient tells us. In regards to the second question, let's answer that one now by way of the following theorem.

Theorem

For any random variables \(X\) and \(Y\) (discrete or continuous!) with means \(\mu_X\) and \(\mu_Y\), the covariance of \(X\) and \(Y\) can be calculated as:

\(Cov(X,Y)=E(XY)-\mu_X\mu_Y\)

Proof

In order to prove this theorem, we'll need to use the fact (which you are asked to prove in your homework) that, even in the bivariate situation, expectation is still a linear or distributive operator:

Example 18.1 continued

Suppose again that \(X\) and \(Y\) have the following joint probability mass function:

\( \begin{array}{cc|ccc|c} & f(x, y) & 1 & 2 & 3 & f_{X}(x) \\ \hline x & 1 & 0.25 & 0.25 & 0 & 0.5 \\ & 2 & 0 & 0.25 & 0.25 & 0.5 \\ \hline & f_{Y}(y) & 0.25 & 0.5 & 0.25 & 1 \end{array} \)

Use the theorem we just proved to calculate the covariance of \(X\) and \(Y\).

Solution

Now that we know how to calculate the covariance between two random variables, \(X\) and \(Y\), let's turn our attention to seeing how the covariance helps us calculate what is called the correlation coefficient.

18.2 - Correlation Coefficient of X and Y

The covariance of \(X\) and \(Y\) necessarily reflects the units of both random variables. It is helpful instead to have a dimensionless measure of dependency, such as the correlation coefficient does.

Correlation Coefficient

Let \(X\) and \(Y\) be any two random variables (discrete or continuous!) with standard deviations \(\sigma_X\) and \(\sigma_Y\), respectively. The correlation coefficient of \(X\) and \(Y\), denoted \(\text{Corr}(X,Y)\) or \(\rho_{XY}\) (the greek letter "rho") is defined as:

\(\rho_{XY}=Corr(X,Y)=\dfrac{Cov(X,Y)}{\sigma_X \sigma_Y}=\dfrac{\sigma_{XY}}{\sigma_X \sigma_Y}\)

Example 18-1 (continued)

Suppose that \(X\) and \(Y\) have the following joint probability mass function:

What is the correlation coefficient of \(X\) and \(Y\)?

On the last page, we determined that the covariance between \(X\) and \(Y\) is \(\frac{1}{4}\). And, we are given that the standard deviation of \(X\) is \(\frac{1}{2}\), and the standard deviation of \(Y\) is the square root of \(\frac{1}{2}\). Therefore, it is a straightforward exercise to calculate the correlation between \(X\) and \(Y\) using the formula:

\(\rho_{XY}=\dfrac{\frac{1}{4}}{\left(\frac{1}{2}\right)\left(\sqrt{\frac{1}{2}}\right)}=0.71\)

So now the natural question is "what does that tell us?". Well, we'll be exploring the answer to that question in depth on the page titled More on Understanding Rho, but for now let the following interpretation suffice.

Interpretation of Correlation

On the page titled More on Understanding Rho, we will show that \(-1 \leq \rho_{XY} \leq 1\). Then, the correlation coefficient is interpreted as:

If \(\rho_{XY}=1\), then \(X\) and \(Y\) are perfectly, positively, linearly correlated.
If \(\rho_{XY}=-1\), then \(X\) and \(Y\) are perfectly, negatively, linearly correlated.
If \(\rho_{XY}=0\), then \(X\) and \(Y\) are completely, un-linearly correlated. That is, \(X\) and \(Y\) may be perfectly correlated in some other manner, in a parabolic manner, perhaps, but not in a linear manner.
If \(\rho_{XY}>0\), then \(X\) and \(Y\) are positively, linearly correlated, but not perfectly so.
If \(\rho_{XY}<0\), then \(X\) and \(Y\) are negatively, linearly correlated, but not perfectly so.

So, for our example above, we can conclude that \(X\) and \(Y\) are positively, linearly correlated, but not perfectly so.

18.3 - Understanding Rho

On this page, we'll begin our investigation of what the correlation coefficient tells us. All we'll be doing here is getting a handle on what we can expect of the correlation coefficient if \(X\) and \(Y\) are independent, and what we can expect of the correlation coefficient if \(X\) and \(Y\) are dependent. On the next page, we'll take a more in depth look at understanding the correlation coefficient. Let's start with the following theorem.

Theorem

If \(X\) and \(Y\) are independent random variables (discrete or continuous!), then:

\(Corr(X,Y)=Cov(X,Y)=0\)

Proof

For the sake of this proof, let us assume that \(X\) and \(Y\) are discrete. (The proof that follows can be easily modified if \(X\) and \(Y\) are continuous.) Let's start with the expected value of \(XY\). That is, let's see what we can say about the expected value of \(XY\) if \(X\) and \(Y\) are independent:

That is, we have shown that if \(X\) and \(Y\) are independent, then \(E(XY)=E(X)E(Y)\). Now the rest of the proof follows. If \(X\) and \(Y\) are independent, then:

\begin{align} Cov(X,Y) &=E(XY)-\mu_X\mu_Y\\ &= E(X)E(Y)-\mu_X\mu_Y\\ &= \mu_X\mu_Y-\mu_X\mu_Y=0 \end{align}

and therefore:

\(Corr(X,Y)=\dfrac{Cov(X,Y)}{\sigma_X \sigma_Y}=\dfrac{0}{\sigma_X \sigma_Y}=0\)

Let's take a look at an example of the theorem in action. That is, in the example that follows, we see a case in which \(X\) and \(Y\) are independent and the correlation between \(X\) and \(Y\) is 0.

Example 18-2

Let \(X\) = outcome of a fair, black, 6-sided die. Because the die is fair, we'd expect each of the six possible outcomes to be equally likely. That is, the p.m.f. of \(X\) is:

\(f_X(x)=\dfrac{1}{6},\quad x=1,\ldots,6.\)

Let \(Y\) = outcome of a fair, red, 4-sided die. Again, because the die is fair, we'd expect each of the four possible outcomes to be equally likely. That is, the p.m.f. of \(Y\) is:

\(f_Y(y)=\dfrac{1}{4},\quad y=1,\ldots,4.\)

If we toss the pair of dice, the 24 possible outcomes are (1, 1) (1, 2) ... (1, 4) ... (6, 1) ... (6, 4), with each of the 24 outcomes being equally likely. That is, the joint p.m.f. of \(X\) and \(Y\) is:

\(f(x,y)=\dfrac{1}{24},\quad x=1,2,\ldots,6,\quad y=1,\ldots,4.\)

Although we intuitively feel that the outcome of the black die is independent of the outcome of the red die, we can formally show that \(X\) and \(Y\) are independent:

\(f(x,y)=\dfrac{1}{24}f_X(x)f_Y(y)=\dfrac{1}{6} \cdot \dfrac{1}{4} \qquad \forall x,y\)

What is the covariance of \(X\) and \(Y\) ? What the correlation of \(X\) and \(Y\) ?

Solution

Well, the mean of \(X\) is:

\(\mu_X=E(X)=\sum\limits_x xf(x)=1\left(\dfrac{1}{6}\right)+\cdots+6\left(\dfrac{1}{6}\right)=\dfrac{21}{6}=3.5\)

And, the mean of \(Y\) is:

\(\mu_Y=E(Y)=\sum\limits_y yf(y)=1\left(\dfrac{1}{4}\right)+\cdots+4\left(\dfrac{1}{4}\right)=\dfrac{10}{4}=2.5\)

The expected value of the product \(XY\) is:

\(E(XY)=\sum\limits_x\sum\limits_y xyf(x,y)=(1)(1)\left(\dfrac{1}{24}\right)+(1)(2)\left(\dfrac{1}{24}\right)+\cdots+(6)(4)\left(\dfrac{1}{24}\right)=\dfrac{210}{24}=8.75\)

Therefore, the covariance of \(X\) and \(Y\) is:

\(Cov(X,Y)=E(XY)-\mu_X\mu_Y=8.75-(3.5)(2.5)=8.75-8.75=0\)

and therefore, the correlation between \(X\) and \(Y\) is 0:

\(Corr(X,Y)=\dfrac{Cov(X,Y)}{\sigma_X \sigma_Y}=\dfrac{0}{\sigma_X \sigma_Y}=0\)

Again, this example illustrates a situation in which \(X\) and \(Y\) are independent, and the correlation between \(X\) and \(Y\) is 0, just as the theorem states it should be.

NOTE! the converse of the theorem is not necessarily true! That is, zero correlation and zero covariance do not imply independence. Let's take a look at an example that illustrates this claim.

Example 18-3

Let \(X\) and \(Y\) be discrete random variables with the following joint probability mass function:

What is the correlation between \(X\) and \(Y\)? And, are \(X\) and \(Y\) independent?

Solution

The mean of \(X\) is:

\(\mu_X=E(X)=\sum xf(x)=(-1)\left(\dfrac{2}{5}\right)+(0)\left(\dfrac{1}{5}\right)+(1)\left(\dfrac{2}{5}\right)=0\)

And the mean of \(Y\) is:

\(\mu_Y=E(Y)=\sum yf(y)=(-1)\left(\dfrac{2}{5}\right)+(0)\left(\dfrac{1}{5}\right)+(1)\left(\dfrac{2}{5}\right)=0\)

The expected value of the product \(XY\) is also 0:

\(E(XY)=(-1)(-1)\left(\dfrac{1}{5}\right)+(-1)(1)\left(\dfrac{1}{5}\right)+(0)(0)\left(\dfrac{1}{5}\right)+(1)(-1)\left(\dfrac{1}{5}\right)+(1)(1)\left(\dfrac{1}{5}\right)\)

\(E(XY)=\dfrac{1}{5}-\dfrac{1}{5}+0-\dfrac{1}{5}+\dfrac{1}{5}=0\)

Therefore, the covariance of \(X\) and \(Y\) is 0:

\(Cov(X,Y)=E(XY)-\mu_X\mu_Y=0-(0)(0)=0\)

and therefore the correlation between \(X\) and \(Y\) is necessarily 0.

Yet, \(X\) and \(Y\) are not independent, since the product space is not rectangular! That is, we can find an \(x\) and a \(y\) for which the joint probability mass function \(f(x,y)\) can't be written as the product of \(f(x)\), the probability mass function of \(X\), and \(f(y)\), the probability mass function of \(Y\). For example, when \(x=0\) and \(y=-1\):

\(f(0,-1)=0 \neq f_X(0)f_Y(-1)=(1/5)(2/5)=2/25\)

In summary, again, this example illustrates that if the correlation between \(X\) and \(Y\) is 0, it does not necessarily mean that \(X\) and \(Y\) are independent. On the contrary, we've shown a case here in which the correlation between \(X\) and \(Y\) is 0, and yet \(X\) and \(Y\) are dependent!

The contrapositive of the theorem is always true! That is, if the correlation is not zero, then \(X\) and \(Y\) are dependent. Let's take a look at an example that illustrates this claim.

Example 18-4

A quality control inspector for a t-shirt manufacturer inspects t-shirts for defects. She labels each t-shirt she inspects as either:

"good"
a "second" which could be sold at a reduced price, or
"defective," in which the t-shirt could not be sold at all

The quality control inspector inspects \(n=2\) t-shirts:

Let \(X\) = # of good t-shirts. Historically, the probability that a t-shirt is good is \(p_1=0.6\).
Let \(Y\) = # of second t-shirts. Historically, the probability that a t-shirt is labeled as a second is \(p_2=0.2\).
Let \(2-X-Y\)= # of defective t-shirts. Historically, the probability that a t-shirt is labeled as defective is \(1-p_1-p_2=1-0.6-0.2=0.2\)

Then, the joint probability mass function of \(X\) and \(Y\) is the trinomial distribution. That is:

\(f(x,y)=\dfrac{2!}{x!y!(2-x-y)!} 0.6^x 0.2^y 0.2^{2-x-y},\qquad 0 \leq x+y \leq 2\)

Are \(X\) and \(Y\) independent? And, what is the correlation between \(X\) and \(Y\)?

Solution

First, \(X\) and \(Y\) are indeed dependent, since the support is triangular. Now, for calculating the correlation between \(X\) and \(Y\). The random variable \(X\) is binomial with \(n=2\) and \(p_1=0.6\). Therefore, the mean and standard deviation of \(X\) are 1.2 and 0.69, respectively:

\begin{array}{lcll} X \sim b(2,0.6) & \qquad & \mu_X &=np_1=2(0.6)=1.2\\ & \qquad & \sigma_X &=\sqrt{np_1(1-p_1)}=\sqrt{2(0.6)(0.4)}=0.69 \end{array}

The random variable \(Y\) is binomial with \(n=2\) and \(p_2=0.2\). Therefore, the mean and standard deviation of \(Y\) are 0.4 and 0.57, respectively:

\begin{array}{lcll} Y \sim b(2,0.2) & \qquad & \mu_Y &=np_2=2(0.2)=0.4\\ & \qquad & \sigma_Y &=\sqrt{np_2(1-p_2)}=\sqrt{2(0.2)(0.8)}=0.57 \end{array}

The expected value of the product \(XY\) is:

\begin{align} E(XY)&= \sum\limits_x \sum\limits_y xyf(x,y)\\ &= (1)(1)\dfrac{2!}{1!1!0!} 0.6^1 0.2^1 0.2^0=2(0.6)(0.2)=0.24\\ \end{align}

Therefore, the covariance of \(X\) and \(Y\) is −0.24:

\(Cov(X,Y)=E(XY)-\mu_X\mu_Y=0.24-(1.2)(0.4)=0.24-0.48=-0.24\)

and the correlation between \(X\) and \(Y\) is −0.61:

\(Corr(X,Y)=\dfrac{Cov(X,Y)}{\sigma_X \sigma_Y}=\dfrac{-0.24}{(0.69)(0.57)}=-0.61\)

In summary, again, this is an example in which the correlation between \(X\) and \(Y\) is not 0, and \(X\) and \(Y\) are dependent.

18.4 - More on Understanding Rho

Although we started investigating the meaning of the correlation coefficient, we've still been dancing quite a bit around what exactly the correlation coefficient:

\(Corr(X,Y)=\rho=\dfrac{Cov(X,Y)}{\sigma_X \sigma_Y}=\dfrac{\sum_x\sum_y (x-\mu_X)(y-\mu_Y)f(x,y)}{\sigma_X \sigma_Y}\)

tells us. Since this is the last page of the lesson, I guess there is no more procrastinating! Let's spend this page, then, trying to come up with answers to the following questions:

How does \(\rho_{XY}\) get its sign?
Why is \(\rho_{XY}\) a measure of linear relationship?
Why is \(-1 \leq \rho_{XY} \leq 1\)?
Why does \(\rho_{XY}\) close to −1 or +1 indicate a strong linear relationship?

Question #1

Let's tackle the first question. How does \(\rho_{XY}\) get its sign? Well, we can get a good feel for the answer to that question by simply studying the formula for the correlation coefficient:

The standard deviations \(\sigma_X\) and \(\sigma_Y\) are positive. Therefore, the product \(\sigma_X\sigma_Y\) must also be positive (>0). And, the joint probability mass function must be nonnegative... well, positive (>0) for at least some elements of the support. It is the product:

\((x-\mu_X)(y-\mu_Y)\)

that can be either positive (>0) or negative (<0). That is, the correlation coefficient gets its sign, that is, it is either negative − or positive +, depending on how most of the \((x,y)\) points in the support relate to the \(x=\mu_X\) and \(y=\mu_Y\) lines. Let's take a look at two examples.

Suppose we were interested in studying the relationship between atmospheric pressure \(X\) and the boiling point \(Y\) of water. Then, our plot might look something like this:

The plot suggests that as the atmospheric pressure increases, so does the boiling point of water. Now, what does the plot tell us about the product:

\((x-\mu_X)(y-\mu_Y)\)

Well, it tells us this:

That is, in the upper right quadrant, the difference between any \((x,y)\) data point and the \(x=\mu_X\) line is positive; and the difference between any \((x,y)\) data point and the \(y=\mu_Y\) line is positive. Therefore, any \((x,y)\) data point in the upper right quadrant produces a positive product \((x-\mu_X)(y-\mu_Y)\). Now for the lower left quadrant, where the remaining points lie. In the lower left quadrant, the difference between any \((x,y)\) data point and the \(x=\mu_X\) line is negative; and the difference between any \((x,y)\) data point and the \(y=\mu_Y\) line is negative. Therefore, any \((x,y)\) data point in the lower left quadrant also produces a positive product \((x-\mu_X)(y-\mu_Y)\). So, regardless... every data point in this plots produces a positive product \((x-\mu_X)(y-\mu_Y)\). Therefore, when we add up those positive products over all \(x\) and \(y\), we're going to get a positive correlation coefficient. In general, when there is a positive linear relationship between \(X\) and \(Y\), the sign of the correlation coefficient is going to be positive. Makes intuitive sense!

Now, let's take a look at an example in which the relationship between \(X\) and \(Y\) is negative. Suppose we were interested in studying the relationship between a person's IQ \(X\) and the delinquency index \(Y\) of the person. Well, one researcher investigated the relationship, and published a plot that looked something like this:

The plot suggests that as IQs increase, the delinquency indices decrease. That is, there is an inverse or negative relationship. Now, what does the plot tell us about the product:

\((x-\mu_X)(y-\mu_Y)\)

Well, it tells us this:

That is, in the upper left quadrant, the difference between any \((x,y)\) data point and the \(x=\mu_X\) line is negative; and the difference between any \((x,y)\) data point and the \(y=\mu_Y\) line is positive. Therefore, any \((x,y)\) data point in the upper left quadrant produces a negative product. Now for the lower right quadrant, where most the remaining points lie. In the lower right quadrant, the difference between any \((x,y)\)data point and the \(x=\mu_X\) line is positive; and the difference between any \((x,y)\) data point and the \(y=\mu_Y\) line is negative. Therefore, any \((x,y)\) data point in the lower left quadrant also produces a negative product. Now there are a few data points that lie in the upper right and lower left quadrants that would produce a positive product. But, since most of the data points produce negative products, the sum of the products would still be negative. In general, when there is a negative linear relationship between \(X\) and \(Y\), the sign of the correlation coefficient is going to be negative. Again, makes intuitive sense!

Questions #2, #3, #4

As it turns out, answering the last three questions is going to take a bit of preliminary work before we arrive at the final answers. To make our work concrete, let's suppose that the random variables \(X\) and \(Y\) have a trinomial distribution with \(n=2, p_1=\frac{1}{4}, p_2=\frac{1}{2}\), and \(0\le x+y\le 2\). For trinomial random variables, we typically represent the joint probability mass function as a formula. In this case, let's represent the joint probability mass function as a graph:

Each of the black dots (•) represents an element of the joint support \(S\). As we should expect with a trinomial, the support is triangular. The probabilities that \(X=x\) and \(Y=y\) are indicated in blue. For example, the probability that \(X=0\) and \(Y=1\) is \(\frac{4}{16}\). You can verify these probabilities, if you are so inclined, using the formula for the trinomial p.m.f. What we want to do here, though, is explore the correlation between \(X\) and \(Y\). Now, we'll soon see that we can learn something about the correlation \(\rho_{XY}\) by considering the best fitting line through the \((x,y)\) points in the support. Specifically, consider the best fitting line passing through the point \((\mu_X, \mu_Y)\). We don't yet know what the best fitting line is, but we could "eyeball" such a line on our graph. That's what the red line is here, an "eyeballed" best fitting line:

As the plot suggests, the mean of \(X\) is \(\frac{1}{2}\) and the mean of \(Y\) is 1 (that's because \(X\) is binomial with \(n=2\) and \(p_1=\frac{1}{4}\), and \(Y\) is binomial with \(n=2\) and \(p_2=\frac{1}{2}\)). Now, what we want to do is find the formula for the best (red) fitting line passing through the point \((\mu_X, \mu_Y)\). Well, we know that two points determine a line. So, along with the \((\mu_X, \mu_Y)\) point, let's pick an arbitrary point (x,y) on the line:

Then, we know that the slope of the line is rise over run. That is:

\(slope=\dfrac{rise}{run}=\dfrac{y-\mu_Y}{x-\mu_X}=b\)

and the line is therefore of the form:

\(y-\mu_Y=b(x-\mu_X)\) or \(y=\mu_Y+b(x-\mu_X)\)

Now to find the best fitting line, we'll use the principle of least squares. That is, we'll find the slope \(b\) that minimizes the squared vertical distances between every point \((x_0, y_0)\) in the joint support \(S\) and the point on the line:

\((x_0,\mu_Y+b(x_0-\mu_X))\)

as illustrated here in green:

That is, we need to find the \(b\) that minimizes:

\(K(b)=E\{[(Y-\mu_Y)-b(X-\mu_X)]^2\}\)

The resulting line is called the least squares regression line. What is the least squares regression line?

Solution

Before differentiating, let's start with simplifying the thing that we are trying to minimize:

\(K(b)=E\{[(Y-\mu_Y)-b(X-\mu_X)]^2\}\)

getting:

Now, to find the slope \(b\) that minimizes \(K(b)\), the expected squared vertical distances, we need to differentiate \(K(b)\) with respect to \(b\), and set the resulting derivative to 0. Doing so, we get:

\(K'(b)=-2\rho \sigma_X\sigma_Y + 2b\sigma^2_X \equiv 0\)

Then, solving for \(b\), we first get:

\(b \sigma^2_X=\rho \sigma_X\sigma_Y \)

and then finally:

\(b=\rho \dfrac{\sigma_Y}{\sigma_X}\)

Note that \(b\) does indeed minimize \(K(b)\), because the second derivative of \(K(b)\) is positive. That is:

\(K''(b)=2\sigma^2_X >0\)

Now, we can substitute what we have found for the slope \(b\) into our equation:

\(y=\mu_Y +b(x-\mu_X)\)

getting the least squares regression line:

\(y=\mu_Y + \rho \left(\dfrac{\sigma_Y}{\sigma_X}\right) (x-\mu_X)\)

By the way, note that, because the standard deviations of \(X\) and \(Y\) are positive, if the correlation coefficient \(\rho_{XY}\) is positive, then the slope of the least squares line is also positive. Similarly, if the correlation coefficient \(\rho_{XY}\) is negative, then the slope of the least squares line is also negative.

Now that we've found the \(b\) that minimizes \(K(b)\), what is the value of \(K(b)\) at its minimum \(b=\rho \dfrac{\sigma_Y}{\sigma_X}\)?

Solution

Substituting \(b=\rho \dfrac{\sigma_Y}{\sigma_X}\) into our simplified formula for \(K(b)\):

\(K(b)=\sigma^2_Y-2b\rho \sigma_X\sigma_Y +b^2 \sigma^2_X \)

we get:

\begin{align} K\left(\rho \dfrac{\sigma_Y}{\sigma_X}\right) &= \sigma^2_Y-2\left(\rho \dfrac{\sigma_Y}{\sigma_X}\right)\rho \sigma_X\sigma_Y+\left(\rho \dfrac{\sigma_Y}{\sigma_X}\right)^2 \sigma^2_X \\ &= \sigma^2_Y-2\rho^2 \sigma^2_Y+\rho^2 \sigma^2_Y\\ &= \sigma^2_Y(1-\rho^2) \end{align}

That is:

\(K\left(\rho \dfrac{\sigma_Y}{\sigma_X}\right) =\sigma^2_Y(1-\rho^2)\)

Okay, have we lost sight of what we are doing here? Remember that started way back when trying to answer three questions. Well, all of our hard work now makes the answers to the three questions rather straightforward. Let's take a look!

Why is \(-1 \leq \rho_{XY} \leq 1\)? Well, \(K(b)\) is an expectation of squared terms, so \(K(b)\) is necessarily non-negative. That is:

\(K(b)=\sigma^2_Y(1-\rho^2)\geq 0\)

And because the variance \(\sigma^2_Y\) is necessarily nonnegative, that implies that:

\((1-\rho^2)\geq 0\)

which implies that:

\(-\rho^2 \geq -1\)

which implies that:

\(\rho^2 \leq 1\)

and which finally implies that:

\(-1 \leq \rho \leq 1\)

Phew! Done! We have now answered the third question. Let's now tackle the second and fourth questions. Why is \(\rho_{XY}\) a measure of linearrelationship? And why does \(\rho_{XY}\) close to −1 or +1 indicate a strong linear relationship? Well, we defined \(K(b)\) so that it measures the distance of the points \((x_0,y_0)\) in the joint support \(S\) to a line. Therefore, \(\rho_{XY}\) necessarily must concern a linear relationship, and no other. Now, we can take it a step further. The smaller \(K(b)\) is, the closer the points are to the line:

\(K(b)\) is smallest, 0, when \(\rho_{XY}\) is −1 or +1. In that case, the points fall right on the line, indicating a perfect linear relationship.
\(K(b)\) is largest, \(\sigma^2_Y\) , when \(\rho_{XY}\) is 0. In that case, the points fall far away from the line, indicating a weak linear relationship.

So, there we have it! All four questions posed, and all four questions answered! We should all now have a fairly good understanding of the value of knowing the correlation between two random variables \(X\) and \(Y\).

Lesson 19: Conditional Distributions

Overview

In the last two lessons, we've concerned ourselves with how two random variables \(X\) and \(Y\) behave jointly. We'll now turn to investigating how one of the random variables, say \(Y\), behaves given that another random variable, say \(X\), has already behaved in a certain way. In the discrete case, for example, we might want to know the probability that \(Y\), the number of car accidents in July on a particular curve in the road, equals 2 given that \(X\), the number of cars in June caught speeding on the curve is more than 50. Of course, our previous work investigating conditional probability will help us here. Now, we will extend the idea of conditional probability that we learned previously to the idea of finding a conditional probability distribution of a random variable \(Y\) given another random variable \(X\).

Objectives

Upon completion of this lesson, you should be able to:

To learn the distinction between a joint probability distribution and a conditional probability distribution.
To recognize that a conditional probability distribution is simply a probability distribution for a sub-population.
To learn the formal definition of a conditional probability mass function of a discrete r.v. \(Y\) given a discrete r.v. \(X\).
To learn how to calculate the conditional mean and conditional variance of a discrete r.v. \(Y\) given a discrete r.v. \(X\).
To be able to apply the methods learned in the lesson to new problems.

19.1 - What is a Conditional Distribution?

Let's start our investigation of conditional distributions by using an example to help enlighten us about the distinction between a joint (bivariate) probability distribution and a conditional probability distribution.

Example 19-1

A Safety Officer for an auto insurance company in Connecticut was interested in learning how the extent of an individual's injury in an automobile accident relates to the type of safety restraint the individual was wearing at the time of the accident. As a result, the Safety Officer used statewide ambulance and police records to compile the following two-way table of joint probabilities:

f (x,y)	Type of Restraint (Y)
Extent of Injury (X)	None (0)	Belt Only (1)	Belt and Harness (2)	fx(x)
None (0)	0.065	0.075	0.06	0.20
Minor (1)	0.175	0.16	0.115	0.45
Major (2)	0.135	0.10	0.065	0.30
Death (3)	0.025	0.015	0.01	0.05
f_Y(y)	0.40	0.35	0.25	1.00

For the sake of understanding the Safety Officer's terminology, let's assume that "Belt only" means that the person was only using the lap belt, whereas "Belt and Harness" should be taken to mean that the person was using a lap belt and shoulder strap. (These data must have been collected a loooonnnggg time ago when such an option was legal!) Also, note that the Safety Officer created the random variable \(X\), the extent of injury, by arbitrarily assigning values 0, 1, 2, and 3 to each of the possible outcomes None, Minor, Major, and Death. Similarly, the Safety Officer created the random variable \(Y\), the type of restraint, by arbitrarily assigning values 0, 1, and 2 to each of the possible outcomes None, Belt Only, and Belt and Harness.

Among other things, the Safety Officer was interested in answering the following questions:

What is the probability that a randomly selected person in an automobile accident was wearing a seat belt and had only a minor injury?
If a randomly selected person wears no restraint, what is the probability of death?
If a randomly selected person sustains no injury, what is the probability the person was wearing a belt and harness?

Before we can help the Safety Officer answer his questions, we could benefit from a couple of (informal) definitions under our belt.

Definition

A joint (bivariate) probability distribution describes the probability that a randomly selected person from the population has the two characteristics of interest.

There is actually nothing really new here. We should know by now not only informally, but also formally, the definition of a bivariate probability distribution.

Example (continued)

What is the probability a randomly selected person in an accident was wearing a seat belt and had only a minor injury?

Solution

Let \(A\) = the event that a randomly selected person in a car accident has a minor injury. Let \(B\) = the event that the randomly selected person was wearing only a seat belt. Then, just reading the value right off of the Safety Officer's table, we get:

\(P(A\text{ and }B)=P(X=1, Y=1)=f(1, 1)=0.16\)

That is, there is a 16% chance that a randomly selected person in an accident is wearing a seat belt and has only a minor injury.

Now, of course, in order to define the joint probability distribution of \(X\) and \(Y\) fully, we'd need to find the probability that \(X=x\) and \(Y=y\) for each element in the joint support \(S\), not just for one element \(X=1\) and \(Y=1\). But, that's not our point here. Here, we are revisiting the meaning of the joint probability distribution of \(X\) and \(Y\) just so we can distinguish between it and a conditional probability distribution.

Conditional Probability Distribution: A conditional probability distribution is a probability distribution for a sub-population. That is, a conditional probability distribution describes the probability that a randomly selected person from a sub-population has the one characteristic of interest.

Example (continued)

If a randomly selected person wears no restraint, what is the probability of death?

Solution

As you can see, the Safety Officer is wanting to know a conditional probability. So, we need to use the definition of conditional probability to calculate the desired probability. But, let's first dissect the Safety Officer's question into two parts by identifying the subpopulation and the characteristic of interest. Well, the subpopulation is the population of people wearing no restraints ( \(NR\) ), and the characteristic of interest is death (\(D\)). Then, using the definition of conditional probability, we determine that the desired probability is:

\(P(D|NR)=\dfrac{P(D \cap NR)}{P(NR)}=\dfrac{P(X=3,Y=0)}{P(Y=0)}=\dfrac{f(3,0)}{f_Y(0)}=\dfrac{0.025}{0.40}=0.0625\)

That is, there is a 6.25% chance of death of a randomly selected person in an automobile accident, if the person wears no restraint.

In order to define the conditional probability distribution of \(X\) given \(Y\) fully, we'd need to find the probability that \(X=x\) given \(Y=y\) for each element in the joint support \(S\), not just for one element \(X=3\) and \(Y=0\). But, again, that's not our point here. Here, we are simply trying to get the feel of how a conditional probability distribution describes the probability that a randomly selected person from a sub-population has the one characteristic of interest.

Example (continued)

If a randomly selected person sustains no injury, what is the probability the person was wearing a seatbelt and harness?

Solution

Again, the Safety Officer is wanting to know a conditional probability. Let's again first dissect the Safety Officer's question into two parts by identifying the subpopulation and the characteristic of interest. Well, here, the subpopulation is the population of people sustaining no injury (\(NI\)), and the characteristic of interest is wearing a seatbelt and harness (\(SH\)). Then, again using the definition of conditional probability, we determine that the desired probability is:

\(P(SH|NI)=\dfrac{P(SH \cap NI)}{P(NI)}=\dfrac{P(X=0,Y=2)}{P(X=0)}=\dfrac{f(0,2)}{f_X(0)}=\dfrac{0.06}{0.20}=0.30\)

That is, there is a 30% chance that a randomly selected person in an automobile accident is wearing a seatbelt and harness, if the person sustains no injury.

Again, in order to define the conditional probability distribution of \(Y\) given \(X\) fully, we'd need to find the probability that \(Y=y\) given \(X=x\) for each element in the joint support of \(S\), not just for one element \(X=0\) and \(Y=2\). But, again, that's not our point here. Here, we are again simply trying to get the feel of how a conditional probability distribution describes the probability that a randomly selected person from a sub-population has the one characteristic of interest.

19.2 - Definitions

Now that we've digested the concept of a conditional probability distribution informally, let's now define it formally for discrete random variables \(X\) and \(Y\). Later, we'll extend the definition for continuous random variables \(X\) and \(Y\).

Conditional probability mass function of \(X\)

The conditional probability mass function of \(X\), given that \(Y=y\), is defined by:

\(g(x|y)=\dfrac{f(x,y)}{f_Y(y)}\qquad \text{provided} f_Y(y)>0\)

Similarly,

Conditional probability mass function of \(Y\)

The conditional probability mass function of \(Y\), given that \(X=x\), is defined by:

\(h(y|x)=\dfrac{f(x,y)}{f_X(x)}\qquad \text{provided} f_X(x)>0\)

Let's get some practice using the definition to find the conditional probability distribution first of \(X\) given \(Y\), and then of \(Y\) given \(X\).

Example 19-2

Let \(X\) be a discrete random variable with support \(S_1=\{0,1\}\), and let \(X\) be a discrete random variable with support \(S_2=\{0, 1, 2\}\). Suppose, in tabular form, that \(X\) and \(Y\) have the following joint probability distribution \(f(x,y)\):

What is the conditional distribution of \(X\) given \(Y\)? That is, what is \(g(x|y)\)?

Solution

Using the formula \(g(x|y)=\dfrac{f(x,y)}{f_Y(y)}\), with \(x=0\) and 1, and \(y=0, 1\), and 2, the conditional distribution of \(X\) given \(Y\) is, in tabular form:

For example, the 1/3 in the \(x=0\) and \(y=0\) cell comes from:

That is:

\(g(0|0)=\dfrac{f(0,0)}{f_Y(0)}=\dfrac{1/8}{3/8}=\dfrac{1}{3}\)

And, the 2/3 in the \(x=1\) and \(y=0\) cell comes from:

That is:

\(g(1|0)=\dfrac{f(1,0)}{f_Y(0)}=\dfrac{2/8}{3/8}=\dfrac{2}{3}\)

The remaining conditional probabilities are calculated in a similar way. Note that the conditional probabilities in the \(g(x|y)\) table are color-coded as blue when y = 0, red when y = 1, and green when y = 2. That isn't necessary, of course, but rather just a device used to emphasize the concept that the probabilities that \(X\) takes on a particular value are given for the three different sub-populations defined by the value of \(Y\).

Note also that it shouldn't be surprising that for each of the three sub-populations defined by \(Y\), if you add up the probabilities that \(X=0\) and \(X=1\), you always get 1. This is just as we would expect if we were adding up the (marginal) probabilities over the support of \(X\). It's just that here we have to do it for each sub-population rather than the entire population!

Let \(X\) be a discrete random variable with support \(S_1=\{0,1\}\), and let \(Y\) be a discrete random variable with support \(S_2=\{0, 1, 2\}\). Suppose, in tabular form, that \(X\) and \(Y\) have the following joint probability distribution \(f(x,y)\):

What is the conditional distribution of \(Y\) given \(X\)? That is, what is \(h(y|x)\)?

Solution

Using the formula \(h(y|x)=\dfrac{f(x,y)}{f_X(x)}\), with \(x=0\) and 1, and \(y=0, 1\), and 2, the conditional distribution of \(Y\) given \(X\) is, in tabular form:

For example, the 1/4 in the \(x=0\) and \(y=0\) cell comes from:

That is:

\(h(0|0)=\dfrac{f(0,0)}{f_X(0)}=\dfrac{1/8}{4/8}=\dfrac{1}{4}\)

And, the 2/4 in the \(x=0\) and \(y=1\) cell comes from:

That is:

\(h(1|0)=\dfrac{f(0,1)}{f_X(0)}=\dfrac{2/8}{4/8}=\dfrac{2}{4}\)

And, the 1/4 in the \(x=0\) and \(y=2\) cell comes from:

That is:

\(h(2|0)=\dfrac{f(0,2)}{f_X(0)}=\dfrac{1/8}{4/8}=\dfrac{1}{4}\)

Again, the remaining conditional probabilities are calculated in a similar way. Note that the conditional probabilities in the \(h(y|x)\) table are color-coded as blue when x = 0 and red when x = 1. Again, that isn't necessary, but rather just a device used to emphasize the concept that the probabilities that \(Y\) takes on a particular value are given for the two different sub-populations defined by the value of \(X\).

Note also that it shouldn't be surprising that for each of the two subpopulations defined by \(X\), if you add up the probabilities that \(Y=0\), \(Y=1\), and \(Y=2\), you get a total of 1. This is just as we would expect if we were adding up the (marginal) probabilities over the support of \(Y\). It's just that here, again, we have to do it for each sub-population rather than the entire population!

Okay, now that we've determined \(h(y|x)\), the conditional distribution of \(Y\) given \(X\), and \(g(x|y)\), the conditional distribution of \(X\) given \(Y\), you might also want to note that \(g(x|y)\) does not equal \(h(y|x)\). That is, in general, almost always the case.

So, we've used the definition to find the conditional distribution of \(X\) given \(Y\), as well as the conditional distribution of \(Y\) given \(X\). We should now have enough experience with conditional distributions to believe that the following two statements true:

Conditional distributions are valid probability mass functions in their own right. That is, the conditional probabilities are between 0 and 1, inclusive:

\(0 \leq g(x|y) \leq 1 \qquad \text{and}\qquad 0 \leq h(y|x) \leq 1 \)

and, for each subpopulation, the conditional probabilities sum to 1:

\(\sum\limits_x g(x|y)=1 \qquad \text{and}\qquad \sum\limits_y h(y|x)=1 \)
In general, the conditional distribution of \(X\) given \(Y\) does not equal the conditional distribution of \(Y\) given \(X\). That is:

\(g(x|y)\ne h(y|x)\)

19.3 - Conditional Means and Variances

Now that we've mastered the concept of a conditional probability mass function, we'll now turn our attention to finding conditional means and variances. We'll start by giving formal definitions of the conditional mean and conditional variance when \(X\) and \(Y\) are discrete random variables. And then we'll end by actually calculating a few!

Definition. Suppose \(X\) and \(Y\) are discrete random variables. Then, the conditional mean of \(Y\) given \(X=x\) is defined as:

\(\mu_{Y|X}=E[Y|x]=\sum\limits_y yh(y|x)\)

And, the conditional mean of \(X\) given \(Y=y\) is defined as:

\(\mu_{X|Y}=E[X|y]=\sum\limits_x xg(x|y)\)

The conditional variance of \(Y\) given \(X=x\) is:

\(\sigma^2_{Y|x}=E\{[Y-\mu_{Y|x}]^2|x\}=\sum\limits_y [y-\mu_{Y|x}]^2 h(y|x)\)

or, alternatively, using the usual shortcut:

\(\sigma^2_{Y|x}=E[Y^2|x]-\mu^2_{Y|x}=\left[\sum\limits_y y^2 h(y|x)\right]-\mu^2_{Y|x}\)

And, the conditional variance of \(X\) given \(Y=y\) is:

\(\sigma^2_{X|y}=E\{[X-\mu_{X|y}]^2|y\}=\sum\limits_x [x-\mu_{X|y}]^2 g(x|y)\)

or, alternatively, using the usual shortcut:

\(\sigma^2_{X|y}=E[X^2|y]-\mu^2_{X|y}=\left[\sum\limits_x x^2 g(x|y)\right]-\mu^2_{X|y}\)

As you can see by the formulas, a conditional mean is calculated much like a mean is, except you replace the probability mass function with a conditional probability mass function. And, a conditional variance is calculated much like a variance is, except you replace the probability mass function with a conditional probability mass function. Let's return to one of our examples to get practice calculating a few of these guys.

Example 19-3

Let \(X\) be a discrete random variable with support \(S_1=\{0,1\}\), and let \(Y\) be a discrete random variable with support \(S_2=\{0, 1, 2\}\). Suppose, in tabular form, that \(X\) and \(Y\) have the following joint probability distribution \(f(x,y)\):

What is the conditional mean of \(Y\) given \(X=x\)?

Solution

We previously determined that the conditional distribution of \(Y\) given \(X\) is:

Therefore, we can use it, that is, \(h(y|x)\), and the formula for the conditional mean of \(Y\) given \(X=x\) to calculate the conditional mean of \(Y\) given \(X=0\). It is:

\(\mu_{Y|0}=E[Y|0]=\sum\limits_y yh(y|0)=0\left(\dfrac{1}{4}\right)+1\left(\dfrac{2}{4}\right)+2\left(\dfrac{1}{4}\right)=1\)

And, we can use \(h(y|x)\) and the formula for the conditional mean of \(Y\) given \(X=x\) to calculate the conditional mean of \(Y\) given \(X=1\). It is:

\(\mu_{Y|1}=E[Y|1]=\sum\limits_y yh(y|1)=0\left(\dfrac{2}{4}\right)+1\left(\dfrac{1}{4}\right)+2\left(\dfrac{1}{4}\right)=\dfrac{3}{4}\)

Note that the conditional mean of \(Y|X=x\) depends on \(x\), and depends on \(x\) alone. You might want to think about these conditional means in terms of sub-populations again. The mean of \(Y\) is likely to depend on the sub-population, as it does here. The mean of \(Y\) is 1 for the \(X=0\) sub-population, and the mean of \(Y\) is \(\frac{3}{4}\) for the \(X=1\) sub-population. Intuitively, this dependence should make sense. Rather than calculating the average weight of an adult, for example, you would probably want to calculate the average weight for the sub-population of females and the average weight for the sub-population of males, because the average weight no doubt depends on the sub-population!

What is the conditional mean of \(X\) given \(Y=y\)?

Solution

We previously determined that the conditional distribution of \(X\) given \(Y\) is:

As the conditional distribution of \(X\) given \(Y\) suggests, there are three sub-populations here, namely the \(Y=0\) sub-population, the \(Y=1\) sub-population and the \(Y=2\) sub-population. Therefore, we have three conditional means to calculate, one for each sub-population. Now, we can use \(g(x|y)\) and the formula for the conditional mean of \(X\) given \(Y=y\) to calculate the conditional mean of \(X\) given \(Y=0\). It is:

\(\mu_{X|0}=E[X|0]=\sum\limits_x xg(x|0)=0\left(\dfrac{1}{3}\right)+1\left(\dfrac{2}{3}\right)=\dfrac{2}{3}\)

And, we can use \(g(x|y)\) and the formula for the conditional mean of \(X\) given \(Y=y\) to calculate the conditional mean of \(X\) given \(Y=1\). It is:

\(\mu_{X|1}=E[X|1]=\sum\limits_x xg(x|1)=0\left(\dfrac{2}{3}\right)+1\left(\dfrac{1}{3}\right)=\dfrac{1}{3}\)

And, we can use \(g(x|y)\) and the formula for the conditional mean of \(X\) given \(Y=y\) to calculate the conditional mean of \(X\) given \(Y=2\). It is:

\(\mu_{X|2}=E[X|2]=\sum\limits_x xg(x|2)=0\left(\dfrac{1}{2}\right)+1\left(\dfrac{1}{2}\right)=\dfrac{1}{2}\)

Note that the conditional mean of \(X|Y=y\) depends on \(y\), and depends on \(y\) alone. The mean of \(X\) is \(\frac{2}{3}\) for the \(Y=0\) sub-population, the mean of \(X\) is \(\frac{1}{3}\) for the \(Y=1\) sub-population, and the mean of \(X\) is \(\frac{1}{2}\) for the \(Y=2\) sub-population.

What is the conditional variance of \(Y\) given \(X=0\)?

Solution

We previously determined that the conditional distribution of \(Y\) given \(X\) is:

Therefore, we can use it, that is, \(h(y|x)\), and the formula for the conditional variance of \(X\) given \(X=x\) to calculate the conditional variance of \(X\) given \(X=0\). It is:

\begin{align} \sigma^2_{Y|0} &= E\{[Y-\mu_{Y|0}]^2|x\}=E\{[Y-1]^2|0\}=\sum\limits_y (y-1)^2 h(y|0)\\ &= (0-1)^2 \left(\dfrac{1}{4}\right)+(1-1)^2 \left(\dfrac{2}{4}\right)+(2-1)^2 \left(\dfrac{1}{4}\right)=\dfrac{1}{4}+0+\dfrac{1}{4}=\dfrac{2}{4} \end{align}

We could have alternatively used the shortcut formula. Doing so, we better get the same answer:

\begin{align} \sigma^2_{Y|0} &= E[Y^2|0]-\mu_{Y|0}]^2=\left[\sum\limits_y y^2 h(y|0)\right]-1^2\\ &= \left[(0)^2\left(\dfrac{1}{4}\right)+(1)^2\left(\dfrac{2}{4}\right)+(2)^2\left(\dfrac{1}{4}\right)\right]-1\\ &= \left[0+\dfrac{2}{4}+\dfrac{4}{4}\right]-1=\dfrac{2}{4} \end{align}

And we do! That is, no matter how we choose to calculate it, we get that the variance of \(Y\) is \(\frac{1}{2}\) for the \(X=0\) sub-population.

Lesson 20: Distributions of Two Continuous Random Variables

Overview

In some cases, \(X\) and \(Y\) may both be continuous random variables. For example, suppose \(X\) denotes the duration of an eruption (in second) of Old Faithful Geyser, and \(Y\) denotes the time (in minutes) until the next eruption. We might want to know if there is a relationship between \(X\) and \(Y\). Or, we might want to know the probability that \(X\) falls between two particular values \(a\) and \(b\), and \(Y\) falls between two particular values \(c\) and \(d\). That is, we might want to know \(P(a<x<b, c<Y<d)\).

Objectives

Upon completion of this lesson, you should be able to:

To learn the formal definition of a joint probability density function of two continuous random variables.
To learn how to use a joint probability density function to find the probability of a specific event.
To learn how to find a marginal probability density function of a continuous random variable \(X\) from the joint probability density function of \(X\) and \(Y\).
To learn how to find the means and variances of the continuous random variables \(X\) and \(Y\) using their joint probability density function.
To learn the formal definition of a conditional probability density function of a continuous r.v. \(Y\) given a continuous r.v. \(X\).
To learn how to calculate the conditional mean and conditional variance of a continuous r.v. \(Y\) given a continuous r.v. \(X\).
To be able to apply the methods learned in the lesson to new problems.

20.1 - Two Continuous Random Variables

So far, our attention in this lesson has been directed towards the joint probability distribution of two or more discrete random variables. Now, we'll turn our attention to continuous random variables. Along the way, always in the context of continuous random variables, we'll look at formal definitions of joint probability density functions, marginal probability density functions, expectation and independence. We'll also apply each definition to a particular example.

Joint probability density function: Let \(X\) and \(Y\) be two continuous random variables, and let \(S\) denote the two-dimensional support of \(X\) and \(X\). Then, the function \(f(x,y)\) is a joint probability density function (abbreviated p.d.f.) if it satisfies the following three conditions:
\(f(x,y)\geq 0\) \(\int_{-\infty}^\infty \int_{-\infty}^\infty f(x,y)dxdy=1\) \(P[(X,Y) \in A]=\int\int_A f(x,y)dxdy \) where {(X, Y) ∈ A} is an event in the xy-plane.

The first condition, of course, just tells us that the function must be nonnegative. Keeping in mind that \(f(x,y)\) is some two-dimensional surface floating above the \(xy\)-plane, the second condition tells us that, the volume defined by the support, the surface and the \(xy\)-plane must be 1. The third condition tells us that in order to determine the probability of an event \(A\), you must integrate the function \(f(x,y)\) over the space defined by the event \(A\). That is, just as finding probabilities associated with one continuous random variable involved finding areas under curves, finding probabilities associated with two continuous random variables involves finding volumes of solids that are defined by the event \(A\) in the \(xy\)-plane and the two-dimensional surface \(f(x,y)\).

Example 20-1

Let \(X\) and \(Y\) have joint probability density function:

\(f(x,y)=4xy\)

for \(0<x<1\) and \(0<y<1\). Is \(f(x,y)\) a valid p.d.f.?

Solution

Before trying to verify that \(f(x,y)\) is a valid p.d.f., it might help to get a feel for what the function looks like. Here's my attempt at a sketch of the function:

The red square is the joint support of \(X\) and \(Y\) that lies in the \(xy\)-plane. The blue tent-shaped surface is my rendition of the \(f(x,y)\) surface. Now, in order to verify that \(f(x,y)\) is a valid p.d.f., we first need to show that \(f(x,y)\) is always non-negative. Clearly, that's the case, as it lies completely above the \(xy\)-plane. If you're still not convinced, you can see that in substituting any \(x\) and \(y\) value in the joint support into the function \(f(x,y)\), you always get a positive value.

Now, we just need to show that the volume of the solid defined by the support, the \(xy\)-plane and the surface is 1:

What is \(P(Y<X)\)?

Solution

In order to find the desired probability, we again need to find a volume of a solid as defined by the surface, the \(xy\)-plane, and the support. This time, however, the volume is not defined in the \(xy\)-plane by the unit square. Instead, the region in the \(xy\)-plane is constrained to be just that portion of the unit square for which \(y<x\). If we start with the support \(0<x<1\) and \(0<y<1\) (the red square), and find just the portion of the red square for which \(y<x\), we get the blue triangle:

So, it's the volume of the solid between the \(f(x,y)\) surface and the blue triangle that we need to find. That is, to find the desired volume, that is, the desired probability, we need to integrate from \(y=0\) to \(x\), and then from \(x=0\) to 1:

Given the symmetry of the solid about the plane \(y=x\), perhaps we shouldn't be surprised to discover that our calculated probability equals \(\frac{1}{2}\)!

Marginal Probability Density Functions

The marginal probability density functions of the continuous random variables \(X\) and \(Y\) are given, respectively, by:

\(f_X(x)=\int_{-\infty}^\infty f(x,y)dy,\qquad x\in S_1\)

and:

\(f_Y(y)=\int_{-\infty}^\infty f(x,y)dx,\qquad y\in S_2\)

where \(S_1\) and \(S_2\) are the respective supports of \(X\) and \(Y\).

Example (continued)

Let \(X\) and \(Y\) have joint probability density function:

\(f(x,y)=4xy\)

for \(0<x<1\) and \(0<y<1\). What is \(f_X(x)\), the marginal p.d.f. of \(X\), and \(f_Y(y)\), the marginal p.d.f. of \(Y\)?

Solution

In order to find the marginal p.d.f. of \(X\), we need to integrate the joint p.d.f. \(f(x,y)\) over \(0<y<1\), that is, over the support of \(Y\). Doing so, we get:

\(f_X(x)=\int_0^1 4xy dy=4x\left[\dfrac{y^2}{2}\right]_{y=0}^{y=1}=2x, \qquad 0<x<1\)

In order to find the marginal p.d.f. of \(Y\), we need to integrate the joint p.d.f. \(f(x,y)\) over \(0<x<1\), that is, over the support of \(X\). Doing so, we get:

\(f_Y(y)=\int_0^1 4xy dx=4y\left[\dfrac{x^2}{2}\right]_{x=0}^{x=1}=2y, \qquad 0<y<1\)

Definition. The expected value of a continuous random variable \(X\) can be found from the joint p.d.f of \(X\) and \(Y\) by:

\(E(X)=\int_{-\infty}^\infty \int_{-\infty}^\infty xf(x,y)dxdy\)

Similarly, the expected value of a continuous random variable \(Y\) can be found from the joint p.d.f of \(X\) and \(Y\) by:

\(E(Y)=\int_{-\infty}^\infty \int_{-\infty}^\infty yf(x,y)dydx\)

Example (continued)

Let \(X\) and \(Y\) have joint probability density function:

\(f(x,y)=4xy\)

for \(0<x<1\) and \(0<y<1\). What is the expected value of \(X\)? What is the expected value of \(Y\)?

Solution

The expected value of \(X\) is \(\frac{2}{3}\) as is found here:

We'll leave it to you to show, not surprisingly, that the expected value of \(Y\) is also \(\frac{2}{3}\).

Definition. The continuous random variables \(X\) and \(Y\) are independent if and only if the joint p.d.f. of \(X\) and \(Y\) factors into the product of their marginal p.d.f.s, namely:

\(f(x,y)=f_X(x)f_Y(y), \qquad x\in S_1, \qquad y\in S_2\)

Example (continued)

Let \(X\) and \(Y\) have joint probability density function:

\(f(x,y)=4xy\)

for \(0<x<1\) and \(0<y<1\). Are \(X\) and \(Y\) independent?

Solution

The random variables \(X\) and \(Y\) are indeed independent, because:

\(f(x,y)=4xy=f_X(x) f_Y(y)=(2x)(2y)=4xy\)

So, this is an example in which the support is "rectangular" and \(X\) and \(Y\) are independent.

Note that, as is true in the discrete case, if the support \(S\) of \(X\) and \(Y\) is "triangular," then \(X\) and \(Y\) cannot be independent. On the other hand, if the support is "rectangular" (that is, a product space), then \(X\) and \(Y\) may or may not be independent. Let's take a look first at an example in which we have a triangular support, and then at an example in which the support is rectangular, and, unlike the previous example, \(X\) and \(Y\) are dependent.

Example 20-2

Let \(X\) and \(Y\) have joint probability density function:

\(f(x,y)=x+y\)

for \(0<x<1\) and \(0<y<1\). Are \(X\) and \(Y\) independent?

Solution

Again, in order to show that \(X\) and \(Y\) are independent, we need to be able to show that the joint p.d.f. of \(X\) and \(Y\) factors into the product of the marginal p.d.f.s. The marginal p.d.f. of \(X\) is:

\(f_X(x)=\int_0^1(x+y)dy=\left[xy+\dfrac{y^2}{2}\right]^{y=1}_{y=0}=x+\dfrac{1}{2},\qquad 0<x<1\)

And, the marginal p.d.f. of \(Y\) is:

\(f_Y(y)=\int_0^1(x+y)dx=\left[xy+\dfrac{x^2}{2}\right]^{x=1}_{x=0}=y+\dfrac{1}{2},\qquad 0<y<1\)

Clearly, \(X\) and \(Y\) are dependent, because:

\(f(x,y)=x+y\neq f_X(x) f_Y(y)=\left(x+\dfrac{1}{2}\right) \left(y+\dfrac{1}{2}\right)\)

This is an example in which the support is rectangular:

and \(X\) and \(Y\) are dependent, as we just illustrated. Again, a rectangular support may or may not lead to independent random variables.

20.2 - Conditional Distributions for Continuous Random Variables

Thus far, all of our definitions and examples concerned discrete random variables, but the definitions and examples can be easily modified for continuous random variables. That's what we'll do now!

Conditional Probability Density Function of \(Y\) given \(X=x\)

Suppose \(X\) and \(Y\) are continuous random variables with joint probability density function \(f(x,y)\) and marginal probability density functions \(f_X(x)\) and \(f_Y(y)\), respectively. Then, the conditional probability density function of \(Y\) given \(X=x\) is defined as:

\(h(y|x)=\dfrac{f(x,y)}{f_X(x)}\)

provided \(f_X(x)>0\). The conditional mean of \(Y\) given \(X=x\) is defined as:

\(E(Y|x)=\int_{-\infty}^\infty yh(y|x)dy\)

The conditional variance of \(Y\) given \(X=x\) is defined as:

\(Var(Y|x)=E\{[Y-E(Y|x)]^2|x\}=\int_{-\infty}^\infty [y-E(Y|x)]^2 h(y|x)dy\)

or, alternatively, using the usual shortcut:

\(Var(Y|x)=E[Y^2|x]-[E(Y|x)]^2=\left[\int_{-\infty}^\infty y^2h(y|x)dy\right]-\mu^2_{Y|x}\)

Although the conditional p.d.f., mean, and variance of \(X\), given that \(Y=y\), is not given, their definitions follow directly from those above with the necessary modifications. Let's take a look at an example involving continuous random variables.

Example 20-3

Suppose the continuous random variables \(X\) and \(Y\) have the following joint probability density function:

\(f(x,y)=\dfrac{3}{2}\)

for \(x^2\le y\le 1\) and \(0<x<1\). What is the conditional distribution of \(Y\) given \(X=x\)?

Solution

We can use the formula:

\(h(y|x)=\dfrac{f(x,y)}{f_X(x)}\)

to find the conditional p.d.f. of \(Y\) given \(X\). But, to do so, we clearly have to find \(f_X(x)\), the marginal p.d.f. of \(X\) first. Recall that we can do that by integrating the joint p.d.f. \(f(x,y)\) over \(S_2\), the support of \(Y\). Here's what the joint support \(S\) looks like:

So, we basically have a plane, shaped like the support, floating at a constant \(\frac{3}{2}\) units above the \(xy\)-plane. To find \(f_X(x)\) then, we have to integrate:

\(f(x,y)=\dfrac{3}{2}\)

over the support \(x^2\le y\le 1\). That is:

\(f_X(x)=\int_{S_2}f(x,y)dy=\int^1_{x^2} 3/2dy=\left[\dfrac{3}{2}y\right]^{y=1}_{y=x^2}=\dfrac{3}{2}(1-x^2)\)

for \(0<x<1\). Now, we can use the joint p.d.f \(f(x,y)\) that we were given and the marginal p.d.f. \(f_X(x)\) that we just calculated to get the conditional p.d.f. of \(Y\) given \(X=x\):

\( h(y|x)=\dfrac{f(x,y)}{f_X(x)}=\dfrac{\frac{3}{2}}{\frac{3}{2}(1-x^2)}=\dfrac{1}{(1-x^2)},\quad 0<x<1,\quad x^2 \leq y \leq 1\)

That is, given \(x\), the continuous random variable \(Y\) is uniform on the interval \((x^2, 1)\). For example, if \(x=\frac{1}{4}\), then the conditional p.d.f. of \(Y\) is:

\( h(y|1/4)=\dfrac{1}{1-(1/4)^2}=\dfrac{1}{(15/16)}=\dfrac{16}{15}\)

for \(\frac{1}{16}\le y\le 1\). And, if \(x=\frac{1}{2}\), then the conditional p.d.f. of \(Y\) is:

\( h(y|1/2)=\dfrac{1}{1-(1/2)^2}=\dfrac{1}{1-(1/4)}=\dfrac{4}{3}\)

for \(\frac{1}{4}\le y\le 1\).

What is the conditional mean of \(Y\) given \(X=x\)?

Solution

We can find the conditional mean of \(Y\) given \(X=x\) just by using the definition in the continuous case. That is:

Note that given that the conditional distribution of \(Y\) given \(X=x\) is the uniform distribution on the interval \((x^2,1)\), we shouldn't be surprised that the expected value looks like the expected value of a uniform random variable!

Let's take the case where \(x=\frac{1}{2}\). We previously showed that the conditional distribution of \(Y\) given \(X=\frac{1}{2}\) is

\( h(y|1/2)=\dfrac{1}{1-(1/2)^2}=\dfrac{1}{1-(1/4)}=\dfrac{4}{3}\)

for \(\frac{1}{4}\le y\le 1\). Now, we know that the conditional mean of \(Y\) given \(X=\frac{1}{2}\) is:

\(E(Y|\dfrac{1}{2})=\dfrac{1+(1/2)^2}{2}=\dfrac{1+(1/4)}{2}=\dfrac{5}{8}\)

If we think again of the expected value as the fulcrum at which the probability mass is balanced, our results here make perfect sense:

Lesson 21: Bivariate Normal Distributions

Overview

Let the random variable \(Y\) denote the weight of a randomly selected individual, in pounds. Then, suppose we are interested in determining the probability that a randomly selected individual weighs between 140 and 160 pounds. That is, what is \(P(140<Y<160)\)?

But, if we think about it, we could imagine that the weight of an individual increases (linearly?) as height increases. If that's the case, in calculating the probability that a randomly selected individual weighs between 140 and 160 pounds, we might find it more informative to first take into account a person's height, say \(X\). That is, we might want to find instead \(P(140<Y<160|X=x)\). To calculate such a conditional probability, we clearly first need to find the conditional distribution of \(Y\) given \(X=x\). That's what we'll do in this lesson, that is, after first making a few assumptions.

First, we'll assume that (1) \(Y\) follows a normal distribution, (2) \(E(Y|x)\), the conditional mean of \(Y\) given \(x\) is linear in \(x\), and (3) \(\text{Var}(Y|x)\), the conditional variance of \(Y\) given \(x\) is constant. Based on these three stated assumptions, we'll find the conditional distribution of \(Y\) given \(X=x\).

Then, to the three assumptions we've already made, we'll then add the assumption that the random variable \(X\) follows a normal distribution, too. Based on the now four stated assumptions, we'll find the joint probability density function of \(X\) and \(Y\).

Objectives

Upon completion of this lesson, you should be able to:

To find the conditional distribution of \(Y\) given \(X=x\), assuming that (1) \(Y\) follows a normal distribution, (2) \(E(Y|x)\), the conditional mean of \(Y\) given \(x\) is linear in \(x\), and (3) \(\text{Var}(Y|x)\), the conditional variance of \(Y\) given \(x\) is constant.
To learn how to calculate conditional probabilities using the resulting conditional distribution.
To find the joint distribution of \(X\) and \(Y\) assuming that (1) \(X\) follows a normal distribution, (2) \(Y\) follows a normal distribution, (3) \(E(Y|x)\), the conditional mean of \(Y\) given \(x\) is linear in \(x\), and (4) \(\text{Var}(Y|x)\), the conditional variance of \(Y\) given \(x\) is constant.
To learn the formal definition of the bivariate normal distribution.
To understand that when \(X\) and \(Y\) have the bivariate normal distribution with zero correlation, then \(X\) and \(Y\) must be independent.
To understand each of the proofs provided in the lesson.
To be able to apply the methods learned in the lesson to new problems.

21.1 - Conditional Distribution of Y Given X

Let's start with the assumptions that we stated previously in the introduction to this lesson. That is, let's assume that:

The continuous random variable \(Y\) follows a normal distribution for each \(x\).
The conditional mean of \(Y\) given \(x\), that is, \(E(Y|x)\), is linear in \(x\). Recall that that means, based on our work in the previous lesson, that:

\(E(Y|x)=\mu_Y+\rho \dfrac{\sigma_Y}{\sigma_X}(x-\mu_X)\)
The conditional variance of \(Y\) given \(x\), that is, \(\text{Var}(Y|x)=\sigma^2_{Y|X}\) is constant, that is, the same for each \(x\).

There's a pretty good three-dimensional graph in our textbook depicting these assumptions. A two-dimensional graph with our height and weight example might look something like this:

The blue line represents the linear relationship between x and the conditional mean of \(Y\) given \(x\). For a given height \(x\), say \(x_1\), the red dots are meant to represent possible weights y for that \(x\) value. Note that the range of red dots is intentionally the same for each \(x\) value. That's because we are assuming that the conditional variance \(\sigma^2_{Y|X}\) is the same for each \(x\). If we were to turn this two-dimensional drawing into a three-dimensional drawing, we'd want to draw identical looking normal curves over the top of each set of red dots.

So, in summary, our assumptions tell us so far that the conditional distribution of \(Y\) given \(X=x\) is:

\(Y|x \sim N \left(\mu_Y+\rho \dfrac{\sigma_Y}{\sigma_X}(x-\mu_X),\qquad ??\right)\)

If we could just fill in those question marks, that is, find \(\sigma^2_{Y|X}\), the conditional variance of \(Y\) given \(x\), then we could use what we already know about the normal distribution to find conditional probabilities, such as \(P(140<Y<160|X=x)\). The following theorem does the trick for us.

Theorem

If the conditional distribution of \(Y\) given \(X=x\) follows a normal distribution with mean \(\mu_Y+\rho \dfrac{\sigma_Y}{\sigma_X}(x-\mu_X)\) and constant variance \(\sigma^2_{Y|X}\), then the conditional variance is:

\(\sigma^2_{Y|X}=\sigma^2_Y(1-\rho^2)\)

Proof

Because \(Y\) is a continuous random variable, we need to use the definition of the conditional variance of \(Y\) given \(X=x\) for continuous random variables. That is:

\(\sigma^2_{Y|X}=Var(Y|x)=\int_{-\infty}^\infty (y-\mu_{Y|X})^2 h(y|x) dy\)

Now, if we replace the \(\mu_{Y|X}\) in the integrand with what we know it to be, that is, \(E(Y|x)=\mu_Y+\rho \dfrac{\sigma_Y}{\sigma_X}(x-\mu_X)\), we get:

\(\sigma^2_{Y|X}=\int_{-\infty}^\infty \left[y-\mu_Y-\rho \dfrac{\sigma_Y}{\sigma_X}(x-\mu_X)\right]^2 h(y|x) dy\)

Then, multiplying both sides of the equation by \(f_X(x)\) and integrating over range of \(x\), we get:

\(\int_{-\infty}^\infty \sigma^2_{Y|X} f_X(x)dx=\int_{-\infty}^\infty \int_{-\infty}^\infty \left[y-\mu_Y-\rho \dfrac{\sigma_Y}{\sigma_X}(x-\mu_X)\right]^2 h(y|x) f_X(x)dydx\)

Now, on the left side of the equation, since \(\sigma^2_{Y|X}\) is a constant that doesn't depend on \(x\), we we can pull it through the integral. And, you might recognize that the right side of the equation is an (unconditional) expectation, because:

After pulling the conditional variance through the integral on the left side of the equation, and rewriting the right side of the equation as an expectation, we have:

\(\sigma^2_{Y|X}\int_{-\infty}^\infty f_X(x)dx=E\left\{\left[(Y-\mu_Y)-\left(\rho \dfrac{\sigma_Y}{\sigma_X}(x-\mu_X)\right)\right]^2\right\}\)

Now, by the definition of a valid p.d.f., the integral on the left side of the equation equals 1:

And, dealing with the expectation on the right hand side, that is, squaring the term and distributing the expectation, we get:

\(\sigma^2_{Y|X}=E[(Y-\mu_Y)^2]-2\rho \dfrac{\sigma_Y}{\sigma_X}E[(X-\mu_X)(Y-\mu_Y)]+\rho^2\dfrac{\sigma^2_Y}{\sigma^2_X}E[(X-\mu_X)^2]\)

Now, it's just a matter of recognizing various terms on the right-hand side of the equation:

That is:

\(\sigma^2_{Y|X}= \sigma^2_Y-2\rho \dfrac{\sigma_Y}{\sigma_X} \rho \sigma_X \sigma_Y +\rho^2\dfrac{\sigma^2_Y}{\sigma^2_X}\sigma^2_X\)

Simplifying yet more, we get:

\(\sigma^2_{Y|X}= \sigma^2_Y-2\rho^2\sigma^2_Y+\rho^2\sigma^2_Y=\sigma^2_Y-\rho^2\sigma^2_Y\)

And, finally, we get:

\(\sigma^2_{Y|X}= \sigma^2_Y(1-\rho^2)\)

as was to be proved!

So, in summary, our assumptions tell us that the conditional distribution of \(Y\) given \(X=x\) is:

\(Y|X=x\sim N\left(\mu_Y+\rho \dfrac{\sigma_Y}{\sigma_X}(X-\mu_X),\quad \sigma^2_Y(1-\rho^2)\right)\)

Now that we have completely defined the conditional distribution of \(Y\) given \(X=x\), we can now use what we already know about the normal distribution to find conditional probabilities, such as \(P(140<Y<160|X=x)\). Let's take a look at an example.

Example 21-1

Let \(X\) denote the math score on the ACT college entrance exam of a randomly selected student. Let \(Y\) denote the verbal score on the ACT college entrance exam of a randomly selected student. Previous history suggests that:

\(X\) is normally distributed with a mean of 22.7 and a variance of 17.64
\(Y\) is normally distributed with a mean of 22.7 and variance of 12.25
The correlation between \(X\) and \(Y\) is 0.78.

What is the probability that a randomly selected student's verbal ACT score is between 18.5 and 25.5 points?

Solution

Because \(Y\), the verbal ACT score, is assumed to be normally distributed with a mean of 22.7 and a variance of 12.25, calculating the requested probability involves just making a simple normal probability calculation:

Now converting the \(Y\) scores to standard normal \(Z\) scores, we get:

\(P(18.5<Y<25.5)=P\left(\dfrac{18.5-22.7}{\sqrt{12.25}} <Z<\dfrac{25.5-22.7}{\sqrt{12.25}}\right)\)

And, simplifying and looking up the probabilities in the standard normal table in the back of your textbook, we get:

\begin{align} P(18.5<Y<25.5) &= P(-1.20<Z<0.80)\\ &= 0.7881-0.1151=0.6730 \end{align}

That is, the probability that a randomly selected student's verbal ACT score is between 18.5 and 25.5 points is 0.673.

Now, what happens to our probability calculation if we taken into account the student's ACT math score? That is, what is the probability that a randomly selected student's verbal ACT score is between 18.5 and 25.5 given that his or her ACT math score was 23? That is, what is \(P(18.5<Y<25.5|X=23)\)?

Solution

Before we can do the probability calculation, we first need to fully define the conditional distribution of \(Y\) given \(X=x\):

Now, if we just plug in the values that we know, we can calculate the conditional mean of \(Y\) given \(X=23\):

\(\mu_{Y|23}=22.7+0.78\left(\dfrac{\sqrt{12.25}}{\sqrt{17.64}}\right)(23-22.7)=22.895\)

and the conditional variance of \(Y\) given \(X=x\):

\(\sigma^2_{Y|X}= \sigma^2_Y(1-\rho^2)=12.25(1-0.78^2)=4.7971\)

It is worth noting that \(\sigma^2_{Y|X}\), the conditional variance of \(Y\) given \(X=x\), is much smaller than \(\sigma^2_Y\), the unconditional variance of \(Y\) (12.25). This should make sense, as we have more information about the student. That is, we should expect the verbal ACT scores of all students to span a greater range than the verbal ACT scores of just those students whose math ACT score was 23.

Now, given that a student's math ACT score is 23, we now know that the student's verbal ACT score, \(Y\), is normally distributed with a mean of 22.895 and a variance of 4.7971. Now, calculating the requested probability again involves just making a simple normal probability calculation:

Converting the \(Y\) scores to standard normal \(Z\) scores, we get:

\(P(18.5<Y<25.5|X=23)=P\left(\dfrac{18.5-22.895}{\sqrt{4.7971}} <Z<\dfrac{25.5-22.895}{\sqrt{4.7971}}\right)\)

And, simplifying and looking up the probabilities in the standard normal table in the back of your textbook, we get:

\(P(18.5<Y<25.5|X=23)=P(-2.01<Z<1.19)=0.8830-0.0222=0.8608\)

That is, given that a random selected student's math ACT score is 23, the probability that the student's verbal ACT score is between 18.5 and 25.5 points is 0.8608.

21.2 - Joint P.D.F. of X and Y

We previously assumed that:

\(Y\) follows a normal distribution,
\(E(Y|x)\), the conditional mean of \(Y\) given \(x\) is linear in \(x\), and
\(\text{Var}(Y|x)\), the conditional variance of \(Y\) given \(x\) is constant.

Based on these three stated assumptions, we found the conditional distribution of \(Y\) given \(X=x\). Now, we'll add a fourth assumption, namely that:
\(X\) follows a normal distribution.

Based on the four stated assumptions, we will now define the joint probability density function of \(X\) and \(Y\).

Definition. Assume \(X\) is normal, so that the p.d.f. of \(X\) is:

\(f_X(x)=\dfrac{1}{\sigma_X \sqrt{2\pi}} \text{exp}\left[-\dfrac{(x-\mu_X)^2}{2\sigma^2_X}\right]\)

for \(-\infty<x<\infty\). And, assume that the conditional distribution of \(Y\) given \(X=x\) is normal with conditional mean:

\(E(Y|x)=\mu_Y+\rho \dfrac{\sigma_Y}{\sigma_X}(x-\mu_X)\)

and conditional variance:

\(\sigma^2_{Y|X}= \sigma^2_Y(1-\rho^2)\)

That is, the conditional distribution of \(Y\) given \(X=x\) is:

\begin{align} h(y|x) &= \dfrac{1}{\sigma_{Y|X} \sqrt{2\pi}} \text{exp}\left[-\dfrac{(Y-\mu_{Y|X})^2}{2\sigma^2_{Y|X}}\right]\\ &= \dfrac{1}{\sigma_Y \sqrt{1-\rho^2} \sqrt{2\pi}}\text{exp}\left[-\dfrac{[y-\mu_Y-\rho \dfrac{\sigma_Y}{\sigma_X}(X-\mu_X)]^2}{2\sigma^2_Y(1-\rho^2)}\right],\quad -\infty<x<\infty\\ \end{align}

Therefore, the joint probability density function of \(X\) and \(Y\) is:

\(f(x,y)=f_X(x) \cdot h(y|x)=\dfrac{1}{2\pi \sigma_X \sigma_Y \sqrt{1-\rho^2}} \text{exp}\left[-\dfrac{q(x,y)}{2}\right]\)

where:

\(q(x,y)=\left(\dfrac{1}{1-\rho^2}\right) \left[\left(\dfrac{X-\mu_X}{\sigma_X}\right)^2-2\rho \left(\dfrac{X-\mu_X}{\sigma_X}\right) \left(\dfrac{Y-\mu_Y}{\sigma_Y}\right)+\left(\dfrac{Y-\mu_Y}{\sigma_Y}\right)^2\right]\)

This joint p.d.f. is called the bivariate normal distribution.

Our textbook has a nice three-dimensional graph of a bivariate normal distribution. You might want to take a look at it to get a feel for the shape of the distribution. Now, let's turn our attention to an important property of the correlation coefficient if \(X\) and \(Y\) have a bivariate normal distribution.

Theorem

If \(X\) and \(Y\) have a bivariate normal distribution with correlation coefficient \(\rho_{XY}\), then \(X\) and \(Y\) are independent if and only if \(\rho_{XY}=0\). That "if and only if" means:

If \(X\) and \(Y\) are independent, then \(\rho_{XY}=0\)
If \(\rho_{XY}=0\), then \(X\) and \(Y\) are independent

Recall that the first item is always true. We proved it back in the lesson that addresses the correlation coefficient. We also looked at a counterexample i that lesson that illustrated that item (2) was not necessarily true! Well, now we've just learned a situation in which it is true, that is, when \(X\) and \(Y\) have a bivariate normal distribution. Let's see why item (2) must be true in that case.

Proof

Since we previously proved item (1), our focus here will be in proving item (2). In order to prove that \(X\) and \(Y\) are independent when \(X\) and \(Y\) have the bivariate normal distribution and with zero correlation, we need to show that the bivariate normal density function:

\(f(x,y)=f_X(x)\cdot h(y|x)=\dfrac{1}{2\pi \sigma_X \sigma_Y \sqrt{1-\rho^2}} \text{exp}\left[-\dfrac{q(x,y)}{2}\right]\)

factors into the normal p.d.f of \(X\) and the normal p.d.f. of \(Y\). Well, when \(\rho_{XY}=0\):

\(q(x,y)=\left(\dfrac{1}{1-0^2}\right) \left[\left(\dfrac{X-\mu_X}{\sigma_X}\right)^2+0+\left(\dfrac{Y-\mu_Y}{\sigma_Y}\right)^2 \right]\)

which simplifies to:

\(q(x,y)=\left(\dfrac{X-\mu_X}{\sigma_X}\right)^2+\left(\dfrac{Y-\mu_Y}{\sigma_Y}\right)^2 \)

Substituting this simplified \(q(x,y)\) into the joint p.d.f. of \(X\) and \(Y\), and simplifying, we see that \(f(x,y)\) does indeed factor into the product of \(f(x)\) and \(f(y)\):

\begin{align} f(x,y) &= \dfrac{1}{2\pi \sigma_X \sigma_Y \sqrt{1-\rho^2}} \text{exp}\left[-\dfrac{1}{2}\left(\dfrac{X-\mu_X}{\sigma_X}\right)^2--\dfrac{1}{2}\left(\dfrac{Y-\mu_Y}{\sigma_Y}\right)^2\right]\\ &= \dfrac{1}{\sigma_X \sqrt{2\pi} \sigma_Y \sqrt{2\pi}}\text{exp}\left[-\dfrac{(x-\mu_X)^2}{2\sigma_X^2}\right] \text{exp}\left[-\dfrac{(y-\mu_Y)^2}{2\sigma_Y^2}\right]\\ &= \dfrac{1}{\sigma_X \sqrt{2\pi}}\text{exp}\left[-\dfrac{(x-\mu_X)^2}{2\sigma_X^2}\right]\cdot \dfrac{1}{\sigma_Y \sqrt{2\pi}}\text{exp}\left[-\dfrac{(y-\mu_Y)^2}{2\sigma_Y^2}\right]\\ &=f_X(x)\cdot f_Y(y)\\ \end{align}

Because we have shown that:

\(f(x,y)=f_X(x)\cdot f_Y(y)\)

we can conclude, by the definition of independence, that \(X\) and \(Y\) are independent. Our proof is complete.

^[1]	Link
↥	Has Tooltip/Popover
	Toggleable Visibility

Section 4: Bivariate Distributions

Lesson 17: Distributions of Two Discrete Random Variables

Overview

Objectives

17.1 - Two Discrete Random Variables

Example 17-1

Solution

Example 17-1 (continued)

Solution

Example 17-1 (continued again)

Solution

17.2 - A Triangular Support

Example 17-2

Solution

17.3 - The Trinomial Distribution

Example 17-3

Solution

Example 17-3 continued

Solution

Lesson 18: The Correlation Coefficient

Overview

18.1 - Covariance of X and Y

Example 18-1

Solution

Proof

Example 18.1 continued

Solution

18.2 - Correlation Coefficient of X and Y

Example 18-1 (continued)

Interpretation of Correlation

18.3 - Understanding Rho

Proof

Example 18-2

Solution

Example 18-3

Solution

Example 18-4

Solution

18.4 - More on Understanding Rho

Question #1

Questions #2, #3, #4

Solution

Solution

Lesson 19: Conditional Distributions

Overview

Objectives

19.1 - What is a Conditional Distribution?

Example 19-1

Example (continued)

Solution

Example (continued)

Solution

Example (continued)

Solution

19.2 - Definitions

Example 19-2

Solution

Solution

19.3 - Conditional Means and Variances

Example 19-3

Solution

Solution

Solution

Lesson 20: Distributions of Two Continuous Random Variables

Overview

Objectives

20.1 - Two Continuous Random Variables

Example 20-1

Solution

Solution

Example (continued)

Solution

Example (continued)

Solution

Example (continued)

Solution

Example 20-2

Solution

20.2 - Conditional Distributions for Continuous Random Variables

Example 20-3