Lesson 17: Distributions of Two Discrete Random Variables
Lesson 17: Distributions of Two Discrete Random VariablesOverview
As the title of the lesson suggests, in this lesson, we'll learn how to extend the concept of a probability distribution of one random variable \(X\) to a joint probability distribution of two random variables \(X\) and \(Y\). In some cases, \(X\) and \(Y\)may both be discrete random variables. For example, suppose \(X\) denotes the number of significant others a randomly selected person has, and \(Y\) denotes the number of arguments the person has each week. We might want to know if there is a relationship between \(X\) and \(Y\). Or, we might want to know the probability that \(X\) takes on a particular value \(x\) and \(Y\) takes on a particular value \(y\). That is, we might want to know \(P(X=x, Y=y)\).
Objectives
- To learn the formal definition of a joint probability mass function of two discrete random variables.
- To learn how to use a joint probability mass function to find the probability of a specific event.
- To learn how to find a marginal probability mass function of a discrete random variable \(X\) from the joint probability mass function of \(X\) and \(Y\).
- To learn a formal definition of the independence of two random variables \(X\) and \(Y\).
- To learn how to find the expectation of a function of the discrete random variables \(X\) and \(Y\) using their joint probability mass function.
- To learn how to find the means and variances of the discrete random variables \(X\) and \(Y\) using their joint probability mass function.
- To learn what it means that \(X\) and \(Y\) have a joint triangular support.
- To learn that, in general, any two random variables \(X\) and \(Y\) having a joint triangular support must be dependent.
- To learn what it means that \(X\) and \(Y\) have a joint rectangular support.
- To learn that, in general, any two random variables \(X\) and \(Y\) having a joint rectangular support may or may not be independent.
- To learn about the trinomial distribution.
- To be able to apply the methods learned in the lesson to new problems.
17.1 - Two Discrete Random Variables
17.1 - Two Discrete Random VariablesLet's start by first considering the case in which the two random variables under consideration, \(X\) and \(Y\), say, are both discrete. We'll jump in right in and start with an example, from which we will merely extend many of the definitions we've learned for one discrete random variable, such as the probability mass function, mean and variance, to the case in which we have two discrete random variables.
Example 17-1

Suppose we toss a pair of fair, four-sided dice, in which one of the dice is RED and the other is BLACK. We'll let:
- \(X\) = the outcome on the RED die = \(\{1, 2, 3, 4\}\)
- \(Y\) = the outcome on the BLACK die = \(\{1, 2, 3, 4\}\)
What is the probability that \(X\) takes on a particular value \(x\), and \(Y\) takes on a particular value \(y\)? That is, what is \(P(X=x, Y=y)\)?
Solution
Just as we have to in the case with one discrete random variable, in order to find the "joint probability distribution" of \(X\) and \(Y\), we first need to define the support of \(X\) and \(Y\). Well, the support of \(X\) is:
\(S_1=\{1, 2, 3, 4\}\)
And, the support of \(Y\) is:
\(S_2=\{1, 2, 3, 4\}\)
Now, if we let \((x,y)\) denote one of the possible outcomes of one toss of the pair of dice, then certainly (1, 1) is a possible outcome, as is (1, 2), (1, 3) and (1, 4). If we continue to enumerate all of the possible outcomes, we soon see that the joint support S has 16 possible outcomes:
\(S=\{(1,1), (1,2), (1,3), (1,4), (2,1), (2,2), (2,3), (2,4), (3,1), (3,2), (3,3), (3,4), (4,1), (4,2), (4,3), (4,4)\}\)
Now, because the dice are fair, we should expect each of the 16 possible outcomes to be equally likely. Therefore, using the classical approach to assigning probability, the probability that \(X\) equals any particular \(x\) value, and \(Y\) equals any particular \(y\) value, is \(\frac{1}{16}\). That is, for all \((x,y)\) in the support \(S\):
\(P(X=x, Y=y)=\frac{1}{16}\)
Because we have identified the probability for each \((x, y)\), we have found what we call the joint probability mass function. Perhaps, it is not too surprising that the joint probability mass function, which is typically denoted as \(f(x,y)\), can be defined as a formula (as we have above), as a graph, or as a table. Here's what our joint p.m.f. would like in tabular form:
Now that we've found our first joint probability mass function, let's formally define it now.
- Joint Probability Mass Function
- Let \(X\) and \(Y\) be two discrete random variables, and let \(S\) denote the two-dimensional support of \(X\) and \(Y\). Then, the function \(f(x,y)=P(X=x, Y=y)\) is a joint probability mass function (abbreviated p.m.f.) if it satisfies the following three conditions:
-
\(0 \leq f(x,y) \leq 1\)
-
\(\mathop{\sum\sum}\limits_{(x,y)\in S} f(x,y)=1\)
-
\(P[(X,Y) \in A]=\mathop{\sum\sum}\limits_{(x,y)\in A} f(x,y)\) where \(A\) is a subset of the support \(S\).
The first condition, of course, just tells us that each probability must be a valid probability number between 0 and 1 (inclusive). The second condition tells us that, just as must be true for a p.m.f. of one discrete random variable, the sum of the probabilities over the entire support \(S\) must equal 1. The third condition tells us that in order to determine the probability of an event \(A\), you simply sum up the probabilities of the \((x,y)\) values in \(A\).
Now, if you take a look back at the representation of our joint p.m.f. in tabular form, you can see that the last column contains the probability mass function of \(X\) alone, and the last row contains the probability mass function of \(Y\) alone. Those two functions, \(f(x)\) and \(f(y)\), which in this setting are typically referred to as marginal probability mass functions, are obtained by simply summing the probabilities over the support of the other variable. That is, to find the probability mass function of \(X\), we sum, for each \(x\), the probabilities when \(y=1, 2, 3, \text{ and } 4\). That is, for each \(x\), we sum \(f(x, 1), f(x, 2), f(x, 3), \text{ and }f(x, 4)\). Now that we've seen the two marginal probability mass functions in our example, let's give a formal definition of a marginal probability mass function.
- Marginal Probability Mass Function of \(X\)
-
Let \(X\) be a discrete random variable with support \(S_1\), and let \(Y\) be a discrete random variable with support \(S_2\). Let \(X\) and \(Y\) have the joint probability mass function \(f(x, y)\) with support \(S\). Then, the probability mass function of \(X\) alone, which is called the marginal probability mass function of \(X\), is defined by:
\(f_X(x)=\sum\limits_y f(x,y)=P(X=x),\qquad x\in S_1\)
where, for each \(x\) in the support \(S_1\), the summation is taken over all possible values of \(y\). Similarly, the probability mass function of \(Y\) alone, which is called the marginal probability mass function of \(Y\), is defined by:
\(f_Y(y)=\sum\limits_x f(x,y)=P(Y=y),\qquad y\in S_2\)
where, for each \(y\) in the support \(S_2\), the summation is taken over all possible values of \(x\).
If you again take a look back at the representation of our joint p.m.f. in tabular form, you might notice that the following holds true:
\(P(X=x,Y=y)=\dfrac{1}{16}=P(X=x)\cdot P(Y=y)=\dfrac{1}{4} \cdot \dfrac{1}{4}=\dfrac{1}{16}\)
for all \(x\in S_1, y\in S_2\). When this happens, we say that \(X\) and \(Y\) are independent. A formal definition of the independence of two random variables \(X\) and \(Y\) follows.
- Independent and Dependent Random Variables
-
The random variables \(X\) and \(Y\) are independent if and only if:
\(P(X=x, Y=y)=P(X=x)\times P(Y=y)\)
for all \(x\in S_1, y\in S_2\). Otherwise, \(X\) and \(Y\) are said to be dependent.
Now, suppose we were given a joint probability mass function \(f(x, y)\), and we wanted to find the mean of \(X\). Well, one strategy would be to find the marginal p.m.f of \(X\) first, and then use the definition of the expected value that we previously learned to calculate \(E(X)\). Alternatively, we could use the following definition of the mean that has been extended to accommodate joint probability mass functions.
Definition. Let \(X\) be a discrete random variable with support \(S_1\), and let \(Y\) be a discrete random variable with support \(S_2\). Let \(X\) and \(Y\) be discrete random variables with joint p.m.f. \(f(x,y)\) on the support \(S\). If \(u(X,Y)\) is a function of these two random variables, then:
\(E[u(X,Y)]=\mathop{\sum\sum}\limits_{(x,y)\in S} u(x,y)f(x,y)\)
if it exists, is called the expected value of \(u(X,Y)\). If \(u(X,Y)=X\), then:
\(\mu_X=E[X]=\sum\limits_{x\in S_1} \sum\limits_{y\in S_2} xf(x,y)\)
if it exists, is the mean of \(X\). If \(u(X,Y)=Y\), then:
\(\mu_Y=E[Y]=\sum\limits_{x\in S_1} \sum\limits_{y\in S_2} yf(x,y)\)
if it exists, is the mean of \(Y\).
Example 17-1 (continued)
Consider again our example in which we toss a pair of fair, four-sided dice, in which one of the dice is RED and the other is BLACK. Again, letting:
- \(X\) = the outcome on the RED die = \(\{1, 2, 3, 4\}\)
- \(Y\) = the outcome on the BLACK die = \(\{1, 2, 3, 4\}\)
What is the mean of \(X\) ? And, what is the mean of \(Y\)?
Solution
The mean of \(X\) is calculated as:
\(\mu_X=E[X]=\sum\limits_{x\in S_1} \sum\limits_{y\in S_2} xf(x,y) =1\left(\dfrac{1}{16}\right)+\cdots+1\left(\dfrac{1}{16}\right)+\cdots+4\left(\dfrac{1}{16}\right)+\cdots+4\left(\dfrac{1}{16}\right)\)
which simplifies to:
\(\mu_X=E[X]=1\left(\dfrac{4}{16}\right)+2\left(\dfrac{4}{16}\right)+3\left(\dfrac{4}{16}\right)+4\left(\dfrac{4}{16}\right)=\dfrac{40}{16}=2.5\)
The mean of \(Y\) is similarly calculated as:
\(\mu_Y=E[Y]=\sum\limits_{x\in S_1} \sum\limits_{y\in S_2} yf(x,y)=1\left(\dfrac{1}{16}\right)+\cdots+1\left(\dfrac{1}{16}\right)+\cdots+4\left(\dfrac{1}{16}\right)+\cdots+4\left(\dfrac{1}{16}\right)\)
which simplifies to:
\(\mu_Y=E[Y]=1\left(\dfrac{4}{16}\right)+2\left(\dfrac{4}{16}\right)+3\left(\dfrac{4}{16}\right)+4\left(\dfrac{4}{16}\right)=\dfrac{40}{16}=2.5\)
By the way, you probably shouldn't find it surprising that the formula for the mean of \(X\) reduces to:
\(\mu_X=\sum\limits_{x\in S_1} xf(x)\)
because:
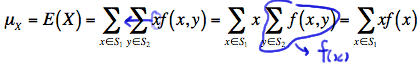
That is, the third equality holds because the x values don't depend on \(y\) and therefore can be pulled through the summation over \(y\). And, the last equality holds because of the definition of the marginal probability mass function of \(X\). Similarly, the mean of \(Y\) reduces to:
\(\mu_Y=\sum\limits_{y\in S_2} yf(y)\)
because:
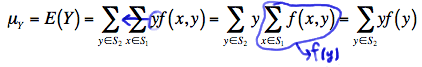
That is, again, the third equality holds because the y values don't depend on \(x\) and therefore can be pulled through the summation over \(x\). And, the last equality holds because of the definition of the marginal probability mass function of \(Y\).
Now, suppose we were given a joint probability mass function \(f(x,y)\), and we wanted to find the variance of \(X\). Again, one strategy would be to find the marginal p.m.f of \(X\) first, and then use the definition of the expected value that we previously learned to calculate \(\text{Var}(X)\). Alternatively, we could use the following definition of the variance that has been extended to accommodate joint probability mass functions.
Definition. Let \(X\) be a discrete random variable with support \(S_1\), and let \(Y\) be a discrete random variable with support \(S_2\). Let \(X\) and \(Y\) be discrete random variables with joint p.m.f. \(f(x,y)\) on the support \(S\). If \(u(X,Y)\) is a function of these two random variables, then:
\(E[u(X,Y)]=\mathop{\sum\sum}\limits_{(x,y)\in S} u(x,y)f(x,y)\)
if it exists, is called the expected value of \(u(X,Y)\). If \(u(X,Y)=(X-\mu_X)^2\), then:
\(\sigma^2_X=Var[X]=\sum\limits_{x\in S_1} \sum\limits_{y\in S_2} (x-\mu_X)^2 f(x,y)\)
if it exists, is the variance of \(X\). The variance of \(X\) can also be calculated using the shortcut formula:
\(\sigma^2_X=E(X^2)-\mu^2_X=\left(\sum\limits_{x\in S_1} \sum\limits_{y\in S_2} x^2 f(x,y)\right)-\mu^2_X\)
If \(u(X,Y)=(Y-\mu_Y)^2\), then:
\(\sigma^2_Y=Var[Y]=\sum\limits_{x\in S_1} \sum\limits_{y\in S_2} (y-\mu_Y)^2 f(x,y)\)
if it exists, is the variance of \(Y\). The variance of \(Y\) can also be calculated using the shortcut formula:
\(\sigma^2_Y=E(Y^2)-\mu^2_Y=\left(\sum\limits_{x\in S_1} \sum\limits_{y\in S_2} y^2 f(x,y)\right)-\mu^2_Y\)
Example 17-1 (continued again)
Consider yet again our example in which we toss a pair of fair, four-sided dice, in which one of the dice is RED and the other is BLACK. Again, letting:
- \(X\) = the outcome on the RED die = \(\{1, 2, 3, 4\}\)
- \(Y\) = the outcome on the BLACK die = \(\{1, 2, 3, 4\}\)
What is the variance of \(X\) ? And, what is the variance of \(Y\)?
Solution
Using the definition, the variance of \(X\) is calculated as:
\(\sigma^2_X=\sum\limits_{x\in S_1} \sum\limits_{y\in S_2} (x-\mu_X)^2 f(x,y)=(1-2.5)^2\left(\dfrac{1}{16}\right)+\cdots+(4-2.5)^2\left(\dfrac{1}{16}\right)=1.25\)
Thankfully, we get the same answer using the shortcut formula for the variance of \(X\):
\(\sigma^2_X=E(X^2)-\mu^2_X=\left(\sum\limits_{x\in S_1} \sum\limits_{y\in S_2} x^2 f(x,y)\right)-\mu^2_X=\left[1^2 \left(\dfrac{1}{16}\right)+\cdots+4^2 \left(\dfrac{1}{16}\right)\right]-2.5^2=\dfrac{120}{16}-6.25=1.25\)
Calculating the variance of \(Y\) is left for you as an exercise. You should, because of the symmetry, also get \(\text{Var}(Y)=1.25\).
17.2 - A Triangular Support
17.2 - A Triangular SupportWe now have many of the gory definitions behind us. One of the definitions we learned in particular is that two random variables \(X\) and \(Y\) are independent if and only if:
\(P(X=x, Y=x)=P(X=x)\times P(Y=y)\)
for all \(x\in S_1, y\in S_2\). Otherwise, \(X\) and \(Y\) are said to be dependent. On the previous page, our example comprised two random variables \(X\) and \(Y\), which were deemed to be independent. On this page, we'll explore, by way of another example, two random variables \(X\) and \(Y\), which are deemed to be dependent.
Example 17-2
Consider the following joint probability mass function:
\(f(x,y)=\dfrac{xy^2}{13}\)
in which the support is \(S=\{(x, y)\}=\{(1, 1), (1, 2), (2,2)\}\). Are the random variables \(X\) and \(Y\) independent?
Solution
We are given the joint probability mass function as a formula. We can therefore easily calculate the joint probabilities for each \((x, y)\) in the support \(S\):
when \(x=1\) and \(y=1\): \(f(1,1)=\dfrac{(1)(1)^2}{13}=\dfrac{1}{13}\)
when \(x=1\) and \(y=2\): \(f(1,2)=\dfrac{(1)(2)^2}{13}=\dfrac{4}{13}\)
when \(x=2\) and \(y=2\): \(f(2,2)=\dfrac{(2)(2)^2}{13}=\dfrac{8}{13}\)
Now that we have calculated each of the joint probabilities, we can alternatively present the p.m.f. in tabular form, complete with the marginal p.m.f.s of \(X\) and \(Y\), as:
As an aside, you should note that the joint support \(S\) of \(X\) and \(Y\) is what we call a "triangular support," because, well, it's shaped like a triangle:
Anyway, perhaps it is easy now to see that \(X\) and \(Y\) are dependent, because, for example:
\(f(1,2)=\dfrac{4}{13} \neq f_X(1)\cdot f_Y(2)=\dfrac{5}{13} \times \dfrac{12}{13}\)
Note though that, in general, any two random variables \(X\) and \(Y\) having a joint triangular support must be dependent because you can always find:
\(f(x)\times f(y)=c\ne0\)
for some non-zero constant \(c\). For example, for the joint p.m.f. above:
\(f_X(2)\times f_Y(1)=\left(\frac{8}{13}\right)\times\left(\frac{1}{13}\right)=\frac{8}{169}\ne 0=f_{X,Y}(2,1)\)
In general, random variables with rectangular support may or may not be independent.
17.3 - The Trinomial Distribution
17.3 - The Trinomial DistributionYou might recall that the binomial distribution describes the behavior of a discrete random variable \(X\), where \(X\) is the number of successes in \(n\) tries when each try results in one of only two possible outcomes. What happens if there aren't two, but rather three, possible outcomes? That's what we'll explore here on this page, ending up not with the binomial distribution, but rather the trinomial distribution. A rather fitting name, I might say!
Example 17-3

Suppose \(n=20\) students are selected at random:
- Let \(A\) be the event that a randomly selected student went to the football game on Saturday. Also, let \(P(A)=0.20=p_1\), say.
- Let \(B\) be the event that a randomly selected student watched the football game on TV on Saturday. Let \(P(B)=0.50=p_2\), say.
- Let \(C\) be the event that a randomly selected student completely ignored the football game on Saturday. Let \(P(C)=0.3=1-p_1-p_2\).
One possible outcome, then, of selecting the 20 students at random is:
BBCABBAACABBBCCBCBCB
That is, the first two students watched the game on TV, the third student ignored the game, the fourth student went to the game, and so on. Now, if we let \(X\)denote the number in the sample who went to the football game on Saturday, let \(Y\) denote the number in the sample who watched the football game on TV on Saturday, and let \(Z\) denote the number in the sample who completely ignored the football game, then in this case:
- \(X=4\) (because there are 4 As)
- \(Y=10\) (because there are 10 Bs)
- \(Z=20-X-Y\) (and yes, indeed, there are 6 Cs)
What is the joint probability mass function of \(X\)and \(Y\)?
Solution
This example lends itself to the following formal definition.
Definition. Suppose we repeat an experiment \(n\) independent times, with each experiment ending in one of three mutually exclusive and exhaustive ways (success, first kind of failure, second kind of failure). If we let \(X\) denote the number of times the experiment results in a success, let \(Y\) denote the number of times the experiment results in a failure of the first kind, and let \(Z\) denote the number of times the experiment results in a failure of the second kind, then the joint probability mass function of \(X\) and \(Y\) is:
\(f(x,y)=P(X=x,Y=y)=\dfrac{n!}{x!y!(n-x-y)!} p^x_1 p^y_2 (1-p_1-p_2)^{n-x-y}\)
with:
\(x=0, 1, \ldots, n\)
\(y=0, 1, \ldots, n\)
\(x+y\le n\)
Example 17-3 continued
What are the marginal probability mass functions of \(X\)and \(Y\)? Are \(X\)and \(Y\) independent? or dependent?
Solution
We can easily just lump the two kinds of failures back together, thereby getting that \(X\), the number of successes, is a binomial random variable with parameters \(n\) and \(p_1\). That is:
\(f(x)=\dfrac{n!}{x!(n-x)!} p^x_1 (1-p_1)^{n-x}\)
with \(x=0, 1, \ldots, n\). Similarly, we can lump the successes in with the failures of the second kind, thereby getting that \(Y\), the number of failures of the first kind, is a binomial random variable with parameters \(n\) and \(p_2\). That is:
\(f(y)=\dfrac{n!}{y!(n-y)!} p^y_2 (1-p_2)^{n-y}\)
with \(y=0, 1, \ldots, n\). Therefore, \(X\) and \(Y\) must be dependent, because if we multiply the p.m.f.s of \(X\) and \(Y\) together, we don't get the trinomial p.m.f. That is, \(f(x,y)\ne f(x)\times f(y)\):
\(\left[\dfrac{n!}{x!y!(n-x-y)!} p^x_1 p^y_2 (1-p_1-p_2)^{n-x-y}\right] \neq \left[\dfrac{n!}{x!(n-x)!} p^x_1 (1-p_1)^{n-x}\right] \times \left[\dfrac{n!}{y!(n-y)!} p^y_2 (1-p_2)^{n-y}\right]\)
By the way, there's also another way of arguing that \(X\) and \(Y\) must be dependent... because the joint support of \(X\) and \(Y\) is triangular!