Section 5: Distributions of Functions of Random Variables

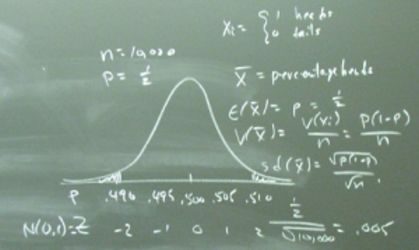
As the name of this section suggests, we will now spend some time learning how to find the probability distribution of functions of random variables. For example, we might know the probability density function of $X$ , but want to know instead the probability density function of $u (X) = X^{2}$ . We'll learn several different techniques for finding the distribution of functions of random variables, including the distribution function technique, the change-of-variable technique and the moment-generating function technique.

The more important functions of random variables that we'll explore will be those involving random variables that are independent and identically distributed. For example, if $X_{1}$ is the weight of a randomly selected individual from the population of males, $X_{2}$ is the weight of another randomly selected individual from the population of males, ..., and $X_{n}$ is the weight of yet another randomly selected individual from the population of males, then we might be interested in learning how the random function:

$\bar{X} = \frac{X_{1} + X_{2} + \dots + X_{n}}{n}$

is distributed. We'll first learn how $\bar{X}$ is distributed assuming that the $X_{i}$ 's are normally distributed. Then, we'll strip away the assumption of normality, and use a classic theorem, called the Central Limit Theorem, to show that, for large $n$ , the function:

$\frac{\sqrt{n} (\bar{X} - μ)}{σ}$

approximately follows the standard normal distribution. Finally, we'll use the Central Limit Theorem to use the normal distribution to approximate discrete distributions, such as the binomial distribution and the Poisson distribution.

Lesson 22: Functions of One Random Variable

Overview

We'll begin our exploration of the distributions of functions of random variables, by focusing on simple functions of one random variable. For example, if $X$ is a continuous random variable, and we take a function of $X$ , say:

$Y = u (X)$

then $Y$ is also a continuous random variable that has its own probability distribution. We'll learn how to find the probability density function of $Y$ , using two different techniques, namely the distribution function technique and the change-of-variable technique. At first, we'll focus only on one-to-one functions. Then, once we have that mastered, we'll learn how to modify the change-of-variable technique to find the probability of a random variable that is derived from a two-to-one function. Finally, we'll learn how the inverse of a cumulative distribution function can help us simulate random numbers that follow a particular probability distribution.

Objectives

Upon completion of this lesson, you should be able to:

To learn how to use the distribution function technique to find the probability distribution of $Y = u (X)$ , a one-to-one transformation of a random variable $X$ .
To learn how to use the change-of-variable technique to find the probability distribution of $Y = u (X)$ , a one-to-one transformation of a random variable $X$ .
To learn how to use the change-of-variable technique to find the probability distribution of $Y = u (X)$ , a two-to-one transformation of a random variable $X$ .
To learn how to use a cumulative distribution function to simulate random numbers that follow a particular probability distribution.
To understand all of the proofs in the lesson.
To be able to apply the methods learned in the lesson to new problems.

22.1 - Distribution Function Technique

You might not have been aware of it at the time, but we have already used the distribution function technique at least twice in this course to find the probability density function of a function of a random variable. For example, we used the distribution function technique to show that:

$Z = \frac{X - μ}{σ}$

follows a standard normal distribution when $X$ is normally distributed with mean $μ$ and standard deviation $σ$ . And, we used the distribution function technique to show that, when $Z$ follows the standard normal distribution:

$Z^{2}$

follows the chi-square distribution with 1 degree of freedom. In summary, we used the distribution function technique to find the p.d.f. of the random function $Y = u (X)$ by:

First, finding the cumulative distribution function:

$F_{Y} (y) = P (Y \leq y)$
Then, differentiating the cumulative distribution function $F (y)$ to get the probability density function $f (y)$ . That is:

$f_{Y} (y) = F_{Y}^{'} (y)$

Now that we've officially stated the distribution function technique, let's take a look at a few more examples.

Example 22-1

Let $X$ be a continuous random variable with the following probability density function:

$f (x) = 3 x^{2}$

for $0 < x < 1$ . What is the probability density function of $Y = X^{2}$ ?

Solution

If you look at the graph of the function (above and to the right) of $Y = X^{2}$ , you might note that (1) the function is an increasing function of $X$ , and (2) $0 < y < 1$ . That noted, let's now use the distribution function technique to find the p.d.f. of $Y$ . First, we find the cumulative distribution function of $Y$ :

https://www.youtube.com/watch/rNiQ-jfTTEA ^[1]

Having shown that the cumulative distribution function of $Y$ is:

$F_{Y} (y) = y^{3 / 2}$

for $0 < y < 1$ , we now just need to differentiate $F (y)$ to get the probability density function $f (y)$ . Doing so, we get:

$f_{Y} (y) = F_{Y}^{'} (y) = \frac{3}{2} y^{1 / 2}$

for $0 < y < 1$ . Our calculation is complete! We have successfully used the distribution function technique to find the p.d.f of $Y$ , when $Y$ was an increasing function of $X$ . (By the way, you might find it reassuring to verify that $f (y)$ does indeed integrate to 1 over the support of $y$ . In general, that's not a bad thing to check.)

One thing you might note in the last example is that great care was used to subscript the cumulative distribution functions and probability density functions with either an $X$ or a $Y$ to indicate to which random variable the functions belonged. For example, in finding the cumulative distribution function of $Y$ , we started with the cumulative distribution function of $Y$ , and ended up with a cumulative distribution function of $X$ ! If we didn't use the subscripts, we would have had a good chance of throwing up our hands and botching the calculation. In short, using subscripts is a good habit to follow!

Example 22-2

Let $X$ be a continuous random variable with the following probability density function:

$f (x) = 3 (1 - x)^{2}$

for $0 < x < 1$ . What is the probability density function of $Y = (1 - X)^{3}$ ?

Solution

If you look at the graph of the function (above and to the right) of:

$Y = (1 - X)^{3}$

you might note that the function is a decreasing function of $X$ , and $0 < y < 1$ . That noted, let's now use the distribution function technique to find the p.d.f. of $Y$ . First, we find the cumulative distribution function of $Y$ :

https://www.youtube.com/watch/nwkoDujUYMc ^[2]

Having shown that the cumulative distribution function of $Y$ is:

$F_{Y} (y) = y$

for $0 < y < 1$ , we now just need to differentiate $F (y)$ to get the probability density function $f (y)$ . Doing so, we get:

$f_{Y} (y) = F_{Y}^{'} (y) = 1$

for $0 < y < 1$ . That is, $Y$ is a $U (0, 1)$ random variable. (Again, you might find it reassuring to verify that $f (y)$ does indeed integrate to 1 over the support of $y$ .)

22.2 - Change-of-Variable Technique

On the last page, we used the distribution function technique in two different examples. In the first example, the transformation of $X$ involved an increasing function, while in the second example, the transformation of $X$ involved a decreasing function. On this page, we'll generalize what we did there first for an increasing function and then for a decreasing function. The generalizations lead to what is called the change-of-variable technique.

Generalization for an Increasing Function

Let $X$ be a continuous random variable with a generic p.d.f. $f (x)$ defined over the support $c_{1} < x < c_{2}$ . And, let $Y = u (X)$ be a continuous, increasing function of $X$ with inverse function $X = v (Y)$ . Here's a picture of what the continuous, increasing function might look like:

The blue curve, of course, represents the continuous and increasing function $Y = u (X)$ . If you put an $x$ -value, such as $c_{1}$ and $c_{2}$ , into the function $Y = u (X)$ , you get a $y$ -value, such as $u (c_{1})$ and $u (c_{2})$ . But, because the function is continuous and increasing, an inverse function $X = v (Y)$ exists. In that case, if you put a $y$ -value into the function $X = v (Y)$ , you get an $x$ -value, such as $v (y)$ .

Okay, now that we have described the scenario, let's derive the distribution function of $Y$ . It is:

$F_{Y} (y) = P (Y \leq y) = P (u (X) \leq y) = P (X \leq v (y)) = \int_{c_{1}}^{v (y)} f (x) d x$

for $d_{1} = u (c_{1}) < y < u (c_{2}) = d_{2}$ . The first equality holds from the definition of the cumulative distribution function of $Y$ . The second equality holds because $Y = u (X)$ . The third equality holds because, as shown in red on the following graph, for the portion of the function for which $u (X) \leq y$ , it is also true that $X \leq v (Y)$ :

And, the last equality holds from the definition of probability for a continuous random variable $X$ . Now, we just have to take the derivative of $F_{Y} (y)$ , the cumulative distribution function of $Y$ , to get $f_{Y} (y)$ , the probability density function of $Y$ . The Fundamental Theorem of Calculus, in conjunction with the Chain Rule, tells us that the derivative is:

$f_{Y} (y) = F_{Y}^{'} (y) = f_{x} (v (y)) \cdot v^{'} (y)$

for $d_{1} = u (c_{1}) < y < u (c_{2}) = d_{2}$ .

Generalization for a Decreasing Function

Let $X$ be a continuous random variable with a generic p.d.f. $f (x)$ defined over the support $c_{1} < x < c_{2}$ . And, let $Y = u (X)$ be a continuous, decreasing function of $X$ with inverse function $X = v (Y)$ . Here's a picture of what the continuous, decreasing function might look like:

The blue curve, of course, represents the continuous and decreasing function $Y = u (X)$ . Again, if you put an $x$ -value, such as $c_{1}$ and $c_{2}$ , into the function $Y = u (X)$ , you get a $y$ -value, such as $u (c_{1})$ and $u (c_{2})$ . But, because the function is continuous and decreasing, an inverse function $X = v (Y)$ exists. In that case, if you put a $y$ -value into the function $X = v (Y)$ , you get an x-value, such as $v (y)$ .

That said, the distribution function of $Y$ is then:

$F_{Y} (y) = P (Y \leq y) = P (u (X) \leq y) = P (X \geq v (y)) = 1 - P (X \leq v (y)) = 1 - \int_{c_{1}}^{v (y)} f (x) d x$

for $d_{2} = u (c_{2}) < y < u (c_{1}) = d_{1}$ . The first equality holds from the definition of the cumulative distribution function of $Y$ . The second equality holds because $Y = u (X)$ . The third equality holds because, as shown in red on the following graph, for the portion of the function for which $u (X) \leq y$ , it is also true that $X \geq v (Y)$ :

The fourth equality holds from the rule of complementary events. And, the last equality holds from the definition of probability for a continuous random variable $X$ . Now, we just have to take the derivative of $F_{Y} (y)$ , the cumulative distribution function of $Y$ , to get $f_{Y} (y)$ , the probability density function of $Y$ . Again, the Fundamental Theorem of Calculus, in conjunction with the Chain Rule, tells us that the derivative is:

$f_{Y} (y) = F_{Y}^{'} (y) = - f_{x} (v (y)) \cdot v^{'} (y)$

for $d_{2} = u (c_{2}) < y < u (c_{1}) = d_{1}$ . You might be alarmed in that it seems that the p.d.f. $f (y)$ is negative, but note that the derivative of $v (y)$ is negative, because $X = v (Y)$ is a decreasing function in $Y$ . Therefore, the two negatives cancel each other out, and therefore make $f (y)$ positive.

Phew! We have now derived what is called the change-of-variable technique first for an increasing function and then for a decreasing function. But, continuous, increasing functions and continuous, decreasing functions, by their one-to-one nature, are both invertible functions. Let's, once and for all, then write the change-of-variable technique for any generic invertible function.

Definition. Let $X$ be a continuous random variable with generic probability density function $f (x)$ defined over the support $c_{1} < x < c_{2}$ . And, let $Y = u (X)$ be an invertible function of $X$ with inverse function $X = v (Y)$ . Then, using the change-of-variable technique, the probability density function of $Y$ is:

$f_{Y} (y) = f_{X} (v (y)) \times | v^{'} (y) |$

defined over the support $u (c_{1}) < y < u (c_{2})$ .

Having summarized the change-of-variable technique, once and for all, let's revisit an example.

Example 22-1 Continued

Let's return to our example in which $X$ is a continuous random variable with the following probability density function:

$f (x) = 3 x^{2}$

for $0 < x < 1$ . Use the change-of-variable technique to find the probability density function of $Y = X^{2}$ .

Solution

Note that the function:

$Y = X^{2}$

defined over the interval $0 < x < 1$ is an invertible function. The inverse function is:

$x = v (y) = \sqrt{y} = y^{1 / 2}$

for $0 < y < 1$ . (That range is because, when $x = 0, y = 0$ ; and when $x = 1, y = 1$ ). Now, taking the derivative of $v (y)$ , we get:

$v^{'} (y) = \frac{1}{2} y^{- 1 / 2}$

Therefore, the change-of-variable technique:

$f_{Y} (y) = f_{X} (v (y)) \times | v^{'} (y) |$

tells us that the probability density function of $Y$ is:

$f_{Y} (y) = 3 [y^{1 / 2}]^{2} \cdot \frac{1}{2} y^{- 1 / 2}$

And, simplifying we get that the probability density function of $Y$ is:

$f_{Y} (y) = \frac{3}{2} y^{1 / 2}$

for $0 < y < 1$ . We shouldn't be surprised by this result, as it is the same result that we obtained using the distribution function technique.

Example 22-2 continued

Let's return to our example in which $X$ is a continuous random variable with the following probability density function:

$f (x) = 3 (1 - x)^{2}$

for $0 < x < 1$ . Use the change-of-variable technique to find the probability density function of $Y = (1 - X)^{3}$ .

Solution

Note that the function:

$Y = (1 - X)^{3}$

defined over the interval $0 < x < 1$ is an invertible function. The inverse function is:

$x = v (y) = 1 - y^{1 / 3}$

for $0 < y < 1$ . (That range is because, when $x = 0, y = 1$ ; and when $x = 1, y = 0$ ). Now, taking the derivative of $v (y)$ , we get:

$v^{'} (y) = - \frac{1}{3} y^{- 2 / 3}$

Therefore, the change-of-variable technique:

$f_{Y} (y) = f_{X} (v (y)) \times | v^{'} (y) |$

tells us that the probability density function of $Y$ is:

$f_{Y} (y) = 3 [1 - (1 - y^{1 / 3})]^{2} \cdot | - \frac{1}{3} y^{- 2 / 3} | = 3 y^{2 / 3} \cdot \frac{1}{3} y^{- 2 / 3}$

And, simplifying we get that the probability density function of Y is:

$f_{Y} (y) = 1$

for $0 < y < 1$ . Again, we shouldn't be surprised by this result, as it is the same result that we obtained using the distribution function technique.

22.3 - Two-to-One Functions

You might have noticed that all of the examples we have looked at so far involved monotonic functions that, because of their one-to-one nature, could therefore be inverted. The question naturally arises then as to how we modify the change-of-variable technique in the situation in which the transformation is not monotonic, and therefore not one-to-one. That's what we'll explore on this page! We'll start with an example in which the transformation is two-to-one. We'll use the distribution function technique to find the p.d.f of the transformed random variable. In so doing, we'll take note of how the change-of-variable technique must be modified to handle the two-to-one portion of the transformation. After summarizing the necessary modification to the change-of-variable technique, we'll take a look at another example using the change-of-variable technique.

Example 22-3

Suppose $X$ is a continuous random variable with probability density function:

$f (x) = \frac{x^{2}}{3}$

for $- 1 < x < 2$ . What is the p.d.f. of $Y = X^{2}$ ?

Solution

First, note that the transformation:

$Y = X^{2}$

is not one-to-one over the interval $- 1 < x < 2$ :

For example, in the interval $- 1 < x < 1$ , if we take the inverse of $Y = X^{2}$ , we get:

$X_{1} = - \sqrt{Y} = v_{1} (Y)$

for $- 1 < x < 0$ , and:

$X_{2} = + \sqrt{Y} = v_{2} (Y)$

for $0 < x < 1$ .

As the graph suggests, the transformation is two-to-one between when $0 < y < 1$ , and one-to-one when $1 < y < 4$ . So, let's use the distribution function technique, separately, over each of these ranges. First, consider when $0 < y < 1$ . In that case:

$F_{Y} (y) = P (Y \leq y) = P (X^{2} \leq y) = P (- \sqrt{y} \leq X \leq \sqrt{y}) = F_{X} (\sqrt{y}) - F_{X} (- \sqrt{y})$

The first equality holds by the definition of the cumulative distribution function. The second equality holds because the transformation of interest is $Y = X^{2}$ . The third equality holds, because when $X^{2} \leq y$ , the random variable $X$ is between the positive and negative square roots of $y$ . And, the last equality holds again by the definition of the cumulative distribution function. Now, taking the derivative of the cumulative distribution function $F (y)$ , we get (from the Fundamental Theorem of Calculus and the Chain Rule) the probability density function $f (y)$ :

$f_{Y} (y) = F_{Y}^{'} (y) = f_{X} (\sqrt{y}) \cdot \frac{1}{2} y^{- 1 / 2} + f_{X} (- \sqrt{y}) \cdot \frac{1}{2} y^{- 1 / 2}$

Using what we know about the probability density function of $X$ :

$f (x) = \frac{x^{2}}{3}$

we get:

$f_{Y} (y) = \frac{(\sqrt{y})^{2}}{3} \cdot \frac{1}{2} y^{- 1 / 2} + \frac{(- \sqrt{y})^{2}}{3} \cdot \frac{1}{2} y^{- 1 / 2}$

And, simplifying, we get:

$f_{Y} (y) = \frac{1}{6} y^{1 / 2} + \frac{1}{6} y^{1 / 2} = \frac{\sqrt{y}}{3}$

for $0 < y < 1$ . Note that it readily becomes apparent that in the case of a two-to-one transformation, we need to sum two terms, each of which arises from a one-to-one transformation.

So, we've found the p.d.f. of $Y$ when $0 < y < 1$ . Now, we have to find the p.d.f. of $Y$ when $1 < y < 4$ . In that case:

$F_{Y} (y) = P (Y \leq y) = P (X^{2} \leq y) = P (X \leq \sqrt{y}) = F_{X} (\sqrt{y})$

The first equality holds by the definition of the cumulative distribution function. The second equality holds because $Y = X^{2}$ . The third equality holds, because when $X^{2} \leq y$ , the random variable $X \leq \sqrt{y}$ . And, the last equality holds again by the definition of the cumulative distribution function. Now, taking the derivative of the cumulative distribution function $F (y)$ , we get (from the Fundamental Theorem of Calculus and the Chain Rule) the probability density function $f (y)$ :

$f_{Y} (y) = F_{Y}^{'} (y) = f_{X} (\sqrt{y}) \cdot \frac{1}{2} y^{- 1 / 2}$

Again, using what we know about the probability density function of $X$ , and simplifying, we get:

$f_{Y} (y) = \frac{(\sqrt{y})^{2}}{3} \cdot \frac{1}{2} y^{- 1 / 2} = \frac{\sqrt{y}}{6}$

for $1 < y < 4$ .

Now that we've seen how the distribution function technique works when we have a two-to-one function, we should now be able to summarize the necessary modifications to the change-of-variable technique.

Generalization

Let $X$ be a continuous random variable with probability density function $f (x)$ for $c_{1} < x < c_{2}$ .

Let $Y = u (X)$ be a continuous two-to-one function of $X$ , which can be “broken up” into two one-to-one invertible functions with:

$X_{1} = v_{1} (Y)$ and $X_{2} = v_{2} (Y)$

Then, the probability density function for the two-to-one portion of $Y$ is:

$f_{Y} (y) = f_{X} (v_{1} (y)) \cdot | v_{1}^{'} (y) | + f_{X} (v_{2} (y)) \cdot | v_{2}^{'} (y) |$

for the “appropriate support” for $y$ . That is, you have to add the one-to-one portions together.
And, the probability density function for the one-to-one portion of $Y$ is, as always:

$f_{Y} (y) = f_{X} (v_{2} (y)) \cdot | v_{2}^{'} (y) |$

for the “appropriate support” for $y$ .

Example 22-4

Suppose $X$ is a continuous random variable with that follows the standard normal distribution with, of course, $- \infty < x < \infty$ . Use the change-of-variable technique to show that the p.d.f. of $Y = X^{2}$ is the chi-square distribution with 1 degree of freedom.

Solution

The transformation $Y = X^{2}$ is two-to-one over the entire support $- \infty < x < \infty$ :

That is, when $- \infty < x < 0$ , we have:

$X_{1} = - \sqrt{Y} = v_{1} (Y)$

and when $0 < x < \infty$ , we have:

$X_{2} = + \sqrt{Y} = v_{2} (Y)$

Then, the change of variable technique tells us that, over the two-to-one portion of the transformation, that is, when $0 < y < \infty$ :

$f_{Y} (y) = f_{X} (\sqrt{y}) \cdot | \frac{1}{2} y^{- 1 / 2} | + f_{X} (- \sqrt{y}) \cdot | - \frac{1}{2} y^{- 1 / 2} |$

Recalling the p.d.f. of the standard normal distribution:

$f_{X} (x) = \frac{1}{\sqrt{2 π}} exp [- \frac{x^{2}}{2}]$

the p.d.f. of $Y$ is then:

$f_{Y} (y) = \frac{1}{\sqrt{2 π}} exp [- \frac{(\sqrt{y})^{2}}{2}] \cdot | \frac{1}{2} y^{- 1 / 2} | + \frac{1}{\sqrt{2 π}} exp [- \frac{(\sqrt{y})^{2}}{2}] \cdot | - \frac{1}{2} y^{- 1 / 2} |$

Adding the terms together, and simplifying a bit, we get:

$f_{Y} (y) = 2 \frac{1}{\sqrt{2 π}} exp [- \frac{y}{2}] \cdot \frac{1}{2} y^{- 1 / 2}$

Crossing out the 2s, recalling that $Γ (1 / 2) = \sqrt{π}$ , and rewriting things just a bit, we should be able to recognize that, with $0 < y < \infty$ , the probability density function of $Y$ :

$f_{Y} (y) = \frac{1}{Γ (1 / 2) 2^{1 / 2}} e^{- y / 2} y^{- 1 / 2}$

is indeed the p.d.f. of a chi-square random variable with 1 degree of freedom!

22.4 - Simulating Observations

Now that we've learned the mechanics of the distribution function and change-of-variable techniques to find the p.d.f. of a transformation of a random variable, we'll now turn our attention for a few minutes to an application of the distribution function technique. In doing so, we'll learn how statistical software, such as Minitab or SAS, generates (or "simulates") 1000 random numbers that follow a particular probability distribution. More specifically, we'll explore how statistical software simulates, say, 1000 random numbers from an exponential distribution with mean $θ = 5$ .

The Idea

If we take a look at the cumulative distribution function of an exponential random variable with a mean of $θ = 5$ :

the idea might just jump out at us. You might notice that the cumulative distribution function $F (x)$ is a number (a cumulative probability, in fact!) between 0 and 1. So, one strategy we might use to generate a 1000 numbers following an exponential distribution with a mean of 5 is:

Generate a $Y \sim U (0, 1)$ random number. That is, generate a number between 0 and 1 such that each number between 0 and 1 is equally likely.
Then, use the inverse of $Y = F (x)$ to get a random number $X = F^{- 1} (y)$ whose distribution function is $F (x)$ . This is, in fact, illustrated on the graph. If $F (x) = 0.8$ , for example, then the inverse $X$ is about 8.
Repeat steps 1 and 2 one thousand times.

By looking at the graph, you should get the idea, by using this strategy, that the shape of the distribution function dictates the probability distribution of the resulting $X$ values. In this case, the steepness of the curve up to about $F (x) = 0.8$ suggests that most of the $X$ values will be less than 8. That's what the probability density function of an exponential random variable with a mean of 5 suggests should happen:

We can even do the calculation, of course, to illustrate this point. If $X$ is an exponential random variable with a mean of 5, then:

$P (X < 8) = 1 - P (X > 8) = 1 - e^{- 8 / 5} = 0.80$

A theorem (naturally!) formalizes our idea of how to simulate random numbers following a particular probability distribution.

Theorem

Let $Y \sim U (0, 1)$ . Let $F (x)$ have the properties of a distribution function of the continuous type with $F (a) = 0$ and $F (b) = 1$ . Suppose that $F (x)$ is strictly increasing on the support $a < x < b$ , where $a$ and $b$ could be $- \infty$ and $\infty$ , respectively. Then, the random variable $X$ defined by:

$X = F^{- 1} (Y)$

is a continuous random variable with cumulative distribution function $F (x)$ .

Proof.

In order to prove the theorem, we need to show that the cumulative distribution function of $X$ is $F (x)$ . That is, we need to show:

$P (X \leq x) = F (x)$

It turns out that the proof is a one-liner! Here it is:

$P (X \leq x) = P (F^{- 1} (Y) \leq x) = P (Y \leq F (x)) = F (x)$

We've set out to prove what we intended, namely that:

$P (X \leq x) = F (x)$

Well, okay, maybe some explanation is needed! The first equality in the one-line proof holds, because:

$X = F^{- 1} (Y)$

Then, the second equality holds because of the red portion of this graph:

That is, when:

$F^{- 1} (Y) \leq x$

is true, so is

$Y \leq F (x)$

Finally, the last equality holds because it is assumed that $Y$ is a uniform(0, 1) random variable, and therefore the probability that $Y$ is less than or equal to some $y$ is, in fact, $y$ itself:

$P (Y \leq y) = F (y) = \int_{0}^{y} d t = y$

That means that the probability that $Y$ is less than or equal to some $F (x)$ is, in fact, $F (x)$ itself:

$P (Y \leq F (x)) = F (x)$

Our one-line proof is complete!

Example 22-5

A student randomly draws the following three uniform(0, 1) numbers:

0.2

0.5

0.9

Use the three uniform(0,1) numbers to generate three random numbers that follow an exponential distribution with mean $θ = 5$ .

Solution

The cumulative distribution function of an exponential random variable with a mean of 5 is:

$y = F (x) = 1 - e^{- x / 5}$

for $0 \leq x < \infty$ . We need to invert the cumulative distribution function, that is, solve for $x$ , in order to be able to determine the exponential(5) random numbers. Manipulating the above equation a bit, we get:

$1 - y = e^{- x / 5}$

Then, taking the natural log of both sides, we get:

$log (1 - y) = - \frac{x}{5}$

And, multiplying both sides by −5, we get:

$x = - 5 log (1 - y)$

for $0 < y < 1$ . Now, it's just a matter of inserting the student's three random U(0,1) numbers into the above equation to get our three exponential(5) random numbers:

If $y = 0.2$ , we get $x = 1.1$
If $y = 0.5$ , we get $x = 3.5$
If $y = 0.9$ , we get $x = 11.5$

We would simply continue the same process — that is, generating $y$ , a random U(0,1) number, inserting y into the above equation, and solving for $x$ — 997 more times if we wanted to generate 1000 exponential(5) random numbers. Of course, we wouldn't really do it by hand, but rather let statistical software do it for us. At least we now understand how random number generation works!

Lesson 23: Transformations of Two Random Variables

Introduction

In this lesson, we consider the situation where we have two random variables and we are interested in the joint distribution of two new random variables which are a transformation of the original one. Such a transformation is called a bivariate transformation. We use a generalization of the change of variables technique which we learned in Lesson 22. We provide examples of random variables whose density functions can be derived through a bivariate transformation.

Objectives

Upon completion of this lesson, you should be able to:

To learn how to use the change-of-variable technique to find the probability distribution of $Y_{1} = u_{1} (X_{1}, X_{2}), Y_{2} = u_{2} (X_{1}, X_{2})$ , a one-to-one transformation of the two random variables $X_{1}$ and $X_{2}$ .

23.1 - Change-of-Variables Technique

Recall, that for the univariate (one random variable) situation: Given $X$ with pdf $f (x)$ and the transformation $Y = u (X)$ with the single-valued inverse $X = v (Y)$ , then the pdf of $Y$ is given by

$\begin{array}{r} g (y) = | v^{'} (y) | f [v (y)] . \end{array}$

Now, suppose $(X_{1}, X_{2})$ has joint density $f (x_{1}, x_{2})$ . and support $S_{X}$ .

Let $(Y_{1}, Y_{2})$ be some function of $(X_{1}, X_{2})$ defined by $Y_{1} = u_{1} (X_{1}, X_{2})$ and $Y_{2} = u_{2} (X_{1}, X_{2})$ with the single-valued inverse given by $X_{1} = v_{1} (Y_{1}, Y_{2})$ and $X_{2} = v_{2} (Y_{1}, Y_{2})$ . Let $S_{Y}$ be the support of $Y_{1}, Y_{2}$ .

Then, we usually find $S_{Y}$ by considering the image of $S_{X}$ under the transformation $(Y_{1}, Y_{2})$ . Say, given $x_{1}, x_{2} \in S_{X}$ , we can find $(y_{1}, y_{2}) \in S_{Y}$ by

$\begin{array}{r} x_{1} = v_{1} (y_{1}, y_{2}), x_{2} = v_{2} (y_{1}, y_{2}) \end{array}$

The joint pdf $Y_{1}$ and $Y_{2}$ is

$\begin{array}{r} g (y_{1}, y_{2}) = | J | f [v_{1} (y_{1}, y_{2}), v_{2} (y_{1}, y_{2})] \end{array}$

In the above expression, $| J |$ refers to the absolute value of the Jacobian, $J$ . The Jacobian, $J$ , is given by

$\begin{array}{r} | \begin{array}{cc} \frac{\partial v_{1} (y_{1}, y_{2})}{\partial y_{1}} & \frac{\partial v_{1} (y_{1}, y_{2})}{\partial y_{2}} \\ \frac{\partial v_{2} (y_{1}, y_{2})}{\partial y_{1}} & \frac{\partial v_{2} (y_{1}, y_{2})}{\partial y_{2}} \end{array} | \end{array}$

i.e. it is the determinant of the matrix

$\begin{array}{r} (\begin{array}{cc} \frac{\partial v_{1} (y_{1}, y_{2})}{\partial y_{1}} & \frac{\partial v_{1} (y_{1}, y_{2})}{\partial y_{2}} \\ \frac{\partial v_{2} (y_{1}, y_{2})}{\partial y_{1}} & \frac{\partial v_{2} (y_{1}, y_{2})}{\partial y_{2}} \end{array}) \end{array}$

Example 23-1

Suppose $X_{1}$ and $X_{2}$ are independent exponential random variables with parameter $λ = 1$ so that

$\begin{aligned} f_{X_{1}} (x_{1}) = e^{- x_{1}} 0 < x_{1} < \infty \\ f_{X_{2}} (x_{2}) = e^{- x_{2}} 0 < x_{2} < \infty \end{aligned}$

The joint pdf is given by

$\begin{array}{r} f (x_{1}, x_{2}) = f_{X_{1}} (x_{1}) f_{X_{2}} (x_{2}) = e^{- x_{1} - x_{2}} 0 < x_{1} < \infty, 0 < x_{2} < \infty \end{array}$

Consider the transformation: $Y_{1} = X_{1} - X_{2}, Y_{2} = X_{1} + X_{2}$ . We wish to find the joint distribution of $Y_{1}$ and $Y_{2}$ .

We have

$\begin{array}{r} x_{1} = \frac{y_{1} + y_{2}}{2}, x_{2} = \frac{y_{2} - y_{1}}{2} \end{array}$

$\begin{array}{r} v_{1} (y_{1}, y_{2}) = \frac{y_{1} + y_{2}}{2}, v_{2} (y_{1}, y_{2}) = \frac{y_{2} - y_{1}}{2} \end{array}$

The Jacobian, $J$ is

$\begin{array}{r} | \begin{array}{cc} \frac{\partial (\frac{y_{1} + y_{2}}{2})}{\partial y_{1}} & \frac{\partial (\frac{y_{1} + y_{2}}{2})}{\partial y_{2}} \\ \frac{\partial (\frac{y_{2} - y_{1}}{2})}{\partial y_{1}} & \frac{\partial (\frac{y_{2} - y_{1}}{2})}{\partial y_{2}} \end{array} | \end{array}$

$\begin{array}{r} = | \begin{array}{cc} \frac{1}{2} & \frac{1}{2} \\ - \frac{1}{2} & \frac{1}{2} \end{array} | = \frac{1}{2} \end{array}$

So,

$\begin{aligned} g (y_{1}, y_{2}) & = e^{- v_{1} (y_{1}, y_{2}) - v_{2} (y_{1}, y_{2})} | \frac{1}{2} | \\ = e^{- [\frac{y_{1} + y_{2}}{2}] - [\frac{y_{2} - y_{1}}{2}]} | \frac{1}{2} | \\ = \frac{e^{- y_{2}}}{2} \end{aligned}$

Now, we determine the support of $(Y_{1}, Y_{2})$ . Since $0 < x_{1} < \infty, 0 < x_{2} < \infty$ , we have $0 < \frac{y_{1} + y_{2}}{2} < \infty, 0 < \frac{y_{2} - y_{1}}{2} < \infty$ or $0 < y_{1} + y_{2} < \infty, 0 < y_{2} - y_{1} < \infty$ . This may be rewritten as $- y_{2} < y_{1} < y_{2}, 0 < y_{2} < \infty$ .

Using the joint pdf, we may find the marginal pdf of $Y_{2}$ as

$\begin{aligned} g (y_{2}) & = \int_{- \infty}^{\infty} g (y_{1}, y_{2}) d y_{1} \\ = \int_{- y_{2}}^{y_{2}} \frac{1}{2} e^{- y_{2}} d y_{1} \\ = \frac{1}{2} {[e^{- y_{2}} y_{1} |}_{y_{1} = - y_{2}}^{y_{1} = y_{2}}] \\ = \frac{1}{2} e^{- y_{2}} (y_{2} + y_{2}) \\ = y_{2} e^{- y_{2}}, 0 < y_{2} < \infty \end{aligned}$

Similarly, we may find the marginal pdf of $Y_{1}$ as

$\begin{array}{r} g (y_{1}) = {\begin{cases} \int_{- y_{1}}^{\infty} \frac{1}{2} e^{- y_{2}} d y_{2} = \frac{1}{2} e^{y_{1}} & - \infty < y_{1} < 0 \\ \int_{y_{1}}^{\infty} \frac{1}{2} e^{- y_{2}} d y_{2} = \frac{1}{2} e^{- y_{1}} & 0 < y_{1} < \infty \end{cases} \end{array}$

Equivalently,

$\begin{aligned} g (y_{1}) = \frac{1}{2} e^{- | y_{1} |} & 0 < y_{1} < \infty \end{aligned}$

This pdf is known as the double exponential or Laplace pdf.

23.2 - Beta Distribution

Let $X_{1}$ and $X_{2}$ have independent gamma distributions with parameters $α, θ$ and $β$ respectively. Therefore, the joint pdf of $X_{1}$ and $X_{2}$ is given by

$\begin{array}{r} f (x_{1}, x_{2}) = \frac{1}{Γ (α) Γ (β) θ^{α + β}} x_{1}^{α - 1} x_{2}^{β - 1} exp (- \frac{x_{1} + x_{2}}{θ}), 0 < x_{1} < \infty, 0 < x_{2} < \infty . \end{array}$

We make the following transformation:

$\begin{array}{r} Y_{1} = \frac{X_{1}}{X_{1} + X_{2}}, Y_{2} = X_{1} + X_{2} \end{array}$

The inverse transformation is given by

$\begin{aligned} X_{1} = Y_{1} Y_{2}, \\ X_{2} = Y_{2} - Y_{1} Y_{2} \end{aligned}$

The Jacobian is

$\begin{array}{r} | \begin{array}{cc} y_{2} & y_{1} \\ - y_{2} & 1 - y_{1} \end{array} | = y_{2} (1 - y_{1}) + y_{1} y_{2} = y_{2} \end{array}$

The joint pdf $g (y_{1}, y_{2})$ is

$\begin{array}{r} g (y_{1}, y_{2}) = | y_{2} | \frac{1}{Γ (α) Γ (β) θ^{α + β}} (y_{1} y_{2})^{α - 1} (y_{2} - y_{1} y_{2})^{β - 1} e^{- y_{2} / θ} \end{array}$

with support is $0 < y_{1} < 1, 0 < y_{2} < \infty$

It may be shown that the marginal pdf of $Y_{1}$ is

$\begin{aligned} g (y_{1}) & = \frac{y_{1}^{α - 1} (1 - y_{1})^{β - 1}}{Γ (α) Γ (β)} \int_{0}^{\infty} \frac{y_{2}^{α + β - 1}}{θ^{α + β}} e^{- y_{2} / θ} d y_{2} g (y_{1}) \\ = \frac{Γ (α + β)}{Γ (α) Γ (β)} y_{1}^{α - 1} (1 - y_{1})^{β - 1}, 0 < y_{1} < 1. \end{aligned}$

$Y_{1}$ is said to have a beta pdf with parameters $α$ and $β$ .

23.3 - F Distribution

We describe a very useful distribution in Statistics known as the F distribution.

Let $U$ and $V$ be independent chi-square variables with $r_{1}$ and $r_{2}$ degrees of freedom, respectively. The joint pdf is

$\begin{array}{r} g (u, v) = \frac{u^{r_{1} / 2 - 1} e^{- u / 2} v^{r_{2} / 2 - 1} e^{- v / 2}}{Γ (r_{1} / 2) 2^{r_{1} / 2} Γ (r_{2} / 2) 2^{r_{2} / 2}}, 0 < u < \infty, 0 < v < \infty \end{array}$

Define the random variable $W = \frac{U / r_{1}}{V / r_{2}}$

This time we use the distribution function technique described in lesson 22,

$\begin{array}{r} F (w) = P (W \leq w) = P (\frac{U / r_{1}}{V / r_{2}} \leq w) = P (U \leq \frac{r_{1}}{r_{2}} w V) = \int_{0}^{\infty} \int_{0}^{(r_{1} / r_{2}) w v} g (u, v) d u d v \end{array}$

$\begin{array}{r} F (w) = \frac{1}{Γ (r_{1} / 2) Γ (r_{2} / 2)} \int_{0}^{\infty} [\int_{0}^{(r_{1} / r_{2}) w v} \frac{u^{r_{1} / 2 - 1} e^{- u / 2}}{2^{(r_{1} + r_{2}) / 2}} d u] v^{r_{1} / 2 - 1} e^{- v / 2} d v \end{array}$

By differentiating the cdf , it can be shown that $f (w) = F^{'} (w)$ is given by

$\begin{array}{r} f (w) = \frac{{(r_{1} / r_{2})}^{r_{1} / 2} Γ [(r_{1} + r_{2}) / 2] w^{r_{1} / 2 - 1}}{Γ (r_{1} / 2) Γ (r_{2} / 2) {[1 + (r_{1} w / r_{2})]}^{(r_{1} + r_{2}) / 2}}, w > 0 \end{array}$

A random variable with the pdf $f (w)$ is said to have an F distribution with $r_{1}$ and $r_{2}$ degrees of freedom. We write this as $F (r_{1}, r_{2})$ . Table VII in Appendix B of the textbook can be used to find probabilities for a random variable with the $F (r_{1}, r_{2})$ distribution.

It contains the F-values for various cumulative probabilities $(0.95, 0.975, 0.99)$ (or the equivalent upper − $α$ th probabilities $(0.05, 0.025, 0.01)$ ) of various $F (r 1, r 2)$ distributions.

When using this table, it is helpful to note that if a random variable (say, $W$ ) has the $F (r_{1}, r_{2})$ distribution, then its inverse $\frac{1}{W}$ has the $F (r_{2}, r_{1})$ distribution.

Illustration

The shape of the F distribution is determined by the degrees of freedom $r_{1}$ and $r_{2}$ . The histogram below shows how an F random variable is generated using 1000 observations each from two chi-square random variables ( $U$ and $V$ ) with degrees of freedom 4 and 8 respectively and forming the ratio $\frac{U / 4}{V / 8}$ .

The lower plot (below histogram) illustrates how the shape of an F distribution changes with the degrees of freedom $r_{1}$ and $r_{2}$ .

Lesson 24: Several Independent Random Variables

Introduction

In the previous lessons, we explored functions of random variables. We'll do the same in this lesson, too, except here we'll add the requirement that the random variables be independent, and in some cases, identically distributed. Suppose, for example, that we were interested in determining the average weight of the thousands of pumpkins grown on a pumpkin farm. Since we couldn't possibly weigh all of the pumpkins on the farm, we'd want to weigh just a small random sample of pumpkins. If we let:

$X_{1}$ denote the weight of the first pumpkin sampled
$X_{2}$ denote the weight of the second pumpkin sampled
...
$X_{n}$ denote the weight of the $n^{t h}$ pumpkin sampled

then we could imagine calculating the average weight of the sampled pumpkins as:

$\bar{X} = \frac{X_{1} + X_{2} + \dots + X_{n}}{n}$

Now, because the pumpkins were randomly sampled, we wouldn't expect the weight of one pumpkin, say $X_{1}$ , to affect the weight of another pumpkin, say $X_{2}$ . Therefore, $X_{1}, X_{2}, \dots, X_{n}$ can be assumed to be independent random variables. And, since $\bar{X}$ , as defined above, is a function of those independent random variables, it too must be a random variable with a certain probability distribution, a certain mean and a certain variance. Our work in this lesson will all be directed towards the end goal of being able to calculate the mean and variance of the random variable $\bar{X}$ . We'll learn a number things along the way, of course, including a formal definition of a random sample, the expectation of a product of independent variables, and the mean and variance of a linear combination of independent random variables.

Objectives

Upon completion of this lesson, you should be able to:

To get the big picture for the remainder of the course.
To learn a formal definition of a random sample.
To learn what i.i.d. means.
To learn how to find the expectation of a function of $n$ independent random variables.
To learn how to find the expectation of a product of functions of $n$ independent random variables.
To learn how to find the mean and variance of a linear combination of random variables.
To learn that the expected value of the sample mean is $μ$ .
To learn that the variance of the sample mean is $\frac{σ^{2}}{n}$ .
To understand all of the proofs presented in the lesson.
To be able to apply the methods learned in this lesson to new problems.

24.1 - Some Motivation

Consider the population of 8 million college students. Suppose we are interested in determining $μ$ , the unknown mean distance (in miles) from the students' schools to their hometowns. We can't possibly determine the distance for each of the 8 million students in order to calculate the population mean $μ$ and the population variance $σ^{2}$ . We could, however, take a random sample of, say, 100 college students, determine:

$X_{i}$ = the distance (in miles) from the home of student $i$ for $i = 1, 2, \dots, 100$

and use the resulting data to learn about the population of college students. How could we obtain that random sample though? Would it be okay to stand outside a major classroom building on the Penn State campus, such as the Willard Building, and ask random students how far they are from their hometown? Probably not! The average distance for Penn State students probably differs greatly from that of college students attending a school in a major city, such as, say The University of California in Los Angeles (UCLA). We need to use a method that ensures that the sample is representative of all college students in the population, not just a subset of the students. Any method that ensures that our sample is truly random will suffice. The following definition formalizes what makes a sample truly random.

Definition. The random variables $X_{i}$ constitute a random sample of size $n$ if and only if:

the $X_{i}$ are independent, and
the $X_{i}$ are identically distributed, that is, each $X_{i}$ comes from the same distribution $f (x)$ with mean $μ$ and variance $σ^{2}$ .

We say that the $X_{i}$ are "i.i.d." (The first i. stands for independent, and the i.d. stands for identically distributed.)

Now, once we've obtained our (truly) random sample, we'll probably want to use the resulting data to calculate the sample mean:

$\bar{X} = \frac{\sum_{i = 1}^{n} X_{i}}{n} = \frac{X_{1} + X_{2} + \dots + X_{100}}{100}$

and sample variance:

$S^{2} = \frac{\sum_{i = 1}^{n} (X_{i} - \bar{X})^{2}}{n - 1} = \frac{(X_{1} - \bar{X})^{2} + \dots + (X_{100} - \bar{X})^{2}}{99}$

In Stat 415, we'll learn that the sample mean $\bar{X}$ is the "best" estimate of the population mean $μ$ and the sample variance $S^{2}$ is the "best" estimate of the population variance $σ^{2}$ . (We'll also learn in what sense the estimates are "best.") Now, before we can use the sample mean and sample variance to draw conclusions about the possible values of the unknown population mean $μ$ and unknown population variance $σ^{2}$ , we need to know how $\bar{X}$ and $S^{2}$ behave. That is, we need to know: ^[3]

the probability distribution of $\bar{X}$ and $S^{2}$
the theoretical mean of of $\bar{X}$ and $S^{2}$
the theoretical variance of $\bar{X}$ and $S^{2}$

Now, note that $\bar{X}$ and $S^{2}$ are sums of independent random variables. That's why we are working in a lesson right now called Several Independent Random Variables. In this lesson, we'll learn about the mean and variance of the random variable $\bar{X}$ . Then, in the lesson called Random Functions Associated with Normal Distributions, we'll add the assumption that the $X_{i}$ are measurements from a normal distribution with mean $μ$ and variance $σ^{2}$ to see what we can learn about the probability distribution of $\bar{X}$ and $S^{2}$ . In the lesson called The Central Limit Theorem, we'll learn that those results still hold even if our measurements aren't from a normal distribution, providing we have a large enough sample. Along the way, we'll pick up a new tool for our toolbox, namely The Moment-Generating Function Technique. And in the final lesson for the Section (and Course!), we'll see another application of the Central Limit Theorem, namely using the normal distribution to approximate discrete distributions, such as the binomial and Poisson distributions. With our motivation presented, and our curiosity now piqued, let's jump right in and get going!

24.2 - Expectations of Functions of Independent Random Variables

One of our primary goals of this lesson is to determine the theoretical mean and variance of the sample mean:

$\bar{X} = \frac{X_{1} + X_{2} + \dots + X_{n}}{n}$

Now, assume the $X_{i}$ are independent, as they should be if they come from a random sample. Then, finding the theoretical mean of the sample mean involves taking the expectation of a sum of independent random variables:

$E (\bar{X}) = \frac{1}{n} E (X_{1} + X_{2} + \dots + X_{n})$

That's why we'll spend some time on this page learning how to take expectations of functions of independent random variables! A simple example illustrates that we already have a number of techniques sitting in our toolbox ready to help us find the expectation of a sum of independent random variables.

Example 24-1

Suppose we toss a penny three times. Let $X_{1}$ denote the number of heads that we get in the three tosses. And, suppose we toss a second penny two times. Let $X_{2}$ denote the number of heads we get in those two tosses. If we let:

$Y = X_{1} + X_{2}$

then $Y$ denotes the number of heads in five tosses. Note that the random variables $X_{1}$ and $X_{2}$ are independent and therefore $Y$ is the sum of independent random variables. Furthermore, we know that:

$X_{1}$ is a binomial random variable with $n = 3$ and $p = \frac{1}{2}$
$X_{2}$ is a binomial random variable with $n = 2$ and $p = \frac{1}{2}$
$Y$ is a binomial random variable with $n = 5$ and $p = \frac{1}{2}$

What is the mean of $Y$ , the sum of two independent random variables? And, what is the variance of $Y$ ?

Solution

We can calculate the mean and variance of $Y$ in three different ways.

By recognizing that $Y$ is a binomial random variable with $n = 5$ and $p = \frac{1}{2}$ , we can use what know about the mean and variance of a binomial random variable, namely that the mean of $Y$ is:

$E (Y) = n p = 5 (\frac{1}{2}) = \frac{5}{2}$

and the variance of $Y$ is:

$V a r (Y) = n p (1 - p) = 5 (\frac{1}{2}) (\frac{1}{2}) = \frac{5}{4}$

Since sums of independent random variables are not always going to be binomial, this approach won't always work, of course. It would be good to have alternative methods in hand!
We could use the linear operator property of expectation. Before doing so, it would be helpful to note that the mean of $X_{1}$ is:

$E (X_{1}) = n p = 3 (\frac{1}{2}) = \frac{3}{2}$

and the mean of $X_{2}$ is:

$E (X_{2}) = n p = 2 (\frac{1}{2}) = 1$

Now, using the property, we get that the mean of $Y$ is (thankfully) again $\frac{5}{2}$ :

$E (Y) = E (X_{1} + X_{2}) = E (X_{1}) + E (X_{2}) = \frac{3}{2} + 1 = \frac{5}{2}$

Recall that the second equality comes from the linear operator property of expectation. Now, using the linear operator property of expectation to find the variance of $Y$ takes a bit more work. First, we should note that the variance of $X_{1}$ is:

$V a r (X_{1}) = n p (1 - p) = 3 (\frac{1}{2}) (\frac{1}{2}) = \frac{3}{4}$

and the variance of $X_{2}$ is:

$V a r (X_{2}) = n p (1 - p) = 2 (\frac{1}{2}) (\frac{1}{2}) = \frac{1}{2}$

Now, we can (thankfully) show again that the variance of $Y$ is $\frac{5}{4}$ :

https://www.youtube.com/watch/U0Wcjddx5qE ^[4]

Okay, as if two methods aren't enough, we still have one more method we could use.
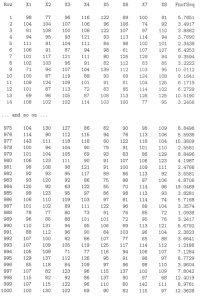
We could use the independence of the two random variables $X_{1}$ and $X_{2}$ , in conjunction with the definition of expected value of $Y$ as we know it. First, using the binomial formula, note that we can present the probability mass function of $X_{1}$ in tabular form as:

$x_{1}$ 0 1 2 3

$f (x_{1})$ $\frac{1}{8}$ $\frac{3}{8}$ $\frac{3}{8}$ $\frac{1}{8}$

And, we can present the probability mass function of $X_{2}$ in tabular form as well:

$x_{2}$ 0 1 2

$f (x_{2})$ $\frac{1}{4}$ $\frac{2}{4}$ $\frac{1}{4}$

Now, recall that if $X_{1}$ and $X_{2}$ are independent random variables, then:

$f (x_{1}, x_{2}) = f (x_{1}) \cdot f (x_{2})$

We can use this result to help determine $g (y)$ , the probability mass function of $Y$ . First note that, since $Y$ is the sum of $X_{1}$ and $X_{2}$ , the support of $Y$ is {0, 1, 2, 3, 4 and 5}. Now, by brute force, we get:

$g (0) = P (Y = 0) = P (X_{1} = 0, X_{2} = 0) = f (0, 0) = f_{X_{1}} (0) \cdot f_{X_{2}} (0) = \frac{1}{8} \cdot \frac{1}{4} = \frac{1}{32}$

The second equality comes from the fact that the only way that $Y$ can equal 0 is if $X_{1} = 0$ and $X_{2} = 0$ , and the fourth equality comes from the independence of $X_{1}$ and $X_{2}$ . We can make a similar calculation to find the probability that $Y = 1$ :

$g (1) = P (X_{1} = 0, X_{2} = 1) + P (X_{1} = 1, X_{2} = 0) = f_{X_{1}} (0) \cdot f_{X_{2}} (1) + f_{X_{1}} (1) \cdot f_{X_{2}} (0) = \frac{1}{8} \cdot \frac{2}{4} + \frac{3}{8} \cdot \frac{1}{4} = \frac{5}{32}$

The first equality comes from the fact that there are two (mutually exclusive) ways that $Y$ can equal 1, namely if $X_{1} = 0$ and $X_{2} = 1$ or if $X_{1} = 1$ and $X_{2} = 0$ . The second equality comes from the independence of $X_{1}$ and $X_{2}$ . We can make similar calculations to find $g (2), g (3), g (4)$ , and $g (5)$ . Once we've done that, we can present the p.m.f. of $Y$ in tabular form as:

$y = x_{1} + x_{2}$ 0 1 2 3 4 5

$g (y)$ $\frac{1}{32}$ $\frac{5}{32}$ $\frac{10}{32}$ $\frac{10}{32}$ $\frac{5}{32}$ $\frac{1}{32}$

Then, it is a straightforward calculation to use the definition of the expected value of a discrete random variable to determine that (again!) the expected value of $Y$ is $\frac{5}{2}$ :

$E (Y) = 0 (\frac{1}{32}) + 1 (\frac{5}{32}) + 2 (\frac{10}{32}) + \dots + 5 (\frac{1}{32}) = \frac{80}{32} = \frac{5}{2}$

The variance of $Y$ can be calculated similarly. (Do you want to calculate it one more time?!)

The following summarizes the method we've used here in calculating the expected value of $Y$ :

$\begin{aligned} E (Y) = E (X_{1} + X_{2}) & = \sum_{x_{1} \in S_{1}} \sum_{x_{2} \in S_{2}} (x_{1} + x_{2}) f (x_{1}, x_{2}) \\ = \sum_{x_{1} \in S_{1}} \sum_{x_{2} \in S_{2}} (x_{1} + x_{2}) f (x_{1}) f (x_{2}) \\ = \sum_{y \in S} y g (y) \end{aligned}$

The first equality comes, of course, from the definition of $Y$ . The second equality comes from the definition of the expectation of a function of discrete random variables. The third equality comes from the independence of the random variables $X_{1}$ and $X_{2}$ . And, the fourth equality comes from the definition of the expected value of $Y$ , as well as the fact that $g (y)$ can be determined by summing the appropriate joint probabilities of $X_{1}$ and $X_{2}$ .

$x_{1}$	0	1	2	3
$f (x_{1})$	$\frac{1}{8}$	$\frac{3}{8}$	$\frac{3}{8}$	$\frac{1}{8}$

$x_{2}$	0	1	2
$f (x_{2})$	$\frac{1}{4}$	$\frac{2}{4}$	$\frac{1}{4}$

$y = x_{1} + x_{2}$	0	1	2	3	4	5
$g (y)$	$\frac{1}{32}$	$\frac{5}{32}$	$\frac{10}{32}$	$\frac{10}{32}$	$\frac{5}{32}$	$\frac{1}{32}$

The following theorem formally states the third method we used in determining the expected value of $Y$ , the function of two independent random variables. We state the theorem without proof. (If you're interested, you can find a proof of it in Hogg, McKean and Craig, 2005.)

Theorem

Let $X_{1}, X_{2}, \dots, X_{n}$ be $n$ independent random variables that, by their independence, have the joint probability mass function:

$f_{1} (x_{1}) f_{2} (x_{2}) \dots f_{n} (x_{n})$

Let the random variable $Y = u (X_{1}, X_{2}, \dots, X_{n})$ have the probability mass function $g (y)$ . Then, in the discrete case:

$E (Y) = \sum_{y} y g (y) = \sum_{x_{1}} \sum_{x_{2}} \dots \sum_{x_{n}} u (x_{1}, x_{2}, \dots, x_{n}) f_{1} (x_{1}) f_{2} (x_{2}) \dots f_{n} (x_{n})$

provided that these summations exist. For continuous random variables, integrals replace the summations.

In the special case that we are looking for the expectation of the product of functions of $n$ independent random variables, the following theorem will help us out.

Theorem

X_{1}, X_{2}, \dots, X_{n}

are independent random variables and, for

i = 1, 2, \dots, n

, the expectation

E [u_{i} (X_{i})]

exists, then:

$E [u_{1} (x_{1}) u_{2} (x_{2}) \dots u_{n} (x_{n})] = E [u_{1} (x_{1})] E [u_{2} (x_{2})] \dots E [u_{n} (x_{n})]$

That is, the expectation of the product is the product of the expectations.

Proof

For the sake of concreteness, let's assume that the random variables are discrete. Then, the definition of expectation gives us:

$E [u_{1} (x_{1}) u_{2} (x_{2}) \dots u_{n} (x_{n})] = \sum_{x_{1}} \sum_{x_{2}} \dots \sum_{x_{n}} u_{1} (x_{1}) u_{2} (x_{2}) \dots u_{n} (x_{n}) f_{1} (x_{1}) f_{2} (x_{2}) \dots f_{n} (x_{n})$

Then, since functions that don't depend on the index of the summation signs can get pulled through the summation signs, we have:

$E [u_{1} (x_{1}) u_{2} (x_{2}) \dots u_{n} (x_{n})] = \sum_{x_{1}} u_{1} (x_{1}) f_{1} (x_{1}) \sum_{x_{2}} u_{2} (x_{2}) f_{2} (x_{2}) \dots \sum_{x_{n}} u_{n} (x_{n}) f_{n} (x_{n})$

Then, by the definition, in the discrete case, of the expected value of $u_{i} (X_{i})$ , our expectation reduces to:

$E [u_{1} (x_{1}) u_{2} (x_{2}) \dots u_{n} (x_{n})] = E [u_{1} (x_{1})] E [u_{2} (x_{2})] \dots E [u_{n} (x_{n})]$

Our proof is complete. If our random variables are instead continuous, the proof would be similar. We would just need to make the obvious change of replacing the summation signs with integrals.

Let's return to our example in which we toss a penny three times, and let $X_{1}$ denote the number of heads that we get in the three tosses. And, again toss a second penny two times, and let $X_{2}$ denote the number of heads we get in those two tosses. In our previous work, we learned that:

$E (X_{1}) = \frac{3}{2}$ and $Var (X_{1}) = \frac{3}{4}$
$E (X_{2}) = 1$ and $Var (X_{2}) = \frac{1}{2}$

What is the expected value of $X_{1}^{2} X_{2}$ ?

Solution

We'll use the fact that the expectation of the product is the product of the expectations:

https://www.youtube.com/watch/hWng9Q0iZSM ^[5]

24.3 - Mean and Variance of Linear Combinations

We are still working towards finding the theoretical mean and variance of the sample mean:

$\bar{X} = \frac{X_{1} + X_{2} + \dots + X_{n}}{n}$

If we re-write the formula for the sample mean just a bit:

$\bar{X} = \frac{1}{n} X_{1} + \frac{1}{n} X_{2} + \dots + \frac{1}{n} X_{n}$

we can see more clearly that the sample mean is a linear combination of the random variables $X_{1}, X_{2}, \dots, X_{n}$ . That's why the title and subject of this page! That is, here on this page, we'll add a few a more tools to our toolbox, namely determining the mean and variance of a linear combination of random variables $X_{1}, X_{2}, \dots, X_{n}$ . Before presenting and proving the major theorem on this page, let's revisit again, by way of example, why we would expect the sample mean and sample variance to have a theoretical mean and variance.

Example 24-2

A statistics instructor conducted a survey in her class. The instructor was interested in learning how many siblings, on average, the students at Penn State University have? She took a random sample of $n = 4$ students, and asked each student how many siblings he/she has. The resulting data were: 0, 2, 1, 1. In an attempt to summarize the data she collected, the instructor calculated the sample mean and sample variance, getting:

$\bar{X} = \frac{4}{4} = 1$ and $S^{2} = \frac{(0 - 1)^{2} + (2 - 1)^{2} + (1 - 1)^{2} + (1 - 1)^{2}}{3} = \frac{2}{3}$

The instructor realized though, that if she had asked a different sample of $n = 4$ students how many siblings they have, she'd probably get different results. So, she took a different random sample of $n = 4$ students. The resulting data were: 4, 1, 2, 1. Calculating the sample mean and variance once again, she determined:

$\bar{X} = \frac{8}{4} = 2$ and $S^{2} = \frac{(4 - 2)^{2} + (1 - 2)^{2} + (2 - 2)^{2} + (1 - 2)^{2}}{3} = \frac{6}{3} = 2$

Hmmm, the instructor thought that was quite a different result from the first sample, so she decided to take yet another sample of $n = 4$ students. Doing so, the resulting data were: 5, 3, 2, 2. Calculating the sample mean and variance yet again, she determined:

$\bar{X} = \frac{12}{4} = 3$ and $S^{2} = \frac{(5 - 3)^{2} + (3 - 3)^{2} + (2 - 3)^{2} + (2 - 3)^{2}}{3} = \frac{6}{3} = 2$

That's enough of this! I think you can probably see where we are going with this example. It is very clear that the values of the sample mean $\bar{X}$ and the sample variance $S^{2}$ depend on the selected random sample. That is, $\bar{X}$ and $S^{2}$ are continuous random variables in their own right. Therefore, they themselves should each have a particular:

probability distribution (called a "sampling distribution"),
mean, and
variance.

We are still in the hunt for all three of these items. The next theorem will help move us closer towards finding the mean and variance of the sample mean $\bar{X}$ .

Theorem

Suppose $X_{1}, X_{2}, \dots, X_{n}$ are $n$ independent random variables with means $μ_{1}, μ_{2}, \dots, μ_{n}$ and variances $σ_{1}^{2}, σ_{2}^{2}, \dots, σ_{n}^{2}$ .

Then, the mean and variance of the linear combination $Y = \sum_{i = 1}^{n} a_{i} X_{i}$ , where $a_{1}, a_{2}, \dots, a_{n}$ are real constants are:

$μ_{Y} = \sum_{i = 1}^{n} a_{i} μ_{i}$

and:

$σ_{Y}^{2} = \sum_{i = 1}^{n} a_{i}^{2} σ_{i}^{2}$

respectively.

Proof

Let's start with the proof for the mean first:

https://www.youtube.com/watch/qUCY5u2vpEo ^[6]

Now for the proof for the variance. Starting with the definition of the variance of $Y$ , we have:

$σ_{Y}^{2} = V a r (Y) = E [(Y - μ_{Y})^{2}]$

Now, substituting what we know about $Y$ and the mean of $Y$ Y, we have:

$σ_{Y}^{2} = E [{(\sum_{i = 1}^{n} a_{i} X_{i} - \sum_{i = 1}^{n} a_{i} μ_{i})}^{2}]$

Because the summation signs have the same index ( $i = 1$ to $n$ ), we can replace the two summation signs with one summation sign:

$σ_{Y}^{2} = E [{(\sum_{i = 1}^{n} (a_{i} X_{i} - a_{i} μ_{i}))}^{2}]$

And, we can factor out the constants $a_{i}$ :

$σ_{Y}^{2} = E [{(\sum_{i = 1}^{n} a_{i} (X_{i} - μ_{i}))}^{2}]$

Now, let's rewrite the squared term as the product of two terms. In doing so, use an index of $i$ on the first summation sign, and an index of $j$ on the second summation sign:

$σ_{Y}^{2} = E [(\sum_{i = 1}^{n} a_{i} (X_{i} - μ_{i})) (\sum_{j = 1}^{n} a_{j} (X_{j} - μ_{j}))]$

Now, let's pull the summation signs together:

$σ_{Y}^{2} = E [\sum_{i = 1}^{n} \sum_{j = 1}^{n} a_{i} a_{j} (X_{i} - μ_{i}) (X_{j} - μ_{j})]$

Then, by the linear operator property of expectation, we can distribute the expectation:

$σ_{Y}^{2} = \sum_{i = 1}^{n} \sum_{j = 1}^{n} a_{i} a_{j} E [(X_{i} - μ_{i}) (X_{j} - μ_{j})]$

Now, let's rewrite the variance of $Y$ by evaluating each of the terms from $i = 1$ to $n$ and $j = 1$ to $n$ . In doing so, recognize that when $i = j$ , the expectation term is the variance of $X_{i}$ , and when $i \neq j$ , the expectation term is the covariance between $X_{i}$ and $X_{j}$ , which by the assumed independence, is 0:

var Y

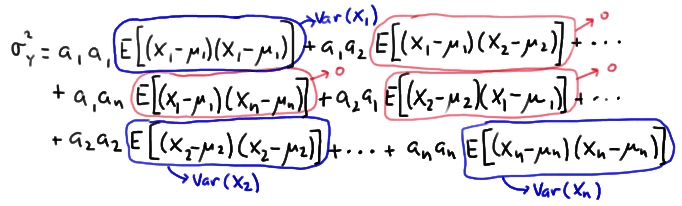
Simplifying then, we get:

$σ_{Y}^{2} = a_{1}^{2} E [(X_{1} - μ_{1})^{2}] + a_{2}^{2} E [(X_{2} - μ_{2})^{2}] + \dots + a_{n}^{2} E [(X_{n} - μ_{n})^{2}]$

And, simplifying yet more using variance notation:

$σ_{Y}^{2} = a_{1}^{2} σ_{1}^{2} + a_{2}^{2} σ_{2}^{2} + \dots + a_{n}^{2} σ_{n}^{2}$

Finally, we have:

$σ_{Y}^{2} = \sum_{i = 1}^{n} a_{i}^{2} σ_{i}^{2}$

as was to be proved.

Example 24-3

Let $X_{1}$ and $X_{2}$ be independent random variables. Suppose the mean and variance of $X_{1}$ are 2 and 4, respectively. Suppose, the mean and variance of $X_{2}$ are 3 and 5 respectively. What is the mean and variance of $X_{1} + X_{2}$ ?

Solution

The mean of the sum is:

$E (X_{1} + X_{2}) = E (X_{1}) + E (X_{2}) = 2 + 3 = 5$

and the variance of the sum is:

$V a r (X_{1} + X_{2}) = (1)^{2} V a r (X_{1}) + (1)^{2} V a r (X_{2}) = 4 + 5 = 9$

What is the mean and variance of $X_{1} - X_{2}$ ?

Solution

The mean of the difference is:

$E (X_{1} - X_{2}) = E (X_{1}) - E (X_{2}) = 2 - 3 = - 1$

and the variance of the difference is:

$V a r (X_{1} - X_{2}) = V a r (X_{1} + (- 1) X_{2}) = (1)^{2} V a r (X_{1}) + (- 1)^{2} V a r (X_{2}) = 4 + 5 = 9$

That is, the variance of the difference in the two random variables is the same as the variance of the sum of the two random variables.

What is the mean and variance of $3 X_{1} + 4 X_{2}$ ?

Solution

The mean of the linear combination is:

$E (3 X_{1} + 4 X_{2}) = 3 E (X_{1}) + 4 E (X_{2}) = 3 (2) + 4 (3) = 18$

and the variance of the linear combination is:

$V a r (3 X_{1} + 4 X_{2}) = (3)^{2} V a r (X_{1}) + (4)^{2} V a r (X_{2}) = 9 (4) + 16 (5) = 116$

24.4 - Mean and Variance of Sample Mean

We'll finally accomplish what we set out to do in this lesson, namely to determine the theoretical mean and variance of the continuous random variable $\bar{X}$ . In doing so, we'll discover the major implications of the theorem that we learned on the previous page.

Let $X_{1}, X_{2}, \dots, X_{n}$ be a random sample of size $n$ from a distribution (population) with mean $μ$ and variance $σ^{2}$ . What is the mean, that is, the expected value, of the sample mean $\bar{X}$ ?

Solution

Starting with the definition of the sample mean, we have:

$E (\bar{X}) = E (\frac{X_{1} + X_{2} + \dots + X_{n}}{n})$

Then, using the linear operator property of expectation, we get:

$E (\bar{X}) = \frac{1}{n} [E (X_{1}) + E (X_{2}) + \dots + E (X_{n})]$

Now, the $X_{i}$ are identically distributed, which means they have the same mean $μ$ . Therefore, replacing $E (X_{i})$ with the alternative notation $μ$ , we get:

$E (\bar{X}) = \frac{1}{n} [μ + μ + \dots + μ]$

Now, because there are $n$ $μ$ 's in the above formula, we can rewrite the expected value as:

$E (\bar{X}) = \frac{1}{n} [n μ] = μ$

We have shown that the mean (or expected value, if you prefer) of the sample mean $\bar{X}$ is $μ$ . That is, we have shown that the mean of $\bar{X}$ is the same as the mean of the individual $X_{i}$ .

Let $X_{1}, X_{2}, \dots, X_{n}$ be a random sample of size $n$ from a distribution (population) with mean $μ$ and variance $σ^{2}$ . What is the variance of $\bar{X}$ ?

Solution

Starting with the definition of the sample mean, we have:

$V a r (\bar{X}) = V a r (\frac{X_{1} + X_{2} + \dots + X_{n}}{n})$

Rewriting the term on the right so that it is clear that we have a linear combination of $X_{i}$ 's, we get:

$V a r (\bar{X}) = V a r (\frac{1}{n} X_{1} + \frac{1}{n} X_{2} + \dots + \frac{1}{n} X_{n})$

Then, applying the theorem on the last page, we get:

$V a r (\bar{X}) = \frac{1}{n^{2}} V a r (X_{1}) + \frac{1}{n^{2}} V a r (X_{2}) + \dots + \frac{1}{n^{2}} V a r (X_{n})$

Now, the $X_{i}$ are identically distributed, which means they have the same variance $σ^{2}$ . Therefore, replacing $Var (X_{i})$ with the alternative notation $σ^{2}$ , we get:

$V a r (\bar{X}) = \frac{1}{n^{2}} [σ^{2} + σ^{2} + \dots + σ^{2}]$

Now, because there are $n$ $σ^{2}$ 's in the above formula, we can rewrite the expected value as:

$V a r (\bar{X}) = \frac{1}{n^{2}} [n σ^{2}] = \frac{σ^{2}}{n}$

Our result indicates that as the sample size $n$ increases, the variance of the sample mean decreases. That suggests that on the previous page, if the instructor had taken larger samples of students, she would have seen less variability in the sample means that she was obtaining. This is a good thing, but of course, in general, the costs of research studies no doubt increase as the sample size $n$ increases. There is always a trade-off!

24.5 - More Examples

On this page, we'll just take a look at a few examples that use the material and methods we learned about in this lesson.

Example 24-4

If $X_{1}, X_{2}, \dots, X_{n}$ are a random sample from a population with mean $μ$ and variance $σ^{2}$ , then what is:

$E [(X_{i} - μ) (X_{j} - μ)]$

for $i \neq j$ , $i = 1, 2, \dots, n$ ?

Solution

The fact that $X_{1}, X_{2}, \dots, X_{n}$ constitute a random sample tells us that (1) $X_{i}$ is independent of $X_{j}$ , for all $i \neq j$ , and (2) the $X_{i}$ are identically distributed. Now, we know from our previous work that if $X_{i}$ is independent of $X_{j}$ , for $i \neq j$ , then the covariance between $X_{i}$ is independent of $X_{j}$ is 0. That is:

$E [(X_{i} - μ) (X_{j} - μ)] = C o v (X_{i}, X_{j}) = 0$

Example 24-5

Let $X_{1}, X_{2}, X_{3}$ be a random sample of size $n = 3$ from a distribution with the geometric probability mass function:

$f (x) = (\frac{3}{4}) {(\frac{1}{4})}^{x - 1}$

for $x = 1, 2, 3, \dots$ . What is $P (max X_{i} \leq 2)$ ?

Solution

The only way that the maximum of the $X_{i}$ will be less than or equal to 2 is if all of the $X_{i}$ are less than or equal to 2. That is:

$P (max X_{i} \leq 2) = P (X_{1} \leq 2, X_{2} \leq 2, X_{3} \leq 2)$

Now, because $X_{1}, X_{2}, X_{3}$ are a random sample, we know that (1) $X_{i}$ is independent of $X_{j}$ , for all $i \neq j$ , and (2) the $X_{i}$ are identically distributed. Therefore:

$P (max X_{i} \leq 2) = P (X_{1} \leq 2) P (X_{2} \leq 2) P (X_{3} \leq 2) = [P (X_{1} \leq 2)]^{3}$

The first equality comes from the independence of the $X_{i}$ , and the second equality comes from the fact that the $X_{i}$ are identically distributed. Now, the probability that $X_{1}$ is less than or equal to 2 is:

$P (X \leq 2) = P (X = 1) + P (X = 2) = (\frac{3}{4}) {(\frac{1}{4})}^{1 - 1} + (\frac{3}{4}) {(\frac{1}{4})}^{2 - 1} = \frac{3}{4} + \frac{3}{16} = \frac{15}{16}$

Therefore, the probability that the maximum of the $X_{i}$ is less than or equal to 2 is:

$P (max X_{i} \leq 2) = [P (X_{1} \leq 2)]^{3} = {(\frac{15}{16})}^{3} = 0.824$

Lesson 25: The Moment-Generating Function Technique

Overview

In the previous lesson, we learned that the expected value of the sample mean $\bar{X}$ is the population mean $μ$ . We also learned that the variance of the sample mean $\bar{X}$ is $\frac{σ^{2}}{n}$ , that is, the population variance divided by the sample size $n$ . We have not yet determined the probability distribution of the sample mean when, say, the random sample comes from a normal distribution with mean $μ$ and variance $σ^{2}$ . We are going to tackle that in the next lesson! Before we do that, though, we are going to want to put a few more tools into our toolbox. We already have learned a few techniques for finding the probability distribution of a function of random variables, namely the distribution function technique and the change-of-variable technique. In this lesson, we'll learn yet another technique called the moment-generating function technique. We'll use the technique in this lesson to learn, among other things, the distribution of sums of chi-square random variables, Then, in the next lesson, we'll use the technique to find (finally) the probability distribution of the sample mean when the random sample comes from a normal distribution with mean $μ$ and variance $σ^{2}$ .

Objectives

Upon completion of this lesson, you should be able to:

To refresh our memory of the uniqueness property of moment-generating functions.
To learn how to calculate the moment-generating function of a linear combination of $n$ independent random variables.
To learn how to calculate the moment-generating function of a linear combination of $n$ independent and identically distributed random variables.
To learn the additive property of independent chi-square random variables.
To use the moment-generating function technique to prove the additive property of independent chi-square random variables.
To understand the steps involved in each of the proofs in the lesson.
To be able to apply the methods learned in the lesson to new problems.

25.1 - Uniqueness Property of M.G.F.s

Recall that the moment generating function:

$M_{X} (t) = E (e^{t X})$

uniquely defines the distribution of a random variable. That is, if you can show that the moment generating function of $\bar{X}$ is the same as some known moment-generating function, then $\bar{X}$ follows the same distribution. So, one strategy to finding the distribution of a function of random variables is:

To find the moment-generating function of the function of random variables
To compare the calculated moment-generating function to known moment-generating functions
If the calculated moment-generating function is the same as some known moment-generating function of $X$ , then the function of the random variables follows the same probability distribution as $X$

Example 25-1

In the previous lesson, we looked at an example that involved tossing a penny three times and letting $X_{1}$ denote the number of heads that we get in the three tosses. In the same example, we suggested tossing a second penny two times and letting $X_{2}$ denote the number of heads we get in those two tosses. We let:

$Y = X_{1} + X_{2}$

denote the number of heads in five tosses. What is the probability distribution of $Y$ ?

Solution

We know that:

$X_{1}$ is a binomial random variable with $n = 3$ and $p = \frac{1}{2}$
$X_{2}$ is a binomial random variable with $n = 2$ and $p = \frac{1}{2}$

Therefore, based on what we know of the moment-generating function of a binomial random variable, the moment-generating function of $X_{1}$ is:

$M_{X_{1}} (t) = {(\frac{1}{2} + \frac{1}{2} e^{t})}^{3}$

And, similarly, the moment-generating function of $X_{2}$ is:

$M_{X_{2}} (t) = {(\frac{1}{2} + \frac{1}{2} e^{t})}^{2}$

Now, because $X_{1}$ and $X_{2}$ are independent random variables, the random variable $Y$ is the sum of independent random variables. Therefore, the moment-generating function of $Y$ is:

$M_{Y} (t) = E (e^{t Y}) = E (e^{t (X_{1} + X_{2})}) = E (e^{t X_{1}} \cdot e^{t X_{2}}) = E (e^{t X_{1}}) \cdot E (e^{t X_{2}})$

The first equality comes from the definition of the moment-generating function of the random variable $Y$ . The second equality comes from the definition of $Y$ . The third equality comes from the properties of exponents. And, the fourth equality comes from the expectation of the product of functions of independent random variables. Now, substituting in the known moment-generating functions of $X_{1}$ and $X_{2}$ , we get:

$M_{Y} (t) = {(\frac{1}{2} + \frac{1}{2} e^{t})}^{3} \cdot {(\frac{1}{2} + \frac{1}{2} e^{t})}^{2} = {(\frac{1}{2} + \frac{1}{2} e^{t})}^{5}$

That is, $Y$ has the same moment-generating function as a binomial random variable with $n = 5$ and $p = \frac{1}{2}$ . Therefore, by the uniqueness properties of moment-generating functions, $Y$ must be a binomial random variable with $n = 5$ and $p = \frac{1}{2}$ . (Of course, we already knew that!)

It seems that we could generalize the way in which we calculated, in the above example, the moment-generating function of $Y$ , the sum of two independent random variables. Indeed, we can! On the next page!

25.2 - M.G.F.s of Linear Combinations

Theorem

If $X_{1}, X_{2}, \dots, X_{n}$ are $n$ independent random variables with respective moment-generating functions $M_{X_{i}} (t) = E (e^{t X_{i}})$ for $i = 1, 2, \dots, n$ , then the moment-generating function of the linear combination:

$Y = \sum_{i = 1}^{n} a_{i} X_{i}$

is:

$M_{Y} (t) = \prod_{i = 1}^{n} M_{X_{i}} (a_{i} t)$

Proof

The proof is very similar to the calculation we made in the example on the previous page. That is:

$\begin{aligned} M_{Y} (t) & = E [e^{t Y}] \\ = E [e^{t (a_{1} X_{1} + a_{2} X_{2} + \dots + a_{n} X_{n})}] \\ = E [e^{a_{1} t X_{1}}] E [e^{a_{2} t X_{2}}] \dots E [e^{a_{n} t X_{n}}] \\ = M_{X_{1}} (a_{1} t) M_{X_{2}} (a_{2} t) \dots M_{X_{n}} (a_{n} t) \\ = \prod_{i = 1}^{n} M_{X_{i}} (a_{i} t) \end{aligned}$

The first equality comes from the definition of the moment-generating function of the random variable $Y$ . The second equality comes from the given definition of $Y$ . The third equality comes from the properties of exponents, as well as from the expectation of the product of functions of independent random variables. The fourth equality comes from the definition of the moment-generating function of the random variables $X_{i}$ , for $i = 1, 2, \dots, n$ . And, the fifth equality comes from using product notation to write the product of the moment-generating functions.

While the theorem is useful in its own right, the following corollary is perhaps even more useful when dealing not just with independent random variables, but also random variables that are identically distributed — two characteristics that we get, of course, when we take a random sample.

Corollary

If $X_{1}, X_{2}, \dots, X_{n}$ are observations of a random sample from a population (distribution) with moment-generating function $M (t)$ , then:

The moment generating function of the linear combination $Y = \sum_{i = 1}^{n} X_{i}$ is $M_{Y} (t) = \prod_{i = 1}^{n} M (t) = [M (t)]^{n}$ .
The moment generating function of the sample mean $\bar{X} = \sum_{i = 1}^{n} (\frac{1}{n}) X_{i}$ is $M_{\bar{X}} (t) = \prod_{i = 1}^{n} M (\frac{t}{n}) = {[M (\frac{t}{n})]}^{n}$ .

Proof

use the preceding theorem with $a_{i} = 1$ for $i = 1, 2, \dots, n$
use the preceding theorem with $a_{i} = \frac{1}{n}$ for $i = 1, 2, \dots, n$

Example 25-2

Let $X_{1}, X_{2}$ , and $X_{3}$ denote a random sample of size 3 from a gamma distribution with $α = 7$ and $θ = 5$ . Let $Y$ be the sum of the three random variables:

$Y = X_{1} + X_{2} + X_{3}$

What is the distribution of $Y$ ?

Solution

The moment-generating function of a gamma random variable $X$ with $α = 7$ and $θ = 5$ is:

$M_{X} (t) = \frac{1}{(1 - 5 t)^{7}}$

for $t < \frac{1}{5}$ . Therefore, the corollary tells us that the moment-generating function of $Y$ is:

$M_{Y} (t) = [M_{X_{1}} (t)]^{3} = {(\frac{1}{(1 - 5 t)^{7}})}^{3} = \frac{1}{(1 - 5 t)^{21}}$

for $t < \frac{1}{5}$ , which is the moment-generating function of a gamma random variable with $α = 21$ and $θ = 5$ . Therefore, $Y$ must follow a gamma distribution with $α = 21$ and $θ = 5$ .

What is the distribution of the sample mean $\bar{X}$ ?

Solution

Again, the moment-generating function of a gamma random variable $X$ with $α = 7$ and $θ = 5$ is:

$M_{X} (t) = \frac{1}{(1 - 5 t)^{7}}$

for $t < \frac{1}{5}$ . Therefore, the corollary tells us that the moment-generating function of $\bar{X}$ is:

$M_{\bar{X}} (t) = {[M_{X_{1}} (\frac{t}{3})]}^{3} = {(\frac{1}{(1 - 5 (t / 3))^{7}})}^{3} = \frac{1}{(1 - (5 / 3) t)^{21}}$

for $t < \frac{3}{5}$ , which is the moment-generating function of a gamma random variable with $α = 21$ and $θ = \frac{5}{3}$ . Therefore, $\bar{X}$ must follow a gamma distribution with $α = 21$ and $θ = \frac{5}{3}$ .

25.3 - Sums of Chi-Square Random Variables

We'll now turn our attention towards applying the theorem and corollary of the previous page to the case in which we have a function involving a sum of independent chi-square random variables. The following theorem is often referred to as the "additive property of independent chi-squares."

Theorem

Let $X_{i}$ denote $n$ independent random variables that follow these chi-square distributions:

$X_{1} \sim χ^{2} (r_{1})$
$X_{2} \sim χ^{2} (r_{2})$
$⋮$
$X_{n} \sim χ^{2} (r_{n})$

Then, the sum of the random variables:

$Y = X_{1} + X_{2} + \dots + X_{n}$

follows a chi-square distribution with $r_{1} + r_{2} + \dots + r_{n}$ degrees of freedom. That is:

$Y \sim χ^{2} (r_{1} + r_{2} + \dots + r_{n})$

Proof

https://www.youtube.com/watch/Cb3b5gFqLRU ^[7]

We have shown that $M_{Y} (t)$ is the moment-generating function of a chi-square random variable with $r_{1} + r_{2} + \dots + r_{n}$ degrees of freedom. That is:

Y \sim χ^{2} (r_{1} + r_{2} + \dots + r_{n})

as was to be shown.

Theorem

Let $Z_{1}, Z_{2}, \dots, Z_{n}$ have standard normal distributions, $N (0, 1)$ . If these random variables are independent, then:

$W = Z_{1}^{2} + Z_{2}^{2} + \dots + Z_{n}^{2}$

follows a $χ^{2} (n)$ distribution.

Proof

Recall that if $Z_{i} \sim N (0, 1)$ , then $Z_{i}^{2} \sim χ^{2} (1)$ for $i = 1, 2, \dots, n$ . Then, by the additive property of independent chi-squares:

$W = Z_{1}^{2} + Z_{2}^{2} + \dots + Z_{n}^{2} \sim χ^{2} (1 + 1 + \dots + 1) = χ^{2} (n)$

That is, $W \sim χ^{2} (n)$ , as was to be proved.

Corollary

If $X_{1}, X_{2}, \dots, X_{n}$ are independent normal random variables with different means and variances, that is:

$X_{i} \sim N (μ_{i}, σ_{i}^{2})$

for $i = 1, 2, \dots, n$ . Then:

$W = \sum_{i = 1}^{n} \frac{(X_{i} - μ_{i})^{2}}{σ_{i}^{2}} \sim χ^{2} (n)$

Proof

Recall that:

$Z_{i} = \frac{(X_{i} - μ_{i})}{σ_{i}} \sim N (0, 1)$

Therefore:

$W = \sum_{i = 1}^{n} Z_{i}^{2} = \sum_{i = 1}^{n} \frac{(X_{i} - μ_{i})^{2}}{σ_{i}^{2}} \sim χ^{2} (n)$

as was to be proved.

Lesson 26: Random Functions Associated with Normal Distributions

Overview

In the previous lessons, we've been working our way up towards fully defining the probability distribution of the sample mean $\bar{X}$ and the sample variance $S^{2}$ . We have determined the expected value and variance of the sample mean. Now, in this lesson, we (finally) determine the probability distribution of the sample mean and sample variance when a random sample $X_{1}, X_{2}, \dots, X_{n}$ is taken from a normal population (distribution). We'll also learn about a new probability distribution called the (Student's) t distribution.

Objectives

Upon completion of this lesson, you should be able to:

To learn the probability distribution of a linear combination of independent normal random variables $X_{1}, X_{2}, \dots, X_{n}$ .
To learn how to find the probability that a linear combination of independent normal random variables $X_{1}, X_{2}, \dots, X_{n}$ takes on a certain interval of values.
To learn the sampling distribution of the sample mean when $X_{1}, X_{2}, \dots, X_{n}$ are a random sample from a normal population with mean $μ$ and variance $σ^{2}$ .
To use simulation to get a feel for the shape of a probability distribution.
To learn the sampling distribution of the sample variance when $X_{1}, X_{2}, \dots, X_{n}$ are a random sample from a normal population with mean $μ$ and variance $σ^{2}$ .
To learn the formal definition of a $T$ random variable.
To learn the characteristics of Student's $t$ distribution.
To learn how to read a $t$ -table to find $t$ -values and probabilities associated with $t$ -values.
To understand each of the steps in the proofs in the lesson.
To be able to apply the methods learned in this lesson to new problems.

26.1 - Sums of Independent Normal Random Variables

Well, we know that one of our goals for this lesson is to find the probability distribution of the sample mean when a random sample is taken from a population whose measurements are normally distributed. Then, let's just get right to the punch line! Well, first we'll work on the probability distribution of a linear combination of independent normal random variables $X_{1}, X_{2}, \dots, X_{n}$ . On the next page, we'll tackle the sample mean!

Theorem

If $X_{1}, X_{2}, \dots, X_{n}$ >are mutually independent normal random variables with means $μ_{1}, μ_{2}, \dots, μ_{n}$ and variances $σ_{1}^{2}, σ_{2}^{2}, \dots, σ_{n}^{2}$ , then the linear combination:

$Y = \sum_{i = 1}^{n} c_{i} X_{i}$

follows the normal distribution:

$N (\sum_{i = 1}^{n} c_{i} μ_{i}, \sum_{i = 1}^{n} c_{i}^{2} σ_{i}^{2})$

Proof

We'll use the moment-generating function technique to find the distribution of $Y$ . In the previous lesson, we learned that the moment-generating function of a linear combination of independent random variables $X_{1}, X_{2}, \dots, X_{n}$ >is:

$M_{Y} (t) = \prod_{i = 1}^{n} M_{X_{i}} (c_{i} t)$

Now, recall that if $X_{i} \sim N (μ, σ^{2})$ , then the moment-generating function of $X_{i}$ is:

$M_{X_{i}} (t) = exp (μ t + \frac{σ^{2} t^{2}}{2})$

Therefore, the moment-generating function of $Y$ is:

$M_{Y} (t) = \prod_{i = 1}^{n} M_{X_{i}} (c_{i} t) = \prod_{i = 1}^{n} exp [μ_{i} (c_{i} t) + \frac{σ_{i}^{2} (c_{i} t)^{2}}{2}]$

Evaluating the product at each index $i$ from 1 to $n$ , and using what we know about exponents, we get:

$M_{Y} (t) = exp (μ_{1} c_{1} t) \cdot exp (μ_{2} c_{2} t) \dots exp (μ_{n} c_{n} t) \cdot exp (\frac{σ_{1}^{2} c_{1}^{2} t^{2}}{2}) \cdot exp (\frac{σ_{2}^{2} c_{2}^{2} t^{2}}{2}) \dots exp (\frac{σ_{n}^{2} c_{n}^{2} t^{2}}{2})$

Again, using what we know about exponents, and rewriting what we have using summation notation, we get:

$M_{Y} (t) = exp [t (\sum_{i = 1}^{n} c_{i} μ_{i}) + \frac{t^{2}}{2} (\sum_{i = 1}^{n} c_{i}^{2} σ_{i}^{2})]$

Ahaaa! We have just shown that the moment-generating function of $Y$ is the same as the moment-generating function of a normal random variable with mean:

$\sum_{i = 1}^{n} c_{i} μ_{i}$

and variance:

$\sum_{i = 1}^{n} c_{i}^{2} σ_{i}^{2}$

Therefore, by the uniqueness property of moment-generating functions, $Y$ must be normally distributed with the said mean and said variance. Our proof is complete.

Example 26-1

Let $X_{1}$ be a normal random variable with mean 2 and variance 3, and let $X_{2}$ be a normal random variable with mean 1 and variance 4. Assume that $X_{1}$ and $X_{2}$ are independent. What is the distribution of the linear combination $Y = 2 X_{1} + 3 X_{2}$ ?

Solution

The previous theorem tells us that $Y$ is normally distributed with mean 7 and variance 48 as the following calculation illustrates:

$(2 X_{1} + 3 X_{2}) \sim N (2 (2) + 3 (1), 2^{2} (3) + 3^{2} (4)) = N (7, 48)$

What is the distribution of the linear combination $Y = X_{1} - X_{2}$ ?

Solution

The previous theorem tells us that $Y$ is normally distributed with mean 1 and variance 7 as the following calculation illustrates:

$(X_{1} - X_{2}) \sim N (2 - 1, (1)^{2} (3) + (- 1)^{2} (4)) = N (1, 7)$

Example 26-2

History suggests that scores on the Math portion of the Standard Achievement Test (SAT) are normally distributed with a mean of 529 and a variance of 5732. History also suggests that scores on the Verbal portion of the SAT are normally distributed with a mean of 474 and a variance of 6368. Select two students at random. Let $X$ denote the first student's Math score, and let $Y$ denote the second student's Verbal score. What is $P (X > Y)$ ?

Solution

We can find the requested probability by noting that $P (X > Y) = P (X - Y > 0)$ , and then taking advantage of what we know about the distribution of $X - Y$ . That is, $X - Y$ is normally distributed with a mean of 55 and variance of 12100 as the following calculation illustrates:

$(X - Y) \sim N (529 - 474, (1)^{2} (5732) + (- 1)^{2} (6368)) = N (55, 12100)$

Then, finding the probability that $X$ is greater than $Y$ reduces to a normal probability calculation:

$\begin{aligned} P (X > Y) & = P (X - Y > 0) \\ = P (Z > \frac{0 - 55}{\sqrt{12100}}) \\ = P (Z > - \frac{1}{2}) = P (Z < \frac{1}{2}) = 0.6915 \end{aligned}$

That is, the probability that the first student's Math score is greater than the second student's Verbal score is 0.6915.

Example 26-3

Let $X_{i}$ denote the weight of a randomly selected prepackaged one-pound bag of carrots. Of course, one-pound bags of carrots won't weigh exactly one pound. In fact, history suggests that $X_{i}$ is normally distributed with a mean of 1.18 pounds and a standard deviation of 0.07 pound.

Now, let $W$ denote the weight of randomly selected prepackaged three-pound bag of carrots. Three-pound bags of carrots won't weigh exactly three pounds either. In fact, history suggests that $W$ is normally distributed with a mean of 3.22 pounds and a standard deviation of 0.09 pound.

Selecting bags at random, what is the probability that the sum of three one-pound bags exceeds the weight of one three-pound bag?

Solution

Because the bags are selected at random, we can assume that $X_{1}, X_{2}, X_{3}$ and $W$ are mutually independent. The theorem helps us determine the distribution of $Y$ , the sum of three one-pound bags:

$Y = (X_{1} + X_{2} + X_{3}) \sim N (1.18 + 1.18 + 1.18, {0.07}^{2} + {0.07}^{2} + {0.07}^{2}) = N (3.54, 0.0147)$

That is, $Y$ is normally distributed with a mean of 3.54 pounds and a variance of 0.0147. Now, $Y - W$ , the difference in the weight of three one-pound bags and one three-pound bag is normally distributed with a mean of 0.32 and a variance of 0.0228, as the following calculation suggests:

$(Y - W) \sim N (3.54 - 3.22, (1)^{2} (0.0147) + (- 1)^{2} ({0.09}^{2})) = N (0.32, 0.0228)$

Therefore, finding the probability that $Y$ is greater than $W$ reduces to a normal probability calculation:

$\begin{aligned} P (Y > W) & = P (Y - W > 0) \\ = P (Z > \frac{0 - 0.32}{\sqrt{0.0228}}) \\ = P (Z > - 2.12) = P (Z < 2.12) = 0.9830 \end{aligned}$

That is, the probability that the sum of three one-pound bags exceeds the weight of one three-pound bag is 0.9830. Hey, if you want more bang for your buck, it looks like you should buy multiple one-pound bags of carrots, as opposed to one three-pound bag!

26.2 - Sampling Distribution of Sample Mean

Okay, we finally tackle the probability distribution (also known as the "sampling distribution") of the sample mean when $X_{1}, X_{2}, \dots, X_{n}$ are a random sample from a normal population with mean $μ$ and variance $σ^{2}$ . The word "tackle" is probably not the right choice of word, because the result follows quite easily from the previous theorem, as stated in the following corollary.

Corollary

If $X_{1}, X_{2}, \dots, X_{n}$ are observations of a random sample of size $n$ from a $N (μ, σ^{2})$ population, then the sample mean:

$\bar{X} = \frac{1}{n} \sum_{i = 1}^{n} X_{i}$

is normally distributed with mean $μ$ and variance $\frac{σ^{2}}{n}$ . That is, the probability distribution of the sample mean is:

$N (μ, σ^{2} / n)$

Proof

The result follows directly from the previous theorem. All we need to do is recognize that the sample mean:

$\bar{X} = \frac{X_{1} + X_{2} + \dots + X_{n}}{n}$

is a linear combination of independent normal random variables:

$\bar{X} = \frac{1}{n} X_{1} + \frac{1}{n} X_{2} + \dots + \frac{1}{n} X_{n}$

with $c_{i} = \frac{1}{n}$ , the mean $μ_{i} = μ$ and the variance $σ_{i}^{2} = σ^{2}$ . That is, the moment generating function of the sample mean is then:

$M_{\bar{X}} (t) = exp [t (\sum_{i = 1}^{n} c_{i} μ_{i}) + \frac{t^{2}}{2} (\sum_{i = 1}^{n} c_{i}^{2} σ_{i}^{2})] = exp [t (\sum_{i = 1}^{n} \frac{1}{n} μ) + \frac{t^{2}}{2} (\sum_{i = 1}^{n} {(\frac{1}{n})}^{2} σ^{2})]$

The first equality comes from the theorem on the previous page, about the distribution of a linear combination of independent normal random variables. The second equality comes from simply replacing $c_{i}$ with $\frac{1}{n}$ , the mean $μ_{i}$ with $μ$ and the variance $σ_{i}^{2}$ with $σ^{2}$ . Now, working on the summations, the moment generating function of the sample mean reduces to:

$M_{\bar{X}} (t) = exp [t (\frac{1}{n} \sum_{i = 1}^{n} μ) + \frac{t^{2}}{2} (\frac{1}{n^{2}} \sum_{i = 1}^{n} σ^{2})] = exp [t (\frac{1}{n} (n μ)) + \frac{t^{2}}{2} (\frac{1}{n^{2}} (n σ^{2}))] = exp [μ t + \frac{t^{2}}{2} (\frac{σ^{2}}{n})]$

The first equality comes from pulling the constants depending on $n$ through the summation signs. The second equality comes from adding $μ$ up $n$ times to get $n μ$ , and adding $σ^{2}$ up $n$ times to get $n σ^{2}$ . The last equality comes from simplifying a bit more. In summary, we have shown that the moment generating function of the sample mean of $n$ independent normal random variables with mean $μ$ and variance $σ^{2}$ is:

$M_{\bar{X}} (t) = exp [μ t + \frac{t^{2}}{2} (\frac{σ^{2}}{n})]$

That is the same as the moment generating function of a normal random variable with mean $μ$ and variance $\frac{σ^{2}}{n}$ . Therefore, the uniqueness property of moment-generating functions tells us that the sample mean must be normally distributed with mean $μ$ and variance $\frac{σ^{2}}{n}$ . Our proof is complete.

Example 26-4

Let $X_{i}$ denote the Stanford-Binet Intelligence Quotient (IQ) of a randomly selected individual, $i = 1, \dots, 4$ (one sample). Let $Y_{i}$ denote the IQ of a randomly selected individual, $i = 1, \dots, 8$ (a second sample). Recalling that IQs are normally distributed with mean $μ = 100$ and variance $σ^{2} = 16^{2}$ , what is the distribution of $\bar{X}$ ? And, what is the distribution of $\bar{Y}$ ?

Anwser

In general, the variance of the sample mean is:

$V a r (\bar{X}) = \frac{σ^{2}}{n}$

Therefore, the variance of the sample mean of the first sample is:

$V a r ({\bar{X}}_{4}) = \frac{16^{2}}{4} = 64$

(The subscript 4 is there just to remind us that the sample mean is based on a sample of size 4.) And, the variance of the sample mean of the second sample is:

$V a r ({\bar{Y}}_{8} = \frac{16^{2}}{8} = 32$

(The subscript 8 is there just to remind us that the sample mean is based on a sample of size 8.) Now, the corollary therefore tells us that the sample mean of the first sample is normally distributed with mean 100 and variance 64. That is:

${\bar{X}}_{4} \sim N (100, 64)$

And, the sample mean of the second sample is normally distributed with mean 100 and variance 32. That is:

${\bar{Y}}_{8} \sim N (100, 32)$

So, we have two, no actually, three normal random variables with the same mean, but difference variances:

We have $X_{i}$ , an IQ of a random individual. It is normally distributed with mean 100 and variance 256.
We have ${\bar{X}}_{4}$ , the average IQ of 4 random individuals. It is normally distributed with mean 100 and variance 64.
We have ${\bar{Y}}_{8}$ , the average IQ of 8 random individuals. It is normally distributed with mean 100 and variance 32.

It is quite informative to graph these three distributions on the same plot. Doing so, we get:

As the plot suggests, an individual $X_{i}$ , the mean (\bar{X}_4\) and the mean ${\bar{Y}}_{8}$ all provide valid, "unbiased" estimates of the population mean $μ$ . But, our intuition coincides with reality... that is, the sample mean ${\bar{Y}}_{8}$ will be the most precise estimate of $μ$ .

All the work that we have done so far concerning this example has been theoretical in nature. That is, what we have learned is based on probability theory. Would we see the same kind of result if we were take to a large number of samples, say 1000, of size 4 and 8, and calculate the sample mean of each sample? That is, would the distribution of the 1000 sample means based on a sample of size 4 look like a normal distribution with mean 100 and variance 64? And would the distribution of the 1000 sample means based on a sample of size 8 look like a normal distribution with mean 100 and variance 32? Well, the only way to answer these questions is to try it out!

I did just that for us. I used Minitab to generate 1000 samples of eight random numbers from a normal distribution with mean 100 and variance 256. Here's a subset of the resulting random numbers:

ROW	X1	X2	X3	X4	X5	X6	X7	X8	Mean 4	Mean 8
1	87	68	98	114	59	111	114	86	91.75	92.125
2	102	81	74	110	112	106	105	99	91.75	98.625
3	96	87	50	88	69	107	94	83	80.25	84.250
4	83	134	122	80	117	110	115	158	104.75	114.875
5	92	87	120	93	90	111	95	92	98.00	97.500
6	139	102	100	103	111	62	78	73	111.00	96.000
7	134	121	99	118	108	106	103	91	118.00	110.000
8	126	92	148	131	99	106	143	128	124.25	121.625
9	98	109	119	110	124	99	119	82	109.00	107.500
10	85	93	82	106	93	109	100	95	91.50	95.375
11	121	103	108	96	112	117	93	112	107.00	107.750
12	118	91	106	108	128	96	65	85	105.75	99.625
13	92	87	96	81	86	105	91	104	89.00	92.750
14	94	115	59	105	101	122	97	103	93.25	99.500

...and so on...

975	108	139	130	97	138	88	104	87	118.50	111.375
976	99	122	93	107	98	62	102	115	105.25	99.750
977	99	127	91	101	127	79	81	121	104.50	103.250
978	120	108	101	104	90	90	191	104	108.25	101.000
979	101	93	106	113	115	82	96	97	103.25	100.375
980	118	86	74	95	109	111	90	83	93.25	95.750
981	118	95	121	124	111	90	105	112	114.50	109.500
982	110	121	85	117	91	84	84	108	108.25	100.000
983	95	109	118	112	121	105	84	115	108.50	107.375
984	102	105	127	104	95	101	106	103	109.50	105.375
985	116	93	112	102	67	92	103	114	105.75	99.875
986	106	97	114	82	82	108	113	81	99.75	97.875
987	107	93	78	91	83	81	115	102	92.25	93.750
988	106	115	105	74	86	124	97	116	100.00	102.875
989	117	84	131	102	92	118	90	90	108.50	103.000
990	100	69	108	128	111	110	94	95	101.25	101.875
991	86	85	123	94	104	89	76	97	97.00	94.250
992	94	90	72	121	105	150	72	88	94.25	99.000
993	70	109	104	114	93	103	126	99	99.25	102.250
994	102	110	98	93	64	131	91	95	100.75	98.000
995	80	135	120	92	118	119	66	117	106.75	105.875
996	81	102	88	98	113	81	95	110	92.25	96.000
997	85	146	73	133	111	88	92	74	109.25	100.250
998	94	109	110	115	95	93	90	103	107.00	101.125
999	84	84	97	125	92	89	95	124	97.50	98.750
1000	77	60	113	106	107	109	110	103	89.00	98.125

As you can see, the second last column, titled Mean4, is the average of the first four columns X1 X2, X3, and X4. The last column, titled Mean8, is the average of the first eight columns X1, X2, X3, X4, X5, X6, X7, and X8. Now, all we have to do is create a histogram of the sample means appearing in the Mean4 column:

Ahhhh! The histogram sure looks fairly bell-shaped, making the normal distribution a real possibility. Now, recall that the Empirical Rule tells us that we should expect, if the sample means are normally distributed, that almost all of the sample means would fall within three standard deviations of the population mean. That is, in the case of Mean4, we should expect almost all of the data to fall between 76 (from 100−3(8)) and 124 (from 100+3(8)). It sure looks like that's the case!

Let's do the same thing for the Mean8 column. That is, let's create a histogram of the sample means appearing in the Mean8 column. Doing so, we get:

Again, the histogram sure looks fairly bell-shaped, making the normal distribution a real possibility. In this case, the Empirical Rule tells us that, in the case of Mean8, we should expect almost all of the data to fall between 83 (from 100−3(square root of 32)) and 117 (from 100+3(square root of 32)). It too looks pretty good on both sides, although it seems that there were two really extreme sample means of size 8. (If you look back at the data, you can see one of them in the eighth row.)

In summary, the whole point of this exercise was to use the theory to help us derive the distribution of the sample mean of IQs, and then to use real simulated normal data to see if our theory worked in practice. I think we can conclude that it does!

26.3 - Sampling Distribution of Sample Variance

Now that we've got the sampling distribution of the sample mean down, let's turn our attention to finding the sampling distribution of the sample variance. The following theorem will do the trick for us!

Theorem

$X_{1}, X_{2}, \dots, X_{n}$ are observations of a random sample of size $n$ from the normal distribution $N (μ, σ^{2})$
$\bar{X} = \frac{1}{n} \sum_{i = 1}^{n} X_{i}$ is the sample mean of the $n$ observations, and
$S^{2} = \frac{1}{n - 1} \sum_{i = 1}^{n} (X_{i} - \bar{X})^{2}$ is the sample variance of the $n$ observations.

Then:

$\bar{X}$ and $S^{2}$ are independent
$\frac{(n - 1) S^{2}}{σ^{2}} = \frac{\sum_{i = 1}^{n} (X_{i} - \bar{X})^{2}}{σ^{2}} \sim χ^{2} (n - 1)$

Proof

The proof of number 1 is quite easy. Errr, actually not! It is quite easy in this course, because it is beyond the scope of the course. So, we'll just have to state it without proof.

Now for proving number 2. This is one of those proofs that you might have to read through twice... perhaps reading it the first time just to see where we're going with it, and then, if necessary, reading it again to capture the details. We're going to start with a function which we'll call $W$ :

$W = \sum_{i = 1}^{n} {(\frac{X_{i} - μ}{σ})}^{2}$

Now, we can take $W$ and do the trick of adding 0 to each term in the summation. Doing so, of course, doesn't change the value of $W$ :

$W = \sum_{i = 1}^{n} {(\frac{(X_{i} - \bar{X}) + (\bar{X} - μ)}{σ})}^{2}$

As you can see, we added 0 by adding and subtracting the sample mean to the quantity in the numerator. Now, let's square the term. Doing just that, and distributing the summation, we get:

$W = \sum_{i = 1}^{n} {(\frac{X_{i} - \bar{X}}{σ})}^{2} + \sum_{i = 1}^{n} {(\frac{\bar{X} - μ}{σ})}^{2} + 2 (\frac{\bar{X} - μ}{σ^{2}}) \sum_{i = 1}^{n} (X_{i} - \bar{X})$

But the last term is 0:

$W = \sum_{i = 1}^{n} {(\frac{X_{i} - \bar{X}}{σ})}^{2} + \sum_{i = 1}^{n} {(\frac{\bar{X} - μ}{σ})}^{2} + \underset{0, s i n c e \sum (X_{i} - \bar{X}) = n \bar{X} - n \bar{X} = 0}{\underset{⏟}{2 (\frac{\bar{X} - μ}{σ^{2}}) \sum_{i = 1}^{n} (X_{i} - \bar{X})}}$

so, $W$ reduces to:

$W = \sum_{i = 1}^{n} \frac{(X_{i} - \bar{X})^{2}}{σ^{2}} + \frac{n (\bar{X} - μ)^{2}}{σ^{2}}$

We can do a bit more with the first term of $W$ . As an aside, if we take the definition of the sample variance:

$S^{2} = \frac{1}{n - 1} \sum_{i = 1}^{n} (X_{i} - \bar{X})^{2}$

and multiply both sides by $(n - 1)$ , we get:

$(n - 1) S^{2} = \sum_{i = 1}^{n} (X_{i} - \bar{X})^{2}$

So, the numerator in the first term of $W$ can be written as a function of the sample variance. That is:

$W = \sum_{i = 1}^{n} {(\frac{X_{i} - μ}{σ})}^{2} = \frac{(n - 1) S^{2}}{σ^{2}} + \frac{n (\bar{X} - μ)^{2}}{σ^{2}}$

Okay, let's take a break here to see what we have. We've taken the quantity on the left side of the above equation, added 0 to it, and showed that it equals the quantity on the right side. Now, what can we say about each of the terms. Well, the term on the left side of the equation:

$\sum_{i = 1}^{n} {(\frac{X_{i} - μ}{σ})}^{2}$

is a sum of $n$ independent chi-square(1) random variables. That's because we have assumed that $X_{1}, X_{2}, \dots, X_{n}$ are observations of a random sample of size $n$ from the normal distribution $N (μ, σ^{2})$ . Therefore:

$\frac{X_{i} - μ}{σ}$

follows a standard normal distribution. Now, recall that if we square a standard normal random variable, we get a chi-square random variable with 1 degree of freedom. So, again:

$\sum_{i = 1}^{n} {(\frac{X_{i} - μ}{σ})}^{2}$

is a sum of $n$ independent chi-square(1) random variables. Our work from the previous lesson then tells us that the sum is a chi-square random variable with $n$ degrees of freedom. Therefore, the moment-generating function of $W$ is the same as the moment-generating function of a chi-square(n) random variable, namely:

$M_{W} (t) = (1 - 2 t)^{- n / 2}$

for $t < \frac{1}{2}$ . Now, the second term of $W$ , on the right side of the equals sign, that is:

$\frac{n (\bar{X} - μ)^{2}}{σ^{2}}$

is a chi-square(1) random variable. That's because the sample mean is normally distributed with mean $μ$ and variance $\frac{σ^{2}}{n}$ . Therefore:

$Z = \frac{\bar{X} - μ}{σ / \sqrt{n}} \sim N (0, 1)$

is a standard normal random variable. So, if we square $Z$ , we get a chi-square random variable with 1 degree of freedom:

$Z^{2} = \frac{n (\bar{X} - μ)^{2}}{σ^{2}} \sim χ^{2} (1)$

And therefore the moment-generating function of $Z^{2}$ is:

$M_{Z^{2}} (t) = (1 - 2 t)^{- 1 / 2}$

for $t < \frac{1}{2}$ . Let's summarize again what we know so far. $W$ is a chi-square(n) random variable, and the second term on the right is a chi-square(1) random variable:

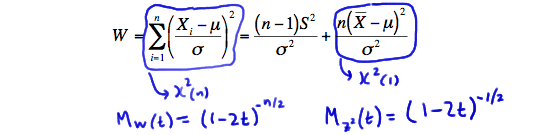
Now, let's use the uniqueness property of moment-generating functions. By definition, the moment-generating function of $W$ is:

$M_{W} (t) = E (e^{t W}) = E [e^{t ((n - 1) S^{2} / σ^{2} + Z^{2})}]$

Using what we know about exponents, we can rewrite the term in the expectation as a product of two exponent terms:

$E (e^{t W}) = E [e^{t ((n - 1) S^{2} / σ^{2})} \cdot e^{t Z^{2}}] = M_{(n - 1) S^{2} / σ^{2}} (t) \cdot M_{Z^{2}} (t)$

The last equality in the above equation comes from the independence between $\bar{X}$ and $S^{2}$ . That is, if they are independent, then functions of them are independent. Now, let's substitute in what we know about the moment-generating function of $W$ and of $Z^{2}$ . Doing so, we get:

$(1 - 2 t)^{- n / 2} = M_{(n - 1) S^{2} / σ^{2}} (t) \cdot (1 - 2 t)^{- 1 / 2}$

Now, let's solve for the moment-generating function of $\frac{(n - 1) S^{2}}{σ^{2}}$ , whose distribution we are trying to determine. Doing so, we get:

$M_{(n - 1) S^{2} / σ^{2}} (t) = (1 - 2 t)^{- n / 2} \cdot (1 - 2 t)^{1 / 2}$

Adding the exponents, we get:

$M_{(n - 1) S^{2} / σ^{2}} (t) = (1 - 2 t)^{- (n - 1) / 2}$

for $t < \frac{1}{2}$ . But, oh, that's the moment-generating function of a chi-square random variable with $n - 1$ degrees of freedom. Therefore, the uniqueness property of moment-generating functions tells us that $\frac{(n - 1) S^{2}}{σ^{2}}$ must be a a chi-square random variable with $n - 1$ degrees of freedom. That is:

$\frac{(n - 1) S^{2}}{σ^{2}} = \frac{\sum_{i = 1}^{n} (X_{i} - \bar{X})^{2}}{σ^{2}} \sim χ_{(n - 1)}^{2}$

as was to be proved! And, to just think that this was the easier of the two proofs

Before we take a look at an example involving simulation, it is worth noting that in the last proof, we proved that, when sampling from a normal distribution:

$\frac{\sum_{i = 1}^{n} (X_{i} - μ)^{2}}{σ^{2}} \sim χ^{2} (n)$

but:

$\frac{\sum_{i = 1}^{n} (X_{i} - \bar{X})^{2}}{σ^{2}} = \frac{(n - 1) S^{2}}{σ^{2}} \sim χ^{2} (n - 1)$

The only difference between these two summations is that in the first case, we are summing the squared differences from the population mean $μ$ , while in the second case, we are summing the squared differences from the sample mean $\bar{X}$ . What happens is that when we estimate the unknown population mean $μ$ with $\bar{X}$ we "lose" one degreee of freedom. This is generally true... a degree of freedom is lost for each parameter estimated in certain chi-square random variables.

Example 26-5

Let's return to our example concerning the IQs of randomly selected individuals. Let $X_{i}$ denote the Stanford-Binet Intelligence Quotient (IQ) of a randomly selected individual, $i = 1, \dots, 8$ . Recalling that IQs are normally distributed with mean $μ = 100$ and variance $σ^{2} = 16^{2}$ , what is the distribution of $\frac{(n - 1) S^{2}}{σ^{2}}$ ?

Solution

Because the sample size is $n = 8$ , the above theorem tells us that:

$\frac{(8 - 1) S^{2}}{σ^{2}} = \frac{7 S^{2}}{σ^{2}} = \frac{\sum_{i = 1}^{8} (X_{i} - \bar{X})^{2}}{σ^{2}}$

follows a chi-square distribution with 7 degrees of freedom. Here's what the theoretical density function would look like:

Again, all the work that we have done so far concerning this example has been theoretical in nature. That is, what we have learned is based on probability theory. Would we see the same kind of result if we were take to a large number of samples, say 1000, of size 8, and calculate:

$\frac{\sum_{i = 1}^{8} (X_{i} - \bar{X})^{2}}{256}$

for each sample? That is, would the distribution of the 1000 resulting values of the above function look like a chi-square(7) distribution? Again, the only way to answer this question is to try it out! I did just that for us. I used Minitab to generate 1000 samples of eight random numbers from a normal distribution with mean 100 and variance 256. Here's a subset of the resulting random numbers:

data
click to enlarge ^[8]

As you can see, the last column, titled FnofSsq (for function of sums of squares), contains the calculated value of:

$\frac{\sum_{i = 1}^{8} (X_{i} - \bar{X})^{2}}{256}$

based on the random numbers generated in columns X1 X2, X3, X4, X5, X6, X7, and X8. For example, given that the average of the eight numbers in the first row is 98.625, the value of FnofSsq in the first row is:

$\frac{1}{256} [(98 - 98.625)^{2} + (77 - 98.625)^{2} + \dots + (91 - 98.625)^{2}] = 5.7651$

Now, all we have to do is create a histogram of the values appearing in the FnofSsq column. Doing so, we get:

Hmm! The histogram sure looks eerily similar to that of the density curve of a chi-square random variable with 7 degrees of freedom. It looks like the practice is meshing with the theory!

26.4 - Student's t Distribution

We have just one more topic to tackle in this lesson, namely, Student's t distribution. Let's just jump right in and define it!

Definition. If $Z \sim N (0, 1)$ and $U \sim χ^{2} (r)$ are independent, then the random variable:

$T = \frac{Z}{\sqrt{U / r}}$

follows a $t$ -distribution with $r$ degrees of freedom. We write $T \sim t (r)$ . The p.d.f. of T is:

$f (t) = \frac{Γ ((r + 1) / 2)}{\sqrt{π r} Γ (r / 2)} \cdot \frac{1}{(1 + t^{2} / r)^{(r + 1) / 2}}$

for $- \infty < t < \infty$ .

By the way, the $t$ distribution was first discovered by a man named W.S. Gosset. He discovered the distribution when working for an Irish brewery. Because he published under the pseudonym Student, the $t$ distribution is often called Student's $t$ distribution.

History aside, the above definition is probably not particularly enlightening. Let's try to get a feel for the $t$ distribution by way of simulation. Let's randomly generate 1000 standard normal values ( $Z$ ) and 1000 chi-square(3) values ( $U$ ). Then, the above definition tells us that, if we take those randomly generated values, calculate:

$T = \frac{Z}{\sqrt{U / 3}}$

and create a histogram of the 1000 resulting $T$ values, we should get a histogram that looks like a $t$ distribution with 3 degrees of freedom. Well, here's a subset of the resulting values from one such simulation:

ROW	Z	CHISQ (3)	T(3)
1	-2.60481	10.2497	-1.4092
2	2.92321	1.6517	3.9396
3	-0.48633	0.1757	-2.0099
4	-0.48212	3.8283	-0.4268
5	-0.04150	0.2422	-0.1461
6	-0.84225	-0.0903	-4.8544
7	-0.31205	1.6326	-0.4230
8	1.33068	5.2224	1.0086
9	-0.64104	0.9401	-1.1451
10	-0.05110	2.2632	-0.0588
11	1.61601	4.6566	1.2971
12	0.81522	2.1738	0.9577
13	0.38501	1.8404	0.4916
14	-1.63426	1.1265	-2.6669

...and so on...

994	-0.18942	3.5202	-0.1749
995	0.43078	3.3585	0.4071
996	-0.14068	0.6236	-0.3085
997	-1.76357	2.6188	-1.8876
998	-1.02310	3.2470	-0.9843
999	-0.93777	1.4991	-1.3266
1000	-0.37665	2.1231	-0.4477

Note, for example, in the first row:

$T (3) = \frac{- 2.60481}{\sqrt{10.2497 / 3}} = - 1.4092$

Here's what the resulting histogram of the 1000 randomly generated $T (3)$ values looks like, with a standard $N (0, 1)$ curve superimposed:

Hmmm. The $t$ -distribution seems to be quite similar to the standard normal distribution. Using the formula given above for the p.d.f. of $T$ , we can plot the density curve of various $t$ random variables, say when $r = 1, r = 4$ , and $r = 7$ , to see that that is indeed the case:

In fact, it looks as if, as the degrees of freedom $r$ increases, the $t$ density curve gets closer and closer to the standard normal curve. Let's summarize what we've learned in our little investigation about the characteristics of the t distribution:

The support appears to be $- \infty < t < \infty$ . (It is!)
The probability distribution appears to be symmetric about $t = 0$ . (It is!)
The probability distribution appears to be bell-shaped. (It is!)
The density curve looks like a standard normal curve, but the tails of the $t$ -distribution are "heavier" than the tails of the normal distribution. That is, we are more likely to get extreme $t$ -values than extreme $z$ -values.
As the degrees of freedom $r$ increases, the $t$ -distribution appears to approach the standard normal $z$ -distribution. (It does!)

As you'll soon see, we'll need to look up $t$ -values, as well as probabilities concerning $T$ random variables, quite often in Stat 415. Therefore, we better make sure we know how to read a $t$ table.

The $t$ Table

If you take a look at Table VI in the back of your textbook, you'll find what looks like a typical $t$ table. Here's what the top of Table VI looks like (well, minus the shading that I've added):

$P (T \leq t) = \int_{- \infty}^{t} \frac{Γ [(r + 1) / 2]}{\sqrt{π r} Γ (r / 2) {(1 + w^{2} / r)}^{(r + 1) / 2}} d w$

$P (T \leq - t) = 1 - P (T \leq t)$

P(T≤ t)
	0.60	0.75	0.90	0.95	0.975	0.99	0.995
r	^t_0.40(r)	^t_0.25(r)	^t_0.10(r)	^t_0.05(r)	^t_0.025(r)	^t_0.01(r)	^t_0.005(r)
1	0.325	1.000	3.078	6.314	12.706	31.821	63.657
2	0.289	0.816	1.886	2.920	4.303	6.965	9.925
3	0.277	0.765	1.638	2.353	3.182	4.541	5.841
4	0.271	0.741	1.533	2.132	2.776	3.747	4.604
5	0.267	0.727	1.476	2.015	2.571	3.365	4.032

6	0.265	0.718	1.440	1.943	2.447	3.143	3.707
7	0.263	0.711	1.415	1.895	2.365	2.998	3.499
8	0.262	0.706	1.397	1.860	2.306	2.896	3.355
9	0.261	0.703	1.383	1.833	2.262	2.821	3.250
10	0.260	0.700	1.372	1.812	2.228	2.764	3.169

The $t$ -table is similar to the chi-square table in that the inside of the $t$ -table (shaded in purple) contains the $t$ -values for various cumulative probabilities (shaded in red), such as 0.60, 0.75, 0.90, 0.95, 0.975, 0.99, and 0.995, and for various $t$ distributions with $r$ degrees of freedom (shaded in blue). The row shaded in green indicates the upper $α$ probability that corresponds to the $1 - α$ cumulative probability. For example, if you're interested in either a cumulative probability of 0.60, or an upper probability of 0.40, you'll want to look for the $t$ -value in the first column.

Let's use the $t$ -table to read a few probabilities and $t$ -values off of the table:

https://www.youtube.com/watch/pG546F9IAXw ^[9]

Let's take a look at a few more examples.

Example 26-6

Let $T$ follow a $t$ -distribution with $r = 8$ df. What is the probability that the absolute value of $T$ is less than 2.306?

Solution

The probability calculation is quite similar to a calculation we'd have to make for a normal random variable. First, rewriting the probability in terms of $T$ instead of the absolute value of $T$ , we get:

$P (| T | < 2.306) = P (- 2.306 < T < 2.306)$

Then, we have to rewrite the probability in terms of cumulative probabilities that we can actually find, that is:

$P (| T | < 2.306) = P (T < 2.306) - P (T < - 2.306)$

Pictorially, the probability we are looking for looks something like this:

But the $t$ -table doesn't contain negative $t$ -values, so we'll have to take advantage of the symmetry of the $T$ distribution. That is:

> $P (| T | < 2.306) = P (T < 2.306) - P (T > 2.306)$

Can you find the necessary

t

-values on the

t

-table?

P(T≤ t)
	0.60	0.75	0.90	0.95	0.975	0.99	0.995
r	^t_0.40(r)	^t_0.25(r)	^t_0.10(r)	^t_0.05(r)	^t_0.025(r)	^t_0.01(r)	^t_0.005(r)
1	0.325	1.000	3.078	6.314	12.706	31.821	63.657
2	0.289	0.816	1.886	2.920	4.303	6.965	9.925
3	0.277	0.765	1.638	2.353	3.182	4.541	5.841
4	0.271	0.741	1.533	2.132	2.776	3.747	4.604
5	0.267	0.727	1.476	2.015	2.571	3.365	4.032

6	0.265	0.718	1.440	1.943	2.447	3.143	3.707
7	0.263	0.711	1.415	1.895	2.365	2.998	3.499
8	0.262	0.706	1.397	1.860	2.306	2.896	3.355
9	0.261	0.703	1.383	1.833	2.262	2.821	3.250
10	0.260	0.700	1.372	1.812	2.228	2.764	3.169

P(T≤ t)
	0.60	0.75	0.90	0.95	0.975	0.99	0.995
r	^t_0.40(r)	^t_0.25(r)	^t_0.10(r)	^t_0.05(r)	^t_0.025(r)	^t_0.01(r)	^t_0.005(r)
1	0.325	1.000	3.078	6.314	12.706	31.821	63.657
2	0.289	0.816	1.886	2.920	4.303	6.965	9.925
3	0.277	0.765	1.638	2.353	3.182	4.541	5.841
4	0.271	0.741	1.533	2.132	2.776	3.747	4.604
5	0.267	0.727	1.476	2.015	2.571	3.365	4.032

6	0.265	0.718	1.440	1.943	2.447	3.143	3.707
7	0.263	0.711	1.415	1.895	2.365	2.998	3.499
8	0.262	0.706	1.397	1.860	2.306	2.896	3.355
9	0.261	0.703	1.383	1.833	2.262	2.821	3.250
10	0.260	0.700	1.372	1.812	2.228	2.764	3.169

The $t$ -table tells us that $P (T < 2.306) = 0.975$ and $P (T > 2.306) = 0.025$ . Therefore:

$P (| T | > 2.306) = 0.975 - 0.025 = 0.95$

What is $t_{0.05} (8)$ ?

Solution

The value $t_{0.05} (8)$ is the value $t_{0.05}$ such that the probability that a $T$ random variable with 8 degrees of freedom is greater than the value $t_{0.05}$ is 0.05. That is:

Can you find the value $t_{0.05}$ on the $t$ -table?

P(T≤ t)
	0.60	0.75	0.90	0.95	0.975	0.99	0.995
r	^t_0.40(r)	^t_0.25(r)	^t_0.10(r)	^t_0.05(r)	^t_0.025(r)	^t_0.01(r)	^t_0.005(r)
1	0.325	1.000	3.078	6.314	12.706	31.821	63.657
2	0.289	0.816	1.886	2.920	4.303	6.965	9.925
3	0.277	0.765	1.638	2.353	3.182	4.541	5.841
4	0.271	0.741	1.533	2.132	2.776	3.747	4.604
5	0.267	0.727	1.476	2.015	2.571	3.365	4.032

6	0.265	0.718	1.440	1.943	2.447	3.143	3.707
7	0.263	0.711	1.415	1.895	2.365	2.998	3.499
8	0.262	0.706	1.397	1.860	2.306	2.896	3.355
9	0.261	0.703	1.383	1.833	2.262	2.821	3.250
10	0.260	0.700	1.372	1.812	2.228	2.764	3.169

P(T≤ t)
	0.60	0.75	0.90	0.95	0.975	0.99	0.995
r	^t_0.40(r)	^t_0.25(r)	^t_0.10(r)	^t_0.05(r)	^t_0.025(r)	^t_0.01(r)	^t_0.005(r)
1	0.325	1.000	3.078	6.314	12.706	31.821	63.657
2	0.289	0.816	1.886	2.920	4.303	6.965	9.925
3	0.277	0.765	1.638	2.353	3.182	4.541	5.841
4	0.271	0.741	1.533	2.132	2.776	3.747	4.604
5	0.267	0.727	1.476	2.015	2.571	3.365	4.032

6	0.265	0.718	1.440	1.943	2.447	3.143	3.707
7	0.263	0.711	1.415	1.895	2.365	2.998	3.499
8	0.262	0.706	1.397	1.860	2.306	2.896	3.355
9	0.261	0.703	1.383	1.833	2.262	2.821	3.250
10	0.260	0.700	1.372	1.812	2.228	2.764	3.169

We have determined that the probability that a $T$ random variable with 8 degrees of freedom is greater than the value 1.860 is 0.05.

Why will we encounter a $T$ random variable?

Given a random sample $X_{1}, X_{2}, \dots, X_{n}$ from a normal distribution, we know that:

$Z = \frac{\bar{X} - μ}{σ / \sqrt{n}} \sim N (0, 1)$

Earlier in this lesson, we learned that:

$U = \frac{(n - 1) S^{2}}{σ^{2}}$

follows a chi-square distribution with $n - 1$ degrees of freedom. We also learned that $Z$ and $U$ are independent. Therefore, using the definition of a $T$ random variable, we get:

https://www.youtube.com/watch/-TcPqa9J8SY ^[10]

It is the resulting quantity, that is:

$T = \frac{\bar{X} - μ}{s / \sqrt{n}}$

that will help us, in Stat 415, to use a mean from a random sample, that is $\bar{X}$ , to learn, with confidence, something about the population mean $μ$ .

Lesson 27: The Central Limit Theorem

Introduction

In the previous lesson, we investigated the probability distribution ("sampling distribution") of the sample mean when the random sample $X_{1}, X_{2}, \dots, X_{n}$ comes from a normal population with mean $μ$ and variance $σ^{2}$ , that is, when $X_{i} \sim N (μ, σ^{2}), i = 1, 2, \dots, n$ . Specifically, we learned that if $X_{i}$ , $i = 1, 2, \dots, n$ , is a random sample of size $n$ from a $N (μ, σ^{2})$ population, then:

$\bar{X} \sim N (μ, \frac{σ^{2}}{n})$

But what happens if the $X_{i}$ follow some other non-normal distribution? For example, what distribution does the sample mean follow if the $X_{i}$ come from the Uniform(0, 1) distribution? Or, what distribution does the sample mean follow if the $X_{i}$ come from a chi-square distribution with three degrees of freedom? Those are the kinds of questions we'll investigate in this lesson. As the title of this lesson suggests, it is the Central Limit Theorem that will give us the answer.

Objectives

Upon completion of this lesson, you should be able to:

To learn the Central Limit Theorem.
To get an intuitive feeling for the Central Limit Theorem.
To use the Central Limit Theorem to find probabilities concerning the sample mean.
To be able to apply the methods learned in this lesson to new problems.

27.1 - The Theorem

Central Limit Theorem

We don't have the tools yet to prove the Central Limit Theorem, so we'll just go ahead and state it without proof.

Let $X_{1}, X_{2}, \dots, X_{n}$ be a random sample from a distribution (any distribution!) with (finite) mean $μ$ and (finite) variance $σ^{2}$ . If the sample size $n$ is "sufficiently large," then:

the sample mean $\bar{X}$ follows an approximate normal distribution
with mean $E (\bar{X}) = μ_{\bar{X}} = μ$
and variance $V a r (\bar{X}) = σ_{\bar{X}}^{2} = \frac{σ^{2}}{n}$

We write:

$\bar{X} \overset{d}{⟶} N (μ, \frac{σ^{2}}{n})$ as $n \to \infty$

or:

$Z = \frac{\bar{X} - μ}{σ / \sqrt{n}} = \frac{\sum_{i = 1}^{n} X_{i} - n μ}{\sqrt{n} σ} \overset{d}{⟶} N (0, 1)$ as $n \to \infty$ .

So, in a nutshell, the Central Limit Theorem (CLT) tells us that the sampling distribution of the sample mean is, at least approximately, normally distributed, regardless of the distribution of the underlying random sample. In fact, the CLT applies regardless of whether the distribution of the $X_{i}$ is discrete (for example, Poisson or binomial) or continuous (for example, exponential or chi-square). Our focus in this lesson will be on continuous random variables. In the next lesson, we'll apply the CLT to discrete random variables, such as the binomial and Poisson random variables.

You might be wondering why "sufficiently large" appears in quotes in the theorem. Well, that's because the necessary sample size $n$ depends on the skewness of the distribution from which the random sample $X_{i}$ comes:

If the distribution of the $X_{i}$ is symmetric, unimodal or continuous, then a sample size $n$ as small as 4 or 5 yields an adequate approximation.
If the distribution of the $X_{i}$ is skewed, then a sample size $n$ of at least 25 or 30 yields an adequate approximation.
If the distribution of the $X_{i}$ is extremely skewed, then you may need an even larger $n$ .

We'll spend the rest of the lesson trying to get an intuitive feel for the theorem, as well as applying the theorem so that we can calculate probabilities concerning the sample mean.

27.2 - Implications in Practice

As stated on the previous page, we don't yet have the tools to prove the Central Limit Theorem. And, we won't actually get to proving it until late in Stat 415. It would be good though to get an intuitive feel now for how the CLT works in practice. On this page, we'll explore two examples to get a feel for how: ^[11]

the skewness (or symmetry!) of the underlying distribution of $X_{i}$ , and
the sample size $n$

affect how well the normal distribution approximates the actual ("exact") distribution of the sample mean $\bar{X}$ . Well, that's not quite true. We won't actually find the exact distribution of the sample mean in the two examples. We'll instead use simulation to do the work for us. In the first example, we'll take a look at sample means drawn from a symmetric distribution, specifically, the Uniform(0,1) distribution. In the second example, we'll take a look at sample means drawn from a highly skewed distribution, specifically, the chi-square(3) distribution. In each case, we'll see how large the sample size $n$ has to get before the normal distribution does a decent job of approximating the simulated distribution.

Example 27-1

Consider taking random samples of various sizes $n$ from the (symmetric) Uniform (0, 1) distribution. At what sample size $n$ does the normal distribution make a good approximation to the actual distribution of the sample mean?

Solution

Our previous work on the continuous Uniform(0, 1) random variable tells us that the mean of a $U (0, 1)$ random variable is:

$μ = E (X_{i}) = \frac{0 + 1}{2} = \frac{1}{2}$

while the variance of a $U (0, 1)$ random variable is:

$σ^{2} = V a r (X_{i}) = \frac{(1 - 0)^{2}}{12} = \frac{1}{12}$

The Central Limit Theorem, therefore, tells us that the sample mean $\bar{X}$ is approximately normally distributed with mean:

$μ_{\bar{X}} = μ = \frac{1}{2}$

and variance:

$σ_{\bar{X}}^{2} = \frac{σ^{2}}{n} = \frac{1 / 12}{n} = \frac{1}{12 n}$

Now, our end goal is to compare the normal distribution, as defined by the CLT, to the actual distribution of the sample mean. Now, we could do a lot of theoretical work to find the exact distribution of $\bar{X}$ for various sample sizes $n$ . Instead, we'll use simulation to give us a ballpark idea of the shape of the distribution of $\bar{X}$ . Here's an outline of the general strategy that we'll follow:

Specify the sample size $n$ .
Randomly generate 1000 samples of size $n$ from the Uniform (0,1) distribution.
Use the 1000 generated samples to calculate 1000 sample means from the Uniform (0,1) distribution.
Create a histogram of the 1000 sample means.
Compare the histogram to the normal distribution, as defined by the Central Limit Theorem, in order to see how well the Central Limit Theorem works for the given sample size $n$ .

Let's start with a sample size of $n = 1$ . That is, randomly sample 1000 numbers from a Uniform (0,1) distribution, and create a histogram of the 1000 generated numbers. Of course, the histogram should look roughly flat like a Uniform(0,1) distribution. If you're willing to ignore the artifacts of sampling, you can see that our histogram is roughly flat:

Okay, now let's tackle the more interesting sample sizes. Let $n = 2$ . Generating 1000 samples of size $n = 2$ , calculating the 1000 sample means, and creating a histogram of the 1000 sample means, we get:

It can actually be shown that the exact distribution of the sample mean of 2 numbers drawn from the Uniform(0, 1) distribution is the triangular distribution. The histogram does look a bit triangular, doesn't it? The blue curve overlaid on the histogram is the normal distribution, as defined by the Central Limit Theorem. That is, the blue curve is the normal distribution with mean:

$μ_{\bar{X}} = μ = \frac{1}{2}$

and variance:

$σ_{\bar{X}}^{2} = \frac{1}{12 n} = \frac{1}{12 (2)} = \frac{1}{24}$

As you can see, already at $n = 2$ , the normal curve wouldn't do too bad of a job of approximating the exact probabilities. Let's increase the sample size to $n = 4$ . Generating 1000 samples of size $n = 4$ , calculating the 1000 sample means, and creating a histogram of the 1000 sample means, we get:

The blue curve overlaid on the histogram is the normal distribution, as defined by the Central Limit Theorem. That is, the blue curve is the normal distribution with mean:

$μ_{\bar{X}} = μ = \frac{1}{2}$

and variance:

$σ_{\bar{X}}^{2} = \frac{1}{12 n} = \frac{1}{12 (4)} = \frac{1}{48}$

Again, at $n = 4$ , the normal curve does a very good job of approximating the exact probabilities. In fact, it does such a good job, that we could probably stop this exercise already. But let's increase the sample size to $n = 9$ . Generating 1000 samples of size $n = 9$ , calculating the 1000 sample means, and creating a histogram of the 1000 sample means, we get:

The blue curve overlaid on the histogram is the normal distribution, as defined by the Central Limit Theorem. That is, the blue curve is the normal distribution with mean:

$μ_{\bar{X}} = μ = \frac{1}{2}$

and variance:

$σ_{\bar{X}}^{2} = \frac{1}{12 n} = \frac{1}{12 (9)} = \frac{1}{108}$

And not surprisingly, at $n = 9$ , the normal curve does a very good job of approximating the exact probabilities. There is another interesting thing worth noting though, too. As you can see, as the sample size increases, the variance of the sample mean decreases. That's a good thing, as it doesn't seem that it should be any other way. If you think about it, if it were possible to increase the sample size $n$ to something close to the size of the population, you would expect that the resulting sample means would not vary much, and would be close to the population mean. Of course, the trade-off here is that large sample sizes typically cost lots more money than small sample sizes.

Well, just for the heck of it, let's increase our sample size one more time to $n = 16$ . Generating 1000 samples of size $n = 16$ , calculating the 1000 sample means, and creating a histogram of the 1000 sample means, we get:

The blue curve overlaid on the histogram is the normal distribution with mean:

$μ_{\bar{X}} = μ = \frac{1}{2}$

and variance:

$σ_{\bar{X}}^{2} = \frac{1}{12 n} = \frac{1}{12 (16)} = \frac{1}{192}$

Again, at $n = 16$ , the normal curve does a very good job of approximating the exact probabilities. Okay, uncle! That's enough of this example! Let's summarize the two take-away messages from this example:

If the underlying distribution is symmetric, then you don't need a very large sample size for the normal distribution, as defined by the Central Limit Theorem, to do a decent job of approximating the probability distribution of the sample mean.
The larger the sample size $n$ , the smaller the variance of the sample mean.

Example 27-2

Now consider taking random samples of various sizes $n$ from the (skewed) chi-square distribution with 3 degrees of freedom. At what sample size $n$ does the normal distribution make a good approximation to the actual distribution of the sample mean?

Solution

We are going to do exactly what we did in the previous example. The only difference is that our underlying distribution here, that is, the chi-square(3) distribution, is highly-skewed. Now, our previous work on the chi-square distribution tells us that the mean of a chi-square random variable with three degrees of freedom is:

$μ = E (X_{i}) = r = 3$

while the variance of a chi-square random variable with three degrees of freedom is:

$σ^{2} = V a r (X_{i}) = 2 r = 2 (3) = 6$

The Central Limit Theorem, therefore, tells us that the sample mean $\bar{X}$ is approximately normally distributed with mean:

$μ_{\bar{X}} = μ = 3$

and variance:

$σ_{\bar{X}}^{2} = \frac{σ^{2}}{n} = \frac{6}{n}$

Again, we'll follow a strategy similar to that in the above example, namely:

Specify the sample size $n$ .
Randomly generate 1000 samples of size $n$ from the chi-square(3) distribution.
Use the 1000 generated samples to calculate 1000 sample means from the chi-square(3) distribution.
Create a histogram of the 1000 sample means.
Compare the histogram to the normal distribution, as defined by the Central Limit Theorem, in order to see how well the Central Limit Theorem works for the given sample size $n$ .

Again, starting with a sample size of $n = 1$ , we randomly sample 1000 numbers from a chi-square(3) distribution, and create a histogram of the 1000 generated numbers. Of course, the histogram should look like a (skewed) chi-square(3) distribution, as the blue curve suggests it does:

Now, let's consider samples of size $n = 2$ . Generating 1000 samples of size $n = 2$ , calculating the 1000 sample means, and creating a histogram of the 1000 sample means, we get:

The blue curve overlaid on the histogram is the normal distribution, as defined by the Central Limit Theorem. That is, the blue curve is the normal distribution with mean:

$μ_{\bar{X}} = μ = 3$

and variance:

$σ_{\bar{X}}^{2} = \frac{σ^{2}}{n} = \frac{6}{2} = 3$

As you can see, at $n = 2$ , the normal curve wouldn't do a very job of approximating the exact probabilities. The probability distribution of the sample mean still appears to be quite skewed. Let's increase the sample size to $n = 4$ . Generating 1000 samples of size $n = 4$ , calculating the 1000 sample means, and creating a histogram of the 1000 sample means, we get:

The blue curve overlaid on the histogram is the normal distribution, as defined by the Central Limit Theorem. That is, the blue curve is the normal distribution with mean:

$μ_{\bar{X}} = μ = 3$

and variance:

$σ_{\bar{X}}^{2} = \frac{σ^{2}}{n} = \frac{6}{4} = 1.5$

Although, at $n = 4$ , the normal curve is doing a better job of approximating the probability distribution of the sample mean, there is still much room for improvement. Let's try $n = 9$ . Generating 1000 samples of size $n = 9$ , calculating the 1000 sample means, and creating a histogram of the 1000 sample means, we get:

The blue curve overlaid on the histogram is the normal distribution, as defined by the Central Limit Theorem. That is, the blue curve is the normal distribution with mean:

$μ_{\bar{X}} = μ = 3$

and variance:

$σ_{\bar{X}}^{2} = \frac{σ^{2}}{n} = \frac{6}{9} = 0.667$

We're getting closer, but let's really jump up the sample size to, say, $n = 25$ . Generating 1000 samples of size $n = 25$ , calculating the 1000 sample means, and creating a histogram of the 1000 sample means, we get:

The blue curve overlaid on the histogram is the normal distribution, as defined by the Central Limit Theorem. That is, the blue curve is the normal distribution with mean:

$μ_{\bar{X}} = μ = 3$

and variance:

$σ_{\bar{X}}^{2} = \frac{σ^{2}}{n} = \frac{6}{25} = 0.24$

Okay, now we're talking! There's still just a teeny tiny bit of skewness in the sampling distribution. Let's increase the sample size just one more time to, say, $n = 36$ . Generating 1000 samples of size $n = 36$ , calculating the 1000 sample means, and creating a histogram of the 1000 sample means, we get:

The blue curve overlaid on the histogram is the normal distribution, as defined by the Central Limit Theorem. That is, the blue curve is the normal distribution with mean:

$μ_{\bar{X}} = μ = 3$

and variance:

$σ_{\bar{X}}^{2} = \frac{σ^{2}}{n} = \frac{6}{36} = 0.167$

Okay, now, I'm perfectly happy! It appears that, at $n = 36$ , the normal curve does a very good job of approximating the exact probabilities. Let's summarize the two take-away messages from this example:

Again, the larger the sample size $n$ , the smaller the variance of the sample mean. Nothing new there.
If the underlying distribution is skewed, then you need a larger sample size, typically $n > 30$ , for the normal distribution, as defined by the Central Limit Theorem, to do a decent job of approximating the probability distribution of the sample mean.

27.3 - Applications in Practice

Now that we have an intuitive feel for the Central Limit Theorem, let's use it in two different examples. In the first example, we use the Central Limit Theorem to describe how the sample mean behaves, and then use that behavior to calculate a probability. In the second example, we take a look at the most common use of the CLT, namely to use the theorem to test a claim.

Example 27-3

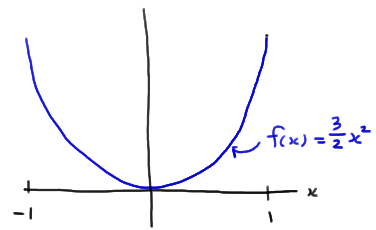
three over two all times x squared graph

Take a random sample of size $n = 15$ from a distribution whose probability density function is:

$f (x) = \frac{3}{2} x^{2}$

for $- 1 < x < 1$ . What is the probability that the sample mean falls between $- \frac{2}{5}$ and $\frac{1}{5}$ ?

Solution

The expected value of the random variable $X$ is 0, as the following calculation illustrates:

$μ = E (X) = \int_{- 1}^{1} x \cdot \frac{3}{2} x^{2} d x = \frac{3}{2} \int_{- 1}^{1} x^{3} d x = \frac{3}{2} {[\frac{x^{4}}{4}]}_{x = - 1}^{x = 1} = \frac{3}{2} (\frac{1}{4} - \frac{1}{4}) = 0$

The variance of the random variable $X$ is $\frac{3}{5}$ , as the following calculation illustrates:

$σ^{2} = E (X - μ)^{2} = \int_{- 1}^{1} (x - 0)^{2} \frac{3}{2} x^{2} d x = \frac{3}{2} \int_{- 1}^{1} x^{4} d x = \frac{3}{2} {[\frac{x^{5}}{5}]}_{x = - 1}^{x = 1} = \frac{3}{2} (\frac{1}{5} + \frac{1}{5}) = \frac{3}{5}$

Therefore, the CLT tells us that the sample mean $\bar{X}$ is approximately normal with mean:

$E (\bar{X}) = μ_{\bar{X}} = μ = 0$

and variance:

$V a r (\bar{X}) = σ_{\bar{X}}^{2} = \frac{σ^{2}}{n} = \frac{3 / 5}{15} = \frac{3}{75} = \frac{1}{25}$

Therefore the standard deviation of $\bar{X}$ is $\frac{1}{5}$ . Drawing a picture of the desired probability:

we see that:

$P (- 2 / 5 < \bar{X} < 1 / 5) = P (- 2 < Z < 1)$

Therefore, using the standard normal table, we get:

$P (- 2 / 5 < \bar{X} < 1 / 5) = P (Z < 1) - P (Z < - 2) = 0.8413 - 0.0228 = 0.8185$

That is, there is an 81.85% chance that a random sample of size 15 from the given distribution will yield a sample mean between $- \frac{2}{5}$ and $\frac{1}{5}$ .

Example 27-4

Let $X_{i}$ denote the waiting time (in minutes) for the $i^{t h}$ customer. An assistant manager claims that $μ$ , the average waiting time of the entire population of customers, is 2 minutes. The manager doesn't believe his assistant's claim, so he observes a random sample of 36 customers. The average waiting time for the 36 customers is 3.2 minutes. Should the manager reject his assistant's claim (... and fire him)?

Solution

It is reasonable to assume that $X_{i}$ is an exponential random variable. And, based on the assistant manager's claim, the mean of $X_{i}$ is:

$μ = θ = 2$ .

Therefore, knowing what we know about exponential random variables, the variance of $X_{i}$ is:

$σ^{2} = θ^{2} = 2^{2} = 4$ .

Now, we need to know, if the mean $μ$ really is 2, as the assistant manager claims, what is the probability that the manager would obtain a sample mean as large as (or larger than) 3.2 minutes? Well, the Central Limit Theorem tells us that the sample mean $\bar{X}$ is approximately normally distributed with mean:

$μ_{\bar{X}} = 2$

and variance:

$σ_{\bar{X}}^{2} = \frac{σ^{2}}{n} = \frac{4}{36} = \frac{1}{9}$

Here's a picture, then, of the normal probability that we need to determine:

$z = \frac{3.2 - 2}{\sqrt{\frac{1}{9}}} = 3.6$

That is:

$P (\bar{X} > 3.2) = P (Z > 3.6)$

The $Z$ value in this case is so extreme that the table in the back of our text book can't help us find the desired probability. But, using statistical software, such as Minitab, we can determine that:

$P (\bar{X} > 3.2) = P (Z > 3.6) = 0.00016$

That is, if the population mean $μ$ really is 2, then there is only a 16/100,000 chance (0.016%) of getting such a large sample mean. It would be quite reasonable, therefore, for the manager to reject his assistant's claim that the mean $μ$ is 2. The manager should feel comfortable concluding that the population mean $μ$ really is greater than 2. We will leave it up to him to decide whether or not he should fire his assistant!

By the way, this is the kind of example that we'll see when we study hypothesis testing in Stat 415. In general, in the process of performing a hypothesis test, someone makes a claim (the assistant, in this case), and someone collects and uses the data (the manager, in this case) to make a decision about the validity of the claim. It just so happens to be that we used the CLT in this example to help us make a decision about the assistant's claim. ^[12]

Lesson 28: Approximations for Discrete Distributions

Overview

In the previous lesson, we explored the Central Limit Theorem, which states that if $X_{1}, X_{2}, \dots, X_{n}$ is a random sample of "sufficient" size n from a population whose mean is $μ$ and standard deviation is $σ$ , then:

$Z = \frac{\bar{X} - μ}{σ / \sqrt{n}} = \frac{\sum_{i = 1}^{n} X_{i} - n μ}{\sqrt{n} σ} \overset{d}{⟶} N (0, 1)$

In that lesson, all of the examples concerned continuous random variables. In this lesson, our focus will be on applying the Central Limit Theorem to discrete random variables. In particular, we will investigate how to use the normal distribution to approximate binomial probabilities and Poisson probabilities.

Objectives

Upon completion of this lesson, you should be able to:

To learn how to use the normal distribution to approximate binomial probabilities.
To learn how to use the normal distribution to approximate Poisson probabilities.
To be able to apply the methods learned in this lesson to new problems.

28.1 - Normal Approximation to Binomial

As the title of this page suggests, we will now focus on using the normal distribution to approximate binomial probabilities. The Central Limit Theorem is the tool that allows us to do so. As usual, we'll use an example to motivate the material.

Example 28-1

Let $X_{i}$ denote whether or not a randomly selected individual approves of the job the President is doing. More specifically:

Let $X_{i} = 1$ , if the person approves of the job the President is doing, with probability $p$
Let $X_{i} = 0$ , if the person does not approve of the job the President is doing with probability $1 - p$

Then, recall that $X_{i}$ is a Bernoulli random variable with mean:

$μ = E (X) = (0) (1 - p) + (1) (p) = p$

and variance:

$σ^{2} = V a r (X) = E [(X - p)^{2}] = (0 - p)^{2} (1 - p) + (1 - p)^{2} (p) = p (1 - p) [p + 1 - p] = p (1 - p)$

Now, take a random sample of $n$ people, and let:

$Y = X_{1} + X_{2} + \dots + X_{n}$

Then $Y$ is a binomial( $n, p$ ) random variable, $y = 0, 1, 2, \dots, n$ , with mean:

$μ = n p$

and variance:

$σ^{2} = n p (1 - p)$

Now, let $n = 10$ and $p = \frac{1}{2}$ , so that $Y$ is binomial( $10, \frac{1}{2}$ ). What is the probability that exactly five people approve of the job the President is doing?

Solution

There is really nothing new here. We can calculate the exact probability using the binomial table in the back of the book with $n = 10$ and $p = \frac{1}{2}$ . Doing so, we get:

$\begin{aligned} P (Y = 5) & = P (Y \leq 5) - P (Y \leq 4) \\ = 0.6230 - 0.3770 \\ = 0.2460 \end{aligned}$

That is, there is a 24.6% chance that exactly five of the ten people selected approve of the job the President is doing.

Note, however, that $Y$ in the above example is defined as a sum of independent, identically distributed random variables. Therefore, as long as $n$ is sufficiently large, we can use the Central Limit Theorem to calculate probabilities for $Y$ . Specifically, the Central Limit Theorem tells us that:

$Z = \frac{Y - n p}{\sqrt{n p (1 - p)}} \overset{d}{⟶} N (0, 1)$ .

Let's use the normal distribution then to approximate some probabilities for $Y$ . Again, what is the probability that exactly five people approve of the job the President is doing?

Solution

First, recognize in our case that the mean is:

$μ = n p = 10 (\frac{1}{2}) = 5$

and the variance is:

$σ^{2} = n p (1 - p) = 10 (\frac{1}{2}) (\frac{1}{2}) = 2.5$

Now, if we look at a graph of the binomial distribution with the rectangle corresponding to $Y = 5$ shaded in red:

we should see that we would benefit from making some kind of correction for the fact that we are using a continuous distribution to approximate a discrete distribution. Specifically, it seems that the rectangle $Y = 5$ really includes any $Y$ greater than 4.5 but less than 5.5. That is:

$P (Y = 5) = P (4.5 < Y < 5.5)$

Such an adjustment is called a "continuity correction." Once we've made the continuity correction, the calculation reduces to a normal probability calculation:

https://www.youtube.com/watch/g1CZLI7vqNM ^[13]

Now, recall that we previous used the binomial distribution to determine that the probability that $Y = 5$ is exactly 0.246. Here, we used the normal distribution to determine that the probability that $Y = 5$ is approximately 0.251. That's not too shabby of an approximation, in light of the fact that we are dealing with a relative small sample size of $n = 10$ !

Let's try a few more approximations. What is the probability that more than 7, but at most 9, of the ten people sampled approve of the job the President is doing?

Solution

If we look at a graph of the binomial distribution with the area corresponding to $7 < Y \leq 9$ shaded in red:

we should see that we'll want to make the following continuity correction:

$P (7 < Y \leq 9) = P (7.5 < Y < 9.5)$

Now again, once we've made the continuity correction, the calculation reduces to a normal probability calculation:

https://www.youtube.com/watch/kErQEQ_boPk ^[14]

By the way, you might find it interesting to note that the approximate normal probability is quite close to the exact binomial probability. We showed that the approximate probability is 0.0549, whereas the following calculation shows that the exact probability (using the binomial table with $n = 10$ and $p = \frac{1}{2}$ is 0.0537:

$P (7 < Y \leq 9) = P (Y \leq 9) - P (Y \leq 7) = 0.9990 - 0.9453 = 0.0537$

Let's try one more approximation. What is the probability that at least 2, but less than 4, of the ten people sampled approve of the job the President is doing?

Solution

If we look at a graph of the binomial distribution with the area corresponding to $2 \leq Y < 4$ shaded in red:

we should see that we'll want to make the following continuity correction:

$P (2 \leq Y < 4) = P (1.5 < Y < 3.5)$

Again, once we've made the continuity correction, the calculation reduces to a normal probability calculation:

$\begin{aligned} P (2 \leq Y < 4) = P (1.5 < Y < 3.5) & = P (\frac{1.5 - 5}{\sqrt{2.5}} < Z < \frac{3.5 - 5}{\sqrt{2.5}}) \\ = P (- 2.21 < Z < - 0.95) \\ = P (Z > 0.95) - P (Z > 2.21) \\ = 0.1711 - 0.0136 = 0.1575 \end{aligned}$

By the way, the exact binomial probability is 0.1612, as the following calculation illustrates:

$P (2 \leq Y < 4) = P (Y \leq 3) - P (Y \leq 1) = 0.1719 - 0.0107 = 0.1612$

Just a couple of comments before we close our discussion of the normal approximation to the binomial.

(1) First, we have not yet discussed what "sufficiently large" means in terms of when it is appropriate to use the normal approximation to the binomial. The general rule of thumb is that the sample size $n$ is "sufficiently large" if:

$n p \geq 5$ and $n (1 - p) \geq 5$

For example, in the above example, in which $p = 0.5$ , the two conditions are met if:

$n p = n (0.5) \geq 5$ and $n (1 - p) = n (0.5) \geq 5$

Now, both conditions are true if:

$n \geq 5 (\frac{10}{5}) = 10$

Because our sample size was at least 10 (well, barely!), we now see why our approximations were quite close to the exact probabilities. In general, the farther $p$ is away from 0.5, the larger the sample size $n$ is needed. For example, suppose $p = 0.1$ . Then, the two conditions are met if:

$n p = n (0.1) \geq 5$ and $n (1 - p) = n (0.9) \geq 5$

Now, the first condition is met if:

$n \geq 5 (10) = 50$

And, the second condition is met if:

$n \geq 5 (\frac{10}{9}) = 5.5$

That is, the only way both conditions are met is if $n \geq 50$ . So, in summary, when $p = 0.5$ , a sample size of $n = 10$ is sufficient. But, if $p = 0.1$ , then we need a much larger sample size, namely $n = 50$ .

(2) In truth, if you have the available tools, such as a binomial table or a statistical package, you'll probably want to calculate exact probabilities instead of approximate probabilities. Does that mean all of our discussion here is for naught? No, not at all! In reality, we'll most often use the Central Limit Theorem as applied to the sum of independent Bernoulli random variables to help us draw conclusions about a true population proportion $p$ . If we take the $Z$ random variable that we've been dealing with above, and divide the numerator by $n$ and the denominator by $n$ (and thereby not changing the overall quantity), we get the following result:

$Z = \frac{\sum X_{i} - n p}{\sqrt{n p (1 - p)}} = \frac{\hat{p} - p}{\sqrt{\frac{p (1 - p)}{n}}} \overset{d}{⟶} N (0, 1)$

The quantity:

$\hat{p} = \frac{\sum_{i = 1}^{n} X_{i}}{n}$

that appears in the numerator is the "sample proportion," that is, the proportion in the sample meeting the condition of interest (approving of the President's job, for example). In Stat 415, we'll use the sample proportion in conjunction with the above result to draw conclusions about the unknown population proportion p. You'll definitely be seeing much more of this in Stat 415! ^[15]

28.2 - Normal Approximation to Poisson

Just as the Central Limit Theorem can be applied to the sum of independent Bernoulli random variables, it can be applied to the sum of independent Poisson random variables. Suppose $Y$ denotes the number of events occurring in an interval with mean $λ$ and variance $λ$ . Now, if $X_{1}, X_{2}, \dots, X_{λ}$ are independent Poisson random variables with mean 1, then:

$Y = \sum_{i = 1}^{λ} X_{i}$

is a Poisson random variable with mean $λ$ . (If you're not convinced of that claim, you might want to go back and review the homework for the lesson on The Moment Generating Function Technique, in which we showed that the sum of independent Poisson random variables is a Poisson random variable.) So, now that we've written $Y$ as a sum of independent, identically distributed random variables, we can apply the Central Limit Theorem. Specifically, when $λ$ is sufficiently large:

$Z = \frac{Y - λ}{\sqrt{λ}} \overset{d}{⟶} N (0, 1)$

We'll use this result to approximate Poisson probabilities using the normal distribution.

Example 28-2

The annual number of earthquakes registering at least 2.5 on the Richter Scale and having an epicenter within 40 miles of downtown Memphis follows a Poisson distribution with mean 6.5. What is the probability that at least 9 such earthquakes will strike next year? (Adapted from An Introduction to Mathematical Statistics, by Richard J. Larsen and Morris L. Marx.)

Solution.

We can, of course use the Poisson distribution to calculate the exact probability. Using the Poisson table with $λ = 6.5$ , we get:

$P (Y \geq 9) = 1 - P (Y \leq 8) = 1 - 0.792 = 0.208$

Now, let's use the normal approximation to the Poisson to calculate an approximate probability. First, we have to make a continuity correction. Doing so, we get:

$P (Y \geq 9) = P (Y > 8.5)$

Once we've made the continuity correction, the calculation again reduces to a normal probability calculation:

$\begin{aligned} P (Y \geq 9) = P (Y > 8.5) & = P (Z > \frac{8.5 - 6.5}{\sqrt{6.5}}) \\ = P (Z > 0.78) = 0.218 \end{aligned}$

So, in summary, we used the Poisson distribution to determine the probability that $Y$ is at least 9 is exactly 0.208, and we used the normal distribution to determine the probability that $Y$ is at least 9 is approximately 0.218. Not too shabby of an approximation!

^[1]	Link
↥	Has Tooltip/Popover
	Toggleable Visibility