Lesson 24: Several Independent Random Variables
Lesson 24: Several Independent Random VariablesIntroduction

In the previous lessons, we explored functions of random variables. We'll do the same in this lesson, too, except here we'll add the requirement that the random variables be independent, and in some cases, identically distributed. Suppose, for example, that we were interested in determining the average weight of the thousands of pumpkins grown on a pumpkin farm. Since we couldn't possibly weigh all of the pumpkins on the farm, we'd want to weigh just a small random sample of pumpkins. If we let:
- \(X_1\) denote the weight of the first pumpkin sampled
- \(X_2\) denote the weight of the second pumpkin sampled
- ...
- \(X_n\) denote the weight of the \(n^{th}\) pumpkin sampled
then we could imagine calculating the average weight of the sampled pumpkins as:
\(\bar{X}=\dfrac{X_1+X_2+\cdots+X_n}{n}\)
Now, because the pumpkins were randomly sampled, we wouldn't expect the weight of one pumpkin, say \(X_1\), to affect the weight of another pumpkin, say \(X_2\). Therefore, \(X_1, X_2, \ldots, X_n\) can be assumed to be independent random variables. And, since \(\bar{X}\) , as defined above, is a function of those independent random variables, it too must be a random variable with a certain probability distribution, a certain mean and a certain variance. Our work in this lesson will all be directed towards the end goal of being able to calculate the mean and variance of the random variable \(\bar{X}\). We'll learn a number things along the way, of course, including a formal definition of a random sample, the expectation of a product of independent variables, and the mean and variance of a linear combination of independent random variables.
Objectives
- To get the big picture for the remainder of the course.
- To learn a formal definition of a random sample.
- To learn what i.i.d. means.
- To learn how to find the expectation of a function of \(n\) independent random variables.
- To learn how to find the expectation of a product of functions of \(n\) independent random variables.
- To learn how to find the mean and variance of a linear combination of random variables.
- To learn that the expected value of the sample mean is \(\mu\).
- To learn that the variance of the sample mean is \(\frac{\sigma^2}{n}\).
- To understand all of the proofs presented in the lesson.
- To be able to apply the methods learned in this lesson to new problems.
24.1 - Some Motivation
24.1 - Some MotivationConsider the population of 8 million college students. Suppose we are interested in determining \(\mu\), the unknown mean distance (in miles) from the students' schools to their hometowns. We can't possibly determine the distance for each of the 8 million students in order to calculate the population mean \(\mu\) and the population variance \(\sigma^2\). We could, however, take a random sample of, say, 100 college students, determine:
\(X_i\)= the distance (in miles) from the home of student \(i\) for \(i=1, 2, \ldots, 100\)
and use the resulting data to learn about the population of college students. How could we obtain that random sample though? Would it be okay to stand outside a major classroom building on the Penn State campus, such as the Willard Building, and ask random students how far they are from their hometown? Probably not! The average distance for Penn State students probably differs greatly from that of college students attending a school in a major city, such as, say The University of California in Los Angeles (UCLA). We need to use a method that ensures that the sample is representative of all college students in the population, not just a subset of the students. Any method that ensures that our sample is truly random will suffice. The following definition formalizes what makes a sample truly random.
Definition. The random variables \(X_i\) constitute a random sample of size \(n\) if and only if:
-
the \(X_i\) are independent, and
-
the \(X_i\) are identically distributed, that is, each \(X_i\) comes from the same distribution \(f(x)\) with mean \(\mu\) and variance \(\sigma^2\).
We say that the \(X_i\) are "i.i.d." (The first i. stands for independent, and the i.d. stands for identically distributed.)
Now, once we've obtained our (truly) random sample, we'll probably want to use the resulting data to calculate the sample mean:
\(\bar{X}=\dfrac{\sum_{i=1}^n X_i}{n}=\dfrac{X_1+X_2+\cdots+X_{100}}{100}\)
and sample variance:
\(S^2=\dfrac{\sum_{i=1}^n (X_i-\bar{X})^2}{n-1}=\dfrac{(X_1-\bar{X})^2+\cdots+(X_{100}-\bar{X})^2}{99}\)
In Stat 415, we'll learn that the sample mean \(\bar{X}\) is the "best" estimate of the population mean \(\mu\) and the sample variance \(S^2\) is the "best" estimate of the population variance \(\sigma^2\). (We'll also learn in what sense the estimates are "best.") Now, before we can use the sample mean and sample variance to draw conclusions about the possible values of the unknown population mean \(\mu\) and unknown population variance \(\sigma^2\), we need to know how \(\bar{X}\) and \(S^2\) behave. That is, we need to know:
- the probability distribution of \(\bar{X}\) and \(S^2\)
- the theoretical mean of of \(\bar{X}\) and \(S^2\)
- the theoretical variance of \(\bar{X}\) and \(S^2\)
Now, note that \(\bar{X}\) and \(S^2\) are sums of independent random variables. That's why we are working in a lesson right now called Several Independent Random Variables. In this lesson, we'll learn about the mean and variance of the random variable \(\bar{X}\). Then, in the lesson called Random Functions Associated with Normal Distributions, we'll add the assumption that the \(X_i\) are measurements from a normal distribution with mean \(\mu\) and variance \(\sigma^2\) to see what we can learn about the probability distribution of \(\bar{X}\) and \(S^2\). In the lesson called The Central Limit Theorem, we'll learn that those results still hold even if our measurements aren't from a normal distribution, providing we have a large enough sample. Along the way, we'll pick up a new tool for our toolbox, namely The Moment-Generating Function Technique. And in the final lesson for the Section (and Course!), we'll see another application of the Central Limit Theorem, namely using the normal distribution to approximate discrete distributions, such as the binomial and Poisson distributions. With our motivation presented, and our curiosity now piqued, let's jump right in and get going!
24.2 - Expectations of Functions of Independent Random Variables
24.2 - Expectations of Functions of Independent Random VariablesOne of our primary goals of this lesson is to determine the theoretical mean and variance of the sample mean:
\(\bar{X}=\dfrac{X_1+X_2+\cdots+X_n}{n}\)
Now, assume the \(X_i\) are independent, as they should be if they come from a random sample. Then, finding the theoretical mean of the sample mean involves taking the expectation of a sum of independent random variables:
\(E(\bar{X})=\dfrac{1}{n} E(X_1+X_2+\cdots+X_n)\)
That's why we'll spend some time on this page learning how to take expectations of functions of independent random variables! A simple example illustrates that we already have a number of techniques sitting in our toolbox ready to help us find the expectation of a sum of independent random variables.
Example 24-1

Suppose we toss a penny three times. Let \(X_1\) denote the number of heads that we get in the three tosses. And, suppose we toss a second penny two times. Let \(X_2\) denote the number of heads we get in those two tosses. If we let:
\(Y=X_1+X_2\)
then \(Y\) denotes the number of heads in five tosses. Note that the random variables \(X_1\) and \(X_2\) are independent and therefore \(Y\) is the sum of independent random variables. Furthermore, we know that:
- \(X_1\) is a binomial random variable with \(n=3\) and \(p=\frac{1}{2}\)
- \(X_2\) is a binomial random variable with \(n=2\) and \(p=\frac{1}{2}\)
- \(Y\) is a binomial random variable with \(n=5\) and \(p=\frac{1}{2}\)
What is the mean of \(Y\), the sum of two independent random variables? And, what is the variance of \(Y\)?
Solution
We can calculate the mean and variance of \(Y\) in three different ways.
-
By recognizing that \(Y\) is a binomial random variable with \(n=5\) and \(p=\frac{1}{2}\), we can use what know about the mean and variance of a binomial random variable, namely that the mean of \(Y\) is:
\(E(Y)=np=5(\frac{1}{2})=\frac{5}{2}\)
and the variance of \(Y\) is:
\(Var(Y)=np(1-p)=5(\frac{1}{2})(\frac{1}{2})=\frac{5}{4}\)
Since sums of independent random variables are not always going to be binomial, this approach won't always work, of course. It would be good to have alternative methods in hand!
-
We could use the linear operator property of expectation. Before doing so, it would be helpful to note that the mean of \(X_1\) is:
\(E(X_1)=np=3(\frac{1}{2})=\frac{3}{2}\)
and the mean of \(X_2\) is:
\(E(X_2)=np=2(\frac{1}{2})=1\)
Now, using the property, we get that the mean of \(Y\) is (thankfully) again \(\frac{5}{2}\):
\(E(Y)=E(X_1+X_2)=E(X_1)+E(X_2)=\dfrac{3}{2}+1=\dfrac{5}{2}\)
Recall that the second equality comes from the linear operator property of expectation. Now, using the linear operator property of expectation to find the variance of \(Y\) takes a bit more work. First, we should note that the variance of \(X_1\) is:
\(Var(X_1)=np(1-p)=3(\frac{1}{2})(\frac{1}{2})=\frac{3}{4}\)
and the variance of \(X_2\) is:
\(Var(X_2)=np(1-p)=2(\frac{1}{2})(\frac{1}{2})=\frac{1}{2}\)
Now, we can (thankfully) show again that the variance of \(Y\) is \(\frac{5}{4}\):
Okay, as if two methods aren't enough, we still have one more method we could use.
-
We could use the independence of the two random variables \(X_1\) and \(X_2\), in conjunction with the definition of expected value of \(Y\) as we know it. First, using the binomial formula, note that we can present the probability mass function of \(X_1\) in tabular form as:
\(x_1\) 0 1 2 3 \(f(x_1)\) \(\frac{1}{8}\) \(\frac{3}{8}\) \(\frac{3}{8}\) \(\frac{1}{8}\) And, we can present the probability mass function of \(X_2\) in tabular form as well:
\(x_2\) 0 1 2 \(f(x_2)\) \(\frac{1}{4}\) \(\frac{2}{4}\) \(\frac{1}{4}\) Now, recall that if \(X_1\) and \(X_2\) are independent random variables, then:
\(f(x_1,x_2)=f(x_1)\cdot f(x_2)\)
We can use this result to help determine \(g(y)\), the probability mass function of \(Y\). First note that, since \(Y\) is the sum of \(X_1\) and \(X_2\), the support of \(Y\) is {0, 1, 2, 3, 4 and 5}. Now, by brute force, we get:
\(g(0)=P(Y=0)=P(X_1=0,X_2=0)=f(0,0)=f_{X_1}(0) \cdot f_{X_2}(0)=\dfrac{1}{8} \cdot \dfrac{1}{4}=\dfrac{1}{32}\)
The second equality comes from the fact that the only way that \(Y\) can equal 0 is if \(X_1=0\) and \(X_2=0\), and the fourth equality comes from the independence of \(X_1\)and \(X_2\). We can make a similar calculation to find the probability that \(Y=1\):
\(g(1)=P(X_1=0,X_2=1)+P(X_1=1,X_2=0)=f_{X_1}(0) \cdot f_{X_2}(1)+f_{X_1}(1) \cdot f_{X_2}(0)=\dfrac{1}{8} \cdot \dfrac{2}{4}+\dfrac{3}{8} \cdot \dfrac{1}{4}=\dfrac{5}{32}\)
The first equality comes from the fact that there are two (mutually exclusive) ways that \(Y\) can equal 1, namely if \(X_1=0\) and \(X_2=1\) or if \(X_1=1\) and \(X_2=0\). The second equality comes from the independence of \(X_1\) and \(X_2\). We can make similar calculations to find \(g(2), g(3), g(4)\), and \(g(5)\). Once we've done that, we can present the p.m.f. of \(Y\) in tabular form as:
\(y = x_1 + x_2\) 0 1 2 3 4 5 \(g(y)\) \(\frac{1}{32}\) \(\frac{5}{32}\) \(\frac{10}{32}\) \(\frac{10}{32}\) \(\frac{5}{32}\) \(\frac{1}{32}\) Then, it is a straightforward calculation to use the definition of the expected value of a discrete random variable to determine that (again!) the expected value of \(Y\) is \(\frac{5}{2}\):
\(E(Y)=0(\frac{1}{32})+1(\frac{5}{32})+2(\frac{10}{32})+\cdots+5(\frac{1}{32})=\frac{80}{32}=\frac{5}{2}\)
The variance of \(Y\) can be calculated similarly. (Do you want to calculate it one more time?!)
The following summarizes the method we've used here in calculating the expected value of \(Y\):
\begin{align} E(Y)=E(X_1+X_2) &= \sum\limits_{x_1 \in S_1}\sum\limits_{x_2 \in S_2} (x_1+x_2)f(x_1,x_2)\\ &= \sum\limits_{x_1 \in S_1}\sum\limits_{x_2 \in S_2} (x_1+x_2)f(x_1) f(x_2)\\ &= \sum\limits_{y \in S} yg(y)\\ \end{align}
The first equality comes, of course, from the definition of \(Y\). The second equality comes from the definition of the expectation of a function of discrete random variables. The third equality comes from the independence of the random variables \(X_1\) and \(X_2\). And, the fourth equality comes from the definition of the expected value of \(Y\), as well as the fact that \(g(y)\) can be determined by summing the appropriate joint probabilities of \(X_1\) and \(X_2\).
The following theorem formally states the third method we used in determining the expected value of \(Y\), the function of two independent random variables. We state the theorem without proof. (If you're interested, you can find a proof of it in Hogg, McKean and Craig, 2005.)
Let \(X_1, X_2, \ldots, X_n\) be \(n\) independent random variables that, by their independence, have the joint probability mass function:
\(f_1(x_1)f_2(x_2)\cdots f_n(x_n)\)
Let the random variable \(Y=u(X_1,X_2, \ldots, X_n)\) have the probability mass function \(g(y)\). Then, in the discrete case:
\(E(Y)=\sum\limits_y yg(y)=\sum\limits_{x_1}\sum\limits_{x_2}\cdots\sum\limits_{x_n}u(x_1,x_2,\ldots,x_n) f_1(x_1)f_2(x_2)\cdots f_n(x_n)\)
provided that these summations exist. For continuous random variables, integrals replace the summations.
In the special case that we are looking for the expectation of the product of functions of \(n\) independent random variables, the following theorem will help us out.
\(E[u_1(x_1)u_2(x_2)\cdots u_n(x_n)]=E[u_1(x_1)]E[u_2(x_2)]\cdots E[u_n(x_n)]\)
That is, the expectation of the product is the product of the expectations.
Proof
For the sake of concreteness, let's assume that the random variables are discrete. Then, the definition of expectation gives us:
\(E[u_1(x_1)u_2(x_2)\cdots u_n(x_n)]=\sum\limits_{x_1}\sum\limits_{x_2}\cdots \sum\limits_{x_n} u_1(x_1)u_2(x_2)\cdots u_n(x_n) f_1(x_1)f_2(x_2)\cdots f_n(x_n)\)
Then, since functions that don't depend on the index of the summation signs can get pulled through the summation signs, we have:
\(E[u_1(x_1)u_2(x_2)\cdots u_n(x_n)]=\sum\limits_{x_1}u_1(x_1)f_1(x_1) \sum\limits_{x_2}u_2(x_2)f_2(x_2)\cdots \sum\limits_{x_n}u_n(x_n)f_n(x_n)\)
Then, by the definition, in the discrete case, of the expected value of \(u_i(X_i)\), our expectation reduces to:
\(E[u_1(x_1)u_2(x_2)\cdots u_n(x_n)]=E[u_1(x_1)]E[u_2(x_2)]\cdots E[u_n(x_n)]\)
Our proof is complete. If our random variables are instead continuous, the proof would be similar. We would just need to make the obvious change of replacing the summation signs with integrals.
Let's return to our example in which we toss a penny three times, and let \(X_1\) denote the number of heads that we get in the three tosses. And, again toss a second penny two times, and let \(X_2\) denote the number of heads we get in those two tosses. In our previous work, we learned that:
- \(E(X_1)=\frac{3}{2}\) and \(\text{Var}(X_1)=\frac{3}{4}\)
- \(E(X_2)=1\) and \(\text{Var}(X_2)=\frac{1}{2}\)
What is the expected value of \(X_1^2X_2\)?
Solution
We'll use the fact that the expectation of the product is the product of the expectations:
24.3 - Mean and Variance of Linear Combinations
24.3 - Mean and Variance of Linear CombinationsWe are still working towards finding the theoretical mean and variance of the sample mean:
\(\bar{X}=\dfrac{X_1+X_2+\cdots+X_n}{n}\)
If we re-write the formula for the sample mean just a bit:
\(\bar{X}=\dfrac{1}{n} X_1+\dfrac{1}{n} X_2+\cdots+\dfrac{1}{n} X_n\)
we can see more clearly that the sample mean is a linear combination of the random variables \(X_1, X_2, \ldots, X_n\). That's why the title and subject of this page! That is, here on this page, we'll add a few a more tools to our toolbox, namely determining the mean and variance of a linear combination of random variables \(X_1, X_2, \ldots, X_n\). Before presenting and proving the major theorem on this page, let's revisit again, by way of example, why we would expect the sample mean and sample variance to have a theoretical mean and variance.
Example 24-2
A statistics instructor conducted a survey in her class. The instructor was interested in learning how many siblings, on average, the students at Penn State University have? She took a random sample of \(n=4\) students, and asked each student how many siblings he/she has. The resulting data were: 0, 2, 1, 1. In an attempt to summarize the data she collected, the instructor calculated the sample mean and sample variance, getting:
\(\bar{X}=\dfrac{4}{4}=1\) and \(S^2=\dfrac{(0-1)^2+(2-1)^2+(1-1)^2+(1-1)^2}{3}=\dfrac{2}{3}\)
The instructor realized though, that if she had asked a different sample of \(n=4\) students how many siblings they have, she'd probably get different results. So, she took a different random sample of \(n=4\) students. The resulting data were: 4, 1, 2, 1. Calculating the sample mean and variance once again, she determined:
\(\bar{X}=\dfrac{8}{4}=2\) and \(S^2=\dfrac{(4-2)^2+(1-2)^2+(2-2)^2+(1-2)^2}{3}=\dfrac{6}{3}=2\)
Hmmm, the instructor thought that was quite a different result from the first sample, so she decided to take yet another sample of \(n=4\) students. Doing so, the resulting data were: 5, 3, 2, 2. Calculating the sample mean and variance yet again, she determined:
\(\bar{X}=\dfrac{12}{4}=3\) and \(S^2=\dfrac{(5-3)^2+(3-3)^2+(2-3)^2+(2-3)^2}{3}=\dfrac{6}{3}=2\)
That's enough of this! I think you can probably see where we are going with this example. It is very clear that the values of the sample mean \(\bar{X}\)and the sample variance \(S^2\) depend on the selected random sample. That is, \(\bar{X}\) and \(S^2\) are continuous random variables in their own right. Therefore, they themselves should each have a particular:
- probability distribution (called a "sampling distribution"),
- mean, and
- variance.
We are still in the hunt for all three of these items. The next theorem will help move us closer towards finding the mean and variance of the sample mean \(\bar{X}\).
Suppose \(X_1, X_2, \ldots, X_n\) are \(n\) independent random variables with means \(\mu_1,\mu_2,\cdots,\mu_n\) and variances \(\sigma^2_1,\sigma^2_2,\cdots,\sigma^2_n\).
Then, the mean and variance of the linear combination \(Y=\sum\limits_{i=1}^n a_i X_i\), where \(a_1,a_2, \ldots, a_n\) are real constants are:
\(\mu_Y=\sum\limits_{i=1}^n a_i \mu_i\)
and:
\(\sigma^2_Y=\sum\limits_{i=1}^n a_i^2 \sigma^2_i\)
respectively.
Proof
Let's start with the proof for the mean first:
Now for the proof for the variance. Starting with the definition of the variance of \(Y\), we have:
\(\sigma^2_Y=Var(Y)=E[(Y-\mu_Y)^2]\)
Now, substituting what we know about \(Y\) and the mean of \(Y\) Y, we have:
\(\sigma^2_Y=E\left[\left(\sum\limits_{i=1}^n a_i X_i-\sum\limits_{i=1}^n a_i \mu_i\right)^2\right]\)
Because the summation signs have the same index (\(i=1\) to \(n\)), we can replace the two summation signs with one summation sign:
\(\sigma^2_Y=E\left[\left(\sum\limits_{i=1}^n( a_i X_i-a_i \mu_i)\right)^2\right]\)
And, we can factor out the constants \(a_i\):
\(\sigma^2_Y=E\left[\left(\sum\limits_{i=1}^n a_i (X_i-\mu_i)\right)^2\right]\)
Now, let's rewrite the squared term as the product of two terms. In doing so, use an index of \(i\) on the first summation sign, and an index of \(j\) on the second summation sign:
\(\sigma^2_Y=E\left[\left(\sum\limits_{i=1}^n a_i (X_i-\mu_i)\right) \left(\sum\limits_{j=1}^n a_j (X_j-\mu_j)\right) \right]\)
Now, let's pull the summation signs together:
\(\sigma^2_Y=E\left[\sum\limits_{i=1}^n \sum\limits_{j=1}^n a_i a_j (X_i-\mu_i) (X_j-\mu_j) \right]\)
Then, by the linear operator property of expectation, we can distribute the expectation:
\(\sigma^2_Y=\sum\limits_{i=1}^n \sum\limits_{j=1}^n a_i a_j E\left[(X_i-\mu_i) (X_j-\mu_j) \right]\)
Now, let's rewrite the variance of \(Y\) by evaluating each of the terms from \(i=1\) to \(n\) and \(j=1\) to \(n\). In doing so, recognize that when \(i=j\), the expectation term is the variance of \(X_i\), and when \(i\ne j\), the expectation term is the covariance between \(X_i\) and \(X_j\), which by the assumed independence, is 0:
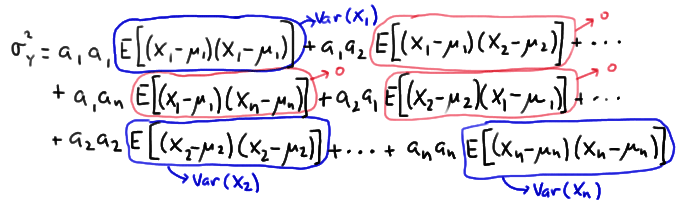
Simplifying then, we get:
\(\sigma^2_Y=a_1^2 E\left[(X_1-\mu_1)^2\right]+a_2^2 E\left[(X_2-\mu_2)^2\right]+\cdots+a_n^2 E\left[(X_n-\mu_n)^2\right]\)
And, simplifying yet more using variance notation:
\(\sigma^2_Y=a_1^2 \sigma^2_1+a_2^2 \sigma^2_2+\cdots+a_n^2 \sigma^2_n\)
Finally, we have:
\(\sigma^2_Y=\sum\limits_{i=1}^n a_i^2 \sigma^2_i\)
as was to be proved.
Example 24-3
Let \(X_1\) and \(X_2\) be independent random variables. Suppose the mean and variance of \(X_1\) are 2 and 4, respectively. Suppose, the mean and variance of \(X_2\) are 3 and 5 respectively. What is the mean and variance of \(X_1+X_2\)?
Solution
The mean of the sum is:
\(E(X_1+X_2)=E(X_1)+E(X_2)=2+3=5\)
and the variance of the sum is:
\(Var(X_1+X_2)=(1)^2Var(X_1)+(1)^2Var(X_2)=4+5=9\)
What is the mean and variance of \(X_1-X_2\)?
Solution
The mean of the difference is:
\(E(X_1-X_2)=E(X_1)-E(X_2)=2-3=-1\)
and the variance of the difference is:
\(Var(X_1-X_2)=Var(X_1+(-1)X_2)=(1)^2Var(X_1)+(-1)^2Var(X_2)=4+5=9\)
That is, the variance of the difference in the two random variables is the same as the variance of the sum of the two random variables.
What is the mean and variance of \(3X_1+4X_2\)?
Solution
The mean of the linear combination is:
\(E(3X_1+4X_2)=3E(X_1)+4E(X_2)=3(2)+4(3)=18\)
and the variance of the linear combination is:
\(Var(3X_1+4X_2)=(3)^2Var(X_1)+(4)^2Var(X_2)=9(4)+16(5)=116\)
24.4 - Mean and Variance of Sample Mean
24.4 - Mean and Variance of Sample MeanWe'll finally accomplish what we set out to do in this lesson, namely to determine the theoretical mean and variance of the continuous random variable \(\bar{X}\). In doing so, we'll discover the major implications of the theorem that we learned on the previous page.
Let \(X_1,X_2,\ldots, X_n\) be a random sample of size \(n\) from a distribution (population) with mean \(\mu\) and variance \(\sigma^2\). What is the mean, that is, the expected value, of the sample mean \(\bar{X}\)?
Solution
Starting with the definition of the sample mean, we have:
\(E(\bar{X})=E\left(\dfrac{X_1+X_2+\cdots+X_n}{n}\right)\)
Then, using the linear operator property of expectation, we get:
\(E(\bar{X})=\dfrac{1}{n} [E(X_1)+E(X_2)+\cdots+E(X_n)]\)
Now, the \(X_i\) are identically distributed, which means they have the same mean \(\mu\). Therefore, replacing \(E(X_i)\) with the alternative notation \(\mu\), we get:
\(E(\bar{X})=\dfrac{1}{n}[\mu+\mu+\cdots+\mu]\)
Now, because there are \(n\) \(\mu\)'s in the above formula, we can rewrite the expected value as:
\(E(\bar{X})=\dfrac{1}{n}[n \mu]=\mu \)
We have shown that the mean (or expected value, if you prefer) of the sample mean \(\bar{X}\) is \(\mu\). That is, we have shown that the mean of \(\bar{X}\) is the same as the mean of the individual \(X_i\).
Let \(X_1,X_2,\ldots, X_n\) be a random sample of size \(n\) from a distribution (population) with mean \(\mu\) and variance \(\sigma^2\). What is the variance of \(\bar{X}\)?
Solution
Starting with the definition of the sample mean, we have:
\(Var(\bar{X})=Var\left(\dfrac{X_1+X_2+\cdots+X_n}{n}\right)\)
Rewriting the term on the right so that it is clear that we have a linear combination of \(X_i\)'s, we get:
\(Var(\bar{X})=Var\left(\dfrac{1}{n}X_1+\dfrac{1}{n}X_2+\cdots+\dfrac{1}{n}X_n\right)\)
Then, applying the theorem on the last page, we get:
\(Var(\bar{X})=\dfrac{1}{n^2}Var(X_1)+\dfrac{1}{n^2}Var(X_2)+\cdots+\dfrac{1}{n^2}Var(X_n)\)
Now, the \(X_i\) are identically distributed, which means they have the same variance \(\sigma^2\). Therefore, replacing \(\text{Var}(X_i)\) with the alternative notation \(\sigma^2\), we get:
\(Var(\bar{X})=\dfrac{1}{n^2}[\sigma^2+\sigma^2+\cdots+\sigma^2]\)
Now, because there are \(n\) \(\sigma^2\)'s in the above formula, we can rewrite the expected value as:
\(Var(\bar{X})=\dfrac{1}{n^2}[n\sigma^2]=\dfrac{\sigma^2}{n}\)
Our result indicates that as the sample size \(n\) increases, the variance of the sample mean decreases. That suggests that on the previous page, if the instructor had taken larger samples of students, she would have seen less variability in the sample means that she was obtaining. This is a good thing, but of course, in general, the costs of research studies no doubt increase as the sample size \(n\) increases. There is always a trade-off!
24.5 - More Examples
24.5 - More ExamplesOn this page, we'll just take a look at a few examples that use the material and methods we learned about in this lesson.
Example 24-4
If \(X_1,X_2,\ldots, X_n\) are a random sample from a population with mean \(\mu\) and variance \(\sigma^2\), then what is:
\(E[(X_i-\mu)(X_j-\mu)]\)
for \(i\ne j\), \(i=1, 2, \ldots, n\)?
Solution
The fact that \(X_1,X_2,\ldots, X_n\) constitute a random sample tells us that (1) \(X_i\) is independent of \(X_j\), for all \(i\ne j\), and (2) the \(X_i\) are identically distributed. Now, we know from our previous work that if \(X_i\) is independent of \(X_j\), for \(i\ne j\), then the covariance between \(X_i\) is independent of \(X_j\) is 0. That is:
\(E[(X_i-\mu)(X_j-\mu)]=Cov(X_i,X_j)=0\)
Example 24-5
Let \(X_1, X_2, X_3\) be a random sample of size \(n=3\) from a distribution with the geometric probability mass function:
\(f(x)=\left(\dfrac{3}{4}\right) \left(\dfrac{1}{4}\right)^{x-1}\)
for \(x=1, 2, 3, \ldots\). What is \(P(\max X_i\le 2)\)?
Solution
The only way that the maximum of the \(X_i\) will be less than or equal to 2 is if all of the \(X_i\) are less than or equal to 2. That is:
\(P(\max X_i\leq 2)=P(X_1\leq 2,X_2\leq 2,X_3\leq 2)\)
Now, because \(X_1,X_2,X_3\) are a random sample, we know that (1) \(X_i\) is independent of \(X_j\), for all \(i\ne j\), and (2) the \(X_i\) are identically distributed. Therefore:
\(P(\max X_i\leq 2)=P(X_1\leq 2)P(X_2\leq 2)P(X_3\leq 2)=[P(X_1\leq 2)]^3\)
The first equality comes from the independence of the \(X_i\), and the second equality comes from the fact that the \(X_i\) are identically distributed. Now, the probability that \(X_1\) is less than or equal to 2 is:
\(P(X\leq 2)=P(X=1)+P(X=2)=\left(\dfrac{3}{4}\right) \left(\dfrac{1}{4}\right)^{1-1}+\left(\dfrac{3}{4}\right) \left(\dfrac{1}{4}\right)^{2-1}=\dfrac{3}{4}+\dfrac{3}{16}=\dfrac{15}{16}\)
Therefore, the probability that the maximum of the \(X_i\) is less than or equal to 2 is:
\(P(\max X_i\leq 2)=[P(X_1\leq 2)]^3=\left(\dfrac{15}{16}\right)^3=0.824\)