Lesson 5: Confidence Intervals for Proportions
Lesson 5: Confidence Intervals for ProportionsOn to yet more population parameters! In this lesson, we derive formulas for \((1-\alpha)100\%\) confidence intervals for:
- a population proportion \(p\)
- the difference in two population proportions, that is, \(p_1-p_2\)
5.1 - One Proportion
5.1 - One ProportionExample 5-1
The article titled "Poll shows increasing concern, little impact with malpractice crisis" in the February 20th, 2003 issue of the Centre Daily Times reported that \(n=418\) Pennsylvanians were surveyed about their opinions about insurance rates. Of the 418 surveyed, \(Y=280\) blamed rising insurance rates on large court settlements against doctors. That is, the sample proportion is:
\(\hat{p}=\dfrac{280}{418}=0.67\)
Use this sample proportion to estimate, with 95% confidence, the parameter \(p\), that is, the proportion of all Pennsylvanians who blame rising insurance rates on large court settlements against doctors.
Answer
We'll need some theory before we can really find the confidence interval for the population proportion \(p\), but we can at least get the ball rolling here. Let:
- \(X_i=1\), if randomly selected Pennsylvanian \(i\) blames rising insurance rates on large court settlements against doctors
- \(X_i=0\), if randomly selected Pennsylvanian \(i\) does not blame rising insurance rates on large court settlements against doctors
Then, the number of Pennsylvanians in the random sample who blame rising insurance rates on large court settlements against doctors is:
\(Y=\sum\limits_{i=1}^{418} X_i=280\)
and therefore, the proportion of Pennsylvanians in the random sample who blame rising insurance rates on large court settlements against doctors is:
\(\hat{p}=\dfrac{\sum_{i=1}^n X_i}{n}=\dfrac{280}{418}=0.67\)
Well, alright, so we're right back where we started, as we basically just repeated what we were given. Well, not quite! That most recent sample proportion was written in order to emphasize the fact that a sample proportion can really be thought of as just a sample average (of 0 and 1 data):
\(\hat{p}=\frac{\sum_{i=1}^n X_i }{n}=0.67\)
Ohhhhh... so that means we can use what we know about the sampling distribution of \(\bar{X}\) to derive a confidence interval for the population proportion \(p\).
Let's jump ahead and state the result, and then we'll step back and prove it.
Theorem
For large random samples, a \((1-\alpha)100\%\) confidence interval for a population proportion \(p\) is:
\(\hat{p}-z_{\alpha/2}\sqrt{\dfrac{\hat{p}(1-\hat{p})}{n}} \leq p \leq \hat{p}+z_{\alpha/2}\sqrt{\dfrac{\hat{p}(1-\hat{p})}{n}}\)
Proof
Okay, so where were we? That's right... we were talking about the the sampling distribution of \(\bar{X}\). Well, we know that the Central Limit Theorem tells us, for large \(n\), that:
\(Z=\dfrac{\bar{X}-\mu}{\sigma/\sqrt{n}}\)
follows, at least approximately, a standard normal distribution \(N(0,1)\). Now, because:
\(Z=\dfrac{\bar{x}-\mu}{\sigma/\sqrt{n}}, \qquad \bar{x}=\hat{p}, \qquad \mu=E(X_i)=p, \qquad \sigma^2=\text{Var}(X_i)=p(1-p) \Rightarrow Z=\frac{\hat{p}-p}{\sqrt{\frac{p(1-p)}{n}}}\)
that implies, for large \(n\), that:
\(Z=\dfrac{\hat{p}-p}{\sqrt{\dfrac{p(1-p)}{n}}}\)
also follows, at least approximately, a standard normal distribution \(N(0,1)\). So, we can do our usual trick of starting with a probability statement:
\(P \left[-z_{\alpha/2}\leq \dfrac{\hat{p}-p}{\sqrt{\dfrac{p(1-p)}{n}}} \leq z_{\alpha/2}\right] \approx 1-\alpha\)
and manipulating the quantity inside the parentheses:
\(-z_{\alpha/2}\leq \dfrac{\hat{p}-p}{\sqrt{\dfrac{p(1-p)}{n}}} \leq z_{\alpha/2} \)
to get the formula for a \((1-\alpha)100\%\) confidence interval for \(p\). Multiplying through the inequality by the quantity in the denominator, we get:
\(-z_{\alpha/2} \sqrt{\dfrac{p(1-p)}{n}} \leq \hat{p}-p \leq z_{\alpha/2} \sqrt{\dfrac{p(1-p)}{n}}\)
Subtracting through the inequality by \(\hat{p}\), we get:
\(-\hat{p}-z_{\alpha/2} \sqrt{\dfrac{p(1-p)}{n}} \leq -p \leq -\hat{p}+z_{\alpha/2}\sqrt{\dfrac{p(1-p)}{n}}\)
And, upon dividing through by −1, and thereby reversing the inequality, we get the claimed \((1-\alpha)100\%\) confidence interval for \(p\):
\(\hat{p}-z_{\alpha/2} \sqrt{\dfrac{p(1-p)}{n}} \leq p \leq \hat{p}+z_{\alpha/2} \sqrt{\dfrac{p(1-p)}{n}}\)
Oooops! What's wrong with that confidence interval? Hmmmm.... it appears that we need to know the population proportion \(p\) in order to estimate the population proportion \(p\).
That's clearly not going to work. What's the logical thing to do? That's right... replace the population proportions (\(p\)) that appear in the endpoints of the interval with sample proportions (\(\hat{p}\)) to get an (approximate) \((1-\alpha)100\%\) confidence interval for \(p\):
\(\hat{p}-z_{\alpha/2} \sqrt{\dfrac{\hat{p}(1-\hat{p})}{n}} \leq p \leq \hat{p}+z_{\alpha/2} \sqrt{\dfrac{\hat{p}(1-\hat{p})}{n}}\)
as was to be proved!
Now that we have that theory behind us, let's return to our example!
Example 5-1 (continued)
The article titled "Poll shows increasing concern, little impact with malpractice crisis" in the February 20th issue of the Centre Daily Times reported that \(n=418\) Pennsylvanians were surveyed about their opinions about insurance rates. Of the 418 surveyed, \(Y=280\) blamed rising insurance rates on large court settlements against doctors. That is, the sample proportion is:
\(\hat{p}=\dfrac{280}{418}=0.67\)
Use this sample proportion to estimate, with 95% confidence, the parameter \(p\), that is, the proportion of all Pennsylvanians who blame rising insurance rates on large court settlements against doctors.
Answer
Plugging \(n=418\), a sample proportion of 0.67, and \(z_{0.025}=1.96\) into the formula for a 95% confidence interval for \(p\), we get:
\(0.67 \pm 1.96\sqrt{\dfrac{0.67(1-0.67)}{418}}\)
which, upon simplifying, is:
\(0.67 \pm 0.045\)
which equals:
\((0.625,0.715)\)
We can be 95% confident that between 62.5% and 71.5% of all Pennsylvanians blame rising insurance rates on large court settlements against doctors.
Minitab®
Using Minitab
As is always the case, you will probably want to calculate your confidence intervals for proportions using statistical software, such as Minitab, rather than doing it by way of formula and calculator. It's easy enough to calculate the (approximate) confidence interval for \(p\) using Minitab:
-
Under the Stat menu, select Basic Statistics, and then 1 Proportion...:
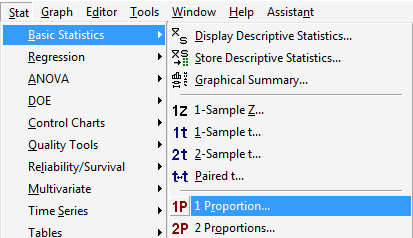
-
In the pop-up window that appears, select Summarized data, and enter the Number of events of interest that occurred, as well as the Number of trials (that is, the sample size n):
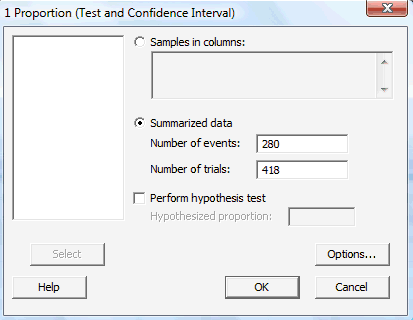
-
Click on the Options... button. If you want a confidence level that differs from the default 95.0 level, specify the desired level in the box labeled Confidence level. Click on the box labeled Use test and interval based on normal distribution. Select OK.
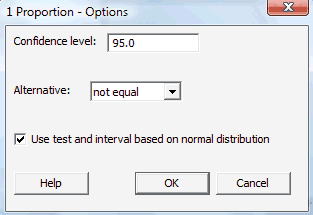
-
Select OK again on the primary pop-up window. The output should appear in the Session window:
Test and CI for One Proportion
| Sample | X | N | Sample p | 95% CI |
|---|---|---|---|---|
| 1 | 280 | 418 | 0.669856 | (0.624775, 0.714938) |
Using the normal approximation.
Notes
- Step 1
Our calculated margin of error is 4.5%:
\(0.67\pm \mathbf{0.045}\)
But, if you go back and take a look at the original article ("Poll shows increasing concern, little impact with malpractice crisis"), the newspaper's reported margin of error is 4.8%. What happened here? Why the difference? One possibility is that the newspaper was taking advantage of what is known about the maximum value of:
\(\hat{p}(1-\hat{p})\)
That is, the maximum value can be shown to be \(\frac{1}{4}\), as demonstrated here:
If we graph the function \(\hat{p}(1-\hat{p})\), it looks (roughly) like this:
We need to find the peak value, that is, the value marked by the red question mark (?). We can do that, of course, by taking the derivative of the function with respect to \(\hat{p}\), setting to 0, and solving for \(\hat{p}\). Taking the derivative and setting to 0, we get:
\(\dfrac{d(\hat{p}-\hat{p}^2)}{d\hat{p}}=1-2\hat{p}\equiv 0\)
And, solving for \(\hat{p}\), we get:
\(\hat{p}=\dfrac{1}{2}\)
Well, that's encouraging... the point at which we've determined that the maximum occurs at least agrees with our graph! Now, what is the value of the function \(\hat{p}(1-\hat{p})\) when \(\hat{p}=\dfrac{1}{2}\)? Well, it is:
\(\hat{p}-\hat{p}^2=\dfrac{1}{2}-\left(\dfrac{1}{2}\right)^2=\dfrac{1}{2}-\dfrac{1}{4}=\dfrac{1}{4}\)
as was claimed.
Because the maximum value of \(\hat{p}(1-\hat{p})\) can be shown to be \(\frac{1}{4}\), the largest the margin of error can be for a 95% confidence interval based on a sample size of \(n=418\) is:
\(1.96\sqrt{\dfrac{\frac{1}{2}(1-\frac{1}{2})}{418}} \approx 2\sqrt{\dfrac{1}{4}} \sqrt{\dfrac{1}{418}}=0.0489\)
Aha! First, that 95% margin of error looks eerily similar to the margin of error claimed by the newspaper. And second, that margin of error makes it look as if we can generalize a bit. Did you notice how we've reduced the 95% margin of error to an (approximate) function of the sample size \(n\)? In general, a 95% margin of error can be approximated by:
\(\dfrac{1}{\sqrt{n}}\)
Here's what that approximate 95% margin of error would like for various sample sizes \(n\):
-
\(n\) 25 64 100 900 1600 95% ME 0.20 0.125 0.10 0.033 0.025
By the way, it is of course entirely possible that the reported margin of error was not determined using the approximate 95% margin of error, as suggested above. It is feasible that the study's authors instead used a higher confidence level, or alternatively calculated the confidence interval using exact methods rather than the normal approximation. - Step 2
The approximate confidence interval for \(p\) that we derived above works well if the following two conditions hold simultaneously:
- \(np=\text{ the number of expected successes }\ge 5\)
- \(n(1-p)=\text{ the number of expected failures }\ge 5\)
5.2 - Two Proportions
5.2 - Two ProportionsExample 5-2
Let's start our exploration of finding a confidence interval for the difference in two proportions by way of an example.
What is the prevalence of anemia in developing countries?
| African Women | Women from Americas | |
| Sample size | 2100 | 1900 |
| Number with anemia | 840 | 323 |
| Sample proportion | \(\dfrac{840}{2100}=0.40\) | \(\dfrac{323}{1900}=0.17\) |
Find a 95% confidence interval for the difference in proportions of all African women with anemia and all women from the Americas with anemia.
Answer
Let's start by simply defining some notation. Let:
- \(n_1\) = the number of African women sampled = 2100
- \(n_2\) = the number of women from the Americas sampled = 1900
- \(y_1\) = the number of African women with anemia = 840
- \(y_2\) = the number of women from the Americas with anemia = 323
Based on these data, we can calculate two sample proportions. The proportion of African women sampled who have anemia is:
\(\hat{p}_1=\dfrac{840}{2100}=0.40\)
And the proportion of women from the Americas sampled who have anemia is:
\(\hat{p}_2=\dfrac{323}{1900}=0.17\)
Now, letting:
- \(p_1\) = the proportion of all African women with anemia
- \(p_2\) = the proportion of all women from the Americas with anemia
we are then interested in finding a 95% confidence interval for \(p_1-p_2\), the difference in the two population proportions. We need to derive a formula for the confidence interval before we can actually calculate it!
Theorem
For large random samples, an (approximate) \((1-\alpha)100\%\) confidence interval for \(p_1-p_2\), the difference in two population proportions, is:
\((\hat{p}_1-\hat{p}_2)\pm z_{\alpha/2} \sqrt{\dfrac{\hat{p}_1(1-\hat{p}_1)}{n_1}+\dfrac{\hat{p}_2(1-\hat{p}_2)}{n_2}}\)
Proof
Let's start with what we know from previous work, namely:
\(\hat{p}_1=\dfrac{Y_1}{n_1} \sim N\left(p_1,\dfrac{p_1(1-p_1)}{n_1}\right)\) and \(\hat{p}_2=\dfrac{Y_2}{n_2} \sim N\left(p_2,\dfrac{p_2(1-p_2)}{n_2}\right)\)
By independence, therefore:
\((\hat{p}_1-\hat{p}_2) \sim N\left(p_1-p_2,\dfrac{p_1(1-p_1)}{n_1}+\dfrac{p_2(1-p_2)}{n_2}\right)\)
Now, it's just a matter of transforming the inside of the typical probability statement:
\(P\left[-z_{\alpha/2} \leq \dfrac{(\hat{p}_1-\hat{p}_2)-(p_1-p_2)}{\sqrt{\dfrac{p_1(1-p_1)}{n_1}+\dfrac{p_2(1-p_2)}{n_2}}} \leq z_{\alpha/2} \right] \approx 1-\alpha\)
That is, we start with this:
\(-z_{\alpha/2} \leq \dfrac{(\hat{p}_1-\hat{p}_2)-(p_1-p_2)}{\sqrt{\dfrac{p_1(1-p_1)}{n_1}+\dfrac{p_2(1-p_2)}{n_2}}} \leq z_{\alpha/2}\)
Multiplying through the inequality by the quantity in the denominator, we get:
\(-z_{\alpha/2}\sqrt{\dfrac{p_1(1-p_1)}{n_1}+\dfrac{p_2(1-p_2)}{n_2}}\leq (\hat{p}_1-\hat{p}_2)-(p_1-p_2) \leq z_{\alpha/2}\sqrt{\dfrac{p_1(1-p_1)}{n_1}+\dfrac{p_2(1-p_2)}{n_2}}\)
Subtracting through the inequality by \(\hat{p}_1-\hat{p}_2\), we get:
\(-(\hat{p}_1-\hat{p}_2)-z_{\alpha/2}\sqrt{\dfrac{p_1(1-p_1)}{n_1}+\dfrac{p_2(1-p_2)}{n_2}}\leq -(p_1-p_2) \leq -(\hat{p}_1-\hat{p}_2)+z_{\alpha/2}\sqrt{\dfrac{p_1(1-p_1)}{n_1}+\dfrac{p_2(1-p_2)}{n_2}}\)
And finally, dividing through the inequality by −1, and rearranging the inequalities, we get our confidence interval:
\((\hat{p}_1-\hat{p}_2)-z_{\alpha/2}\sqrt{\dfrac{p_1(1-p_1)}{n_1}+\dfrac{p_2(1-p_2)}{n_2}}\leq p_1-p_2 \leq (\hat{p}_1-\hat{p}_2)+z_{\alpha/2}\sqrt{\dfrac{p_1(1-p_1)}{n_1}+\dfrac{p_2(1-p_2)}{n_2}}\)
Ooooppps again! What's wrong with the interval? That's right... we need to know the two population proportions in order the estimate the difference in the population proportions!!
That clearly won't work! We can again solve the problem by putting some hats on those population proportions! Doing so, we get the (approximate) \((1-\alpha)100\%\) confidence interval for \(p_1-p_2\):
\((\hat{p}_1-\hat{p}_2)-z_{\alpha/2}\sqrt{\dfrac{\hat{p}_1(1-\hat{p}_1)}{n_1}+\dfrac{\hat{p}_2(1-\hat{p}_2)}{n_2}}\leq p_1-p_2 \leq (\hat{p}_1-\hat{p}_2)+z_{\alpha/2}\sqrt{\dfrac{\hat{p}_1(1-\hat{p}_1)}{n_1}+\dfrac{\hat{p}_2(1-\hat{p}_2)}{n_2}}\)
as claimed.
Example 5-2 (continued)
What is the prevalence of anemia in developing countries?
| African Women | Women from Americas | |
| Sample size | 2100 | 1900 |
| Number with anemia | 840 | 323 |
| Sample proportion | \(\dfrac{840}{2100}=0.40\) | \(\dfrac{323}{1900}=0.17\) |
Find a 95% confidence interval for the difference in proportions of all African women with anemia and all women from the Americas with anemia.
Substituting in the numbers that we know into the formula for a 95% confidence interval for \(p_1-p_2\), we get:
\((0.40-0.17)\pm 1.96 \sqrt{\dfrac{0.40(0.60)}{2100}+\dfrac{0.17(0.83)}{1900}}\)
which simplifies to:
\(0.23\pm 0.027=(0.203, 0.257)\)
We can be 95% confident that there are between 20.3% and 25.7% more African women with anemia than women from the Americas with anemia.
Example 5-3

A social experiment conducted in 1962 involved \(n=123\) three- and four-year-old children from poverty-level families in Ypsilanti, Michigan. The children were randomly assigned either to:
- A treatment group receiving two years of preschool instruction
- A control group receiving no preschool instruction.
The participants were followed into their adult years. Here is a summary of the data:
| Arrested for some crime | ||
| Yes | No | |
| Control | 32 | 30 |
| Preschool | 19 | 42 |
Find a 95% confidence interval for \(p_1-p_2\), the difference in the two population proportions.
Answer
Of the \(n_1=62\) children serving as the control group, 32 were later arrested for some crime, yielding a sample proportion of:
\(\hat{p}_1=0.516\)
And, of the \(n_2=61\) children receiving preschool instruction, 19 were later arrested for some crime, yielding a sample proportion of:
\(\hat{p}_2=0.311\)
A 95% confidence interval for \(p_1-p_2\) is therefore:
\((0.516-0.311)\pm 1.96\sqrt{\dfrac{0.516(0.484)}{62}+\dfrac{0.311(0.689)}{61}}\)
which simplifies to:
\(0.205\pm 0.170=(0.035, 0.375)\)
We can be 95% confident that between 3.5% and 37.5% more children not having attended preschool were arrested for a crime by age 19 than children who had received preschool instruction.
Minitab®
Using Minitab
Yes, Minitab will calculate a confidence interval for the difference in two population proportions for you. To do so:
-
Under the Stat menu, select Basic Statistics, and then select 2 Proportions...:
-
In the pop-up window that appears, select Summarized data, and enter the Number of events, as well as the Number of Trials (that is, the sample sizes \(n_i\)) for each of two groups (First and Second) of interest:
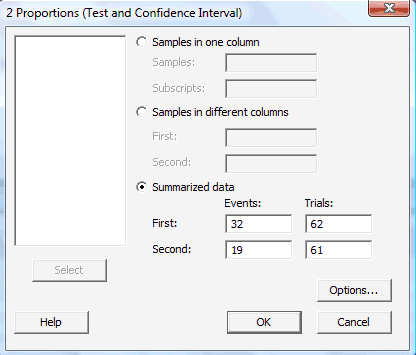
-
Select OK. The output should appear in the Session window:
| Sample | X | N | Sample p |
|---|---|---|---|
| 1 | 32 | 62 | 0.516129 |
| 2 | 19 | 61 | 0.311475 |
Difference = p (1) - p (2)
Estimate for difference: 0.204654
95% CI for difference: (0.0344211, 0.374886)
Test for difference = 0 (vs not =0): Z = 2.36 P-Value = 0.018
Fisher's exact test: P-Value = 0.028