Lesson 16: Chi-Square Goodness-of-Fit Tests
Lesson 16: Chi-Square Goodness-of-Fit TestsSuppose the Penn State student population is 60% female and 40%, male. Then, if a sample of 100 students yields 53 females and 47 males, can we conclude that the sample is (random and) representative of the population? That is, how "good" do the data "fit" the probability model? As the title of the lesson suggests, that's the kind of question that we will answer in this lesson.
16.1 - The General Approach
16.1 - The General ApproachExample 16-1

As is often the case, we'll motivate the methods of this lesson by way of example. Specifically, we'll return to the question posed in the introduction to this lesson.
Suppose the Penn State student population is 60% female and 40%, male. Then, if a sample of 100 students yields 53 females and 47 males, can we conclude that the sample is (random and) representative of the population? That is, how "good" do the data "fit" the assumed probability model of 60% female and 40% male?
Answer
Testing whether there is a "good fit" between the observed data and the assumed probability model amounts to testing:
\(H_0 : p_F =0.60\)
\(H_A : p_F \ne 0.60\)
Now, letting \(Y_1\) denote the number of females selected, we know that \(Y_1\) follows a binomial distribution with n trials and probability of success \(p_1\). That is:
\(Y_1 \sim b(n,p_1)\)
Therefore, the expected value and variance of \(Y_1\) are, respectively:
\(E(Y_1)=np_1\) and \(Var (Y_1) =np_1(1-p_1)\)
And, letting \(Y_2\) denote the number of males selected, we know that \(Y_2 = n − Y_1\) follows a binomial distribution with n trials and probability of success \(p_2\). That is:
\(Y_2 = n-Y_1 \sim (b(n,p_2)=b(n,1-p_1)\)
Therefore, the expected value and variance of \(Y_2\) are, respectively:
\(E(Y_2)=n(1-p_1)=np_2\) and \(Var(Y_2)=n(1-p_1)(1-(1-p_1))=np_1(1-p_1)=np_2(1-p_2)\)
Now, for large samples (\(np_1 ≥ 5\) and \(n(1 − p_1) ≥ 5)\), the Central Limit Theorem yields the normal approximation to the binomial distribution. That is:
\(Z=\dfrac{(Y_1-np_1)}{\sqrt{np_1(1-p_1)}}\)
follows, at least approximately, the standard normal N(0,1) distribution. Therefore, upon squaring Z, we get that:
\(Z^2=Q_1=\dfrac{(Y_1-np_1)^2}{np_1(1-p_1)}\)
follows an approximate chi-square distribution with one degree of freedom. Now, we could stop there. But, that's not typically what is done. Instead, we can rewrite \(Q_1\) a bit. Let's start by multiplying \(Q_1\) by 1 in a special way, that is, by multiplying it by \(\left( \left( 1 − p_1 \right) + p_1 \right)\):
\(Q_1=\dfrac{(Y_1-np_1)^2}{np_1(1-p_1)} \times ((1-p_1)+p_1)\)
Then, distributing the "1" across the numerator, we get:
\(Q_1=\dfrac{(Y_1-np_1)^2(1-p_1)}{np_1(1-p_1)}+\dfrac{(Y_1-np_1)^2p_1}{np_1(1-p_1)}\)
which simplies to:
\(Q_1=\dfrac{(Y_1-np_1)^2}{np_1}+\dfrac{(Y_1-np_1)^2}{n(1-p_1)}\)
Now, taking advantage of the fact that \(Y_1 = n − Y_2\) and \(p_1 = 1 − p_2\), we get:
\(Q_1=\dfrac{(Y_1-np_1)^2}{np_1}+\dfrac{(n-Y_2-n(1-p_2))^2}{np_2}\)
which simplifies to:
\(Q_1=\dfrac{(Y_1-np_1)^2}{np_1}+\dfrac{(-(Y_2-np_2))^2}{np_2}\)
Just one more thing to simplify before we're done:
\(Q_1=\dfrac{(Y_1-np_1)^2}{np_1}+\dfrac{(Y_2-np_2)^2}{np_2}\)
In summary, we have rewritten \(Q_1\) as:
\( Q_1=\sum_{i=1}^{2}\dfrac{(Y_i-np_i)^2}{np_i}=\sum_{i=1}^{2}\dfrac{(\text{OBSERVED }-\text{ EXPECTED})^2}{EXPECTED} \)
We'll use this form of \(Q_1\), and the fact that \(Q_1\) follows an approximate chi-square distribution with one degree of freedom, to conduct the desired hypothesis test.
Before we return to solving the problem posed by our example, a couple of points are worthy of emphasis.
- First, \(Q_1\) has only one degree of freedom, since there is only one independent count, namely \(Y_1\). Once \(Y_1\) is known, the value of \(Y_2 = n − Y_1\) immediately follows.
- Note that the derived approach requires the Central Limit Theorem to kick in. The general rule of thumb is that the expected number of successes must be at least 5 (that is, \(np_1 ≥ 5\)) and the expected number of failures must be at least 5 (that is, \(n(1−p_1) ≥ 5\)).
- The statistic \(Q_1\) will be large if the observed counts are very different from the expected counts. Therefore, we must reject the null hypothesis \(H_0\) if \(Q_1\) is large. How large is large? Large is determined by the values of a chi-square random variable with one degree of freedom, which can be obtained either from a statistical software package, such as Minitab or SAS or from a standard chi-square table, such as the one in the back of our textbook.
- The statistic \(Q_1\) is called the chi-square goodness-of-fit statistic.
Example 16-2

Suppose the Penn State student population is 60% female and 40%, male. Then, if a sample of 100 students yields 53 females and 47 males, can we conclude that the sample is (random and) representative of the population? Use the chi-square goodness-of-fit statistic to test the hypotheses:
\(H_0 : p_F =0.60\)
\(H_A : p_F \ne 0.60\)
using a significance level of \(\alpha = 0.05\).
Answer
The value of the test statistic \(Q_1\) is:
\(Q_1=\dfrac{(53-60)^2}{60}+\dfrac{(47-40)^2}{40}=2.04\)
We should reject the null hypothesis if the observed number of counts is very different from the expected number of counts, that is if \(Q_1\) is large. Because \(Q_1\) follows a chi-square distribution with one degree of freedom, we should reject the null hypothesis, at the 0.05 level, if:
\(Q_1 \ge \chi_{0.05, 1}^{2}=3.84\)
Because:
\(Q_1=2.04 < 3.84\)
we do not reject the null hypothesis. There is not enough evidence at the 0.05 level to conclude that the data don't fit the assumed probability model.
As an aside, it is interesting to note the relationship between using the chi-square goodness of fit statistic \(Q_1\) and the Z-statistic we've previously used for testing a null hypothesis about a proportion. In this case:
\( Z=\dfrac{0.53-0.60}{\sqrt{\frac{(0.60)(0.40)}{100}}}=-1.428 \)
which, you might want to note that, if we square it, we get the same value as we did for \(Q_1\):
\(Q_1=Z^2 =(-1.428)^2=2.04\)
as we should expect. The Z-test for a proportion tells us that we should reject if:
\(|Z| \ge 1.96 \)
Well, again, if we square it, we should see that that's equivalent to rejecting if:
\(Q_1 \ge (1.96)^2 =3.84\)
And not surprisingly, the P-values obtained from the two approaches are identical. The P-value for the chi-square goodness-of-fit test is:
\(P=P(\chi_{(1)}^{2} > 2.04)=0.1532\)
while the P-value for the Z-test is:
\(P=2 \times P(Z>1.428)=2(0.0766)=0.1532\)
Identical, as we should expect!
16.2 - Extension to K Categories
16.2 - Extension to K CategoriesThe work on the previous page is all well and good if your probability model involves just two categories, which as we have seen, reduces to conducting a test for one proportion. What happens if our probability model involves three or more categories? It takes some theoretical work beyond the scope of this course to show it, but the chi-square statistic that we derived on the previous page can be extended to accommodate any number of k categories.
The Extension

Suppose an experiment can result in any of k mutually exclusive and exhaustive outcomes, say \(A_1, A_2, \dots, A_k\). If the experiment is repeated n independent times, and we let \(p_i = P(A_i)\) and \(Y_i\) = the number of times the experiment results in \(A_i, i = 1, \dots, k\), then we can summarize the number of observed outcomes and the number of expected outcomes for each of the k categories in a table as follows:
| Categories | 1 | 2 | . . . | \(k - 1\) | \(k\) |
|---|---|---|---|---|---|
| Observed | \(Y_1\) | \(Y_2\) | . . . | \(Y_{k - 1}\) | \(n - Y_1 - Y_2 - . . . - Y_{k - 1}\) |
| Expected | \(np_1\) | \(np_2\) | . . . | \(np_{k - 1}\) | \(np_k\) |
Karl Pearson showed that the chi-square statistic Q_k−1 defined as:
\[Q_{k-1}=\sum_{i=1}^{k}\frac{(Y_i - np_i)^2}{np_i} \]
follows approximately a chi-square random variable with k−1 degrees of freedom. Let's try it out on an example.
Example 16-3

A particular brand of candy-coated chocolate comes in five different colors that we shall denote as:
- \(A_1 = \text{{brown}}\)
- \(A_2 = \text{{yellow}}\)
- \(A_3 = \text{{orange}}\)
- \(A_4 = \text{{green}}\)
- \(A_5 = \text{{coffee}}\)
Let \(p_i\) equal the probability that the color of a piece of candy selected at random belongs to \(A_i\), for \(i = 1, 2 3, 4, 5\). Test the following null and alternative hypotheses:
\(H_0 : p_{Br}=0.4,p_{Y}=0.2,p_{O}=0.2,p_{G}=0.1,p_{C}=0.1 \)
\(H_A : p_{i} \text{ not specified in null (many possible alternatives) } \)
using a random sample of n = 580 pieces of candy whose colors yielded the respective frequencies 224, 119, 130, 48, and 59. (This example comes from exercises 8.1-2 in the Hogg and Tanis (8th edition) textbook).
Answer
We can summarize the observed \((y_i)\) and expected \((np_i)\) counts in a table as follows:
| Categories | Brown | Yellow | Orange | Green | Coffee | Total |
|---|---|---|---|---|---|---|
| Observed \(y_i\) | 224 | 119 | 130 | 48 | 59 | 580 |
| Assumed \(H_0 (p_i)\) | 0.4 | 0.2 | 0.2 | 0.1 | 0.1 | 1.0 |
| Expected \(np_i\) | 232 | 116 | 116 | 58 | 58 | 580 |
where, for example, the expected number of brown candies is:
\(np_1 = 580(0.40) = 232\)
and the expected number of green candies is:
\(np_4 = 580(0.10) = 58\)
Once we have the observed and expected number of counts, the calculation of the chi-square statistic is straightforward. It is:
\(Q_4=\dfrac{(224-232)^2}{232}+d\frac{(119-116)^2}{116}+\dfrac{(130-116)^2}{116}+\dfrac{(48-58)^2}{58}+\dfrac{(59-58)^2}{58} \)
Simplifying, we get:
\(Q_4=\dfrac{64}{232}+\dfrac{9}{116}+\dfrac{196}{116}+\dfrac{100}{58}+\dfrac{1}{58}=3.784 \)
Because there are k = 5 categories, we have to compare our chi-square statistic \(Q_4\) to a chi-square distribution with k−1 = 5−1 = 4 degrees of freedom:
\(\text{Reject }H_0 \text{ if } Q_4\ge \chi_{4,0.05}^{2}=9.488\)
Because \(Q_4 = 3.784 < 9.488\), we fail to reject the null hypothesis. There is insufficient evidence at the 0.05 level to conclude that the distribution of the color of the candies differs from that specified in the null hypothesis.
By the way, this might be a good time to think about the practical meaning of the term "degrees of freedom." Recalling the example on the last page, we had two categories (male and female) and one degree of freedom. If we are sampling n = 100 people and 53 of them are female, then we absolutely must have 100−53 = 47 males. If we had instead 62 females, then we absolutely must have 100−62 = 38 males. That is, the number of females is the one number that is "free" to be any number, but once it is determined, then the number of males immediately follows. It is in this sense that we have "one degree of freedom."
With the example on this page, we have five categories of candies (brown, yellow, orange, green, coffee) and four degrees of freedom. If we are sampling n = 580 candies, and 224 are brown, 119 are yellow, 130 are orange, and 48 are green, then we absolutely must have 580−(224+119+130+48) = 59 coffee-colored candies. In this case, we have four numbers that are "free" to be any number, but once they are determined, then the number of coffee-colored candies immediately follows. It is in this sense that we have "four degrees of freedom."
16.3 - Unspecified Probabilities
16.3 - Unspecified ProbabilitiesFor the two examples that we've thus far considered, the probabilities were pre-specified. For the first example, we were interested in seeing if the data fit a probability model in which there was a 0.60 probability that a randomly selected Penn State student was female. In the second example, we were interested in seeing if the data fit a probability model in which the probabilities of selecting a brown, yellow, orange, green, and coffee-colored candy was 0.4, 0.2, 0.2, 0.1, and 0.1, respectively. That is, we were interested in testing specific probabilities:
\(H_0 : p_{B}=0.40,p_{Y}=0.20,p_{O}=0.20,p_{G}=0.10,p_{C}=0.10 \)
Someone might be also interested in testing whether a data set follows a specific probability distribution, such as:
\(H_0 : X \sim b(n, 1/2)\)
What if the probabilities aren't pre-specified though? That is, suppose someone is interested in testing whether a random variable is binomial, but with an unspecified probability of success:
\(H_0 : X \sim b(n, p)\)
Can we still use the chi-square goodness-of-fit statistic? The short answer is yes... with just a minor modification.
Example 16-4

Let X denote the number of heads when four dimes are tossed at random. One hundred repetitions of this experiment resulted in 0, 1, 2, 3, and 4 heads being observed on 8, 17, 41, 30, and 4 trials, respectively. Under the assumption that the four dimes are independent, and the probability of getting a head on each coin is p, the random variable X is b(4, p). In light of the observed data, is b(4, p) a reasonable model for the distribution of X?
Answer
In order to use the chi-square statistic to test the data, we need to be able to determine the observed and expected number of trials in which we'd get 0, 1, 2, 3, and 4 heads. The observed part is easy... we know those:
| X | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| Observed | 8 | 17 | 41 | 30 | 4 |
| Expected |
It's the expected numbers that are a problem. If the probability p of getting ahead were specified, we'd be able to calculate the expected numbers. Suppose, for example, that p = 1/2. Then, the probability of getting zero heads in four dimes is:
\(P(X=0)=\binom{4}{0}\left(\dfrac{1}{2}\right)^0\left(\dfrac{1}{2}\right)^4=0.0625 \)
and therefore the expected number of trials resulting in 0 heads is 100 × 0.0625 = 6.25. We could make similar calculations for the case of 1, 2, 3, and 4 heads, and we would be well on our way to using the chi-square statistic:
\(Q_4=\sum_{i=0}^{4}\dfrac{(Obs_i-Exp_i)^2}{Exp_i} \)
and comparing it to a chi-square distribution with 5−1 = 4 degrees of freedom. But, we don't know p, as it is unspecified! What do you think the logical thing would be to do in this case? Sure... we'd probably want to estimate p. But then that begs the question... what should we use as an estimate of p?
One way of estimating p would be to minimize the chi-square statistic \(Q_4\) with respect to p, yielding an estimator \(\tilde{p}\). This \(\tilde{p}\) estimator is called, perhaps not surprisingly, a minimum chi-square estimator of p. If \(\tilde{p}\) is used in calculating the expected numbers that appear in \(Q_4\), it can be shown (not easily, and therefore we won't!) that \(Q_4\) still has an approximate chi-square distribution but with only 4−1 = 3 degrees of freedom. The number of degrees of freedom of the approximating chi-square distribution is reduced by one because we have to estimate one parameter in order to calculate the chi-square statistic. In general, the number of degrees of freedom of the approximating chi-square distribution is reduced by d, the number of parameters estimated. If we estimate two parameters, we reduce the degrees of freedom by two. And so on.
This all seems simple enough. There's just one problem... it is usually very difficult to find minimum chi-square estimators. So what to do? Well, most statisticians just use some other reasonable method of estimating the unspecified parameters, such as maximum likelihood estimation. The good news is that the chi-square statistic testing method still works well. (It should be noted, however, that the approach does provide a slightly larger probability of rejecting the null hypothesis than would the approach based purely on the minimized chi-square.)
Let's summarize
Chi-square method when parameters are unspecified. If you are interested in testing whether a data set fits a probability model with d parameters left unspecified:
- Estimate the d parameters using the maximum likelihood method (or another reasonable method).
- Calculate the chi-square statistic \(Q_{k−1}\) using the obtained estimates.
- Compare the chi-square statistic to a chi-square distribution with (k−1)−d degrees of freedom.
Example 16-5

Let X denote the number of heads when four dimes are tossed at random. One hundred repetitions of this experiment resulted in 0, 1, 2, 3, and 4 heads being observed on 8, 17, 41, 30, and 4 trials, respectively. Under the assumption that the four dimes are independent, and the probability of getting a head on each coin is p, the random variable X is b(4, p). In light of the observed data, is b(4, p) a reasonable model for the distribution of X?
Answer
Given that four dimes are tossed 100 times, we have 400 coin tosses resulting in 205 heads for an estimated probability of success of 0.5125:
\(\hat{p}=\dfrac{0(8)+1(17)+2(41)+3(30)+4(4)}{400}=\dfrac{205}{400}=0.5125 \)
Using 0.5125 as the estimate of p, we can use the binomial p.m.f. (or Minitab!) to calculate the probability that X = 0, 1, ..., 4:
| x | P ( X = x ) |
|---|---|
| 0 | 0.056480 |
| 1 | 0.237508 |
| 2 | 0.374531 |
| 3 | 0.262492 |
| 4 | 0.068988 |
and then, using the probabilities, the expected number of trials resulting in 0, 1, 2, 3, and 4 heads:
| X | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| Observed | 8 | 17 | 41 | 30 | 4 |
| \(P(X = i)\) | 0.0565 | 0.2375 | 0.3745 | 0.2625 | 0.0690 |
| Expected | 5.65 | 23.75 | 37.45 | 26.25 | 6.90 |
Calculating the chi-square statistic, we get:
\(Q_4=\dfrac{(8-5.65)^2}{5.65}+\dfrac{(17-23.75)^2}{23.75}+ ... + \dfrac{(4-6.90)^2}{6.90} =4.99\)
We estimated the d = 1 parameter in calculating the chi-square statistic. Therefore, we compare the statistic to a chi-square distribution with (5−1)−1 = 3 degrees of freedom. Doing so:
\(Q_4= 4.99 < \chi_{3,0.05}^{2}=7.815\)
we fail to reject the null hypothesis. There is insufficient evidence at the 0.05 level to conclude that the data don't fit a binomial probability model.
Let's take a look at another example.
Example 16-6

Let X equal the number of alpha particles emitted from barium-133 in 0.1 seconds and counted by a Geiger counter. One hundred observations of X produced these data.
It is claimed that X follows a Poisson distribution. Use a chi-square goodness-of-fit statistic to test whether this is true.
Answer
Note that very few observations resulted in 0, 1, or 2 alpha particles being emitted in 0.1 second. And, very few observations resulted in 10, 11, or 12 alpha particles being emitted in 0.1 second. Therefore, let's "collapse" the data at the two ends, yielding us nine "not-so-sparse" categories:
| Category | \(X\) | Obs'd |
|---|---|---|
| 1 | 0,1,2* | 5 |
| 2 | 3 | 13 |
| 3 | 4 | 19 |
| 4 | 5 | 16 |
| 5 | 6 | 15 |
| 6 | 7 | 9 |
| 7 | 8 | 12 |
| 8 | 9 | 7 |
| 9 | 10,11,12* | 4 |
| \(n = 100\) |
Because \(\lambda\), the mean of X, is not specified, we can estimate it with its maximum likelihood estimator, namely, the sample mean. Using the data, we get:
\(\bar{x}=\dfrac{1(1)+2(4)+3(13)+ ... + 12(1)}{100}=\dfrac{559}{100}=5.6\)
We can now estimate the probability that an observation will fall into each of the categories. The probability of falling into category 1, for example, is:
\(P(\{1\})=P(X=0)+P(X=1)+P(X=2) =\dfrac{e^{-5.6}5.6^0}{0!}+\dfrac{e^{-5.6}5.6^1}{1!}+\dfrac{e^{-5.6}5.6^2}{2!}=0.0824 \)
Here's what our table looks like now, after adding a column containing the estimated probabilities:
| Category | \(X\) | Obs'd | \(p_i = \left(e^{-5.6}5.6^x\right) / x!\) |
|---|---|---|---|
| 1 | 0,1,2* | 5 | 0.0824 |
| 2 | 3 | 13 | 0.1082 |
| 3 | 4 | 19 | 0.1515 |
| 4 | 5 | 16 | 0.1697 |
| 5 | 6 | 15 | 0.1584 |
| 6 | 7 | 9 | 0.1267 |
| 7 | 8 | 12 | 0.0887 |
| 8 | 9 | 7 | 0.0552 |
| 9 | 10,11,12* | 4 | 0.0539 |
| \(n = 100\) |
Now, we just have to add a column containing the expected number falling into each category. The expected number falling into category 1, for example, is 0.0824 × 100 = 8.24. Doing a similar calculation for each of the categories, we can add our column of expected numbers:
| Category | \(X\) | Obs'd | \(p_i = \left(e^{-5.6}5.6^x\right) / x!\) | Exp'd |
|---|---|---|---|---|
| 1 | 0,1,2* | 5 | 0.0824 | 8.24 |
| 2 | 3 | 13 | 0.1082 | 10.82 |
| 3 | 4 | 19 | 0.1515 | 15.15 |
| 4 | 5 | 16 | 0.1697 | 16.97 |
| 5 | 6 | 15 | 0.1584 | 15.84 |
| 6 | 7 | 9 | 0.1267 | 12.67 |
| 7 | 8 | 12 | 0.0887 | 8.87 |
| 8 | 9 | 7 | 0.0552 | 5.52 |
| 9 | 10,11,12* | 4 | 0.0539 | 5.39 |
| \(n = 100\) | 99.47 |
Now, we can use the observed numbers and the expected numbers to calculate our chi-square test statistic. Doing so, we get:
\(Q_{9-1}=\dfrac{(5-8.24)^2}{8.24}+\dfrac{(13-10.82)^2}{10.82}+ ... +\dfrac{(4-5.39)^2}{5.39}=5.7157 \)
Because we estimated d = 1 parameter, we need to compare our chi-square statistic to a chi-square distribution with (9−1)−1 = 7 degrees of freedom. That is, our critical region is defined as:
\(\text{Reject } H_0 \text{ if } Q_8 \ge \chi_{8-1, 0.05}^{2}=\chi_{7, 0.05}^{2}=14.07 \)
Because our test statistic doesn't fall in the rejection region, that is:
\(Q_8=5.77157 < \chi_{7, 0.05}^{2}=14.07\)
we fail to reject the null hypothesis. There is insufficient evidence at the 0.05 level to conclude that the data don't fit a Poisson probability model.
16.4 - Continuous Random Variables
16.4 - Continuous Random VariablesWhat if we are interested in using a chi-square goodness-of-fit test to see if our data follow some continuous distribution? That is, what if we want to test:
\( H_0 : F(w) =F_0(w)\)
where \(F_0 (w)\) is some known, specified distribution. Clearly, in this situation, it is no longer obvious what constitutes each of the categories. Perhaps we could all agree that the logical thing to do would be to divide up the interval of possible values into k "buckets" or "categories," called \(A_1, A_2, \dots, A_k\), say, into which the observed data can fall. Letting \(Y_i\) denote the number of times the observed value of W belongs to bucket \(A_i, i = 1, 2, \dots, k\), the random variables \(Y_1, Y_2, \dots, Y_k\) follow a multinomial distribution with parameters \(n, p_1, p_2, \dots, p_{k−1}\). The hypothesis that we actually test is a modification of the null hypothesis above, namely:
\(H_{0}^{'} : p_i = p_{i0}, i=1, 2, \dots , k \)
The hypothesis is rejected if the observed value of the chi-square statistic:
\(Q_{k-1} =\sum_{i=1}^{k}\frac{(Obs_i - Exp_i)^2}{Exp_i}\)
is at least as great as \(\chi_{\alpha}^{2}(k-1)\). If the hypothesis \(H_{0}^{'} : p_i = p_{i0}, i=1, 2, \dots , k\) is not rejected, then we do not reject the original hypothesis \(H_0 : F(w) =F_0(w)\) .
Let's make this proposed procedure more concrete by taking a look at an example.
Example 16-7
The IQs of one-hundred randomly selected people were determined using the Stanford-Binet Intelligence Quotient Test. The resulting data were, in sorted order, as follows:
| 54 | 66 | 74 | 74 | 75 | 78 | 79 | 80 | 81 | 82 |
|---|---|---|---|---|---|---|---|---|---|
| 82 | 82 | 83 | 84 | 87 | 88 | 88 | 88 | 88 | 89 |
| 89 | 89 | 89 | 89 | 90 | 90 | 90 | 91 | 92 | 93 |
| 93 | 93 | 94 | 96 | 96 | 97 | 97 | 98 | 98 | 99 |
| 99 | 99 | 99 | 99 | 100 | 100 | 100 | 102 | 102 | 102 |
| 102 | 102 | 103 | 103 | 104 | 104 | 104 | 105 | 105 | 105 |
| 105 | 106 | 106 | 106 | 107 | 107 | 108 | 108 | 108 | 109 |
| 109 | 109 | 110 | 111 | 111 | 111 | 111 | 112 | 112 | 112 |
| 114 | 114 | 115 | 115 | 115 | 116 | 118 | 118 | 120 | 121 |
| 121 | 122 | 123 | 125 | 126 | 127 | 127 | 131 | 132 | 139 |
Test the null hypothesis that the data come from a normal distribution with a mean of 100 and a standard deviation of 16.
Answer
Hmm. So, where do we start? Well, we first have to define some categories. Let's divide up the interval of possible IQs into \(k = 10\) sets of equal probability \(\dfrac{1}{k} = \dfrac{1}{10}\). Perhaps this is best seen pictorially:
So, what's going on in this picture? Well, first the normal density is divided up into 10 intervals of equal probability (0.10). Well, okay, so the picture is not drawn very well to scale. At any rate, we then find the IQs that correspond to the \(k = 10\) cumulative probabilities of 0.1, 0.2, 0.3, etc. This is done in two steps:
- Step 1
first by finding the Z-scores associated with the cumulative probabilities 0.1, 0.2, 0.3, etc.
- Step 2
then by converting each Z-score into an X-value. It is those X-values (IQs) that will make up the "right-hand side" of each bucket:
Category \(X\) Obs'd \(p_i = \left(e^{-5.6}5.6^x\right) / x!\) Exp'd 1 0,1,2* 5 0.0824 8.24 2 3 13 0.1082 10.82 3 4 19 0.1515 15.15 4 5 16 0.1697 16.97 5 6 15 0.1584 15.84 6 7 9 0.1267 12.67 7 8 12 0.0887 8.87 8 9 7 0.0552 5.52 9 10,11,12* 4 0.0539 5.39 \(n = 100\) 99.47 -
Now, it's just a matter of counting the number of observations that fall into each bucket to get the observed (Obs'd) column, and calculating the expected number (0.10 × 100 = 10) to get the expected (Exp'd) column:Category Class 1 (\(-\infty\),79.5) 2 (79.5, 86.5) 3 (86.5, 91.6) 4 (91.6, 95.9) 5 (95.9, 100.0) 6 (100.0, 104.1) 7 (104.1, 108.4) 8 (108.4, 113.5) 9 (113.5, 120.5) 10 (120.5, \(\infty\))
-
| Category | Class | Obs'd | Exp'd | Contribution to \(Q\) |
|---|---|---|---|---|
| 1 | (\(-\infty\),79.5) | 7 | 10 | \(\left(7-10\right)^2 / 10 = 0.9\) |
| 2 | (79.5, 86.5) | 7 | 10 | \(\left(7-10\right)^2 / 10 = 0.9\) |
| 3 | (86.5, 91.6) | 14 | 10 | \(\left(14-10\right)^2 / 10 = 1.6\) |
| 4 | (91.6, 95.9) | 5 | 10 | \(\left(5-10\right)^2 / 10 = 2.5\) |
| 5 | (95.9, 100.0) | 14 | 10 | \(\left(14-10\right)^2 / 10 = 1.6\) |
| 6 | (100.0, 104.1) | 10 | 10 | \(\left(10-10\right)^2 / 10 = 0.0\) |
| 7 | (104.1, 108.4) | 12 | 10 | \(\left(12-10\right)^2 / 10 = 0.4\) |
| 8 | (108.4, 113.5) | 11 | 10 | \(\left(11-10\right)^2 / 10 = 0.1\) |
| 9 | (113.5, 120.5) | 9 | 10 | \(\left(9-10\right)^2 / 10 = 0.1\) |
| 10 | (120.5, \(\infty\)) | 11 | 10 | \(\left(11-10\right)^2 / 10 = 0.1\) |
| \(n = 100\) | \(n = 100\) | \(Q_9 = 8.2\) |
As illustrated in the table, using the observed and expected numbers, we see that the chi-square statistic is 8.2. We reject if the following is true:
\(Q_9 =8.2 \ge \chi_{10-1, 0.05}^{2} =\chi_{9, 0.05}^{2}=16.92\)
It isn't! We do not reject the null hypothesis at the 0.05 level. There is insufficient evidence to conclude that the data do not follow a normal distribution with a mean of 100 and a standard deviation 16.
16.5 - Using Minitab to Lighten the Workload
16.5 - Using Minitab to Lighten the WorkloadExample 16-8
This is how I used Minitab to help with the calculations of the alpha particle example on the Unspecified Probabilities page in this lesson.
-
Use Minitab's Calc >> Probability distribution >> Poisson command to determine the Poisson(5.6) probabilities:
Poisson with mean = 5.6 x P (X = x) 0 0.003698 1 0.020708 2 0.057983 3 0.108234 4 0.151528 5 0.169711 6 0.158397 7 0.126717 8 0.088702 9 0.055193 10 0.030908 11 0.015735 12 0.007343 -
Enter the observed counts into one column and copy the probabilities (collapsing some categories, if necessary) into another column. Use Minitab's Calc >> Calculator command to generate the remaining necessary columns:
Poisson with mean = 5.6 Row Obsd p_i Expd Chisq 1 5 0.082389 8.2389 1.27329 2 15 0.108234 10.8234 0.43772 3 19 0.151528 15.1528 0.97678 4 16 0.169711 16.9711 0.05557 5 15 0.158397 15.8397 0.04451 6 9 0.126717 12.6717 1.06390 7 12 0.088702 8.8702 1.10433 8 7 0.055193 5.5193 0.39724 9 4 0.053986 5.3986 0.36233 Sum up the "Chisq" column to obtain the chi-square statistic Q.
-
-
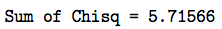
Example 16-9
This is how I used Minitab to help with the calculations of the IQ example on the Continuous Random Variables page in this lesson.
-
The sorted data:
Sample 54 66 74 74 75 78 79 80 81 82 82 82 83 84 87 88 88 88 88 89 89 89 89 89 90 90 90 91 92 93 93 93 94 96 96 97 97 98 98 99 99 99 99 99 100 100 100 102 102 102 102 102 103 103 104 104 104 105 105 105 105 106 106 106 107 107 108 108 108 109 109 109 110 111 111 111 111 112 112 112 114 114 115 115 115 116 118 118 120 121 121 122 123 125 126 127 127 131 132 139 -
The working table:
Row CProb Z Sample Obsd Expd Chisq 1 0.1 -1.28155 79.495 7 10 0.9 2 0.2 -0.84162 86.534 7 10 0.9 3 0.3 -0.52440 91.610 14 10 1.6 4 0.4 -0.25355 95.946 5 10 2.5 5 0.5 0.00000 100.000 14 10 1.6 6 0.6 0.25355 104.054 10 10 0.0 7 0.7 0.52440 108.390 12 10 0.4 8 0.8 0.84162 113.466 11 10 0.1 9 0.9 1.28155 120.505 9 10 0.1 10 11 10 0.1
-
-
The chi-square statistic: