As is generally the case, let's motivate the method for calculating a confidence interval for a population median \(m\) by way of a concrete example. Suppose \(Y_1<Y_2<Y_3<Y_4<Y_5\) are the order statistics of a random sample of size \(n=5\) from a continuous distribution. Our work from the previous lesson tells us that \(Y_3\) serves as a good point estimator of the median \(m\). Let's see what we can come up with for a confidence interval given we have these order statistics at our disposal. Well, suppose we suggested that the interval constrained by the first and fifth order statistics, that is, \((Y_1, Y_5)\) would serve as a good interval. How confident can we be that the interval \(Y_1, Y_5)\) would contain the unknown population median \(m\)? To answer that question, we simply need to calculate the following probability:

\(P(Y_1<m<Y_5)\)

Calculating the probability reduces to a simple binomial calculation once we figure out all the ways in which the population median \(m\) is sandwiched between \(Y_1\) and \(Y_5\). Well, the population median m is sandwiched between \(Y_1\) and \(Y_5\), if the first order statistic is the only order statistic less than the median \(m\):

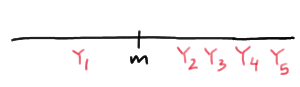
The population median \(m\) is sandwiched between \(Y_1\) and \(Y_5\), if the first two order statistics are the only order statistics less than the median \(m\):

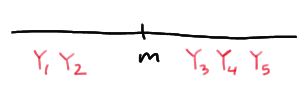
The population median \(m\) is sandwiched between \(Y_1\) and \(Y_5\), if the first three order statistics are less than the median \(m\), and the fourth and fifth order statistics are greater than \(m\):

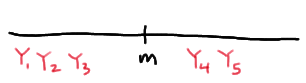
And, the population median \(m\) is sandwiched between \(Y_1\) and \(Y_5\), if the fifth order statistic is the only order statistic greater than the median \(m\):

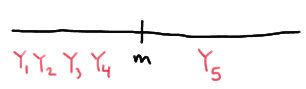
This means that in order to calculate the probability \(P(Y_1<m<Y_5)\), we need to calculate the probability of each of the above events. Now, if we let \(W\) denote the number of \(X_i<m\), then \(W\) is a binomial random variable with \(n\) mutually independent trials and probability of success \(p=P(X_i<m)=0.5\). And, reviewing the events as depicted above, the desired probability is calculated as:

\(P(Y_1<m<Y_5)=P(W=1)+P(W=2)+P(W=3)+P(W=4)\)

The binomial p.m.f. (or, alternatively, the binomial table) makes the calculation straightforward:

\(P(Y_1<m<Y_5)=\sum_{k=1}^{4}P(W=k)=\sum_{k=1}^{4}\binom{5}{k}(0.5)^k(0.5)^{5-k}=0.9376 \)

So, the probability that the random interval \((Y_1, Y_5)\) contains the median \(m\) is 0.9376. We aren't always so lucky with arriving at a decent confidence coefficient on our first try. Sometimes we have to try again aiming to get a confidence coefficient that it as least 90%, but as close to 95% as possible. In this case, the confidence coefficient for the interval \((Y_2, Y_4)\) is:

\(P(Y_2<m<Y_4)=\sum_{k=2}^{3}P(W=k)=\sum_{k=2}^{3}\binom{5}{k}(0.5)^k(0.5)^{5-k}=0.6250 \)

Clearly, we would be better served to stick with the interval \((Y_1, Y_5)\) in this case. Let's take a look at an example.

Yeehaw! The authors of your textbook did a very kind thing for us by calculating the confidence coefficients for confidence intervals for the median \(m\) for various sample sizes \(n\). The resulting confidence coefficients are reported in the following table (or you can look in your text book if you don't want to use a magnifying glass to see this one):

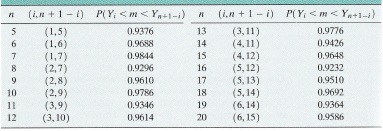
The reading of the table is pretty straightforward. For example, if we have a sample of size \(n=12\), the table tells us we can be 96.14% confident that the population median falls in the interval constrained by the third and tenth order statistic, that is, in the interval \((Y_3, Y_{10})\). And, if we have a sample of size \(n=18\), the table tells us we can be 96.92% confident that the population median falls in the interval constrained by the fifth and fourteenth order statistic, that is, in the interval \((Y_5, Y_{14})\).

All of our confidence coefficient calculations have involved binomial probabilities. It stands to reason, then, that if our sample size \(n\) is larger than 20, say, we could use the normal approximation to the binomial distribution. In our case, \(W\), the number of \(X_i<m\), follows a binomial distribution with mean and variance:

\(\mu=np=0.5n\) and \(\sigma^2=np(1-p)=0.5(1-0.5)n=0.25n\)

respectively. Therefore:

\(Z=\frac{W-0.5n}{\sqrt{0.25n}} \)

follows, at least approximately, the standard normal \(N(0,1)\) distribution.

The method that we learned for finding a confidence interval for the median of a continuous distribution can be easily extended so that we can find a confidence interval for any percentile \(\pi_p\). The only thing we have to change is the probability of a success, that is, that \(X_i\) is less than \(\pi_p\):

\(p=P(X_i < \pi_p)\)

Then, the exact confidence coefficient is calculated just as before using the binomial distribution with parameters \(n\) and \(p\):

\(1-\alpha=P(Y_i < \pi_p < Y_j)=\sum_{k=i}^{j-1}\binom{n}{k}p^k(1-p)^{n-k}\)

And, for large samples of size \(n\ge 20\), say, an approximate confidence coefficient is calculated using the normal approximation to the binomial by way of the standard normal random variable:

\(Z=\dfrac{W-np}{\sqrt{np(1-p)}}\)

Once the sample is observed and the order statistics determined, then the known interval \((y_i, y_j)\) serves as a \(100(1-\alpha)\%\) confidence interval for the unknown population percentile \(\pi_p\). Let's revisit an example from the previous page.