Lesson 22: Kolmogorov-Smirnov Goodness-of-Fit Test
Lesson 22: Kolmogorov-Smirnov Goodness-of-Fit TestOverview

In this lesson, we'll learn how to conduct a test to see how well a hypothesized distribution function \(F(x)\) fits an empirical distribution function \(F_{n}(x)\). The "goodness-of-fit test" that we'll learn about was developed by two probabilists, Andrey Kolmogorov and Vladimir Smirnov, and hence the name of this lesson. In the process of learning about the test, we'll:
- learn a formal definition of an empirical distribution function
- justify, but not derive, the Kolmogorov-Smirnov test statistic
- try out the test on a few examples
- learn how to calculate a confidence band for a distribution function \(F(x)\)
22.1 - The Test
22.1 - The TestBefore we can work on developing a hypothesis test for testing whether an empirical distribution function \(F_n (x)\) fits a hypothesized distribution function \(F (x)\) we better have a good idea of just what is an empirical distribution function \(F_n (x)\). Therefore, let's start with formally defining it.
- Empirical distribution function
-
Given an observed random sample \(X_1 , X_2 , \dots , X_n\), an empirical distribution function \(F_n (x)\) is the fraction of sample observations less than or equal to the value x. More specifically, if \(y_1 < y_2 < \dots < y_n\) are the order statistics of the observed random sample, with no two observations being equal, then the empirical distribution function is defined as:
That is, for the case in which no two observations are equal, the empirical distribution function is a "step" function that jumps \(1/n\) in height at each observation \(x_k\). For the cases in which two (or more) observations are equal, that is, when there are \(n_k\) observations at \(x_k\), the empirical distribution function is a "step" function that jumps \(n_k/n\) in height at each observation \(x_k\). In either case, the empirical distribution function \(F_n(x)\) is the fraction of sample values that are equal to or less than x.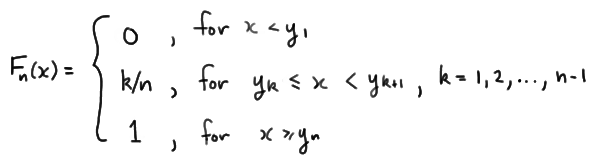
Such a formal definition is all well and good, but it would probably make even more sense if we took at a look at a simple example.
Example 22-1

A random sample of n = 8 people yields the following (ordered) counts of the number of times they swam in the past month:
0 1 2 2 4 6 6 7
Calculate the empirical distribution function \(F_n (x)\).
Answer
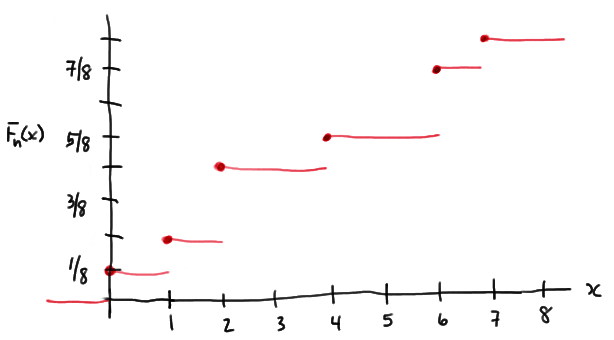
As reported, the data are ordered, therefore the order statistics are \(y_1 = 0, y_2 = 1, y_3 = 2, y_4 = 2, y_5 = 4, y_6 = 6, y_7 = 6\) and \(y_8 = 7\). Therefore, using the definition of the empirical distribution function, we have:
\(F_n(x)=0 \text{ for } x < 0\)
and:
\(F_n(x)=\frac{1}{8} \text{ for } 0 \le x < 1\) and \(F_n(x)=\frac{2}{8} \text{ for } 1 \le x < 2\)
Now, noting that there are two 2s, we need to jump 2/8 at x = 2:
\(F_n(x)=\frac{2}{8}+\frac{2}{8}=\frac{4}{8} \text{ for } 2 \le x < 4\)
Then:
\(F_n(x)=\frac{5}{8} \text{ for } 4 \le x < 6\)
Again, noting that there are two 6s, we need to jump 2/8 at x = 6:
\(F_n(x)=\frac{5}{8}+\frac{2}{8}=\frac{7}{8} \text{ for } 6 \le x < 7\)
And, finally:
\(F_n(x)=\frac{7}{8}+\frac{1}{8}=\frac{8}{8}=1 \text{ for } x \ge 7\)
Plotting the function, it should look something like this then:
Now, with that behind us, let's jump right in and state and justify (not prove!) the Kolmogorov-Smirnov statistic for testing whether an empirical distribution fits a hypothesized distribution well.
- Kolmogorov-Smirnov test statistic
-
\[D_n=sup_x\left[ |F_n(x)-F_0(x)| \right]\]
is used for testing the null hypothesis that the cumulative distribution function \(F (x)\) equals some hypothesized distribution function \(F_0 (x)\), that is, \(H_0 : F(x)=F_0(x)\), against all of the possible alternative hypotheses \(H_A : F(x) \ne F_0(x)\). That is, \(D_n\) is the least upper bound of all pointwise differences \(|F_n(x)-F_0(x)|\).
The bottom line is that the Kolmogorov-Smirnov statistic makes sense, because as the sample size n approaches infinity, the empirical distribution function \(F_n (x)\) converges, with probability 1 and uniformly in x, to the theoretical distribution function \(F (x)\). Therefore, if there is, at any point x, a large difference between the empirical distribution \(F_n (x)\) and the hypothesized distribution \(F_0 (x)\), it would suggest that the empirical distribution \(F_n (x)\) does not equal the hypothesized distribution \(F_0 (x)\). Therefore, we reject the null hypothesis:
\[H_0 : F(x)=F_0(x)\]
if \(D_n\) is too large.
Now, how do we know that \(F_n (x)\) converges, with probability 1 and uniformly in x, to the theoretical distribution function \(F (x)\)? Well, unfortunately, we don't have the tools in this course to officially prove it, but we can at least do a bit of a hand-waving argument.
Let \(X_1 , X_2 , \dots , X_n\) be a random sample of size n from a continuous distribution \(F (x)\). Then, if we consider a fixed x, then \(W= F_n (x)\) can be thought of as a random variable that takes on possible values \(0, 1/n , 2/n , \dots , 1\). Now:
- nW = 1, if and only if exactly 1 observation is less than or equal to x, and n−1 observations are greater than x
- nW = 2, if and only if exactly 2 observations are less than or equal to x, and n−2 observations are greater than x
- and in general...
- nW = k, if and only if exactly k observations are less than or equal to x, and n−k observations are greater than x
If we treat a success as an observation being less than or equal to x, then the probability of success is:
\(P(X_i ≤ x) = F(x)\)
Do you see where this is going? Well, because \(X_1 , X_2 , \dots , X_n\) are independent random variables, the random variable nW is a binomial random variable with n trials and probability of success p = F(x). Therefore:
\[ P\left(W = \frac{k}{n}\right) = P(nW=k) = \binom{n}{k}[F(x)]^k[1-F(x)]^{n-k}\]
And, the expected value and variance of nW are:
\(E(nW)=np=nF(x)\) and \(Var(nW)=np(1-p)=n[F(x)][1-F(x)]\)
respectively. Therefore, the expected value and variance of W are:
\(E(W)=n\frac{F(x)}{n}=F(x)\) and \(\displaystyle Var(W) =\frac{n[(F(x)][1-F(x)]}{n^2}=\frac{[(F(x)][1-F(x)]}{n}\)
We're very close now. We just now need to recognize that as n approaches infinity, the variance of W, that is, the variance of \(F_n (x)\) approaches 0. That means that as n approaches infinity the empirical distribution \(F_n (x)\) approaches its mean \(F (x)\). And, that's why the argument for rejecting the null hypothesis if there is, at any point x, a large difference between the empirical distribution \(F_n (x)\) and the hypothesized distribution \(F_0 (x)\). Not a mathematically rigorous argument, but an argument nonetheless!
Notice that the Kolmogorov-Smirnov (KS) test statistic is the supremum over all real \(x\)---a very large set of numbers! How then can we possibly hope to compute it? Well, fortunately, we don't have to check it at every real number but only at the sample values, since they are the only points at which the supremum can occur. Here's why:
First the easy case. If \(x\ge y_n\), then \(F_n(x)=1\), and the largest difference between \(F_n(x)\) and \(F_0(x)\) occurs at \(y_n\). Why? Because \(F_0(x)\) can never exceed 1 and will only get closer for larger \(x\) by the monotonicity of distribution functions. So, we can record the value \(F_n(y_n)-F_0(y_n)=1-F_0(y_n)\) and safely know that no other value \(x\ge y_n\) needs to be checked.
The case where \(x<y_1\) is a little trickier. Here, \(F_n(x)=0\), and the largest difference between \(F_n(x)\) and \(F_0(x)\) would occur at the largest possible \(x\) in this range for a reason similar to that above: \(F_0(x)\) can never be negative and only gets farther from 0 for larger \(x\). The trick is that there is no largest \(x\) in this range (since \(x\) is strictly less than \(y_1\) ), and we instead have to consider lefthand limits. Since \(F_0(x)\) is continuous, its limit at \(y_1\) is simply \(F_0(y_1)\). However, the lefthand limit of \(F_n(y_1)\) is 0. So, the value we record is \(F_0(y_1)-0=F_0(y_1)\), and ignore checking any other value \(x<y_1\).
Finally, the general case \(y_{k-1}\le x <y_{k}\) is a combination of the two above. If \(F_0(x)<F_n(x)\), then \(F_0(y_{k-1})\le F_0(x)<F_n(x)=F_n(y_{k-1})\), so that \(F_n(y_{k-1})-F_0(y_{k-1})\) is at least as large as \(F_n(x)-F_0(x)\) (so we don't even have to check those \(x\) values). If, however, \(F_0(x)>F_n(x)\), then the largest difference will occur at the lefthand limits at \(y_{k}\). Again, the continuity of \(F_0\) allows us to use \(F_0(y_{k})\) here, while the lefthand limit of \(F_n(y_{k})\) is actually \(F_n(y_{k-1})\). So, the value to record is \(F_0(y_{k})-F_n(y_{k-1})\), and we may disregard the other \(x\) values.
Whew! That covers all real \(x\) values and leaves us a much smaller set of values to actually check. In fact, if we introduce a value \(y_0\) such that \(F_n(y_0)=0\), then we can summarize all this exposition with the following rule:
- Rule for computing the KS test statistic:
-
For each ordered observation \(y_k\) compute the differences
\(|F_n(y_k)-F_0(y_k)|\) and \(|F_n(y_{k-1})-F_0(y_k)|\).
The largest of these is the KS test statistic.
The easiest way to manage these calculations is with a table, which we now demonstrate with two examples.
22.2 - Two Examples
22.2 - Two ExamplesExample 22-2
We observe the following n = 8 data points:
1.41 0.26 1.97 0.33 0.55 0.77 1.46 1.18
Is there any evidence to suggest that the data were not randomly sampled from a Uniform(0, 2) distribution?
Answer
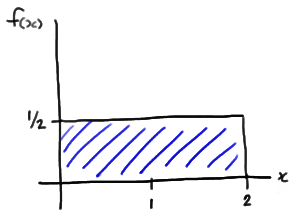
The probability density function of a Uniform(0, 2) random variable X, say, is:
\( f(x)=\frac{1}{2}\)
for 0 < x < 2. Therefore, the probability that X is less than or equal to x is:
\(P(X \le x) =\int_{0}^{x}\frac{1}{2}dt=\frac{1}{2}x\)
for 0 < x < 2, and we are interested in testing:
- the null hypothesis \(H_0 : F(x)=F_0(x)\) against
- the alternative hypothesis \(H_A : F(x) \ne F_0(x)\)
where F(x) is the (unknown) cdf from which our data were sampled, and
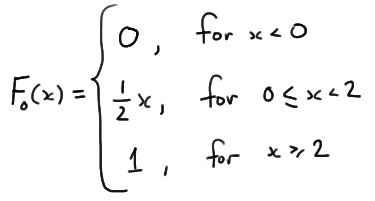
Now, in working towards calculating \(d_n\), we first need to order the eight data points so that \(y_1\le \cdots\le y_8\). The table below provides all the necessary values for finding the KS test statistic. Note that the empirical cdf satisfies \(F_n(y_k)=k/8\), for \(k=0,1,\ldots,8\).
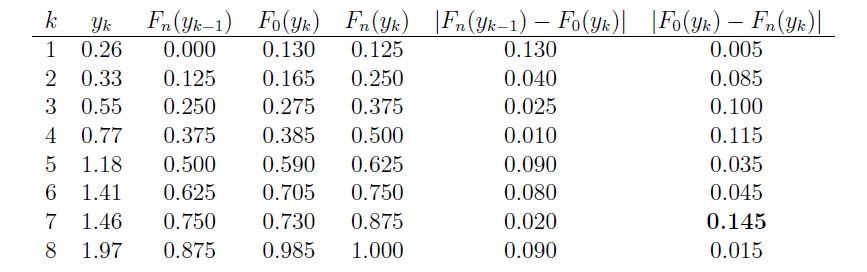
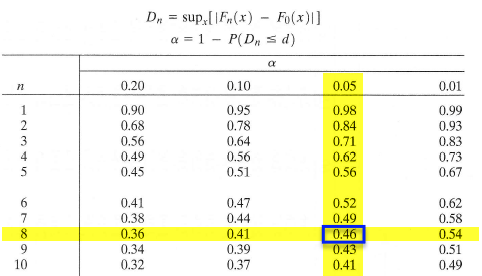
The last two columns represent all the differences we need to check. The largest of these is \(d_8=0.145\). From the table below with \(\alpha=0.05\), the critical value is \(0.46\). So, we can not reject the claim that the data were sampled from Uniform(0,2).
You might recall that the appropriateness of the t-statistic for testing the value of a population mean \(\mu\) depends on the data being normally distributed. Therefore, one of the most common applications of the Kolmogorov-Smirnov test is to see if a set of data does follow a normal distribution. Let's take a look at an example.
Example 22-3

Each person in a random sample of n = 10 employees was asked about X, the daily time wasted at work doing non-work activities, such as surfing the internet and emailing friends. The resulting data, in minutes, are as follows:
108 112 117 130 111 131 113 113 105 128
Is it okay to assume that these data come from a normal distribution with mean 120 and standard deviation 10?
Answer
We are interested in testing the null hypothesis, \(H_0:\) \(X\) is normally distributed with mean 120 and standard deviation 10, against the alternative hypothesis, \(H_A\): \(X\) is not normally distributed with mean 120 and standard deviation 10. Now, in working towards calculating \(d_n\), we again first need to order the ten data points so that \(y_1=105\), \(y_2=108\), etc. Then, we need to calculate the value of the hypothesized distribution function \(F_0(y_k)\) at each of the values of \(y_k\). The standard normal table can help us do this. The probability that \(X\) is less than or equal to 105, for example, equals the probability that \(Z\) is less than or equal to \(-1.5\):
\(F_0(y_1)=P(X\le105)=P\left(Z\le{105-120\over10}\right)=P(Z\le-1.5)=.0668.\)
The table below summarizes the relevant quantities for finding the KS test statistic. Note that the empirical cdf satisfies \(F_n(y_k)=k/10\), except at \(k=5\) because of the tie: \(y_5=y_6=113\).
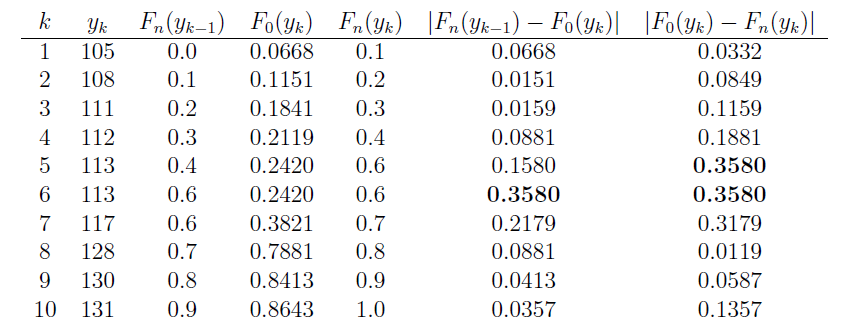
The last two columns represent all the differences we need to check. The largest of these is 0.3580. From the table below with \(\alpha=0.10\), the critical value is 0.37. Because \(d_{10} = 0.358\), which is just barely less than 0.37, we do not reject the null hypothesis at the 0.10 level. There is not enough evidence at the 0.10 level to reject the assumption that the data were randomly sampled from a normal distribution with mean 120 and standard deviation 10.

22.3 - A Confidence Band
22.3 - A Confidence BandAnother application of the Kolmogorov-Smirnov statistic is in forming a confidence band for an unknown distribution function \(F(x)\). To form a confidence band for \(F(x)\), we basically need to find a confidence interval for each value of x. The following theorem gives us the recipe for doing just that.
A \(100(1−\alpha)\%\) confidence band for the unknown distribution function \(F(x)\) is given by \(F_L(x)\) and \(F_U(x)\) where d is selected so that \(P(D_n ≥ d) = \alpha\) and:
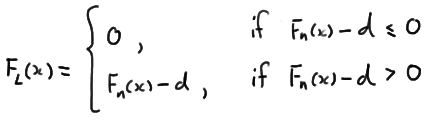
and:
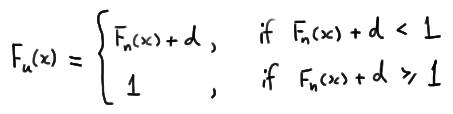
Proof
We select d so that:
\[P(D_n \ge d)=\alpha\]
Therefore, using the definition of \(D_n\), and the probability rule of complementary events, we get:
\[P(sup_x|F_n(x) -F(x)| \le d) =1-\alpha\]
Now, if the largest of the absolute values of \(F_n (x) - F(x)\) is less than or equal to d, then all of the absolute values of \(F_n (x) - F(x)\) must be less than or equal to d. That is:
\[P\left(|F_n(x) -F(x)| \le d \text{ for all } x\right) =1-\alpha\]
Rewriting the quantity inside the parentheses without the absolute value, we get:
\[P\left(-d \le F_n(x) -F(x) \le d \text{ for all } x\right) =1-\alpha\]
And, subtracting \(F_n (x)\) from each part of the resulting inequality, we get:
\[P\left(- F_n(x)-d \le -F(x) \le -F_n(x)+d \text{ for all } x\right) =1-\alpha\]
Now, when we divide through by −1, we have to switch the order of the inequality, getting:
\[P\left(F_n(x)-d \le F(x) \le F_n(x)+d \text{ for all } x\right) =1-\alpha\]
We could stop there and claim that:
\[F_n(x)-d \le F(x) \le F_n(x)+d \text{ for all } x\]
is a \(100(1−\alpha)\%\) confidence band for the unknown distribution function \(F(x)\). There's only one problem with that. It is possible that the lower limit is less than 0 and it is possible that the upper limit is greater than 1. That's not a good thing given that a distribution function must be sandwiched between 0 and 1, inclusive. We take care of that by rewriting the lower limit to prevent it from being negative:
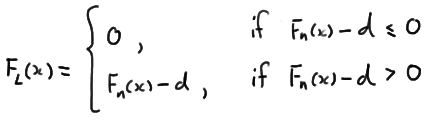
and by rewriting the upper limit to prevent it from being greater than 1:
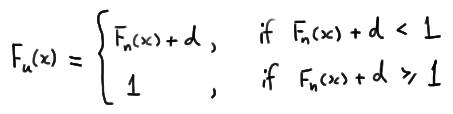
As was to be proved!
Let's try it out an example.
Example 22-4

Each person in a random sample of n = 10 employees was asked about X, the daily time wasted at work doing non-work activities, such as surfing the internet and emailing friends. The resulting data, in minutes, are as follows:
108 112 117 130 111 131 113 113 105 128
Use the data to find a 95% confidence band for the unknown cumulative distribution function \(F(x)\).
Answer
As before, we start by ordering the x values. The formulas for the lower and upper confidence limits tell us that we need to know d and \(F_n (x)\) for each of the 10 data points. Because the \(\alpha\)-level is 0.05 and the sample size n is 10, the table of Kolmogorv-Smirnov Acceptance Limits in the back of our text book, that is, Table VIII, tells us that \(d = 0.41\). We already calculated \(F_n (x)\) in the previous example.
Now, in calculating the lower limit, \(F_L(x) = F_n (x) − d = F_n (x)−0.41\), we see that the lower limit would be negative for the first four data points:
0.1−0.41 = −0.31 and 0.2−0.41 = −0.21 and 0.3−0.41 = −0.11 and 0.4−0.41 = −0.01
Therefore, we assign the first four data points a lower limit of 0, and then just calculate the remaining lower limit values. Similarly, in calculating the upper limit, \(F_U (x) = F_n (x) + d = F_n (x) + 0.41\), we see that the upper limit would be greater than 1 for the last six data points:
0.6+0.41 = 1.01 and 0.7+0.41 = 1.11 and 0.8+0.41 = 1.21 and 0.9+0.41 = 1.31 and 1.0+0.41 = 1.41
Therefore, we assign the last six data points an upper limit of 1, and then just calculate the remaining upper limit values. To summarize,
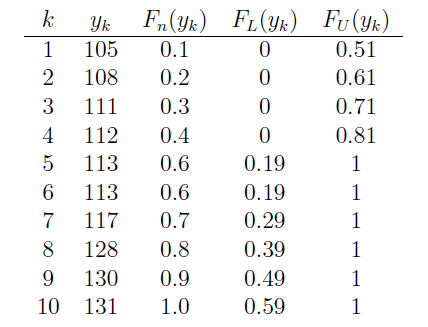
The last two columns together give us the 95% confidence band for the unknown cumulative distribution function \(F(x)\).