Lesson 24: Sufficient Statistics
Lesson 24: Sufficient StatisticsOverview
In the lesson on Point Estimation, we derived estimators of various parameters using two methods, namely, the method of maximum likelihood and the method of moments. The estimators resulting from these two methods are typically intuitive estimators. It makes sense, for example, that we would want to use the sample mean \(\bar{X}\) and sample variance \(S^2\) to estimate the mean \(\mu\) and variance \(\sigma^2\) of a normal population.
In the process of estimating such a parameter, we summarize, or reduce, the information in a sample of size \(n\), \(X_1, X_2,\ldots, X_n\), to a single number, such as the sample mean \(\bar{X}\). The actual sample values are no longer important to us. That is, if we use a sample mean of 3 to estimate the population mean \(\mu\), it doesn't matter if the original data values were (1, 3, 5) or (2, 3, 4). Has this process of reducing the \(n\) data points to a single number retained all of the information about \(\mu\) that was contained in the original \(n\) data points? Or has some information about the parameter been lost through the process of summarizing the data? In this lesson, we'll learn how to find statistics that summarize all of the information in a sample about the desired parameter. Such statistics are called sufficient statistics, and hence the name of this lesson.
Objectives
- To learn a formal definition of sufficiency.
- To learn how to apply the Factorization Theorem to identify a sufficient statistic.
- To learn how to apply the Exponential Criterion to identify a sufficient statistic.
- To extend the definition of sufficiency for one parameter to two (or more) parameters.
24.1 - Definition of Sufficiency
24.1 - Definition of SufficiencySufficiency is the kind of topic in which it is probably best to just jump right in and state its definition. Let's do that!
- Sufficient
-
Let \(X_1, X_2, \ldots, X_n\) be a random sample from a probability distribution with unknown parameter \(\theta\). Then, the statistic:
\(Y = u(X_1, X_2, ... , X_n) \)
is said to be sufficient for \(\theta\) if the conditional distribution of \(X_1, X_2, \ldots, X_n\), given the statistic \(Y\), does not depend on the parameter \(\theta\).
Example 24-1

Let \(X_1, X_2, \ldots, X_n\) be a random sample of \(n\) Bernoulli trials in which:
- \(X_i=1\) if the \(i^{th}\) subject likes Pepsi
- \(X_i=0\) if the \(i^{th}\) subject does not like Pepsi
If \(p\) is the probability that subject \(i\) likes Pepsi, for \(i = 1, 2,\ldots,n\), then:
- \(X_i=1\) with probability \(p\)
- \(X_i=0\) with probability \(q = 1 − p\)
Suppose, in a random sample of \(n=40\) people, that \(Y = \sum_{i=1}^{n}X_i =22\) people like Pepsi. If we know the value of \(Y\), the number of successes in \(n\) trials, can we gain any further information about the parameter \(p\) by considering other functions of the data \(X_1, X_2, \ldots, X_n\)? That is, is \(Y\) sufficient for \(p\)?
Answer
The definition of sufficiency tells us that if the conditional distribution of \(X_1, X_2, \ldots, X_n\), given the statistic \(Y\), does not depend on \(p\), then \(Y\) is a sufficient statistic for \(p\). The conditional distribution of \(X_1, X_2, \ldots, X_n\), given \(Y\), is by definition:
\(P(X_1 = x_1, ... , X_n = x_n |Y = y) = \dfrac{P(X_1 = x_1, ... , X_n = x_n, Y = y)}{P(Y=y)}\) (**)
Now, for the sake of concreteness, suppose we were to observe a random sample of size \(n=3\) in which \(x_1=1, x_2=0, \text{ and }x_3=1\). In this case:
\( P(X_1 = 1, X_2 = 0, X_3 =1, Y=1)=0\)
because the sum of the data values, \( \sum_{i=1}^{n}X_i \), is 1 + 0 + 1 = 2, but \(Y\), which is defined to be the sum of the \(X_i\)'s is 1. That is, because \(2\ne 1\), the event in the numerator of the starred (**) equation is an impossible event and therefore its probability is 0.
Now, let's consider an event that is possible, namely ( \(X_1=1, X_2=0, X_3=1, Y=2\)). In that case, we have, by independence:
\( P(X_1 = 1, X_2 = 0, X_3 =1, Y=2) = p(1-p) p=p^2(1-p)\)
So, in general:
\(P(X_1 = x_1, X_2 = x_2, ... , X_n = x_n, Y = y) = 0 \text{ if } \sum_{i=1}^{n}x_i \ne y \)
and:
\(P(X_1 = x_1, X_2 = x_2, ... , X_n = x_n, Y = y) = p^y(1-p)^{n-y} \text{ if } \sum_{i=1}^{n}x_i = y \)
Now, the denominator in the starred (**) equation above is the binomial probability of getting exactly \(y\) successes in \(n\) trials with a probability of success \(p\). That is, the denominator is:
\( P(Y=y) = \binom{n}{y} p^y(1-p)^{n-y}\)
for \(y = 0, 1, 2,\ldots, n\). Putting the numerator and denominator together, we get, if \(y=0, 1, 2, \ldots, n\), that the conditional probability is:
\(P(X_1 = x_1, ... , X_n = x_n |Y = y) = \dfrac{p^y(1-p)^{n-y}}{\binom{n}{y} p^y(1-p)^{n-y}} =\dfrac{1}{\binom{n}{y}} \text{ if } \sum_{i=1}^{n}x_i = y\)
and:
\(P(X_1 = x_1, ... , X_n = x_n |Y = y) = 0 \text{ if } \sum_{i=1}^{n}x_i \ne y \)
Aha! We have just shown that the conditional distribution of \(X_1, X_2, \ldots, X_n\) given \(Y\) does not depend on \(p\). Therefore, \(Y\) is indeed sufficient for \(p\). That is, once the value of \(Y\) is known, no other function of \(X_1, X_2, \ldots, X_n\) will provide any additional information about the possible value of \(p\).
24.2 - Factorization Theorem
24.2 - Factorization TheoremWhile the definition of sufficiency provided on the previous page may make sense intuitively, it is not always all that easy to find the conditional distribution of \(X_1, X_2, \ldots, X_n\) given \(Y\). Not to mention that we'd have to find the conditional distribution of \(X_1, X_2, \ldots, X_n\) given \(Y\) for every \(Y\) that we'd want to consider a possible sufficient statistic! Therefore, using the formal definition of sufficiency as a way of identifying a sufficient statistic for a parameter \(\theta\) can often be a daunting road to follow. Thankfully, a theorem often referred to as the Factorization Theorem provides an easier alternative! We state it here without proof.
- Factorization
-
Let \(X_1, X_2, \ldots, X_n\) denote random variables with joint probability density function or joint probability mass function \(f(x_1, x_2, \ldots, x_n; \theta)\), which depends on the parameter \(\theta\). Then, the statistic \(Y = u(X_1, X_2, ... , X_n) \) is sufficient for \(\theta\) if and only if the p.d.f (or p.m.f.) can be factored into two components, that is:
\(f(x_1, x_2, ... , x_n;\theta) = \phi [ u(x_1, x_2, ... , x_n);\theta ] h(x_1, x_2, ... , x_n) \)
where:
- \(\phi\) is a function that depends on the data \(x_1, x_2, \ldots, x_n\) only through the function \(u(x_1, x_2, \ldots, x_n)\), and
- the function \(h((x_1, x_2, \ldots, x_n)\) does not depend on the parameter \(\theta\)
Let's put the theorem to work on a few examples!
Example 24-2

Let \(X_1, X_2, \ldots, X_n\) denote a random sample from a Poisson distribution with parameter \(\lambda>0\). Find a sufficient statistic for the parameter \(\lambda\).
Answer
Because \(X_1, X_2, \ldots, X_n\) is a random sample, the joint probability mass function of \(X_1, X_2, \ldots, X_n\) is, by independence:
\(f(x_1, x_2, ... , x_n;\lambda) = f(x_1;\lambda) \times f(x_2;\lambda) \times ... \times f(x_n;\lambda)\)
Inserting what we know to be the probability mass function of a Poisson random variable with parameter \(\lambda\), the joint p.m.f. is therefore:
\(f(x_1, x_2, ... , x_n;\lambda) = \dfrac{e^{-\lambda}\lambda^{x_1}}{x_1!} \times\dfrac{e^{-\lambda}\lambda^{x_2}}{x_2!} \times ... \times \dfrac{e^{-\lambda}\lambda^{x_n}}{x_n!}\)
Now, simplifying, by adding up all \(n\) of the \(\lambda\)s in the exponents, as well as all \(n\) of the \(x_i\)'s in the exponents, we get:
\(f(x_1, x_2, ... , x_n;\lambda) = \left(e^{-n\lambda}\lambda^{\Sigma x_i} \right) \times \left( \dfrac{1}{x_1! x_2! ... x_n!} \right)\)
Hey, look at that! We just factored the joint p.m.f. into two functions, one (\(\phi\)) being only a function of the statistic \(Y=\sum_{i=1}^{n}X_i\) and the other (h) not depending on the parameter \(\lambda\):
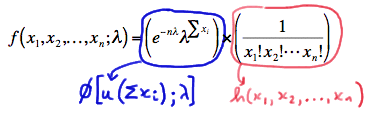
Therefore, the Factorization Theorem tells us that \(Y=\sum_{i=1}^{n}X_i\) is a sufficient statistic for \(\lambda\). But, wait a second! We can also write the joint p.m.f. as:
\(f(x_1, x_2, ... , x_n;\lambda) = \left(e^{-n\lambda}\lambda^{n\bar{x}} \right) \times \left( \dfrac{1}{x_1! x_2! ... x_n!} \right)\)
Therefore, the Factorization Theorem tells us that \(Y = \bar{X}\) is also a sufficient statistic for \(\lambda\)!
If you think about it, it makes sense that \(Y = \bar{X}\) and \(Y=\sum_{i=1}^{n}X_i\) are both sufficient statistics, because if we know \(Y = \bar{X}\), we can easily find \(Y=\sum_{i=1}^{n}X_i\). And, if we know \(Y=\sum_{i=1}^{n}X_i\), we can easily find \(Y = \bar{X}\).
The previous example suggests that there can be more than one sufficient statistic for a parameter \(\theta\). In general, if \(Y\) is a sufficient statistic for a parameter \(\theta\), then every one-to-one function of \(Y\) not involving \(\theta\) is also a sufficient statistic for \(\theta\). Let's take a look at another example.
Example 24-3

Let \(X_1, X_2, \ldots, X_n\) be a random sample from a normal distribution with mean \(\mu\) and variance 1. Find a sufficient statistic for the parameter \(\mu\).
Answer
Because \(X_1, X_2, \ldots, X_n\) is a random sample, the joint probability density function of \(X_1, X_2, \ldots, X_n\) is, by independence:
\(f(x_1, x_2, ... , x_n;\mu) = f(x_1;\mu) \times f(x_2;\mu) \times ... \times f(x_n;\mu)\)
Inserting what we know to be the probability density function of a normal random variable with mean \(\mu\) and variance 1, the joint p.d.f. is:
\(f(x_1, x_2, ... , x_n;\mu) = \dfrac{1}{(2\pi)^{1/2}} exp \left[ -\dfrac{1}{2}(x_1 - \mu)^2 \right] \times \dfrac{1}{(2\pi)^{1/2}} exp \left[ -\dfrac{1}{2}(x_2 - \mu)^2 \right] \times ... \times \dfrac{1}{(2\pi)^{1/2}} exp \left[ -\dfrac{1}{2}(x_n - \mu)^2 \right] \)
Collecting like terms, we get:
\(f(x_1, x_2, ... , x_n;\mu) = \dfrac{1}{(2\pi)^{n/2}} exp \left[ -\dfrac{1}{2}\sum_{i=1}^{n}(x_i - \mu)^2 \right]\)
A trick to making the factoring of the joint p.d.f. an easier task is to add 0 to the quantity in parentheses in the summation. That is:
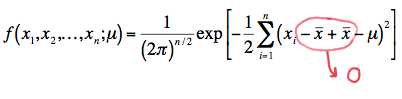
Now, squaring the quantity in parentheses, we get:
\(f(x_1, x_2, ... , x_n;\mu) = \dfrac{1}{(2\pi)^{n/2}} exp \left[ -\dfrac{1}{2}\sum_{i=1}^{n}\left[ (x_i - \bar{x})^2 +2(x_i - \bar{x}) (\bar{x}-\mu)+ (\bar{x}-\mu)^2\right] \right]\)
And then distributing the summation, we get:
\(f(x_1, x_2, ... , x_n;\mu) = \dfrac{1}{(2\pi)^{n/2}} exp \left[ -\dfrac{1}{2}\sum_{i=1}^{n} (x_i - \bar{x})^2 - (\bar{x}-\mu) \sum_{i=1}^{n}(x_i - \bar{x}) -\dfrac{1}{2}\sum_{i=1}^{n}(\bar{x}-\mu)^2\right] \)
But, the middle term in the exponent is 0, and the last term, because it doesn't depend on the index \(i\), can be added up \(n\) times:
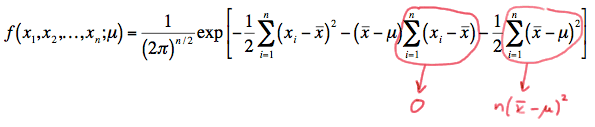
So, simplifying, we get:
\(f(x_1, x_2, ... , x_n;\mu) = \left\{ exp \left[ -\dfrac{n}{2} (\bar{x}-\mu)^2 \right] \right\} \times \left\{ \dfrac{1}{(2\pi)^{n/2}} exp \left[ -\dfrac{1}{2}\sum_{i=1}^{n} (x_i - \bar{x})^2 \right] \right\} \)
In summary, we have factored the joint p.d.f. into two functions, one (\(\phi\)) being only a function of the statistic \(Y = \bar{X}\) and the other (h) not depending on the parameter \(\mu\):
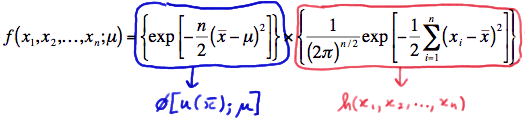
Therefore, the Factorization Theorem tells us that \(Y = \bar{X}\) is a sufficient statistic for \(\mu\). Now, \(Y = \bar{X}^3\) is also sufficient for \(\mu\), because if we are given the value of \( \bar{X}^3\), we can easily get the value of \(\bar{X}\) through the one-to-one function \(w=y^{1/3}\). That is:
\( W=(\bar{X}^3)^{1/3}=\bar{X} \)
On the other hand, \(Y = \bar{X}^2\) is not a sufficient statistic for \(\mu\), because it is not a one-to-one function. That is, if we are given the value of \(\bar{X}^2\), using the inverse function:
\(w=y^{1/2}\)
we get two possible values, namely:
\(-\bar{X}\) and \(+\bar{X}\)
We're getting so good at this, let's take a look at one more example!
Example 24-4
Let \(X_1, X_2, \ldots, X_n\) be a random sample from an exponential distribution with parameter \(\theta\). Find a sufficient statistic for the parameter \(\theta\).
Answer
Because \(X_1, X_2, \ldots, X_n\) is a random sample, the joint probability density function of \(X_1, X_2, \ldots, X_n\) is, by independence:
\(f(x_1, x_2, ... , x_n;\theta) = f(x_1;\theta) \times f(x_2;\theta) \times ... \times f(x_n;\theta)\)
Inserting what we know to be the probability density function of an exponential random variable with parameter \(\theta\), the joint p.d.f. is:
\(f(x_1, x_2, ... , x_n;\theta) =\dfrac{1}{\theta}exp\left( \dfrac{-x_1}{\theta}\right) \times \dfrac{1}{\theta}exp\left( \dfrac{-x_2}{\theta}\right) \times ... \times \dfrac{1}{\theta}exp\left( \dfrac{-x_n}{\theta} \right) \)
Now, simplifying, by adding up all \(n\) of the \(\theta\)s and the \(n\) \(x_i\)'s in the exponents, we get:
\(f(x_1, x_2, ... , x_n;\theta) =\dfrac{1}{\theta^n}exp\left( - \dfrac{1}{\theta} \sum_{i=1}^{n} x_i\right) \)
We have again factored the joint p.d.f. into two functions, one (\(\phi\)) being only a function of the statistic \(Y=\sum_{i=1}^{n}X_i\) and the other (h) not depending on the parameter \(\theta\):
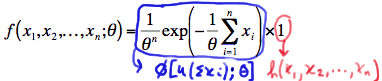
Therefore, the Factorization Theorem tells us that \(Y=\sum_{i=1}^{n}X_i\) is a sufficient statistic for \(\theta\). And, since \(Y = \bar{X}\) is a one-to-one function of \(Y=\sum_{i=1}^{n}X_i\), it implies that \(Y = \bar{X}\) is also a sufficient statistic for \(\theta\).
24.3 - Exponential Form
24.3 - Exponential FormYou might not have noticed that in all of the examples we have considered so far in this lesson, every p.d.f. or p.m.f. could we written in what is often called exponential form, that is:
\( f(x;\theta) =exp\left[K(x)p(\theta) + S(x) + q(\theta) \right] \)
with
- \(K(x)\) and \(S(x)\) being functions only of \(x\),
- \(p(\theta)\) and \(q(\theta)\) being functions only of the parameter \(\theta\)
- The support being free of the parameter \(\theta\).
First, we had Bernoulli random variables with p.m.f. written in exponential form as:
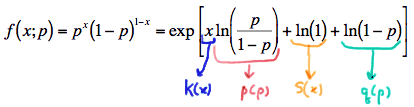
with:
- \(K(x)\) and \(S(x)\) being functions only of \(x\),
- \(p(p)\) and \(q(p)\) being functions only of the parameter \(p\)
- The support \(x=0\), 1 not depending on the parameter \(p\)
Okay, we just skipped a lot of steps in that second equality sign, that is, in getting from point A (the typical p.m.f.) to point B (the p.m.f. written in exponential form). So, let's take a look at that more closely. We start with:
\( f(x;p) =p^x(1-p)^{1-x} \)
Is the p.m.f. in exponential form? Doesn't look like it to me! We clearly need an "exp" to appear up front. The only way we are going to get that without changing the underlying function is by taking the inverse function, that is, the natural log ("ln"), at the same time. Doing so, we get:
\( f(x;p) =exp\left[\text{ln}(p^x(1-p)^{1-x}) \right] \)
Is the p.m.f. now in exponential form? Nope, not yet, but at least it's looking more hopeful. All of the steps that follow now involve using what we know about the properties of logarithms. Recognizing that the natural log of a product is the sum of the natural logs, we get:
\( f(x;p) =exp\left[\text{ln}(p^x) + \text{ln}(1-p)^{1-x} \right] \)
Is the p.m.f. now in exponential form? Nope, still not yet, because \(K(x)\), \(p(p)\), \(S(x)\), and \(q(p)\) can't yet be identified as following exponential form, but we are certainly getting closer. Recognizing that the log of a power is the power times the log of the base, we get:
\( f(x;p) =exp\left[x\text{ln}(p) + (1-x)\text{ln}(1-p) \right] \)
This is getting tiring. Is the p.m.f. in exponential form yet? Nope, afraid not yet. Let's distribute that \((1-x)\) in that last term. Doing so, we get:
\( f(x;p) =exp\left[x\text{ln}(p) + \text{ln}(1-p) - x\text{ln}(1-p) \right] \)
Is the p.m.f. now in exponential form? Let's take a closer look. Well, in the first term, we can identify the \(K(x)p(p)\) and in the middle term, we see a function that depends only on the parameter \(p\):
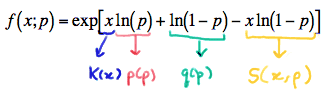
Now, all we need is the last term to depend only on \(x\) and we're as good as gold. Oh, rats! The last term depends on both \(x\) and \(p\). So back to work some more! Recognizing that the log of a quotient is the difference between the logs of the numerator and denominator, we get:
\( f(x;p) =exp\left[x\text{ln}\left( \frac{p}{1-p}\right) + \text{ln}(1-p) \right] \)
Is the p.m.f. now in exponential form? So close! Let's just add 0 in (by way of the natural log of 1) to make it obvious. Doing so, we get:
\( f(x;p) =exp\left[x\text{ln}\left( \frac{p}{1-p}\right) + \text{ln}(1) + \text{ln}(1-p) \right] \)
Yes, we have finally written the Bernoulli p.m.f. in exponential form:
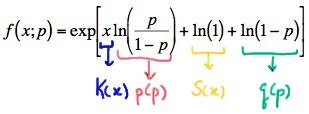
Whew! So, we've fully explored writing the Bernoulli p.m.f. in exponential form! Let's get back to reviewing all of the p.m.f.'s we've encountered in this lesson. We had Poisson random variables whose p.m.f. can be written in exponential form as:
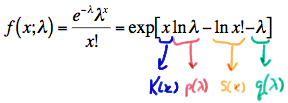
with
- \(K(x)\) and \(S(x)\) being functions only of \(x\),
- \(p(\lambda)\) and \(q(\lambda)\) being functions only of the parameter \(\lambda\)
- The support \(x = 0, 1, 2, \ldots\) not depending on the parameter \(\lambda\)
Then, we had \(N(\mu, 1)\) random variables whose p.d.f. can be written in exponential form as:
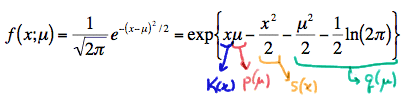
with
- \(K(x)\) and \(S(x)\) being functions only of \(x\),
- \(p(\mu)\) and \(q(\mu)\) being functions only of the parameter \(\mu\)
- The support \(-\infty<x<\infty\) not depending on the parameter \(\mu\)
Then, we had exponential random variables random variables whose p.d.f. can be written in exponential form as:
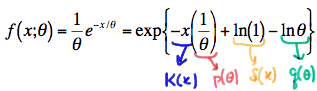
with
- \(K(x)\) and \(S(x)\) being functions only of \(x\),
- \(p(\theta)\) and \(q(\theta)\) being functions only of the parameter \(\theta\)
- The support \(x\ge 0\) not depending on the parameter \(\theta\).
Happily, it turns out that writing p.d.f.s and p.m.f.s in exponential form provides us yet a third way of identifying sufficient statistics for our parameters. The following theorem tells us how.
Exponential Criterion:
Let \(X_1, X_2, \ldots, X_n\) be a random sample from a distribution with a p.d.f. or p.m.f. of the exponential form:
\( f(x;\theta) =exp\left[K(x)p(\theta) + S(x) + q(\theta) \right] \)
with a support that does not depend on \(\theta\). Then, the statistic:
\( \sum_{i=1}^{n} K(X_i) \)
is sufficient for \(\theta\).
Proof
Because \(X_1, X_2, \ldots, X_n\) is a random sample, the joint p.d.f. (or joint p.m.f.) of \(X_1, X_2, \ldots, X_n\) is, by independence:
\(f(x_1, x_2, ... , x_n;\theta)= f(x_1;\theta) \times f(x_2;\theta) \times ... \times f(x_n;\theta) \)
Inserting what we know to be the p.m.f. or p.d.f. in exponential form, we get:
\(f(x_1, ... , x_n;\theta)=\text{exp}\left[K(x_1)p(\theta) + S(x_1)+q(\theta)\right] \times ... \times \text{exp}\left[K(x_n)p(\theta) + S(x_n)+q(\theta)\right] \)
Collecting like terms in the exponents, we get:
\(f(x_1, ... , x_n;\theta)=\text{exp}\left[p(\theta)\sum_{i=1}^{n}K(x_i) + \sum_{i=1}^{n}S(x_i) + nq(\theta)\right] \)
which can be factored as:
\(f(x_1, ... , x_n;\theta)=\left\{ \text{exp}\left[p(\theta)\sum_{i=1}^{n}K(x_i) + nq(\theta)\right]\right\} \times \left\{ \text{exp}\left[\sum_{i=1}^{n}S(x_i)\right] \right\} \)
We have factored the joint p.m.f. or p.d.f. into two functions, one (\(\phi\)) being only a function of the statistic \(Y=\sum_{i=1}^{n}K(X_i)\) and the other (h) not depending on the parameter \(\theta\):
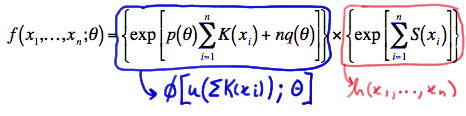
Therefore, the Factorization Theorem tells us that \(Y=\sum_{i=1}^{n}K(X_i)\) is a sufficient statistic for \(\theta\).
Let's try the Exponential Criterion out on an example.
Example 24-5

Let \(X_1, X_2, \ldots, X_n\) be a random sample from a geometric distribution with parameter \(p\). Find a sufficient statistic for the parameter \(p\).
Answer
The probability mass function of a geometric random variable is:
\(f(x;p) = (1-p)^{x-1}p\)
for \(x=1, 2, 3, \ldots\) The p.m.f. can be written in exponential form as:
\(f(x;p) = \text{exp}\left[ x\text{log}(1-p)+\text{log}(1)+\text{log}\left( \frac{p}{1-p} \right)\right] \)
Therefore, \(Y=\sum_{i=1}^{n}X_i\) is sufficient for \(p\). Easy as pie!
By the way, you might want to note that almost every p.m.f. or p.d.f. we encounter in this course can be written in exponential form. With that noted, you might want to make the Exponential Criterion the first tool you grab out of your toolbox when trying to find a sufficient statistic for a parameter.
24.4 - Two or More Parameters
24.4 - Two or More ParametersIn each of the examples we considered so far in this lesson, there is one and only one parameter. What happens if a probability distribution has two parameters, \(\theta_1\) and \(\theta_2\), say, for which we want to find sufficient statistics, \(Y_1\) and \(Y_2\)? Fortunately, the definitions of sufficiency can easily be extended to accommodate two (or more) parameters. Let's start by extending the Factorization Theorem.
- Definition (Factorization Theorem)
-
Let \(X_1, X_2, \ldots, X_n\) denote random variables with a joint p.d.f. (or joint p.m.f.):
\( f(x_1,x_2, ... ,x_n; \theta_1, \theta_2) \)
which depends on the parameters \(\theta_1\) and \(\theta_2\). Then, the statistics \(Y_1=u_1(X_1, X_2, ... , X_n)\) and \(Y_2=u_2(X_1, X_2, ... , X_n)\) are joint sufficient statistics for \(\theta_1\) and \(\theta_2\) if and only if:
\(f(x_1, x_2, ... , x_n;\theta_1, \theta_2) =\phi\left[u_1(x_1, ... , x_n), u_2(x_1, ... , x_n);\theta_1, \theta_2 \right] h(x_1, ... , x_n)\)
where:
- \(\phi\) is a function that depends on the data \((x_1, x_2, ... , x_n)\) only through the functions \(u_1(x_1, x_2, ... , x_n)\) and \(u_2(x_1, x_2, ... , x_n)\), and
- the function \(h(x_1, ... , x_n)\) does not depend on either of the parameters \(\theta_1\) or \(\theta_2\).
Let's try the extended theorem out for size on an example.
Example 24-6

Let \(X_1, X_2, \ldots, X_n\) denote a random sample from a normal distribution \(N(\theta_1, \theta_2\). That is, \(\theta_1\) denotes the mean \(\mu\) and \(\theta_2\) denotes the variance \(\sigma^2\). Use the Factorization Theorem to find joint sufficient statistics for \(\theta_1\) and \(\theta_2\).
Answer
Because \(X_1, X_2, \ldots, X_n\) is a random sample, the joint probability density function of \(X_1, X_2, \ldots, X_n\) is, by independence:
\(f(x_1, x_2, ... , x_n;\theta_1, \theta_2) = f(x_1;\theta_1, \theta_2) \times f(x_2;\theta_1, \theta_2) \times ... \times f(x_n;\theta_1, \theta_2) \times \)
Inserting what we know to be the probability density function of a normal random variable with mean \(\theta_1\) and variance \(\theta_2\), the joint p.d.f. is:
\(f(x_1, x_2, ... , x_n;\theta_1, \theta_2) = \dfrac{1}{\sqrt{2\pi\theta_2}} \text{exp} \left[-\dfrac{1}{2}\dfrac{(x_1-\theta_1)^2}{\theta_2} \right] \times ... \times = \dfrac{1}{\sqrt{2\pi\theta_2}} \text{exp} \left[-\dfrac{1}{2}\dfrac{(x_n-\theta_1)^2}{\theta_2} \right] \)
Simplifying by collecting like terms, we get:
\(f(x_1, x_2, ... , x_n;\theta_1, \theta_2) = \left(\dfrac{1}{\sqrt{2\pi\theta_2}}\right)^n \text{exp} \left[-\dfrac{1}{2}\dfrac{\sum_{i=1}^{n}(x_i-\theta_1)^2}{\theta_2} \right] \)
Rewriting the first factor, and squaring the quantity in parentheses, and distributing the summation, in the second factor, we get:
\(f(x_1, x_2, ... , x_n;\theta_1, \theta_2) = \text{exp} \left[\text{log}\left(\dfrac{1}{\sqrt{2\pi\theta_2}}\right)^n\right] \text{exp} \left[-\dfrac{1}{2\theta_2}\left\{ \sum_{i=1}^{n}x_{i}^{2} -2\theta_1\sum_{i=1}^{n}x_{i} +\sum_{i=1}^{n}\theta_{1}^{2} \right\}\right] \)
Simplifying yet more, we get:
\(f(x_1, x_2, ... , x_n;\theta_1, \theta_2) = \text{exp} \left[ -\dfrac{1}{2\theta_2}\sum_{i=1}^{n}x_{i}^{2}+\dfrac{\theta_1}{\theta_2}\sum_{i=1}^{n}x_{i} -\dfrac{n\theta_{1}^{2}}{2\theta_2}-n\text{log}\sqrt{2\pi\theta_2} \right]\)
Look at that! We have factored the joint p.d.f. into two functions, one (\(\phi\)) being only a function of the statistics \(Y_1=\sum_{i=1}^{n}X^{2}_{i}\) and \(Y_2=\sum_{i=1}^{n}X_i\), and the other (h) not depending on the parameters \(\theta_1\) and \(\theta_2\):
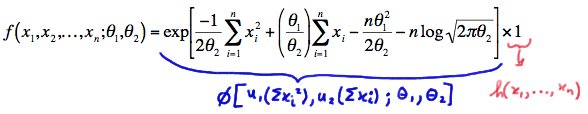
Therefore, the Factorization Theorem tells us that \(Y_1=\sum_{i=1}^{n}X^{2}_{i}\) and \(Y_2=\sum_{i=1}^{n}X_i\) are joint sufficient statistics for \(\theta_1\) and \(\theta_2\). And, the one-to-one functions of \(Y_1\) and \(Y_2\), namely:
\( \bar{X} =\dfrac{Y_2}{n}=\dfrac{1}{n}\sum_{i=1}^{n}X_i \)
and
\( S_2=\dfrac{Y_1-(Y_{2}^{2}/n)}{n-1}=\dfrac{1}{n-1} \left[\sum_{i=1}^{n}X_{i}^{2}-n\bar{X}^2 \right] \)
are also joint sufficient statistics for \(\theta_1\) and \(\theta_2\). Aha! We have just shown that the intuitive estimators of \(\mu\) and \(\sigma^2\) are also sufficient estimators. That is, the data contain no more information than the estimators \(\bar{X}\) and \(S^2\) do about the parameters \(\mu\) and \(\sigma^2\)! That seems like a good thing!
We have just extended the Factorization Theorem. Now, the Exponential Criterion can also be extended to accommodate two (or more) parameters. It is stated here without proof.
Exponential Criterion
Let \(X_1, X_2, \ldots, X_n\) be a random sample from a distribution with a p.d.f. or p.m.f. of the exponential form:
\( f(x;\theta_1,\theta_2)=\text{exp}\left[K_1(x)p_1(\theta_1,\theta_2)+K_2(x)p_2(\theta_1,\theta_2)+S(x) +q(\theta_1,\theta_2) \right] \)
with a support that does not depend on the parameters \(\theta_1\) and \(\theta_2\). Then, the statistics \(Y_1=\sum_{i=1}^{n}K_1(X_i)\) and \(Y_2=\sum_{i=1}^{n}K_2(X_i)\) are jointly sufficient for \(\theta_1\) and \(\theta_2\).
Let's try applying the extended exponential criterion to our previous example.
Example 24-6 continuted

Let \(X_1, X_2, \ldots, X_n\) denote a random sample from a normal distribution \(N(\theta_1, \theta_2)\). That is, \(\theta_1\) denotes the mean \(\mu\) and \(\theta_2\) denotes the variance \(\sigma^2\). Use the Exponential Criterion to find joint sufficient statistics for \(\theta_1\) and \(\theta_2\).
Answer
The probability density function of a normal random variable with mean \(\theta_1\) and variance \(\theta_2\) can be written in exponential form as:
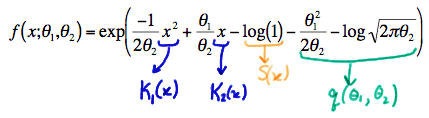
Therefore, the statistics \(Y_1=\sum_{i=1}^{n}X^{2}_{i}\) and \(Y_2=\sum_{i=1}^{n}X_i\) are joint sufficient statistics for \(\theta_1\) and \(\theta_2\).