Lesson 25: Power of a Statistical Test
Lesson 25: Power of a Statistical TestOverview
Whenever we conduct a hypothesis test, we'd like to make sure that it is a test of high quality. One way of quantifying the quality of a hypothesis test is to ensure that it is a "powerful" test. In this lesson, we'll learn what it means to have a powerful hypothesis test, as well as how we can determine the sample size n necessary to ensure that the hypothesis test we are conducting has high power.
25.1 - Definition of Power
25.1 - Definition of PowerLet's start our discussion of statistical power by recalling two definitions we learned when we first introduced to hypothesis testing:
- A Type I error occurs if we reject the null hypothesis \(H_0\) (in favor of the alternative hypothesis \(H_A\)) when the null hypothesis \(H_0\) is true. We denote \(\alpha=P(\text{Type I error})\).
- A Type II error occurs if we fail to reject the null hypothesis \(H_0\) when the alternative hypothesis \(H_A\) is true. We denote \(\beta=P(\text{Type II error})\).
You'll certainly need to know these two definitions inside and out, as you'll be thinking about them a lot in this lesson, and at any time in the future when you need to calculate a sample size either for yourself or for someone else.
Example 25-1

The Brinell hardness scale is one of several definitions used in the field of materials science to quantify the hardness of a piece of metal. The Brinell hardness measurement of a certain type of rebar used for reinforcing concrete and masonry structures was assumed to be normally distributed with a standard deviation of 10 kilograms of force per square millimeter. Using a random sample of \(n=25\) bars, an engineer is interested in performing the following hypothesis test:
- the null hypothesis \(H_0:\mu=170\)
- against the alternative hypothesis \(H_A:\mu>170\)
If the engineer decides to reject the null hypothesis if the sample mean is 172 or greater, that is, if \(\bar{X} \ge 172 \), what is the probability that the engineer commits a Type I error?
Answer
In this case, the engineer commits a Type I error if his observed sample mean falls in the rejection region, that is, if it is 172 or greater, when the true (unknown) population mean is indeed 170. Graphically, \(\alpha\), the engineer's probability of committing a Type I error looks like this:
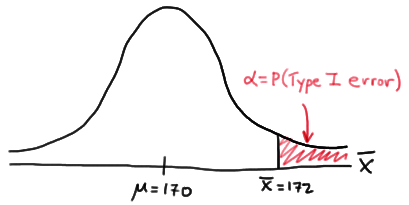
Now, we can calculate the engineer's value of \(\alpha\) by making the transformation from a normal distribution with a mean of 170 and a standard deviation of 10 to that of \(Z\), the standard normal distribution using:
\(Z= \frac{\bar{X}-\mu}{\sigma / \sqrt{n}} \)
Doing so, we get:
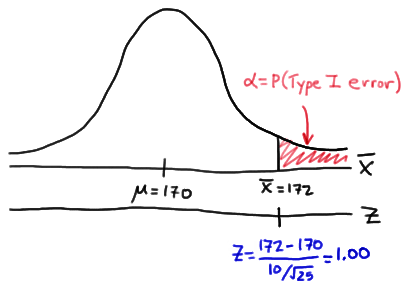
So, calculating the engineer's probability of committing a Type I error reduces to making a normal probability calculation. The probability is 0.1587 as illustrated here:
\(\alpha = P(\bar{X} \ge 172 \text { if } \mu = 170) = P(Z \ge 1.00) = 0.1587 \)
A probability of 0.1587 is a bit high. We'll learn in this lesson how the engineer could reduce his probability of committing a Type I error.
If, unknown to engineer, the true population mean were \(\mu=173\), what is the probability that the engineer commits a Type II error?
Answer
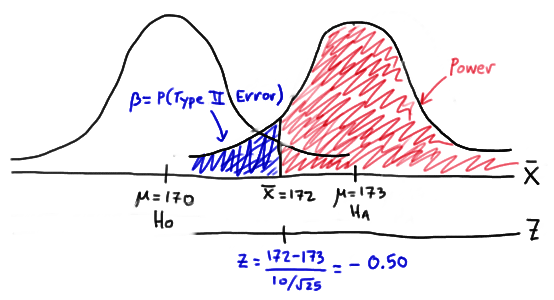
In this case, the engineer commits a Type II error if his observed sample mean does not fall in the rejection region, that is, if it is less than 172, when the true (unknown) population mean is 173. Graphically, \(\beta\), the engineer's probability of committing a Type II error looks like this:
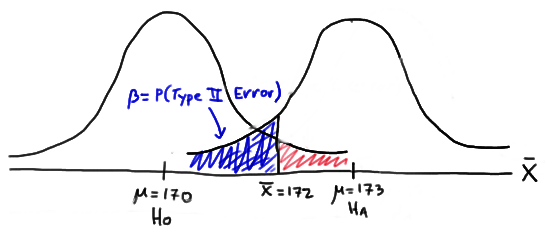
Again, we can calculate the engineer's value of \(\beta\) by making the transformation from a normal distribution with a mean of 173 and a standard deviation of 10 to that of \(Z\), the standard normal distribution. Doing so, we get:
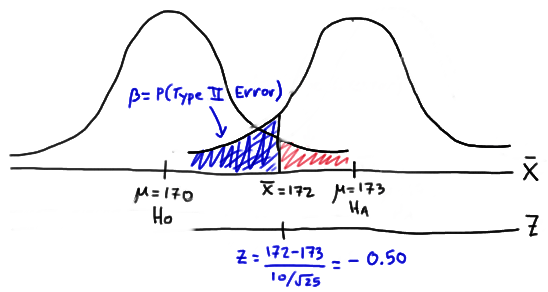
So, calculating the engineer's probability of committing a Type II error again reduces to making a normal probability calculation. The probability is 0.3085 as illustrated here:
\(\beta= P(\bar{X} < 172 \text { if } \mu = 173) = P(Z < -0.50) = 0.3085 \)
A probability of 0.3085 is a bit high. We'll learn in this lesson how the engineer could reduce his probability of committing a Type II error.
 If you think about it, considering the probability of committing a Type II error is quite similar to looking at a glass that is half empty. That is, rather than considering the probability that the engineer commits an error, perhaps we could consider the probability that the engineer makes the correct decision. Doing so, involves calculating what is called the power of the hypothesis test.
If you think about it, considering the probability of committing a Type II error is quite similar to looking at a glass that is half empty. That is, rather than considering the probability that the engineer commits an error, perhaps we could consider the probability that the engineer makes the correct decision. Doing so, involves calculating what is called the power of the hypothesis test.
- Power of the Hypothesis Test
-
The power of a hypothesis test is the probability of making the correct decision if the alternative hypothesis is true. That is, the power of a hypothesis test is the probability of rejecting the null hypothesis \(H_0\) when the alternative hypothesis \(H_A\) is the hypothesis that is true.
Let's return to our engineer's problem to see if we can instead look at the glass as being half full!
Example 25-1 (continued)
If, unknown to the engineer, the true population mean were \(\mu=173\), what is the probability that the engineer makes the correct decision by rejecting the null hypothesis in favor of the alternative hypothesis?
Answer
In this case, the engineer makes the correct decision if his observed sample mean falls in the rejection region, that is, if it is greater than 172, when the true (unknown) population mean is 173. Graphically, the power of the engineer's hypothesis test looks like this:
That makes the power of the engineer's hypothesis test 0.6915 as illustrated here:
\(\text{Power } = P(\bar{X} \ge 172 \text { if } \mu = 173) = P(Z \ge -0.50) = 0.6915 \)
which of course could have alternatively been calculated by simply subtracting the probability of committing a Type II error from 1, as shown here:
\(\text{Power } = 1 - \beta = 1 - 0.3085 = 0.6915 \)
At any rate, if the unknown population mean were 173, the engineer's hypothesis test would be at least a bit better than flipping a fair coin, in which he'd have but a 50% chance of choosing the correct hypothesis. In this case, he has a 69.15% chance. He could still do a bit better.
In general, for every hypothesis test that we conduct, we'll want to do the following:
-
Minimize the probability of committing a Type I error. That, is minimize \(\alpha=P(\text{Type I Error})\). Typically, a significance level of \(\alpha\le 0.10\) is desired.
-
Maximize the power (at a value of the parameter under the alternative hypothesis that is scientifically meaningful). Typically, we desire power to be 0.80 or greater. Alternatively, we could minimize \(\beta=P(\text{Type II Error})\), aiming for a type II error rate of 0.20 or less.
By the way, in the second point, what exactly does "at a value of the parameter under the alternative hypothesis that is scientifically meaningful" mean? Well, let's suppose that a medical researcher is interested in testing the null hypothesis that the mean total blood cholesterol in a population of patients is 200 mg/dl against the alternative hypothesis that the mean total blood cholesterol is greater than 200 mg/dl. Well, the alternative hypothesis contains an infinite number of possible values of the mean. Under the alternative hypothesis, the mean of the population could be, among other values, 201, 202, or 210. Suppose the medical researcher rejected the null hypothesis, because the mean was 201. Whoopdy-do...would that be a rocking conclusion? No, probably not. On the other hand, suppose the medical researcher rejected the null hypothesis, because the mean was 215. In that case, the mean is substantially different enough from the assumed mean under the null hypothesis, that we'd probably get excited about the result. In summary, in this example, we could probably all agree to consider a mean of 215 to be "scientifically meaningful," whereas we could not do the same for a mean of 201.
Now, of course, all of this talk is a bit if gibberish, because we'd never really know whether the true unknown population mean were 201 or 215, otherwise, we wouldn't have to be going through the process of conducting a hypothesis test about the mean. We can do something though. We can plan our scientific studies so that our hypothesis tests have enough power to reject the null hypothesis in favor of values of the parameter under the alternative hypothesis that are scientifically meaningful.
25.2 - Power Functions
25.2 - Power FunctionsExample 25-2

Let's take a look at another example that involves calculating the power of a hypothesis test.
Let \(X\) denote the IQ of a randomly selected adult American. Assume, a bit unrealistically, that \(X\) is normally distributed with unknown mean \(\mu\) and standard deviation 16. Take a random sample of \(n=16\) students, so that, after setting the probability of committing a Type I error at \(\alpha=0.05\), we can test the null hypothesis \(H_0:\mu=100\) against the alternative hypothesis that \(H_A:\mu>100\).
What is the power of the hypothesis test if the true population mean were \(\mu=108\)?
Answer
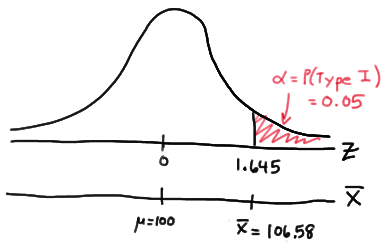
Setting \(\alpha\), the probability of committing a Type I error, to 0.05, implies that we should reject the null hypothesis when the test statistic \(Z\ge 1.645\), or equivalently, when the observed sample mean is 106.58 or greater:
because we transform the test statistic \(Z\) to the sample mean by way of:
\(Z=\dfrac{\bar{X}-\mu}{\frac{\sigma}{\sqrt{n}}}\qquad \Rightarrow \bar{X}=\mu+Z\dfrac{\sigma}{\sqrt{n}} \qquad \bar{X}=100+1.645\left(\dfrac{16}{\sqrt{16}}\right)=106.58\)
Now, that implies that the power, that is, the probability of rejecting the null hypothesis, when \(\mu=108\) is 0.6406 as calculated here (recalling that \(Phi(z)\) is standard notation for the cumulative distribution function of the standard normal random variable):
\( \text{Power}=P(\bar{X}\ge 106.58\text{ when } \mu=108) = P\left(Z\ge \dfrac{106.58-108}{\frac{16}{\sqrt{16}}}\right) \\ = P(Z\ge -0.36)=1-P(Z<-0.36)=1-\Phi(-0.36)=1-0.3594=0.6406 \)
and illustrated here:
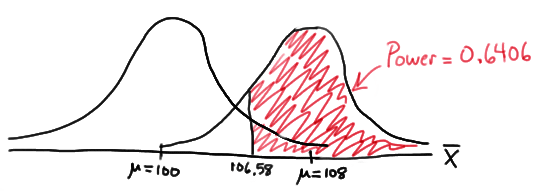
In summary, we have determined that we have (only) a 64.06% chance of rejecting the null hypothesis \(H_0:\mu=100\) in favor of the alternative hypothesis \(H_A:\mu>100\) if the true unknown population mean is in reality \(\mu=108\).
What is the power of the hypothesis test if the true population mean were \(\mu=112\)?
Answer
Because we are setting \(\alpha\), the probability of committing a Type I error, to 0.05, we again reject the null hypothesis when the test statistic \(Z\ge 1.645\), or equivalently, when the observed sample mean is 106.58 or greater. That means that the probability of rejecting the null hypothesis, when \(\mu=112\) is 0.9131 as calculated here:
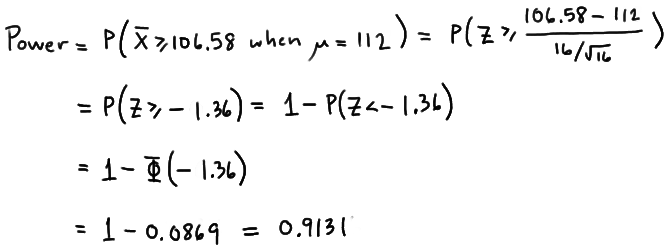
\( \text{Power}=P(\bar{X}\ge 106.58\text{ when }\mu=112)=P\left(Z\ge \frac{106.58-112}{\frac{16}{\sqrt{16}}}\right) \\ = P(Z\ge -1.36)=1-P(Z<-1.36)=1-\Phi(-1.36)=1-0.0869=0.9131 \)
and illustrated here:
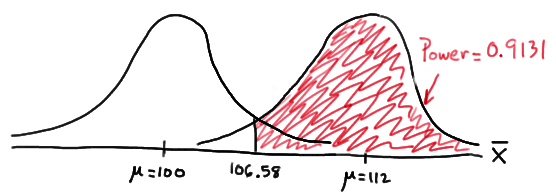
In summary, we have determined that we now have a 91.31% chance of rejecting the null hypothesis \(H_0:\mu=100\) in favor of the alternative hypothesis \(H_A:\mu>100\) if the true unknown population mean is in reality \(\mu=112\). Hmm.... it should make sense that the probability of rejecting the null hypothesis is larger for values of the mean, such as 112, that are far away from the assumed mean under the null hypothesis.
What is the power of the hypothesis test if the true population mean were \(\mu=116\)?
Answer
Again, because we are setting \(\alpha\), the probability of committing a Type I error, to 0.05, we reject the null hypothesis when the test statistic \(Z\ge 1.645\), or equivalently, when the observed sample mean is 106.58 or greater. That means that the probability of rejecting the null hypothesis, when \(\mu=116\) is 0.9909 as calculated here:
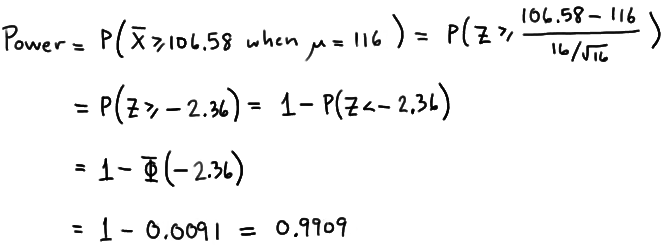
\(\text{Power}=P(\bar{X}\ge 106.58\text{ when }\mu=116) =P\left(Z\ge \dfrac{106.58-116}{\frac{16}{\sqrt{16}}}\right) = P(Z\ge -2.36)=1-P(Z<-2.36)= 1-\Phi(-2.36)=1-0.0091=0.9909 \)
and illustrated here:
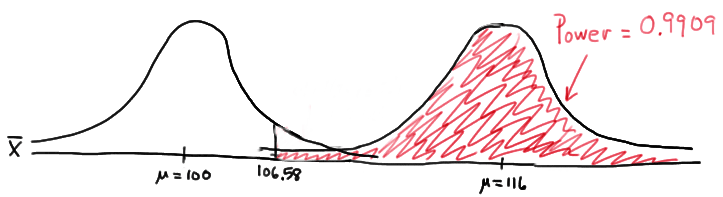
In summary, we have determined that, in this case, we have a 99.09% chance of rejecting the null hypothesis \(H_0:\mu=100\) in favor of the alternative hypothesis \(H_A:\mu>100\) if the true unknown population mean is in reality \(\mu=116\). The probability of rejecting the null hypothesis is the largest yet of those we calculated, because the mean, 116, is the farthest away from the assumed mean under the null hypothesis.
Are you growing weary of this? Let's summarize a few things we've learned from engaging in this exercise:
- First and foremost, my instructor can be tedious at times..... errrr, I mean, first and foremost, the power of a hypothesis test depends on the value of the parameter being investigated. In the above, example, the power of the hypothesis test depends on the value of the mean \(\mu\).
- As the actual mean \(\mu\) moves further away from the value of the mean \(\mu=100\) under the null hypothesis, the power of the hypothesis test increases.
It's that first point that leads us to what is called the power function of the hypothesis test. If you go back and take a look, you'll see that in each case our calculation of the power involved a step that looks like this:
\(\text{Power } =1 - \Phi (z) \) where \(z = \frac{106.58 - \mu}{16 / \sqrt{16}} \)
That is, if we use the standard notation \(K(\mu)\) to denote the power function, as it depends on \(\mu\), we have:
\(K(\mu) = 1- \Phi \left( \frac{106.58 - \mu}{16 / \sqrt{16}} \right) \)
So, the reality is your instructor could have been a whole lot more tedious by calculating the power for every possible value of \(\mu\) under the alternative hypothesis! What we can do instead is create a plot of the power function, with the mean \(\mu\) on the horizontal axis and the power \(K(\mu)\) on the vertical axis. Doing so, we get a plot in this case that looks like this:
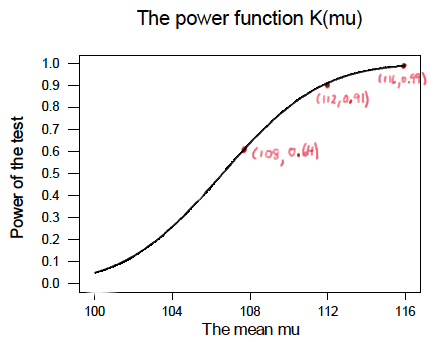
Now, what can we learn from this plot? Well:
-
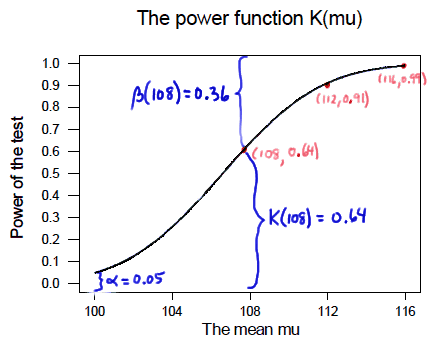
We can see that \(\alpha\) (the probability of a Type I error), \(\beta\) (the probability of a Type II error), and \(K(\mu)\) are all represented on a power function plot, as illustrated here:
-
We can see that the probability of a Type I error is \(\alpha=K(100)=0.05\), that is, the probability of rejecting the null hypothesis when the null hypothesis is true is 0.05.
-
We can see the power of a test \(K(\mu)\), as well as the probability of a Type II error \(\beta(\mu)\), for each possible value of \(\mu\).
-
We can see that \(\beta(\mu)=1-K(\mu)\) and vice versa, that is, \(K(\mu)=1-\beta(\mu)\).
-
And we can see graphically that, indeed, as the actual mean \(\mu\) moves further away from the null mean \(\mu=100\), the power of the hypothesis test increases.
Now, what would do you suppose would happen to the power of our hypothesis test if we were to change our willingness to commit a Type I error? Would the power for a given value of \(\mu\) increase, decrease, or remain unchanged? Suppose, for example, that we wanted to set \(\alpha=0.01\) instead of \(\alpha=0.05\)? Let's return to our example to explore this question.
Example 25-2 (continued)

Let \(X\) denote the IQ of a randomly selected adult American. Assume, a bit unrealistically, that \(X\) is normally distributed with unknown mean \(\mu\) and standard deviation 16. Take a random sample of \(n=16\) students, so that, after setting the probability of committing a Type I error at \(\alpha=0.01\), we can test the null hypothesis \(H_0:\mu=100\) against the alternative hypothesis that \(H_A:\mu>100\).
What is the power of the hypothesis test if the true population mean were \(\mu=108\)?
Answer
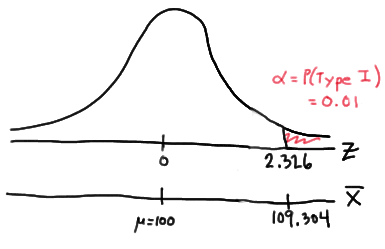
Setting \(\alpha\), the probability of committing a Type I error, to 0.01, implies that we should reject the null hypothesis when the test statistic \(Z\ge 2.326\), or equivalently, when the observed sample mean is 109.304 or greater:
because:
\(\bar{x} = \mu + z \left( \frac{\sigma}{\sqrt{n}} \right) =100 + 2.326\left( \frac{16}{\sqrt{16}} \right)=109.304 \)
That means that the probability of rejecting the null hypothesis, when \(\mu=108\) is 0.3722 as calculated here:
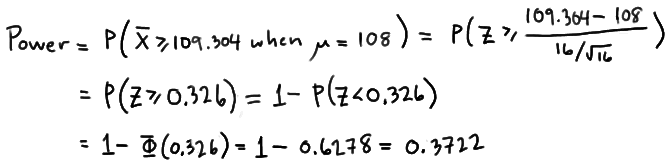
So, the power when \(\mu=108\) and \(\alpha=0.01\) is smaller (0.3722) than the power when \(\mu=108\) and \(\alpha=0.05\) (0.6406)! Perhaps we can see this graphically:
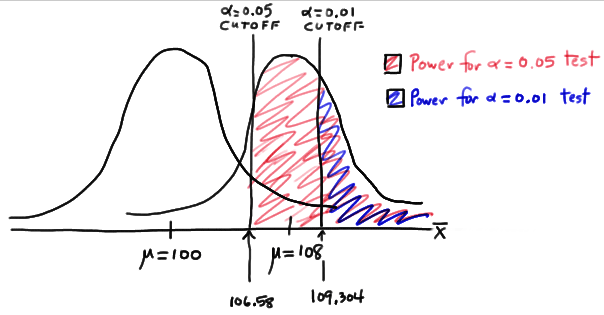
By the way, we could again alternatively look at the glass as being half-empty. In that case, the probability of a Type II error when \(\mu=108\) and \(\alpha=0.01\) is \(1-0.3722=0.6278\). In this case, the probability of a Type II error is greater than the probability of a Type II error when \(\mu=108\) and \(\alpha=0.05\).
All of this can be seen graphically by plotting the two power functions, one where \(\alpha=0.01\) and the other where \(\alpha=0.05\), simultaneously. Doing so, we get a plot that looks like this:
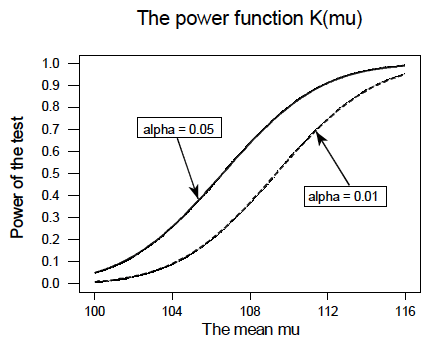
This last example illustrates that, providing the sample size \(n\) remains unchanged, a decrease in \(\alpha\) causes an increase in \(\beta\), and at least theoretically, if not practically, a decrease in \(\beta\) causes an increase in \(\alpha\). It turns out that the only way that \(\alpha\) and \(\beta\) can be decreased simultaneously is by increasing the sample size \(n\).
25.3 - Calculating Sample Size
25.3 - Calculating Sample SizeBefore we learn how to calculate the sample size that is necessary to achieve a hypothesis test with a certain power, it might behoove us to understand the effect that sample size has on power. Let's investigate by returning to our IQ example.
Example 25-3
Let \(X\) denote the IQ of a randomly selected adult American. Assume, a bit unrealistically again, that \(X\) is normally distributed with unknown mean \(\mu\) and (a strangely known) standard deviation of 16. This time, instead of taking a random sample of \(n=16\) students, let's increase the sample size to \(n=64\). And, while setting the probability of committing a Type I error to \(\alpha=0.05\), test the null hypothesis \(H_0:\mu=100\) against the alternative hypothesis that \(H_A:\mu>100\).
What is the power of the hypothesis test when \(\mu=108\), \(\mu=112\), and \(\mu=116\)?
Answer
Setting \(\alpha\), the probability of committing a Type I error, to 0.05, implies that we should reject the null hypothesis when the test statistic \(Z\ge 1.645\), or equivalently, when the observed sample mean is 103.29 or greater:
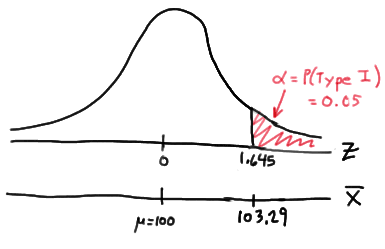
because:
\( \bar{x} = \mu + z \left(\dfrac{\sigma}{\sqrt{n}} \right) = 100 +1.645\left(\dfrac{16}{\sqrt{64}} \right) = 103.29\)
Therefore, the power function \K(\mu)\), when \(\mu>100\) is the true value, is:
\( K(\mu) = P(\bar{X} \ge 103.29 | \mu) = P \left(Z \ge \dfrac{103.29 - \mu}{16 / \sqrt{64}} \right) = 1 - \Phi \left(\dfrac{103.29 - \mu}{2} \right)\)
Therefore, the probability of rejecting the null hypothesis at the \(\alpha=0.05\) level when \(\mu=108\) is 0.9907, as calculated here:
\(K(108) = 1 - \Phi \left( \dfrac{103.29-108}{2} \right) = 1- \Phi(-2.355) = 0.9907 \)
And, the probability of rejecting the null hypothesis at the \(\alpha=0.05\) level when \(\mu=112\) is greater than 0.9999, as calculated here:
\( K(112) = 1 - \Phi \left( \dfrac{103.29-112}{2} \right) = 1- \Phi(-4.355) = 0.9999\ldots \)
And, the probability of rejecting the null hypothesis at the \(\alpha=0.05\) level when \(\mu=116\) is greater than 0.999999, as calculated here:
\( K(116) = 1 - \Phi \left( \dfrac{103.29-116}{2} \right) = 1- \Phi(-6.355) = 0.999999... \)
In summary, in the various examples throughout this lesson, we have calculated the power of testing \(H_0:\mu=100\) against \(H_A:\mu>100\) for two sample sizes ( \(n=16\) and \(n=64\)) and for three possible values of the mean ( \(\mu=108\), \(\mu=112\), and \(\mu=116\)). Here's a summary of our power calculations:

As you can see, our work suggests that for a given value of the mean \(\mu\) under the alternative hypothesis, the larger the sample size \(n\), the greater the power \(K(\mu)\). Perhaps there is no better way to see this than graphically by plotting the two power functions simultaneously, one when \(n=16\) and the other when \(n=64\):
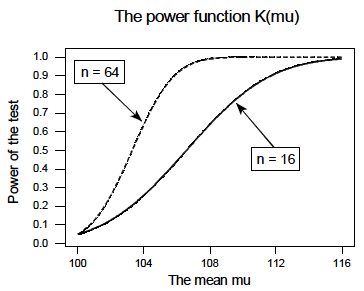
As this plot suggests, if we are interested in increasing our chance of rejecting the null hypothesis when the alternative hypothesis is true, we can do so by increasing our sample size \(n\). This benefit is perhaps even greatest for values of the mean that are close to the value of the mean assumed under the null hypothesis. Let's take a look at two examples that illustrate the kind of sample size calculation we can make to ensure our hypothesis test has sufficient power.
Example 25-4

Let \(X\) denote the crop yield of corn measured in the number of bushels per acre. Assume (unrealistically) that \(X\) is normally distributed with unknown mean \(\mu\) and standard deviation \(\sigma=6\). An agricultural researcher is working to increase the current average yield from 40 bushels per acre. Therefore, he is interested in testing, at the \(\alpha=0.05\) level, the null hypothesis \(H_0:\mu=40\) against the alternative hypothesis that \(H_A:\mu>40\). Find the sample size \(n\) that is necessary to achieve 0.90 power at the alternative \(\mu=45\).
Answer
As is always the case, we need to start by finding a threshold value \(c\), such that if the sample mean is larger than \(c\), we'll reject the null hypothesis:
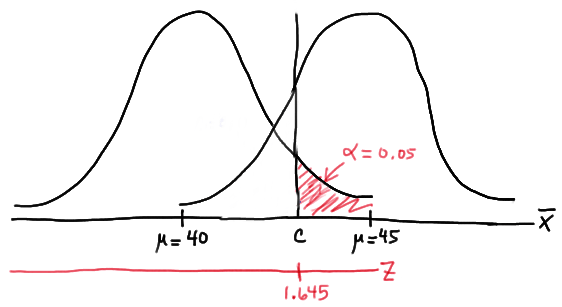
That is, in order for our hypothesis test to be conducted at the \(\alpha=0.05\) level, the following statement must hold (using our typical \(Z\) transformation):
\(c = 40 + 1.645 \left( \dfrac{6}{\sqrt{n}} \right) \) (**)
But, that's not the only condition that \(c\) must meet, because \(c\) also needs to be defined to ensure that our power is 0.90 or, alternatively, that the probability of a Type II error is 0.10. That would happen if there was a 10% chance that our test statistic fell short of \(c\) when \(\mu=45\), as the following drawing illustrates in blue:
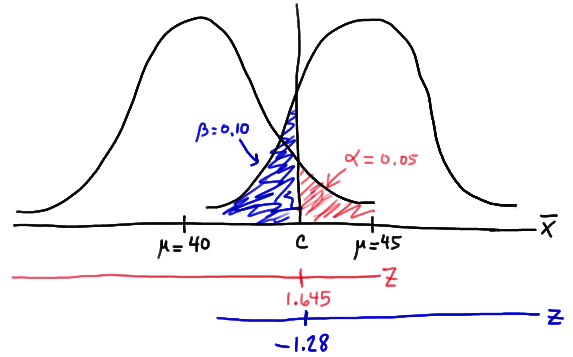
This illustration suggests that in order for our hypothesis test to have 0.90 power, the following statement must hold (using our usual \(Z\) transformation):
\(c = 45 - 1.28 \left( \dfrac{6}{\sqrt{n}} \right) \) (**)
Aha! We have two (asterisked (**)) equations and two unknowns! All we need to do is equate the equations, and solve for \(n\). Doing so, we get:
\(40+1.645\left(\frac{6}{\sqrt{n}}\right)=45-1.28\left(\frac{6}{\sqrt{n}}\right)\)
\(\Rightarrow 5=(1.645+1.28)\left(\frac{6}{\sqrt{n}}\right), \qquad \Rightarrow 5=\frac{17.55}{\sqrt{n}}, \qquad n=(3.51)^2=12.3201\approx 13\)
Now that we know we will set \(n=13\), we can solve for our threshold value c:
\( c = 40 + 1.645 \left( \dfrac{6}{\sqrt{13}} \right)=42.737 \)
So, in summary, if the agricultural researcher collects data on \(n=13\) corn plots, and rejects his null hypothesis \(H_0:\mu=40\) if the average crop yield of the 13 plots is greater than 42.737 bushels per acre, he will have a 5% chance of committing a Type I error and a 10% chance of committing a Type II error if the population mean \(\mu\) were actually 45 bushels per acre.
Example 25-5

Consider \(p\), the true proportion of voters who favor a particular political candidate. A pollster is interested in testing at the \(\alpha=0.01\) level, the null hypothesis \(H_0:9=0.5\) against the alternative hypothesis that \(H_A:p>0.5\). Find the sample size \(n\) that is necessary to achieve 0.80 power at the alternative \(p=0.55\).
Answer
In this case, because we are interested in performing a hypothesis test about a population proportion \(p\), we use the \(Z\)-statistic:
\(Z = \dfrac{\hat{p}-p_0}{\sqrt{\frac{p_0(1-p_0)}{n}}} \)
Again, we start by finding a threshold value \(c\), such that if the observed sample proportion is larger than \(c\), we'll reject the null hypothesis:
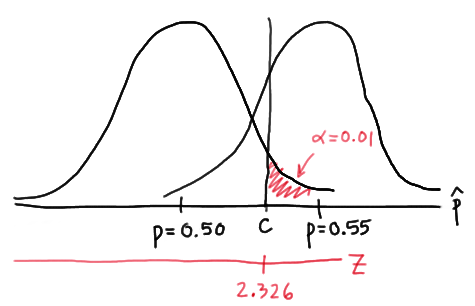
That is, in order for our hypothesis test to be conducted at the \(\alpha=0.01\) level, the following statement must hold:
\(c = 0.5 + 2.326 \sqrt{ \dfrac{(0.5)(0.5)}{n}} \) (**)
But, again, that's not the only condition that c must meet, because \(c\) also needs to be defined to ensure that our power is 0.80 or, alternatively, that the probability of a Type II error is 0.20. That would happen if there was a 20% chance that our test statistic fell short of \(c\) when \(p=0.55\), as the following drawing illustrates in blue:
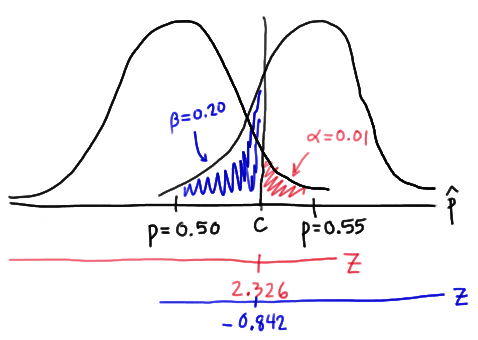
This illustration suggests that in order for our hypothesis test to have 0.80 power, the following statement must hold:
\(c = 0.55 - 0.842 \sqrt{ \dfrac{(0.55)(0.45)}{n}} \) (**)
Again, we have two (asterisked (**)) equations and two unknowns! All we need to do is equate the equations, and solve for \(n\). Doing so, we get:
\(0.5+2.326\sqrt{\dfrac{0.5(0.5)}{n}}=0.55-0.842\sqrt{\dfrac{0.55(0.45)}{n}} \\ 2.326\dfrac{\sqrt{0.25}}{\sqrt{n}}+0.842\dfrac{\sqrt{0.2475}}{\sqrt{n}}=0.55-0.5 \\ \dfrac{1}{\sqrt{n}}(1.5818897)=0.05 \qquad \Rightarrow n\approx \left(\dfrac{1.5818897}{0.05}\right)^2 = 1000.95 \approx 1001 \)
Now that we know we will set \(n=1001\), we can solve for our threshold value \(c\):
\(c = 0.5 + 2.326 \sqrt{\dfrac{(0.5)(0.5)}{1001}}= 0.5367 \)
So, in summary, if the pollster collects data on \(n=1001\) voters, and rejects his null hypothesis \(H_0:p=0.5\) if the proportion of sampled voters who favor the political candidate is greater than 0.5367, he will have a 1% chance of committing a Type I error and a 20% chance of committing a Type II error if the population proportion \(p\) were actually 0.55.
Incidentally, we can always check our work! Conducting the survey and subsequent hypothesis test as described above, the probability of committing a Type I error is:
\(\alpha= P(\hat{p} >0.5367 \text { if } p = 0.50) = P(Z > 2.3257) = 0.01 \)
and the probability of committing a Type II error is:
\(\beta = P(\hat{p} <0.5367 \text { if } p = 0.55) = P(Z < -0.846) = 0.199 \)
just as the pollster had desired.
We've illustrated several sample size calculations. Now, let's summarize the information that goes into a sample size calculation. In order to determine a sample size for a given hypothesis test, you need to specify:
-
The desired \(\alpha\) level, that is, your willingness to commit a Type I error.
-
The desired power or, equivalently, the desired \(\beta\) level, that is, your willingness to commit a Type II error.
-
A meaningful difference from the value of the parameter that is specified in the null hypothesis.
-
The standard deviation of the sample statistic or, at least, an estimate of the standard deviation (the "standard error") of the sample statistic.