Lesson 7: Simple Linear Regression
Lesson 7: Simple Linear RegressionOverview

Simple linear regression is a way of evaluating the relationship between two continuous variables. One variable is regarded as the predictor variable, explanatory variable, or independent variable \((x)\). The other variable is regarded as the response variable, outcome variable, or dependent variable \((y)\).
For example, we might we interested in investigating the (linear?) relationship between:
- heights and weights
- high school grade point averages and college grade point averages
- speed and gas mileage
- outdoor temperature and evaporation rate
- the Dow Jones industrial average and the consumer confidence index
7.1 - Types of Relationships
7.1 - Types of RelationshipsBefore we dig into the methods of simple linear regression, we need to distinguish between two different type of relationships, namely:
- deterministic relationships
- statistical relationships
As we'll soon see, simple linear regression concerns statistical relationships.
Deterministic (or Functional) Relationships
A deterministic (or functional) relationship is an exact relationship between the predictor \(x\) and the response \(y\). Take, for instance, the conversion relationship between temperature in degrees Celsius \((C)\) and temperature in degrees Fahrenheit \((F)\). We know the relationship is:
\(F=\dfrac{9}{5}C+32\)
Therefore, if we know that it is 10 degrees Celsius, we also know that it is 50 degrees Fahrenheit:
\(F=\dfrac{9}{5}(10)+32=50\)
This is what the exact (linear) relationship between degrees Celsius and degrees Fahrenheit looks like graphically:
Other examples of deterministic relationships include the relationship between the diameter \((d)\) and circumference of a circle \((C)\):
\(C=\pi \times d\)
the relationship between the applied weight \((X)\) and the amount of stretch in a spring \((Y)\) (known as Hooke's Law):
\(Y=\alpha+\beta X\)
the relationship between the voltage applied \((V)\), the resistance \((r)\) and the current \((I)\) (known as Ohm's Law):
\(I=\dfrac{V}{r}\)
and, for a constant temperature, the relationship between pressure \((P)\) and volume of gas \((V)\) (known as Boyle's Law):
\(P=\dfrac{\alpha}{V}\)
where \(\alpha\) is a known constant for each gas.
Statistical Relationships
A statistical relationship, on the other hand, is not an exact relationship. It is instead a relationship in which "trend" exists between the predictor \(x\) and the response \(y\), but there is also some "scatter." Here's a graph illustrating how a statistical relationship might look:
In this case, researchers investigated the relationship between the latitude (in degrees) at the center of each of the 50 U.S. states and the mortality (in deaths per 10 million) due to skin cancer in each of the 50 U.S. states. Perhaps we shouldn't be surprised to see a downward trend, but not an exact relationship, between latitude and skin cancer mortality. That is, as the latitude increases for the northern states, in which sun exposure is less prevalent and less intense, mortality due to skin cancer decreases, but not perfectly so.
Other examples of statistical relationships include:
- the positive relationship between height and weight
- the positive relationship between alcohol consumed and blood alcohol content
- the negative relationship between vital lung capacity and pack-years of smoking
- the negative relationship between driving speed and gas mileage
It is these type of less-than-perfect statistical relationships that we are interested in when we investigate the methods of simple linear regression.
7.2 - Least Squares: The Idea
7.2 - Least Squares: The IdeaExample 7-1
Before delving into the theory of least squares, let's motivate the idea behind the method of least squares by way of example.
A student was interested in quantifying the (linear) relationship between height (in inches) and weight (in pounds), so she measured the height and weight of ten randomly selected students in her class. After taking the measurements, she created the adjacent scatterplot of the obtained heights and weights. Wanting to summarize the relationship between height and weight, she eyeballed what she thought were two good lines (solid and dashed), but couldn't decide between:
- \(\text{weight} = −266.5 + 6.1\times \text{height}\)
- \(\text{weight} = −331.2 + 7.1\times \text{height}\)
Which is the "best fitting line"?
Answer
In order to facilitate finding the best fitting line, let's define some notation. Recalling that an experimental unit is the thing being measured (in this case, a student):
- let \(y_i\) denote the observed response for the \(i^{th}\) experimental unit
- let \(x_i\) denote the predictor value for the \(i^{th}\) experimental unit
- let \(\hat{y}_i\) denote the predicted response (or fitted value) for the \(i^{th}\) experimental unit
Therefore, for the data point circled in red:
we have:
\(x_i=75\) and \(y_i=208\)
And, using the unrounded version of the proposed line, the predicted weight of a randomly selected 75-inch tall student is:
\(\hat{y}_i=-266.534+6.13758(75)=193.8\)
pounds. Now, of course, the estimated line does not predict the weight of a 75-inch tall student perfectly. In this case, the prediction is 193.8 pounds, when the reality is 208 pounds. We have made an error in our prediction. That is, in using \(\hat{y}_i\) to predict the actual response \(y_i\) we make a prediction error (or a residual error) of size:
\(e_i=y_i-\hat{y}_i\)
Now, a line that fits the data well will be one for which the \(n\) prediction errors (one for each of the \(n\) data points — \(n=10\), in this case) are as small as possible in some overall sense. This idea is called the "least squares criterion." In short, the least squares criterion tells us that in order to find the equation of the best fitting line:
\(\hat{y}_i=a_1+bx_i\)
we need to choose the values \(a_1\) and \(b\) that minimize the sum of the squared prediction errors. That is, find \(a_1\) and \(b\) that minimize:
\(Q=\sum\limits_{i=1}^n (y_i-\hat{y}_i)^2=\sum\limits_{i=1}^n (y_i-(a_1+bx_i))^2\)
So, using the least squares criterion to determine which of the two lines:
- \(\text{weight} = −266.5 + 6.1 \times\text{height}\)
- \(\text{weight} = −331.2 + 7.1 \times \text{height}\)
is the best fitting line, we just need to determine \(Q\), the sum of the squared prediction errors for each of the two lines, and choose the line that has the smallest value of \(Q\). For the dashed line, that is, for the line:
\(\text{weight} = −331.2 + 7.1\times\text{height}\)
here's what the work would look like:
| i | \( x_i \) | \( y_i \) | \( \hat{y_i} \) | \( y_i -\hat{y_i} \) | \( (y_i - \hat{y_i})^2 \) |
|---|---|---|---|---|---|
| 1 | 64 | 121 | 123.2 | -2.2 | 4.84 |
| 2 | 73 | 181 | 187.1 | -6.1 | 37.21 |
| 3 | 71 | 156 | 172.9 | -16.9 | 285.61 |
| 4 | 69 | 162 | 158.7 | 3.3 | 10.89 |
| 5 | 66 | 142 | 137.4 | 4.6 | 21.16 |
| 6 | 69 | 157 | 158.7 | -1.7 | 2.89 |
| 7 | 75 | 208 | 201.3 | 6.7 | 44.89 |
| 8 | 71 | 169 | 172.9 | -3.9 | 15.21 |
| 9 | 63 | 127 | 116.1 | 10.9 | 118.81 |
| 10 | 72 | 165 | 180.0 | -15.0 |
225.00 |
| ------ | |||||
| 766.51 |
The first column labeled \(i\) just keeps track of the index of the data points, \(i=1, 2, \ldots, 10\). The columns labeled \(x_i\) and \(y_i\) contain the original data points. For example, the first student measured is 64 inches tall and weighs 121 pounds. The fourth column, labeled \(\hat{y}_i\), contains the predicted weight of each student. For example, the predicted weight of the first student, who is 64 inches tall, is:
\(\hat{y}_1=-331.2+7.1(64)=123.2\)
pounds. The fifth column contains the errors in using \(\hat{y}_i\) to predict \(y_i\). For the first student, the prediction error is:
\(e_1=121-123.3=-2.2\)
And, the last column contains the squared prediction errors. The squared prediction error for the first student is:
\(e^2_1=(-2.2)^2=4.84\)
By summing up the last column, that is, the column containing the squared prediction errors, we see that \(Q= 766.51\) for the dashed line. Now, for the solid line, that is, for the line:
\(\text{weight} = −266.5 + 6.1\times\text{height}\)
here's what the work would look like:
| i | \( x_i \) | \( y_i \) | \( \hat{y_i} \) | \( y_i -\hat{y_i} \) | \( (y_i - \hat{y_i})^2 \) |
|---|---|---|---|---|---|
| 1 | 64 | 121 | 126.271 | -5.3 | 28.9 |
| 2 | 73 | 181 | 181.509 | -0.5 | 0.25 |
| 3 | 71 | 156 | 169.234 | -13.2 | 174.24 |
| 4 | 69 | 162 | 156.959 | 5.0 | 25.00 |
| 5 | 66 | 142 | 138.546 | 3.5 | 12.25 |
| 6 | 69 | 157 | 156.959 | 0.0 | 0.00 |
| 7 | 75 | 208 | 193.784 | 14.2 | 201.64 |
| 8 | 71 | 169 | 169.234 | -0.2 | 0.04 |
| 9 | 63 | 127 | 120.133 | 6.9 | 47.61 |
| 10 | 72 | 165 | 175.371 | -10.4 |
108.16 |
| ------ | |||||
| 597.28 |
The calculations for each column are just as described previously. In this case, the sum of the last column, that is, the sum of the squared prediction errors for the solid line is \(Q= 597.28\). Choosing the equation that minimizes \(Q\), we can conclude that the solid line, that is:
\(\text{weight} = −266.5 + 6.1\times\text{height}\)
is the best fitting line.
In the preceding example, there's one major problem with concluding that the solid line is the best fitting line! We've only considered two possible candidates. There are, in fact, an infinite number of possible candidates for best fitting line. The approach we used above clearly won't work in practice. On the next page, we'll instead derive some formulas for the slope and the intercept for least squares regression line.
7.3 - Least Squares: The Theory
7.3 - Least Squares: The TheoryNow that we have the idea of least squares behind us, let's make the method more practical by finding a formula for the intercept \(a_1\) and slope \(b\). We learned that in order to find the least squares regression line, we need to minimize the sum of the squared prediction errors, that is:
\(Q=\sum\limits_{i=1}^n (y_i-\hat{y}_i)^2\)
We just need to replace that \(\hat{y}_i\) with the formula for the equation of a line:
\(\hat{y}_i=a_1+bx_i\)
to get:
\(Q=\sum\limits_{i=1}^n (y_i-\hat{y}_i)^2=\sum\limits_{i=1}^n (y_i-(a_1+bx_i))^2\)
We could go ahead and minimize \(Q\) as such, but our textbook authors have opted to use a different form of the equation for a line, namely:
\(\hat{y}_i=a+b(x_i-\bar{x})\)
Each form of the equation for a line has its advantages and disadvantages. Statistical software, such as Minitab, will typically calculate the least squares regression line using the form:
\(\hat{y}_i=a_1+bx_i\)
Clearly a plus if you can get some computer to do the dirty work for you. A (minor) disadvantage of using this form of the equation, though, is that the intercept \(a_1\) is the predicted value of the response \(y\) when the predictor \(x=0\), which is typically not very meaningful. For example, if \(x\) is a student's height (in inches) and \(y\) is a student's weight (in pounds), then the intercept \(a_1\) is the predicted weight of a student who is 0 inches tall..... errrr.... you get the idea. On the other hand, if we use the equation:
\(\hat{y}_i=a+b(x_i-\bar{x})\)
then the intercept \(a\) is the predicted value of the response \(y\) when the predictor \(x_i=\bar{x}\), that is, the average of the \(x\) values. For example, if \(x\) is a student's height (in inches) and \(y\) is a student's weight (in pounds), then the intercept \(a\) is the predicted weight of a student who is average in height. Much better, much more meaningful! The good news is that it is easy enough to get statistical software, such as Minitab, to calculate the least squares regression line in this form as well.
Okay, with that aside behind us, time to get to the punchline.
Least Squares Estimates
The least squares regression line is:
\(\hat{y}_i=a+b(x_i-\bar{x})\)
with least squares estimates:
\(a=\bar{y}\) and \(b=\dfrac{\sum\limits_{i=1}^n (x_i-\bar{x})(y_i-\bar{y})}{\sum\limits_{i=1}^n (x_i-\bar{x})^2}\)
Proof
In order to derive the formulas for the intercept \(a\) and slope \(b\), we need to minimize:
\(Q=\sum\limits_{i=1}^n (y_i-(a+b(x_i-\bar{x})))^2\)
Time to put on your calculus cap, as minimizing \(Q\) involves taking the derivative of \(Q\) with respect to \(a\) and \(b\), setting to 0, and then solving for \(a\) and \(b\). Let's do that. Starting with the derivative of \(Q\) with respect to \(a\), we get:
Now knowing that \(a\) is \(\bar{y}\), the average of the responses, let's replace \(a\) with \(\bar{y}\) in the formula for \(Q\):
\(Q=\sum\limits_{i=1}^n (y_i-(\bar{y}+b(x_i-\bar{x})))^2\)
and take the derivative of \(Q\) with respect to \(b\). Doing so, we get:
As was to be proved.
 By the way, you might want to note that the only assumption relied on for the above calculations is that the relationship between the response \(y\) and the predictor \(x\) is linear.
By the way, you might want to note that the only assumption relied on for the above calculations is that the relationship between the response \(y\) and the predictor \(x\) is linear.
Another thing you might note is that the formula for the slope \(b\) is just fine providing you have statistical software to make the calculations. But, what would you do if you were stranded on a desert island, and were in need of finding the least squares regression line for the relationship between the depth of the tide and the time of day? You'd probably appreciate having a simpler calculation formula! You might also appreciate understanding the relationship between the slope \(b\) and the sample correlation coefficient \(r\).
With that lame motivation behind us, let's derive alternative calculation formulas for the slope \(b\).
An alternative formula for the slope \(b\) of the least squares regression line:
\(\hat{y}_i=a+b(x_i-\bar{x})\)
is:
\(b=\dfrac{\sum\limits_{i=1}^n (x_i-\bar{x})y_i}{\sum\limits_{i=1}^n (x_i-\bar{x})^2}=\dfrac{\sum\limits_{i=1}^n x_iy_i-\left(\dfrac{1}{n}\right) \left(\sum\limits_{i=1}^n x_i\right) \left(\sum\limits_{i=1}^n y_i\right)}{\sum\limits_{i=1}^n x^2_i-\left(\dfrac{1}{n}\right) \left(\sum\limits_{i=1}^n x_i\right)^2}\)
Proof
The proof, which may or may not show up on a quiz or exam, is left for you as an exercise.
7.4 - The Model
7.4 - The ModelWhat do \(a\) and \(b\) estimate?
So far, we've formulated the idea, as well as the theory, behind least squares estimation. But, now we have a little problem. When we derived formulas for the least squares estimates of the intercept \(a\) and the slope \(b\), we never addressed for what parameters \(a\) and \(b\) serve as estimates. It is a crucial topic that deserves our attention. Let's investigate the answer by considering the (linear) relationship between high school grade point averages (GPAs) and scores on a college entrance exam, such as the ACT exam. Well, let's actually center the high school GPAs so that if \(x\) denotes the high school GPA, then \(x-\bar{x}\) is the centered high school GPA. Here's what a plot of \(x-\bar{x}\), the centered high school GPA, and \(y\), the college entrance test score might look like:
Well, okay, so that plot deserves some explanation:
So far, in summary, we are assuming two things. First, among the entire population of college students, there is some unknown linear relationship between \(\mu_y\), (or alternatively \(E(Y)\)), the average college entrance score, and \(x-\bar{x}\), centered high school GPA. That is:
\(\mu_Y=E(Y)=\alpha+\beta(x-\bar{x})\)
Second, individual students deviate from the mean college entrance test score of the population of students having the same centered high school GPA by some unknown amount \(\epsilon_i\). That is, if \(Y_i\) denotes the college entrance test score for student \(i\), then:
\(Y_i=\alpha+\beta(x-\bar{x})+\epsilon_i\)
Unfortunately, we don't have the luxury of collecting data on all of the college students in the population. So, we can never know the population intercept \(\alpha\) or the population slope \(\beta\). The best we can do is estimate \(\alpha\) and \(\beta\) by taking a random sample from the population of college students. Suppose we randomly select fifteen students from the population, in which three students have a centered high school GPA of −2, three students have a centered high school GPA of −1, and so on. We can use those fifteen data points to determine the best fitting (least squares) line:
\(\hat{y}_i=a+b(x_i-\bar{x})\)
Now, our least squares line isn't going to be perfect, but it should do a pretty good job of estimating the true unknown population line:
That's it in a nutshell. The intercept \(a\) and the slope \(b\) of the least squares regression line estimate, respectively, the intercept \(\alpha\) and the slope \(\beta\) of the unknown population line. The only assumption we make in doing so is that the relationship between the predictor \(x\) and the response \(y\) is linear.
Now, if we want to derive confidence intervals for \(\alpha\) and \(\beta\), as we are going to want to do on the next page, we are going to have to make a few more assumptions. That's where the simple linear regression model comes to the rescue.
The Simple Linear Regression Model
So that we can have properly drawn normal curves, let's borrow (steal?) an example from the textbook called Applied Linear Regression Models (4th edition, by Kutner, Nachtsheim, and Neter). Consider the relationship between \(x\), the number of bids contracting companies prepare, and \(y\), the number of hours it takes to prepare the bids:
A couple of things to note about this graph. Note that again, the mean number of hours, \(E(Y)\), is assumed to be linearly related to \(X\), the number of bids prepared. That's the first assumption. The textbook authors even go as far as to specify the values of typically unknown \(\alpha\) and \(\beta\). In this case, \(\alpha\) is 9.5 and \(\beta\) is 2.1.
Note that if \(X=45\) bids are prepared, then the expected number of hours it took to prepare the bids is:
\(\mu_Y=E(Y)=9.5+2.1(45)=104\)
In one case, it took a contracting company 108 hours to prepare 45 bids. In that case, the error \(\epsilon_i\) is 4. That is:
\(Y_i=108=E(Y)+\epsilon_i=104+4\)
The normal curves drawn for each value of \(X\) are meant to suggest that the error terms \(\epsilon_i\), and therefore the responses \(Y_i\), are normally distributed. That's a second assumption.
Did you also notice that the two normal curves in the plot are drawn to have the same shape? That suggests that each population (as defined by \(X\)) has a common variance. That's a third assumption. That is, the errors, \(\epsilon_i\), and therefore the responses \(Y_i\), have equal variances for all \(x\) values.
There's one more assumption that is made that is difficult to depict on a graph. That's the one that concerns the independence of the error terms. Let's summarize!
In short, the simple linear regression model states that the following four conditions must hold:
- The mean of the responses, \(E(Y_i)\), is a Linear function of the \(x_i\).
- The errors, \(\epsilon_i\), and hence the responses \(Y_i\), are Independent.
- The errors, \(\epsilon_i\), and hence the responses \(Y_i\), are Normally distributed.
- The errors, \(\epsilon_i\), and hence the responses \(Y_i\), have Equal variances (\(\sigma^2\)) for all \(x\) values.
Did you happen to notice that each of the four conditions is capitalized and emphasized in red? And, did you happen to notice that the capital letters spell L-I-N-E? Do you get it? We are investigating least squares regression lines, and the model effectively spells the word line! You might find this mnemonic an easy way to remember the four conditions.
Maximum Likelihood Estimators of \(\alpha\) and \(\beta\)
We know that \(a\) and \(b\):
\(\displaystyle{a=\bar{y} \text{ and } b=\dfrac{\sum\limits_{i=1}^n (x_i-\bar{x})(y_i-\bar{y})}{\sum\limits_{i=1}^n (x_i-\bar{x})^2}}\)
are ("least squares") estimators of \(\alpha\) and \(\beta\) that minimize the sum of the squared prediction errors. It turns out though that \(a\) and \(b\) are also maximum likelihood estimators of \(\alpha\) and \(\beta\) providing the four conditions of the simple linear regression model hold true.
If the four conditions of the simple linear regression model hold true, then:
\(\displaystyle{a=\bar{y}\text{ and }b=\dfrac{\sum\limits_{i=1}^n (x_i-\bar{x})(y_i-\bar{y})}{\sum\limits_{i=1}^n (x_i-\bar{x})^2}}\)
are maximum likelihood estimators of \(\alpha\) and \(\beta\).
Answer
The simple linear regression model, in short, states that the errors \(\epsilon_i\) are independent and normally distributed with mean 0 and variance \(\sigma^2\). That is:
\(\epsilon_i \sim N(0,\sigma^2)\)
The linearity condition:
\(Y_i=\alpha+\beta(x_i-\bar{x})+\epsilon_i\)
therefore implies that:
\(Y_i \sim N(\alpha+\beta(x_i-\bar{x}),\sigma^2)\)
Therefore, the likelihood function is:
\(\displaystyle{L_{Y_i}(\alpha,\beta,\sigma^2)=\prod\limits_{i=1}^n \dfrac{1}{\sqrt{2\pi}\sigma} \text{exp}\left[-\dfrac{(Y_i-\alpha-\beta(x_i-\bar{x}))^2}{2\sigma^2}\right]}\)
which can be rewritten as:
\(\displaystyle{L=(2\pi)^{-n/2}(\sigma^2)^{-n/2}\text{exp}\left[-\dfrac{1}{2\sigma^2} \sum\limits_{i=1}^n (Y_i-\alpha-\beta(x_i-\bar{x}))^2\right]}\)
Taking the log of both sides, we get:
\(\displaystyle{\text{log}L=-\dfrac{n}{2}\text{log}(2\pi)-\dfrac{n}{2}\text{log}(\sigma^2)-\dfrac{1}{2\sigma^2} \sum\limits_{i=1}^n (Y_i-\alpha-\beta(x_i-\bar{x}))^2} \)
Now, that negative sign in front of that summation on the right hand side:
\(\color{black}\text{log}L=-\dfrac{n}{2} \text{log} (2\pi)-\dfrac{n}{2}\text{log}\left(\sigma^{2}\right)\color{blue}\boxed{\color{black}-}\color{black}\dfrac{1}{2\sigma^{2}} \color{blue}\boxed{\color{black}\sum\limits_{i=1}^{n}\left(Y_{i}-\alpha-\beta\left(x_{i}-\bar{x}\right)\right)^{2}}\)
tells us that the only way we can maximize \(\text{log}L(\alpha,\beta,\sigma^2)\) with respect to \(\alpha\) and \(\beta\) is if we minimize:
\(\displaystyle{\sum\limits_{i=1}^n (Y_i-\alpha-\beta(x_i-\bar{x}))^2}\)
with respect to \(\alpha\) and \(\beta\). Hey, but that's just the least squares criterion! Therefore, the ML estimators of \(\alpha\) and \(\beta\) must be the same as the least squares estimators \(\alpha\) and \(\beta\). That is:
\(\displaystyle{a=\bar{y}\text{ and }b=\dfrac{\sum\limits_{i=1}^n (x_i-\bar{x})(y_i-\bar{y})}{\sum\limits_{i=1}^n (x_i-\bar{x})^2}}\)
are maximum likelihood estimators of \(\alpha\) and \(\beta\) under the assumption that the error terms are independent, normally distributed with mean 0 and variance \(\sigma^2\). As was to be proved!
What about the (Unknown) Variance \(\sigma^2\)?
In short, the variance \(\sigma^2\) quantifies how much the responses (\(y\)) vary around the (unknown) mean regression line \(E(Y)\). Now, why should we care about the magnitude of the variance \(\sigma^2\)? The following example might help to illuminate the answer to that question.
Example 7-2

We know that there is a perfect relationship between degrees Celsius (C) and degrees Fahrenheit (F), namely:
\(F=\dfrac{9}{5}C+32\)
Suppose we are unfortunate, however, and therefore don't know the relationship. We might attempt to learn about the relationship by collecting some temperature data and calculating a least squares regression line. When all is said and done, which brand of thermometers do you think would yield more precise future predictions of the temperature in Fahrenheit? The one whose data are plotted on the left? Or the one whose data are plotted on the right?
|
|
|
Answer
As you can see, for the plot on the left, the Fahrenheit temperatures do not vary or "bounce" much around the estimated regression line. For the plot on the right, on the other hand, the Fahrenheit temperatures do vary or "bounce" quite a bit around the estimated regression line. It seems reasonable to conclude then that the brand of thermometers on the left will yield more precise future predictions of the temperature in Fahrenheit.
Now, the variance \(\sigma^2\) is, of course, an unknown population parameter. The only way we can attempt to quantify the variance is to estimate it. In the case in which we had one population, say the (normal) population of IQ scores:
we would estimate the population variance \(\sigma^2\) using the sample variance:
\(s^2=\dfrac{\sum\limits_{i=1}^n (Y_i-\bar{Y})^2}{n-1}\)
We have learned that \(s^2\) is an unbiased estimator of \(\sigma^2\), the variance of the one population. But what if we no longer have just one population, but instead have many populations? In our bids and hours example, there is a population for every value of \(x\):
In this case, we have to estimate \(\sigma^2\), the (common) variance of the many populations. There are two possibilities − one is a biased estimator, and one is an unbiased estimator.
The maximum likelihood estimator of \(\sigma^2\) is:
\(\hat{\sigma}^2=\dfrac{\sum\limits_{i=1}^n (Y_i-\hat{Y}_i)^2}{n}\)
(It is a biased estimator of \(\sigma^2\), the common variance of the many populations.
Answer
We have previously shown that the log of the likelihood function is:
\(\text{log}L=-\dfrac{n}{2}\text{log}(2\pi)-\dfrac{n}{2}\text{log}(\sigma^2)-\dfrac{1}{2\sigma^2} \sum\limits_{i=1}^n (Y_i-\alpha-\beta(x_i-\bar{x}))^2 \)
To maximize the log likelihood, we have to take the partial derivative of the log likelihood with respect to \(\sigma^2\). Doing so, we get:
\(\dfrac{\partial L_{Y_i}(\alpha,\beta,\sigma^2)}{\partial \sigma^2}=-\dfrac{n}{2\sigma^2}-\dfrac{1}{2}\sum (Y_i-\alpha-\beta(x_i-\bar{x}))^2 \cdot \left(- \dfrac{1}{(\sigma^2)^2}\right)\)
Setting the derivative equal to 0, and multiplying through by \(2\sigma^4\):
\(\frac{\partial L_{Y_{i}}\left(\alpha, \beta, \sigma^{2}\right)}{\partial \sigma^{2}}=\left[-\frac{n}{2 \sigma^{2}}-\frac{1}{2} \sum\left(Y_{i}-\alpha-\beta\left(x_{i}-\bar{x}\right)\right)^{2} \cdot-\frac{1}{\left(\sigma^{2}\right)^{2}} \stackrel{\operatorname{SET}}{\equiv} 0\right] 2\left(\sigma^{2}\right)^{2}\)
we get:
\(-n\sigma^2+\sum (Y_i-\alpha-\beta(x_i-\bar{x}))^2 =0\)
And, solving for and putting a hat on \(\sigma^2\), as well as replacing \(\alpha\) and \(\beta\) with their ML estimators, we get:
\(\hat{\sigma}^2=\dfrac{\sum (Y_i-\alpha-\beta(x_i-\bar{x}))^2 }{n}=\dfrac{\sum(Y_i-\hat{Y}_i)^2}{n}\)
As was to be proved!
- Mean Square Error
-
The mean square error, on the other hand:
\(MSE=\dfrac{\sum\limits_{i=1}^n(Y_i-\hat{Y}_i)^2}{n-2}\)
is an unbiased estimator of \(\sigma^2\), the common variance of the many populations.
We'll need to use these estimators of \(\sigma^2\) when we derive confidence intervals for \(\alpha\) and \(\beta\) on the next page.
7.5 - Confidence Intervals for Regression Parameters
7.5 - Confidence Intervals for Regression ParametersBefore we can derive confidence intervals for \(\alpha\) and \(\beta\), we first need to derive the probability distributions of \(a, b\) and \(\hat{\sigma}^2\). In the process of doing so, let's adopt the more traditional estimator notation, and the one our textbook follows, of putting a hat on greek letters. That is, here we'll use:
\(a=\hat{\alpha}\) and \(b=\hat{\beta}\)
Theorem
Under the assumptions of the simple linear regression model:
\(\hat{\alpha}\sim N\left(\alpha,\dfrac{\sigma^2}{n}\right)\)
Proof
Recall that the ML (and least squares!) estimator of \(\alpha\) is:
\(a=\hat{\alpha}=\bar{Y}\)
where the responses \(Y_i\) are independent and normally distributed. More specifically:
\(Y_i \sim N(\alpha+\beta(x_i-\bar{x}),\sigma^2)\)
The expected value of \(\hat{\alpha}\) is \(\alpha\), as shown here:
\(E(\hat{\alpha})=E(\bar{Y})=\frac{1}{n}\sum E(Y_i)=\frac{1}{n}\sum E(\alpha+\beta(x_i-\bar{x})=\frac{1}{n}\left[n\alpha+\beta \sum (x_i-\bar{x})\right]=\frac{1}{n}(n\alpha)=\alpha\)
because \(\sum (x_i-\bar{x})=0\).
The variance of \(\hat{\alpha}\) follow directly from what we know about the variance of a sample mean, namely:
\(Var(\hat{\alpha})=Var(\bar{Y})=\dfrac{\sigma^2}{n}\)
Therefore, since a linear combination of normal random variables is also normally distributed, we have:
\(\hat{\alpha} \sim N\left(\alpha,\dfrac{\sigma^2}{n}\right)\)
as was to be proved!
Theorem
Under the assumptions of the simple linear regression model:
\(\hat{\beta}\sim N\left(\beta,\dfrac{\sigma^2}{\sum_{i=1}^n (x_i-\bar{x})^2}\right)\)
Proof
Recalling one of the shortcut formulas for the ML (and least squares!) estimator of \(\beta \colon\)
\(b=\hat{\beta}=\dfrac{\sum_{i=1}^n (x_i-\bar{x})Y_i}{\sum_{i=1}^n (x_i-\bar{x})^2}\)
we see that the ML estimator is a linear combination of independent normal random variables \(Y_i\) with:
\(Y_i \sim N(\alpha+\beta(x_i-\bar{x}),\sigma^2)\)
The expected value of \(\hat{\beta}\) is \(\beta\), as shown here:
\(E(\hat{\beta})=\frac{1}{\sum (x_i-\bar{x})^2}\sum E\left[(x_i-\bar{x})Y_i\right]=\frac{1}{\sum (x_i-\bar{x})^2}\sum (x_i-\bar{x})(\alpha +\beta(x_i-\bar{x}) =\frac{1}{\sum (x_i-\bar{x})^2}\left[ \alpha\sum (x_i-\bar{x}) +\beta \sum (x_i-\bar{x})^2 \right] \\=\beta \)
because \(\sum (x_i-\bar{x})=0\).
And, the variance of \(\hat{\beta}\) is:
\(\text{Var}(\hat{\beta})=\left[\frac{1}{\sum (x_i-\bar{x})^2}\right]^2\sum (x_i-\bar{x})^2(\text{Var}(Y_i))=\frac{\sigma^2}{\sum (x_i-\bar{x})^2}\)
Therefore, since a linear combination of normal random variables is also normally distributed, we have:
\(\hat{\beta}\sim N\left(\beta,\dfrac{\sigma^2}{\sum_{i=1}^n (x_i-\bar{x})^2}\right)\)
as was to be proved!
Theorem
Under the assumptions of the simple linear regression model:
\(\dfrac{n\hat{\sigma}^2}{\sigma^2}\sim \chi^2_{(n-2)}\)
and \(a=\hat{\alpha}\), \(b=\hat{\beta}\), and \(\hat{\sigma}^2\) are mutually independent.
Argument
First, note that the heading here says Argument, not Proof. That's because we are going to be doing some hand-waving and pointing to another reference, as the proof is beyond the scope of this course. That said, let's start our hand-waving. For homework, you are asked to show that:
\(\sum\limits_{i=1}^n (Y_i-\alpha-\beta(x_i-\bar{x}))^2=n(\hat{\alpha}-\alpha)^2+(\hat{\beta}-\beta)^2\sum\limits_{i=1}^n (x_i-\bar{x})^2+\sum\limits_{i=1}^n (Y_i-\hat{Y})^2\)
Now, if we divide through both sides of the equation by the population variance \(\sigma^2\), we get:
\(\dfrac{\sum_{i=1}^n (Y_i-\alpha-\beta(x_i-\bar{x}))^2 }{\sigma^2}=\dfrac{n(\hat{\alpha}-\alpha)^2}{\sigma^2}+\dfrac{(\hat{\beta}-\beta)^2\sum\limits_{i=1}^n (x_i-\bar{x})^2}{\sigma^2}+\dfrac{\sum (Y_i-\hat{Y})^2}{\sigma^2}\)
Rewriting a few of those terms just a bit, we get:
\(\dfrac{\sum_{i=1}^n (Y_i-\alpha-\beta(x_i-\bar{x}))^2 }{\sigma^2}=\dfrac{(\hat{\alpha}-\alpha)^2}{\sigma^2/n}+\dfrac{(\hat{\beta}-\beta)^2}{\sigma^2/\sum\limits_{i=1}^n (x_i-\bar{x})^2}+\dfrac{n\hat{\sigma}^2}{\sigma^2}\)
Now, the terms are written so that we should be able to readily identify the distributions of each of the terms. The distributions are:
${\displaystyle\underbrace{\color{black}\frac{\sum\left(Y_{i}-\alpha-\beta\left(x_{i}-\bar{x}\right)\right)^{2}}{\sigma^2}}_{\underset{\text{}}{{\color{blue}x^2_{(n)}}}}=
\underbrace{\color{black}\frac{(\hat{\alpha}-\alpha)^{2}}{\sigma^{2} / n}}_{\underset{\text{}}{{\color{blue}x^2_{(1)}}}}+
\underbrace{\color{black}\frac{(\hat{\beta}-\beta)^{2}}{\sigma^{2} / \sum\left(x_{i}-\bar{x}\right)^{2}}}_{\underset{\text{}}{{\color{blue}x^2_{(1)}}}}+
\underbrace{\color{black}\frac{n \hat{\sigma}^{2}}{\sigma^{2}}}_{\underset{\text{}}{\color{red}\text{?}}}}$
Now, it might seem reasonable that the last term is a chi-square random variable with \(n-2\) degrees of freedom. That is .... hand-waving! ... indeed the case. That is:
\(\dfrac{n\hat{\sigma}^2}{\sigma^2} \sim \chi^2_{(n-2)}\)
and furthermore (more hand-waving!), \(a=\hat{\alpha}\), \(b=\hat{\beta}\), and \(\hat{\sigma}^2\) are mutually independent. (For a proof, you can refer to any number of mathematical statistics textbooks, but for a proof presented by one of the authors of our textbook, see Hogg, McKean, and Craig, Introduction to Mathematical Statistics, 6th ed.)
With the distributional results behind us, we can now derive \((1-\alpha)100\%\) confidence intervals for \(\alpha\) and \(\beta\)!
Theorem
Under the assumptions of the simple linear regression model, a \((1-\alpha)100\%\) confidence interval for the slope parameter \(\beta\) is:
\(b \pm t_{\alpha/2,n-2}\times \left(\dfrac{\sqrt{n}\hat{\sigma}}{\sqrt{n-2} \sqrt{\sum (x_i-\bar{x})^2}}\right)\)
or equivalently:
\(\hat{\beta} \pm t_{\alpha/2,n-2}\times \sqrt{\dfrac{MSE}{\sum (x_i-\bar{x})^2}}\)
Proof
Recall the definition of a \(T\) random variable. That is, recall that if:
- \(Z\) is a standard normal ( \(N(0,1)\)) random variable
- \(U\) is a chi-square random variable with \(r\) degrees of freedom
- \(Z\) and \(U\) are independent, then:
\(T=\dfrac{Z}{\sqrt{U/r}}\)
follows a \(T\) distribution with \(r\) degrees of freedom. Now, our work above tells us that:
\(\dfrac{\hat{\beta}-\beta}{\sigma/\sqrt{\sum (x_i-\bar{x})^2}} \sim N(0,1) \) and \(\dfrac{n\hat{\sigma}^2}{\sigma^2} \sim \chi^2_{(n-2)}\) are independent
Therefore, we have that:
\(T=\dfrac{\dfrac{\hat{\beta}-\beta}{\sigma/\sqrt{\sum (x_i-\bar{x})^2}}}{\sqrt{\dfrac{n\hat{\sigma}^2}{\sigma^2}/(n-2)}}=\dfrac{\hat{\beta}-\beta}{\sqrt{\dfrac{n\hat{\sigma}^2}{n-2}/\sum (x_i-\bar{x})^2}}=\dfrac{\hat{\beta}-\beta}{\sqrt{MSE/\sum (x_i-\bar{x})^2}} \sim t_{n-2}\)
follows a \(T\) distribution with \(n-2\) degrees of freedom. Now, deriving a confidence interval for \(\beta\) reduces to the usual manipulation of the inside of a probability statement:
\(P\left(-t_{\alpha/2} \leq \dfrac{\hat{\beta}-\beta}{\sqrt{MSE/\sum (x_i-\bar{x})^2}} \leq t_{\alpha/2}\right)=1-\alpha\)
leaving us with:
\(\hat{\beta} \pm t_{\alpha/2,n-2}\times \sqrt{\dfrac{MSE}{\sum (x_i-\bar{x})^2}}\)
as was to be proved!
Now, for the confidence interval for the intercept parameter \(\alpha\).
Theorem
Under the assumptions of the simple linear regression model, a \((1-\alpha)100\%\) confidence interval for the intercept parameter \(\alpha\) is:
\(a \pm t_{\alpha/2,n-2}\times \left(\sqrt{\dfrac{\hat{\sigma}^2}{n-2}}\right)\)
or equivalently:
\(a \pm t_{\alpha/2,n-2}\times \left(\sqrt{\dfrac{MSE}{n}}\right)\)
Proof
The proof, which again may or may not appear on a future assessment, is left for you for homework.
Example 7-3

The following table shows \(x\), the catches of Peruvian anchovies (in millions of metric tons) and \(y\), the prices of fish meal (in current dollars per ton) for 14 consecutive years. (Data from Bardach, JE and Santerre, RM, Climate and the Fish in the Sea, Bioscience 31(3), 1981).
| Row | Price | Catch |
|---|---|---|
| 1 | 190 | 7.23 |
| 2 | 160 | 8.53 |
| 3 | 134 | 9.82 |
| 4 | 129 | 10.26 |
| 5 | 172 | 8.96 |
| 6 | 197 | 12.27 |
| 7 | 167 | 10.28 |
| 8 | 239 | 4.45 |
| 9 | 542 | 1.87 |
| 10 | 372 | 4.00 |
| 11 | 245 | 3.30 |
| 12 | 376 | 4.30 |
| 13 | 454 | 0.80 |
| 14 | 410 | 0.50 |
Find a 95% confidence interval for the slope parameter \(\beta\).
Answer
The following portion of output was obtained using Minitab's regression analysis package, with the parts useful to us here circled:
| The regression equation is Price = 452 - 29.4 Catch |
||||
|---|---|---|---|---|
| Predictor | Coef | SE Coef | T | P |
| Constant | 452.12 | 36.82 | 12.28 | 0.000 |
| Catch | -29.402 | 5.091 | -5.78 | 0.000 |
|
|
\(\color{blue}\hat{\beta}\uparrow\) |
|||
| S = 71.6866 | R-Sq = 73.5% | R-Sq(adj) = 71.3% | ||
Analysis of Variance
| Source | DF | SS | MS | F | P |
|---|---|---|---|---|---|
| Regression | 1 | 171414 | 171414 | 33.36 | 0.000 |
| Residual Error | 12 | 61668 | 5139 | 0.000 | |
|
Total |
13 | 233081 |
\(\color{blue}MSE\uparrow\) |
Minitab's basic descriptive analysis can also calculate the standard deviation of the \(x\)-values, 3.91, for us. Therefore, the formula for the sample variance tells us that:
\(\sum\limits_{i=1}^n (x_i-\bar{x})^2=(n-1)s^2=(13)(3.91)^2=198.7453\)
Putting the parts together, along with the fact that \t_{0.025, 12}=2.179\), we get:
\(-29.402 \pm 2.179 \sqrt{\dfrac{5139}{198.7453}}\)
which simplifies to:
\(-29.402 \pm 11.08\)
That is, we can be 95% confident that the slope parameter falls between −40.482 and −18.322. That is, we can be 95% confident that the average price of fish meal decreases between 18.322 and 40.482 dollars per ton for every one unit (one million metric ton) increase in the Peruvian anchovy catch.
Find a 95% confidence interval for the intercept parameter \(\alpha\).
Answer
We can use Minitab (or our calculator) to determine that the mean of the 14 responses is:
\(\dfrac{190+160+\cdots +410}{14}=270.5\)
Using that, as well as the MSE = 5139 obtained from the output above, along with the fact that \(t_{0.025,12} = 2.179\), we get:
\(270.5 \pm 2.179 \sqrt{\dfrac{5139}{14}}\)
which simplifies to:
\(270.5 \pm 41.75\)
That is, we can be 95% confident that the intercept parameter falls between 228.75 and 312.25 dollars per ton.
7.6 - Using Minitab to Lighten the Workload
7.6 - Using Minitab to Lighten the WorkloadLeast Squares Regression Line
There are (at least) two ways that we can ask Minitab to calculate a least squares regression line for us. Let's use the height and weight example from the last page to illustrate. In either case, we first need to enter the data into two columns, as follows:
Now, the first method involves asking Minitab to create a fitted line plot. You can find the fitted line plot under the Stat menu. Select Stat >> Regression >> Fitted Line Plot..., as illustrated here:
In the pop-up window that appears, tell Minitab which variable is the Response (Y) and which variable is the Predictor (X). In our case, we select weight as the response, and height as the predictor:
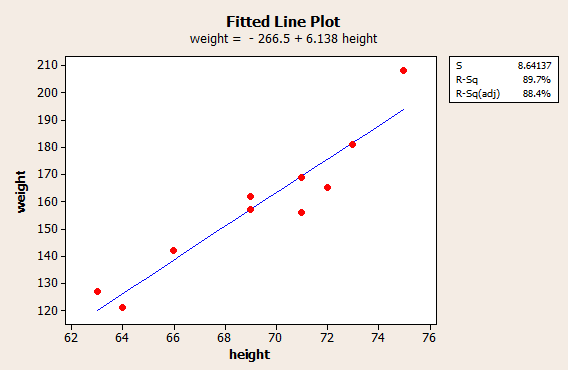
Then, select OK. A new graphics window should appear containing not only an equation, but also a graph, of the estimated regression line:
The second method involves asking Minitab to perform a regression analysis. You can find regression, again, under the Stat menu. Select Stat >>Regression >> Regression..., as illustrated here:
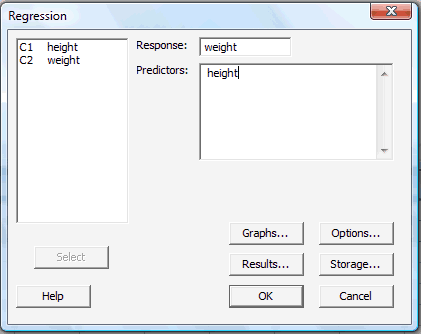
In the pop-up window that appears, again tell Minitab which variable is the Response (Y) and which variable is the Predictor (X). In our case, we again select weight as the response, and height as the predictor:
Then, select OK. The resulting analysis:
| The regression equation is weight = - 267 - 6.14 height |
||||
|---|---|---|---|---|
| Predictor | Coef | SE Coef | T | P |
| Constant | -266.53 | 51.03 | -5.22 | 0.001 |
| height | 6.1376 | 0.7353 | 8.35 | 0.000 |
|
|
|
|||
| S = 8.641 | R-Sq = 89.7% | R-Sq(adj) = 88.4% | ||
should appear in the Session window. You may have to page up in the Session window to see all of the analysis. (The above output just shows part of the analysis, with the portion pertaining to the estimated regression line highlighted in bold and blue.)
Now, as mentioned earlier, Minitab, by default, estimates the regression equation of the form:
\(\hat{y}_i=a_1+bx_i\)
It's easy enough to get Minitab to estimate the regression equation of the form:
\(\hat{y}_i=a+b(x_i-\bar{x})\)
We can first ask Minitab to calculate \(\bar{x}\) the mean height of the 10 students. The easiest way is to ask Minitab to calculate column statistics on the data in the height column. Select Calc >> Column Statistics...:
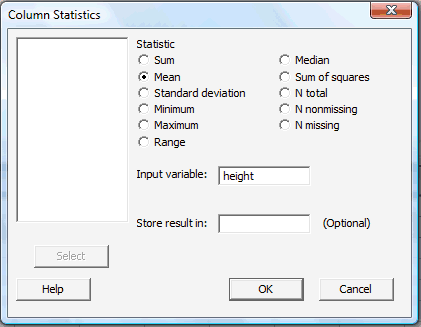
Then, select Mean, tell Minitab that the Input variable is height:
When you select OK, Minitab will display the results in the Session window:

Now, using the fact that the mean height is 69.3 inches, we need to calculate a new variable called, say, height* that equals height minus 69.3. We can do that using Minitab's calculator. First, label an empty column, C3, say height*:
Then, under Calc, select Calculator...:
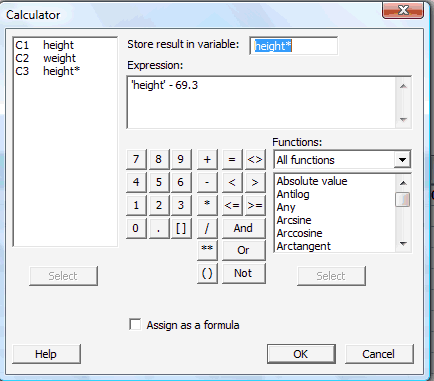
Use the calculator that appears in the pop-up window to tell Minitab to make the desired calculation:
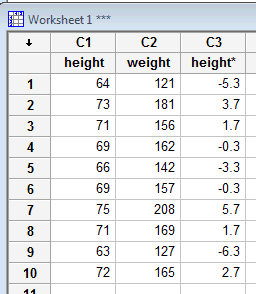
When you select OK, Minitab will enter the newly calculated data in the column labeled height*:
Now, it's just a matter of asking Minitab to performing another regression analysis... this time with the response as weight and the predictor as height*. Upon doing so, the resulting fitted line plot looks like this:
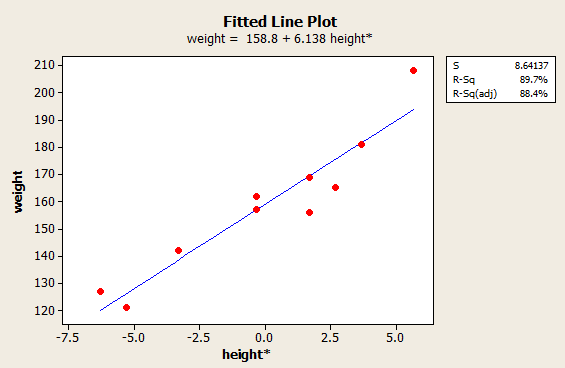
and the resulting regression analysis looks like this (with the portion pertaining to the estimated regression line highlighted in bold and blue):
| The regression equation is weight = 159 + 6.14 height* |
||||
|---|---|---|---|---|
| Predictor | Coef | SE Coef | T | P |
| Constant | 158.800 | 2.733 | 58.11 | 0.000 |
| height* | 6.1376 | 0.7353 | 8.35 | 0.000 |
|
|
|
|||
| S = 8.641 | R-Sq = 89.7% | R-Sq(adj) = 88.4% | ||
Estimating the Variance \(\sigma^2\)
You might not have noticed it, but we've already asked Minitab to estimate the common variance \(\sigma^2\)... or perhaps it's more accurate to say that Minitab calculates an estimate of the variance \(\sigma^2\), by default, every time it creates a fitted line plot or conducts a regression analysis. Here's where you'll find an estimate of the variance in the fitted line plot of our weight and height* data:
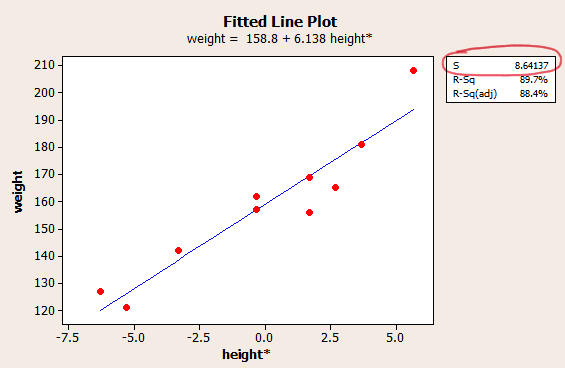
Well, okay, it would have been more accurate to say an estimate of the standard deviation \(\sigma\). We can simply square the estimate \(S\) (8.64137) to get the estimate \(S^2\) (74.67) of the variance \(\sigma^2\).
And, here's where you'll find an estimate of the variance in the fitted line plot of our weight and height data:
| The regression equation is weight = - 267 - 6.14 height |
||||
|---|---|---|---|---|
| Predictor | Coef | SE Coef | T | P |
| Constant | -266.53 | 51.03 | -5.22 | 0.001 |
| height | 6.1376 | 0.7353 | 8.35 | 0.000 |
|
|
|
|||
| S = 8.641 | R-Sq = 89.7% | R-Sq(adj) = 88.4% | ||
| Analysis of Variance | |||||
|---|---|---|---|---|---|
| Source | DF | SS | MS | F | P |
| Regression | 1 | 5202.2 | 5202.2 | 69.67 | 0.000 |
| Residual Error | 8 | 597.4 | 74.4 | 0.000 | |
|
Total |
9 | 5799.6 |
|
||
Here, we can see where Minitab displays not only \(S\), the estimate of the population standard deviation \(\sigma\), but also MSE (the Mean Square Error), the estimate of the population variance \(\sigma^2\). By the way, we shouldn't be surprised that the estimate of the variance is the same regardless of whether we use height or height* as the predictor. Right?