24.2 - Factorization Theorem

Answer

Because \(X_1, X_2, \ldots, X_n\) is a random sample, the joint probability mass function of \(X_1, X_2, \ldots, X_n\) is, by independence:

\(f(x_1, x_2, ... , x_n;\lambda) = f(x_1;\lambda) \times f(x_2;\lambda) \times ... \times f(x_n;\lambda)\)

Inserting what we know to be the probability mass function of a Poisson random variable with parameter \(\lambda\), the joint p.m.f. is therefore:

\(f(x_1, x_2, ... , x_n;\lambda) = \dfrac{e^{-\lambda}\lambda^{x_1}}{x_1!} \times\dfrac{e^{-\lambda}\lambda^{x_2}}{x_2!} \times ... \times \dfrac{e^{-\lambda}\lambda^{x_n}}{x_n!}\)

Now, simplifying, by adding up all \(n\) of the \(\lambda\)s in the exponents, as well as all \(n\) of the \(x_i\)'s in the exponents, we get:

\(f(x_1, x_2, ... , x_n;\lambda) = \left(e^{-n\lambda}\lambda^{\Sigma x_i} \right) \times \left( \dfrac{1}{x_1! x_2! ... x_n!} \right)\)

Hey, look at that! We just factored the joint p.m.f. into two functions, one (\(\phi\)) being only a function of the statistic \(Y=\sum_{i=1}^{n}X_i\) and the other (h) not depending on the parameter \(\lambda\):

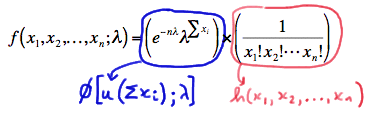
Therefore, the Factorization Theorem tells us that \(Y=\sum_{i=1}^{n}X_i\) is a sufficient statistic for \(\lambda\). But, wait a second! We can also write the joint p.m.f. as:

\(f(x_1, x_2, ... , x_n;\lambda) = \left(e^{-n\lambda}\lambda^{n\bar{x}} \right) \times \left( \dfrac{1}{x_1! x_2! ... x_n!} \right)\)

Therefore, the Factorization Theorem tells us that \(Y = \bar{X}\) is also a sufficient statistic for \(\lambda\)!

If you think about it, it makes sense that \(Y = \bar{X}\) and \(Y=\sum_{i=1}^{n}X_i\) are both sufficient statistics, because if we know \(Y = \bar{X}\), we can easily find \(Y=\sum_{i=1}^{n}X_i\). And, if we know \(Y=\sum_{i=1}^{n}X_i\), we can easily find \(Y = \bar{X}\).

Answer

Because \(X_1, X_2, \ldots, X_n\) is a random sample, the joint probability density function of \(X_1, X_2, \ldots, X_n\) is, by independence:

\(f(x_1, x_2, ... , x_n;\mu) = f(x_1;\mu) \times f(x_2;\mu) \times ... \times f(x_n;\mu)\)

Inserting what we know to be the probability density function of a normal random variable with mean \(\mu\) and variance 1, the joint p.d.f. is:

\(f(x_1, x_2, ... , x_n;\mu) = \dfrac{1}{(2\pi)^{1/2}} exp \left[ -\dfrac{1}{2}(x_1 - \mu)^2 \right] \times \dfrac{1}{(2\pi)^{1/2}} exp \left[ -\dfrac{1}{2}(x_2 - \mu)^2 \right] \times ... \times \dfrac{1}{(2\pi)^{1/2}} exp \left[ -\dfrac{1}{2}(x_n - \mu)^2 \right] \)

Collecting like terms, we get:

\(f(x_1, x_2, ... , x_n;\mu) = \dfrac{1}{(2\pi)^{n/2}} exp \left[ -\dfrac{1}{2}\sum_{i=1}^{n}(x_i - \mu)^2 \right]\)

A trick to making the factoring of the joint p.d.f. an easier task is to add 0 to the quantity in parentheses in the summation. That is:

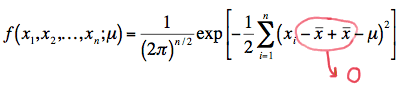
Now, squaring the quantity in parentheses, we get:

\(f(x_1, x_2, ... , x_n;\mu) = \dfrac{1}{(2\pi)^{n/2}} exp \left[ -\dfrac{1}{2}\sum_{i=1}^{n}\left[ (x_i - \bar{x})^2 +2(x_i - \bar{x}) (\bar{x}-\mu)+ (\bar{x}-\mu)^2\right] \right]\)

And then distributing the summation, we get:

\(f(x_1, x_2, ... , x_n;\mu) = \dfrac{1}{(2\pi)^{n/2}} exp \left[ -\dfrac{1}{2}\sum_{i=1}^{n} (x_i - \bar{x})^2 - (\bar{x}-\mu) \sum_{i=1}^{n}(x_i - \bar{x}) -\dfrac{1}{2}\sum_{i=1}^{n}(\bar{x}-\mu)^2\right] \)

But, the middle term in the exponent is 0, and the last term, because it doesn't depend on the index \(i\), can be added up \(n\) times:

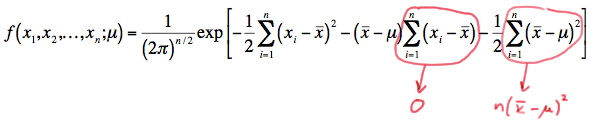
So, simplifying, we get:

\(f(x_1, x_2, ... , x_n;\mu) = \left\{ exp \left[ -\dfrac{n}{2} (\bar{x}-\mu)^2 \right] \right\} \times \left\{ \dfrac{1}{(2\pi)^{n/2}} exp \left[ -\dfrac{1}{2}\sum_{i=1}^{n} (x_i - \bar{x})^2 \right] \right\} \)

In summary, we have factored the joint p.d.f. into two functions, one (\(\phi\)) being only a function of the statistic \(Y = \bar{X}\) and the other (h) not depending on the parameter \(\mu\):

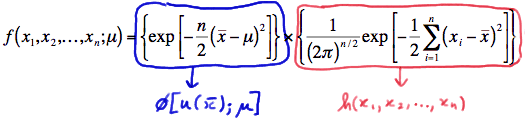
Therefore, the Factorization Theorem tells us that \(Y = \bar{X}\) is a sufficient statistic for \(\mu\). Now, \(Y = \bar{X}^3\) is also sufficient for \(\mu\), because if we are given the value of \( \bar{X}^3\), we can easily get the value of \(\bar{X}\) through the one-to-one function \(w=y^{1/3}\). That is:

\( W=(\bar{X}^3)^{1/3}=\bar{X} \)

On the other hand, \(Y = \bar{X}^2\) is not a sufficient statistic for \(\mu\), because it is not a one-to-one function. That is, if we are given the value of \(\bar{X}^2\), using the inverse function:

\(w=y^{1/2}\)

we get two possible values, namely:

\(-\bar{X}\) and \(+\bar{X}\)

Answer

Because \(X_1, X_2, \ldots, X_n\) is a random sample, the joint probability density function of \(X_1, X_2, \ldots, X_n\) is, by independence:

\(f(x_1, x_2, ... , x_n;\theta) = f(x_1;\theta) \times f(x_2;\theta) \times ... \times f(x_n;\theta)\)

Inserting what we know to be the probability density function of an exponential random variable with parameter \(\theta\), the joint p.d.f. is:

\(f(x_1, x_2, ... , x_n;\theta) =\dfrac{1}{\theta}exp\left( \dfrac{-x_1}{\theta}\right) \times \dfrac{1}{\theta}exp\left( \dfrac{-x_2}{\theta}\right) \times ... \times \dfrac{1}{\theta}exp\left( \dfrac{-x_n}{\theta} \right) \)

Now, simplifying, by adding up all \(n\) of the \(\theta\)s and the \(n\) \(x_i\)'s in the exponents, we get:

\(f(x_1, x_2, ... , x_n;\theta) =\dfrac{1}{\theta^n}exp\left( - \dfrac{1}{\theta} \sum_{i=1}^{n} x_i\right) \)

We have again factored the joint p.d.f. into two functions, one (\(\phi\)) being only a function of the statistic \(Y=\sum_{i=1}^{n}X_i\) and the other (h) not depending on the parameter \(\theta\):

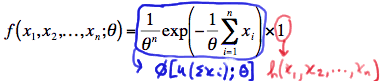
Therefore, the Factorization Theorem tells us that \(Y=\sum_{i=1}^{n}X_i\) is a sufficient statistic for \(\theta\). And, since \(Y = \bar{X}\) is a one-to-one function of \(Y=\sum_{i=1}^{n}X_i\), it implies that \(Y = \bar{X}\) is also a sufficient statistic for \(\theta\).