26.2 - Uniformly Most Powerful Tests
26.2 - Uniformly Most Powerful TestsThe Neyman Pearson Lemma is all well and good for deriving the best hypothesis tests for testing a simple null hypothesis against a simple alternative hypothesis, but the reality is that we typically are interested in testing a simple null hypothesis, such as \(H_0 \colon \mu = 10\) against a composite alternative hypothesis, such as \(H_A \colon \mu > 10\). The good news is that we can extend the Neyman Pearson Lemma to account for composite alternative hypotheses, providing we take into account each simple alternative specified in H_A. Doing so creates what is called a uniformly most powerful (or UMP) test.
- Uniformly Most Powerful (UMP) test
-
A test defined by a critical region C of size \(\alpha\) is a uniformly most powerful (UMP) test if it is a most powerful test against each simple alternative in the alternative hypothesis \(H_A\). The critical region C is called a uniformly most powerful critical region of size \(\alpha\).
Let's demonstrate by returning to the normal example from the previous page, but this time specifying a composite alternative hypothesis.
Example 26-6

Suppose \(X_1, X_2, \colon, X_n\) is a random sample from a normal population with mean \(\mu\) and variance 16. Find the test with the best critical region, that is, find the uniformly most powerful test, with a sample size of \(n = 16\) and a significance level \(\alpha\) = 0.05 to test the simple null hypothesis \(H_0: \mu = 10\) against the composite alternative hypothesis \(H_A: \mu > 10\).
Answer
For each simple alternative in \(H_A , \mu = \mu_a\), say, the ratio of the likelihood functions is:
\( \dfrac{L(10)}{L(\mu_\alpha)}= \dfrac{(32\pi)^{-16/2} exp \left[ -(1/32)\sum_{i=1}^{16}(x_i -10)^2 \right]}{(32\pi)^{-16/2} exp \left[ -(1/32)\sum_{i=1}^{16}(x_i -\mu_\alpha)^2 \right]} \le k \)
Simplifying, we get:
\(exp \left[ - \left(\dfrac{1}{32} \right) \left(\sum_{i=1}^{16}(x_i -10)^2 - \sum_{i=1}^{16}(x_i -\mu_\alpha)^2 \right) \right] \le k \)
And, simplifying yet more, we get:
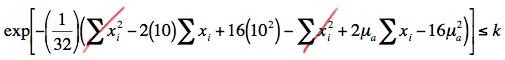
Taking the natural logarithm of both sides of the inequality, collecting like terms, and multiplying through by 32, we get:
\( -2(\mu_\alpha - 10) \sum x_i +16 (\mu_{\alpha}^{2} - 10^2) \le 32 ln(k) \)
Moving the constant term on the left-side of the inequality to the right-side, and dividing through by \(-16(2(\mu_\alpha - 10)) \), we get:
\( \dfrac{1}{16} \sum x_i \ge - \dfrac{1}{16(2(\mu_\alpha - 10))}(32 ln(k) - 16(\mu_{\alpha}^{2} - 10^2)) = k^* \)
In summary, we have shown that the ratio of the likelihoods is small, that is:
\(\dfrac{L(10)}{L(\mu_\alpha)} \le k \)
if and only if:
\( \bar{x} \ge k^*\)
Therefore, the best critical region of size \(\alpha\) for testing \(H_0: \mu = 10\) against each simple alternative \(H_A \colon \mu = \mu_a\), where \(\mu_a > 10\), is given by:
\( C= \left\{ (x_1, x_1, ... , x_n): \bar{x} \ge k^* \right\} \)
where \(k^*\) is selected such that the probability of committing a Type I error is \(\alpha\), that is:
\( \alpha = P(\bar{X} \ge k^*) \text{ when } \mu = 10 \)
Because the critical region C defines a test that is most powerful against each simple alternative \(\mu_a > 10\), this is a uniformly most powerful test, and C is a uniformly most powerful critical region of size \(\alpha\).