27.1 - A Definition and Simple Example
27.1 - A Definition and Simple ExampleThe title of this page is a little risky, as there are few simple examples when it comes to likelihood ratio testing! But, we'll work to make the example as simple as possible, namely by assuming again, unrealistically, that we know the population variance, but not the population mean. Before we state the definition of a likelihood ratio test, and then investigate our simple, but unrealistic, example, we first need to define some notation that we'll use throughout the lesson.
We'll assume that the probability density (or mass) function of X is \(f(x;\theta)\) where \(\theta\) represents one or more unknown parameters. Then:
- Let \(\Omega\) (greek letter "omega") denote the total possible parameter space of \(\theta\), that is, the set of all possible values of \(\theta\) as specified in totality in the null and alternative hypotheses.
- Let \(H_0 : \theta \in \omega\) denote the null hypothesis where \(\omega\) (greek letter "omega") is a subset of the parameter space \(\Omega\).
- Let \(H_A : \theta \in \omega'\) denote the alternative hypothesis where \(\omega '\) is the complement of \(\omega\) with respect to the parameter space \(\Omega\).
Let's make sure we are clear about that phrase "where \(\omega '\) is the complement of \(\omega\) with respect to the parameter space \(\Omega\)."
Example 27-1
If the total parameter space of the mean \(\mu\) is \(\Omega = {\mu: −∞ < \mu < ∞}\) and the null hypothesis is specified as \(H_0: \mu = 3\), how should we specify the alternative hypothesis so that the alternative parameter space is the complement of the null parameter space?
Answer
If the null parameter space is \(\Omega = {\mu: \mu = 3}\), then the alternative parameter space is everything that is in \(\Omega = {\mu: −∞ < \mu < ∞}\) that is not in \(\Omega\). That is, the alternative parameter space is \(\Omega ' = {\mu: \mu ≠ 3}\). And, so the alternative hypothesis is:
\(H_A : \mu \ne 3\)
In this case, we'd be interested in deriving a two-tailed test.
Example 27-2
If the alternative hypothesis is \(H_A: \mu > 3\), how should we (technically) specify the null hypothesis so that the null parameter space is the complement of the alternative parameter space?
Answer
If the alternative parameter space is (\omega ' = {\mu: \mu > 3}\), then the null parameter space is \(\omega = {\mu: \mu ≤ 3}\). And, so the null hypothesis is:
\(H_0 : \mu \le 3\)
Now, the reality is that some authors do specify the null hypothesis as such, even when they mean \(H_0: \mu = 3\). Ours don't, and so we won't. (That's why I put that "technically" in parentheses up above.) At any rate, in this case, we'd be interested in deriving a one-tailed test.
Definition. Let:
-
\(L(\hat{\omega})\) denote the maximum of the likelihood function with respect to \(\theta\) when \(\theta\) is in the null parameter space \(\omega\).
-
\(L(\hat{\Omega})\) denote the maximum of the likelihood function with respect to \(\theta\) when \(\theta\) is in the entire parameter space \(\Omega\).
Then, the likelihood ratio is the quotient:
\(\lambda = \dfrac{L(\hat{\omega})}{L(\hat{\Omega})}\)
And, to test the null hypothesis \(H_0 : \theta \in \omega\) against the alternative hypothesis \(H_A : \theta \in \omega'\), the critical region for the likelihood ratio test is the set of sample points for which:
\(\lambda = \dfrac{L(\hat{\omega})}{L(\hat{\Omega})} \le k\)
where \(0 < k < 1\), and k is selected so that the test has a desired significance level \(\alpha\).
Example 27-3

A food processing company packages honey in small glass jars. Each jar is supposed to contain 10 fluid ounces of the sweet and gooey good stuff. Previous experience suggests that the volume X, the volume in fluid ounces of a randomly selected jar of the company's honey is normally distributed with a known variance of 2. Derive the likelihood ratio test for testing, at a significance level of \(\alpha = 0.05\), the null hypothesis \(H_0: \mu = 10\) against the alternative hypothesis H_A: \mu ≠ 10\).
Answer
Because we are interested in testing the null hypothesis \(H_0: \mu = 10\) against the alternative hypothesis \(H_A: \mu ≠ 10\) for a normal mean, our total parameter space is:
\(\Omega =\left \{\mu : -\infty < \mu < \infty \right \}\)
and our null parameter space is:
\(\omega = \left \{10\right \}\)
Now, to find the likelihood ratio, as defined above, we first need to find \(L(\hat{\omega})\). Well, when the null hypothesis \(H_0: \mu = 10\) is true, the mean \(\mu\) can take on only one value, namely, \(\mu = 10\). Therefore:
\(L(\hat{\omega}) = L(10)\)
We also need to find \(L(\hat{\Omega})\) in order to define the likelihood ratio. To find it, we must find the value of \(\mu\) that maximizes \(L(\mu)\). Well, we did that back when we studied maximum likelihood as a method of estimation. We showed that \(\hat{\mu} = \bar{x}\) is the maximum likelihood estimate of \(\mu\). Therefore:
\(L(\hat{\Omega}) = L(\bar{x})\)
Now, putting it all together to form the likelihood ratio, we get:
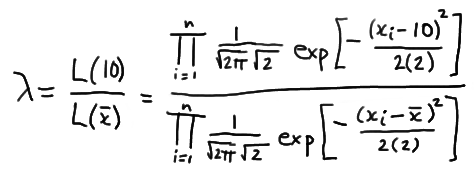
which simplifies to:
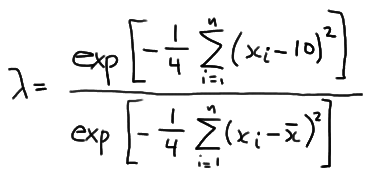
Now, let's step aside for a minute and focus just on the summation in the numerator. If we "add 0" in a special way to the quantity in parentheses:
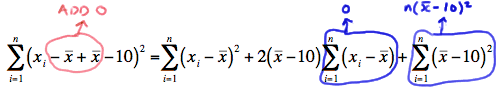
we can show that the summation can be written as:
\(\sum_{i=1}^{n}(x_i - 10)^2 = \sum_{i=1}^{n}(x_i - \bar{x})^2 + n(\bar{x} -10)^2 \)
Therefore, the likelihood ratio becomes:
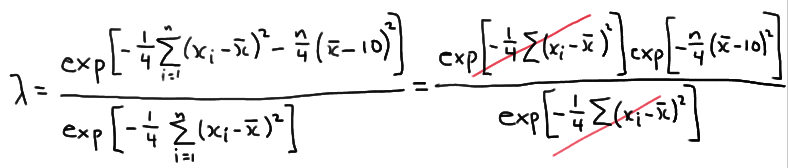
which greatly simplifies to:
\(\lambda = exp \left [-\dfrac{n}{4}(\bar{x}-10)^2 \right ]\)
Now, the likelihood ratio test tells us to reject the null hypothesis when the likelihood ratio \(\lambda\) is small, that is, when:
\(\lambda = exp\left[-\dfrac{n}{4}(\bar{x}-10)^2 \right] \le k\)
where k is chosen to ensure that, in this case, \(\alpha = 0.05\). Well, by taking the natural log of both sides of the inequality, we can show that \(\lambda ≤ k\) is equivalent to:
\( -\dfrac{n}{4}(\bar{x}-10)^2 \le \text{ln} k \)
which, by multiplying through by −4/n, is equivalent to:
\((\bar{x}-10)^2 \ge -\dfrac{4}{n} \text{ln} k \)
which is equivalent to:
\(\dfrac{|\bar{X}-10|}{\sigma / \sqrt{n}} \ge \dfrac{\sqrt{-(4/n)\text{ln} k}}{\sigma / \sqrt{n}} =k* \)
Aha! We should recognize that quantity on the left-side of the inequality! We know that:
\(Z = \dfrac{\bar{X}-10}{\sigma / \sqrt{n}} \)
follows a standard normal distribution when \(H_0: \mu = 10\). Therefore we can determine the appropriate \(k^*\) by using the standard normal table. We have shown that the likelihood ratio test tells us to reject the null hypothesis \(H_0: \mu = 10\) in favor of the alternative hypothesis \(H_A: \mu ≠ 10\) for all sample means for which the following holds:
\(\dfrac{|\bar{X}-10|}{ \sqrt{2} / \sqrt{n}} \ge z_{0.025} = 1.96 \)
Doing so will ensure that our probability of committing a Type I error is set to \(\alpha = 0.05\), as desired.