18.1 - The Basics
18.1 - The BasicsExample 18-1

Let's motivate the definition of a set of order statistics by way of a simple example.
Suppose a random sample of five rats yields the following weights (in grams):
\(x_1=602 \qquad x_2=781\qquad x_3=709\qquad x_4=742\qquad x_5=633\)
What are the observed order statistics of this set of data?
Answer
Well, without even knowing the formal definition of an order statistic, we probably don't need a rocket scientist to tell us that, in order to find the order statistics, we should probably arrange the data in increasing numerical order. Doing so, the observed order statistics are:
\(y_1=602<y_2=633<y_3=709<y_4=742<y_5=781\)
The only thing that might have tripped us up a bit in such a trivial example is if two of the rats had shared the same weight, as observing ties is certainly a possibility. We'll wash our hands of the likelihood of that happening, though, by making an assumption that will hold throughout this lesson... and beyond. We will assume that the n independent observations come from a continuous distribution, thereby making the probability zero that any two observations are equal. Of course, ties are still possible in practice. Making the assumption, though, that there is a near zero chance of a tie happening allows us to develop the distribution theory of order statistics that hold at least approximately even in the presence of ties. That said, let's now formally provide a definition for a set of order statistics.
Definition. If \(X_1, X_2, \cdots, X_n\) are observations of a random sample of size \(n\) from a continuous distribution, we let the random variables:
\(Y_1<Y_2<\cdots<Y_n\)
denote the order statistics of the sample, with:
- \(Y_1\) being the smallest of the \(X_1, X_2, \cdots, X_n\) observations
- \(Y_2\) being the second smallest of the \(X_1, X_2, \cdots, X_n\) observations
- ....
- \(Y_{n-1}\) being the next-to-largest of the \(X_1, X_2, \cdots, X_n\) observations
- \(Y_n\) being the largest of the \(X_1, X_2, \cdots, X_n\) observations
Now, what we want to do is work our way up to find the probability density function of any of the \(n\) order statistics, the \(r^{th}\) order statistic \(Y_r\). That way, we'd know how the order statistics behave and therefore could use that knowledge to draw conclusions about something like the fastest automobile in a race or the heaviest mouse on a certain diet. In finding the probability density function, we'll use the distribution function technique to do so. It's probably been a mighty bit since we used the technique, so in case you need a reminder, our strategy will be to first find the distribution function \(G_r(y)\) of the \(r^{th}\) order statistic, and then take its derivative to find the probability density function \(g_r(y)\) of the \(r^{th}\) order statistic. We're getting a little bit ahead of ourselves though. That's what we'll do on the next page. To make our work there more understandable, let's first take a look at a concrete example here.
Example 18-2
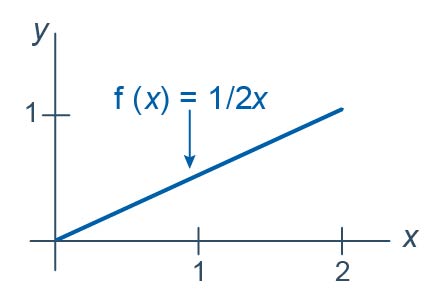
Let \(Y_1<Y_2<Y_3<Y_4<Y_5<Y_6\) be the order statistics associated with \(n=6\) independent observations each from the distribution with probability density function:
\(f(x)=\dfrac{1}{2}x\)
for \(0<x<2\). What is the probability that the next-to-largest order statistic, that is, \(Y_5\), is less than 1? That is, what is \(P(Y_5<1)\)?
Answer
The key to finding the desired probability is to recognize that the only way that the fifth order statistic, \(Y_5\), would be less than one is if at least 5 of the random variables \(X_1, X_2, X_3, X_4, X_5, \text{ and }X_6\) are less than one. For the sake of simplicity, let's suppose the first five observed values \(x_1, x_2, x_3, x_4, x_5\) are less than one, but the sixth \(x_6\) is not. In that case, the observed fifth-order statistic, \(y_5\), would be less than one:
The observed fifth order statistic, \(y_5\), would also be less than one if all six of the observed values \(x_1, x_2, x_3, x_4, x_5, x_6\) are less than one:
The observed fifth order statistic, \(y_5\), would not be less than one if the first four observed values \(x_1, x_2, x_3, x_4\) are less than one, but the fifth \(x_5\) and sixth \(x_6\) is not:
Again, the only way that the fifth order statistic, \(Y_5\), would be less than one is if 5 or 6... that is, at least 5... of the random variables \(X_1, X_2, X_3, X_4, X_5, \text{ and }X_6\) are less than one. For the sake of simplicity, we considered just the first five or six random variables, but in reality, any five or six random variables less than one would do. We just have to do some "choosing" to count the number of ways that we can get any five or six of the random variables to be less than one.
If you think about it, then, we have a binomial probability calculation here. If the event \(\{X_i<1\}\), \(i=1, 2, \cdots, 5\) is considered a "success," and we let \(Z\) = the number of successes in six mutually independent trials, then \(Z\) is a binomial random variable with \(n=6\) and \(p=0.25\):
\(P(X_i\le1)=\dfrac{1}{2}\int_{0}^{1}x dx=\dfrac{1}{2}\left[\dfrac{x^2}{2}\right]_{x=0}^{x=1}=\dfrac{1}{2}\left(\dfrac{1}{2}-0\right)=\dfrac{1}{4}\)
Finding the probability that the fifth order statistic, \(Y_5\), is less than one reduces to a binomial calculation then. That is:
\(P(Y_5<1)=P(Z=5)+P(Z=6)=\binom{6}{5}\left(\dfrac{1}{4} \right)^5\left(\dfrac{3}{4} \right)^1+\binom{6}{6}\left(\dfrac{1}{4} \right)^6\left(\dfrac{3}{4} \right)^0=0.0046\)
The fact that the calculated probability is so small should make sense in light of the given p.d.f. of \(X\). After all, each individual \(X_i\) has a greater chance of falling above, rather than below, one. For that reason, it would unusual to observe as many as five or six \(X\)'s less than one.
What is the cumulative distribution function \(G_5(y)\) of the fifth order statistic \(Y_5\)?
Answer
Recalling the definition of a cumulative distribution function, \(G_5(y)\) is defined to be the probability that the fifth order statistic \(Y_5\) is less than some value \(y\). That is:
\(G_5(y)=P(Y_5 < y)\)
Well, in our above work, we found the probability that the fifth order statistic \(Y_5\) is less than a specific value, namely 1. We just need to generalize our work there to allow for any value \(y\). Well, if the event \(\{X_i<y\}\), \(i=1, 2, \cdots, 5\) is considered a "success," and we let \(Z\) = the number of successes in six mutually independent trials, then \(Z\) is a binomial random variable with \(n=6\) and probability of success:
\(P(X_i\le y)=\dfrac{1}{2}\int_{0}^{y}x dx=\dfrac{1}{2}\left[\dfrac{x^2}{2}\right]_{x=0}^{x=y}=\dfrac{1}{2}\left(\dfrac{y^2}{2}-0\right)=\dfrac{y^2}{4}\)
Therefore, the cumulative distribution function \(G_5(y)\) of the fifth order statistic \(Y_5\) is:
\(G_5(y)=P(Y_5 < y)=P(Z=5)+P(Z=6)=\binom{6}{5}\left(\dfrac{y^2}{4}\right)^5\left(1-\dfrac{y^2}{4}\right)+\left(\dfrac{y^2}{4}\right)^6\)
for \(0<y<2\).
What is the probability density function \(g_5(y)\) of the fifth order statistic \(Y_5\)?
Answer
All we need to do to find the probability density function \(g_{5}(y)\) is to take the derivative of the distribution function \(G_5(y)\) with respect to \(y\). Doing so, we get:
\(g_5(y)=G_{5}^{'}(y)=\binom{6}{5}\left(\dfrac{y^2}{4}\right)^5\left(\dfrac{-2y}{4}\right)+\binom{6}{5}\left(1-\dfrac{y^2}{4}\right)5\left(\dfrac{y^2}{4}\right)^4\left(\dfrac{2y}{4}\right)+6\left(\dfrac{y^2}{4}\right)^5\left(\dfrac{2y}{4}\right)\)
Upon recognizing that:
\(\binom{6}{5}=6\) and \(\binom{6}{5}\times5=\dfrac{6!}{5!1!}\times5=\dfrac{6!}{4!1!}\)
we see that the middle term simplifies somewhat, and the first term is just the negative of the third term, therefore they cancel each other out:
\(g_{5}(y)=\left(\begin{array}{l}
6 \\
5
\end{array}\right)\color{red}\cancel {\color{black}\left(\frac{y^{2}}{4}\right)^{5}\left(\frac{-2 y}{4}\right)}\color{black}+\frac{6 !}{4 ! 1 !}\left(1-\frac{y^{2}}{4}\right)\left(\frac{y^{2}}{4}\right)^{4}\left(\frac{2 y}{4}\right)+\color{red}\cancel {\color{black}6\left(\frac{y^{2}}{4}\right)^{5}\left(\frac{2 y}{4}\right)}\)
Therefore, the probability density function of the fifth order statistic \(Y_5\) is:
\(g_5(y)=\dfrac{6!}{4!1!}\left(1-\dfrac{y^2}{4}\right)\left(\dfrac{y^2}{4}\right)^4\left(\dfrac{1}{2}y\right)\)
for \(0<y<2\). When we go on to generalize our work on the next page, it will benefit us to note that because the density function and distribution function of each \(X\) are:
\(f(x)=\dfrac{1}{2}x\) and \(F(x)=\dfrac{x^2}{4}\)
respectively, when \(0<x<2\), we can alternatively write the probability density function of the fifth order statistic \(Y_5\) as:
\(g_5(y)=\dfrac{6!}{4!1!}\left[F(y)\right]^4\left[1-F(y)\right]f(y)\)
Done!
Whew! Now, let's push on to the more general case of finding the probability density function of the \(r^{th}\) order statistic.