Lesson 4: Sampling Distributions
Lesson 4: Sampling DistributionsOverview
In inferential statistics, we want to use characteristics of the sample (i.e. a statistic) to estimate the characteristics of the population (i.e. a parameter).
In Lesson 3, we learned how to define events as random variables. By doing so, we can understand events mathematically by using probability functions, means, and standard deviations. All of this is important because it helps us reach our goal to be able to make inferences about the population based on the sample. But we need more.
If we obtain a random sample and calculate a sample statistic from that sample, the sample statistic is a random variable (wow!). The population parameters, however, are fixed. If the statistic is a random variable, can we find the distribution? The mean? The standard deviation?
The answer is yes! This is why we need to study the sampling distribution of statistics. So what is a sampling distribution?
- Sampling Distribution
- The sampling distribution of a statistic is a probability distribution based on a large number of samples of size \(n\) from a given population.
Consider this example. A large tank of fish from a hatchery is being delivered to the lake. We want to know the average length of the fish in the tank. Instead of measuring all of the fish, we randomly sample twenty fish and use the sample mean to estimate the population mean.
Denote the sample mean of the twenty fish as \(\bar{x}_1\). Suppose we take a separate sample of size twenty from the same hatchery. Denote that sample mean as \(\bar{x}_2\). Would \(\bar{x}_1\) equal \(\bar{x}_2\)? Not necessarily. What if we took another sample and found the mean? Consider now taking 1000 random samples of size twenty and recording all of the sample means. We could take the 1000 sample means and create a histogram. This would give us a picture of what the distribution of the sample means looks like. The distribution of all of these sample means is the sampling distribution of the sample mean.
We can find the sampling distribution of any sample statistic that would estimate a certain population parameter of interest. In this Lesson, we will focus on the sampling distributions for the sample mean, \(\bar{x}\), and the sample proportion, \(\hat{p}\).
We begin by describing the sampling distribution of the sample mean and then applying the central limit theorem. Last, we will discuss the sampling distribution of the sample proportion.
Objectives
- Understand the meaning of sampling distribution.
- Apply the central limit theorem to calculate approximate probabilities for sample means and sample proportions.
- Describe the sampling distribution of the sample mean and proportion.
- Identify situations in which the normal distribution and t-distribution may be used to approximate a sampling distribution.
4.1 - Sampling Distribution of the Sample Mean
4.1 - Sampling Distribution of the Sample MeanIn the following example, we illustrate the sampling distribution for the sample mean for a very small population. The sampling method is done without replacement.
Sample Means with a Small Population: Pumpkin Weights

In this example, the population is the weight of six pumpkins (in pounds) displayed in a carnival "guess the weight" game booth. You are asked to guess the average weight of the six pumpkins by taking a random sample without replacement from the population.
|
Pumpkin |
A |
B |
C |
D |
E |
F |
|---|---|---|---|---|---|---|
|
Weight (in pounds) |
19 |
14 |
15 |
9 |
10 |
17 |
Since we know the weights from the population, we can find the population mean.
\(\mu=\dfrac{19+14+15+9+10+17}{6}=14\) pounds
To demonstrate the sampling distribution, let’s start with obtaining all of the possible samples of size \(n=2\) from the populations, sampling without replacement. The table below shows all the possible samples, the weights for the chosen pumpkins, the sample mean and the probability of obtaining each sample. Since we are drawing at random, each sample will have the same probability of being chosen.
|
Sample |
Weight |
\(\boldsymbol{\bar{x}}\) |
Probability |
|---|---|---|---|
|
A, B |
19, 14 |
16.5 |
\(\frac{1}{15}\) |
|
A, C |
19, 15 |
17.0 |
\(\frac{1}{15}\) |
|
A, D |
19, 9 |
14.0 |
\(\frac{1}{15}\) |
|
A, E |
19, 10 |
14.5 |
\(\frac{1}{15}\) |
|
A, F |
19, 17 |
18.0 |
\(\frac{1}{15}\) |
|
B, C |
14, 15 |
14.5 |
\(\frac{1}{15}\) |
|
B, D |
14, 9 |
11.5 |
\(\frac{1}{15}\) |
|
B, E |
14, 10 |
12.0 |
\(\frac{1}{15}\) |
|
B, F |
14, 17 |
15.5 |
\(\frac{1}{15}\) |
|
C, D |
15, 9 |
12.0 |
\(\frac{1}{15}\) |
|
C, E |
15, 10 |
12.5 |
\(\frac{1}{15}\) |
|
C, F |
15, 17 |
16.0 |
\(\frac{1}{15}\) |
|
D, E |
9, 10 |
9.5 |
\(\frac{1}{15}\) |
|
D, F |
9, 17 |
13.0 |
\(\frac{1}{15}\) |
|
E, F |
10, 17 |
13.5 |
\(\frac{1}{15}\) |
We can combine all of the values and create a table of the possible values and their respective probabilities.
|
\(\boldsymbol{\bar{x}}\) |
9.5 |
11.5 |
12.0 |
12.5 |
13.0 |
13.5 |
14.0 |
14.5 |
15.5 |
16.0 |
16.5 |
17.0 |
18.0 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Probability |
\(\frac{1}{15}\) |
\(\frac{1}{15}\) |
\(\frac{2}{15}\) |
\(\frac{1}{15}\) |
\(\frac{1}{15}\) |
\(\frac{1}{15}\) |
\(\frac{1}{15}\) |
\(\frac{2}{15}\) |
\(\frac{1}{15}\) |
\(\frac{1}{15}\) |
\(\frac{1}{15}\) |
\(\frac{1}{15}\) |
\(\frac{1}{15}\) |
The table is the probability table for the sample mean and it is the sampling distribution of the sample mean weights of the pumpkins when the sample size is 2. It is also worth noting that the sum of all the probabilities equals 1. It might be helpful to graph these values.
One can see that the chance that the sample mean is exactly the population mean is only 1 in 15, very small. (In some other examples, it may happen that the sample mean can never be the same value as the population mean.) When using the sample mean to estimate the population mean, some possible error will be involved since the sample mean is random.
Now that we have the sampling distribution of the sample mean, we can calculate the mean of all the sample means. In other words, we can find the mean (or expected value) of all the possible \(\bar{x}\)’s.
The mean of the sample means is
\(\mu_\bar{x}=\sum \bar{x}_{i}f(\bar{x}_i)=9.5\left(\frac{1}{15}\right)+11.5\left(\frac{1}{15}\right)+12\left(\frac{2}{15}\right)\\+12.5\left(\frac{1}{15}\right)+13\left(\frac{1}{15}\right)+13.5\left(\frac{1}{15}\right)+14\left(\frac{1}{15}\right)\\+14.5\left(\frac{2}{15}\right)+15.5\left(\frac{1}{15}\right)+16\left(\frac{1}{15}\right)+16.5\left(\frac{1}{15}\right)\\+17\left(\frac{1}{15}\right)+18\left(\frac{1}{15}\right)=14\)
Even though each sample may give you an answer involving some error, the expected value is right at the target: exactly the population mean. In other words, if one does the experiment over and over again, the overall average of the sample mean is exactly the population mean.
Now, let's do the same thing as above but with sample size \(n=5\)
|
Sample |
Weights |
\(\boldsymbol{\bar{x}}\) |
Probability |
|---|---|---|---|
|
A, B, C, D, E |
19, 14, 15, 9, 10 |
13.4 |
1/6 |
|
A, B, C, D, F |
19, 14, 15, 9, 17 |
14.8 |
1/6 |
|
A, B, C, E, F |
19, 14, 15, 10, 17 |
15.0 |
1/6 |
|
A, B, D, E, F |
19, 14, 9, 10, 17 |
13.8 |
1/6 |
|
A, C, D, E, F |
19, 15, 9, 10, 17 |
14.0 |
1/6 |
|
B, C, D, E, F |
14, 15, 9, 10, 17 |
13.0 |
1/6 |
The sampling distribution is:
|
\(\boldsymbol{\bar{x}}\) |
13.0 |
13.4 |
13.8 |
14.0 |
14.8 |
15.0 |
|---|---|---|---|---|---|---|
|
Probability |
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
The mean of the sample means is...
\(\mu=(\dfrac{1}{6})(13+13.4+13.8+14.0+14.8+15.0)=14\) pounds
The following dot plots show the distribution of the sample means corresponding to sample sizes of \(n=2\) and of \(n=5\).
Again, we see that using the sample mean to estimate population mean involves sampling error. However, the error with a sample of size \(n=5\) is on the average smaller than with a sample of size \(n= 2\).
Sampling Error and Size
- Sampling Error
- The error resulting from using a sample characteristic to estimate a population characteristic.
Sample size and sampling error: As the dotplots above show, the possible sample means cluster more closely around the population mean as the sample size increases. Thus, the possible sampling error decreases as sample size increases.
What happens when the population is not small, as in the pumpkin example?
Sample Means with Large Samples: Exam Example

An instructor of an introduction to statistics course has 200 students. The scores out of 100 points are shown in the histogram.
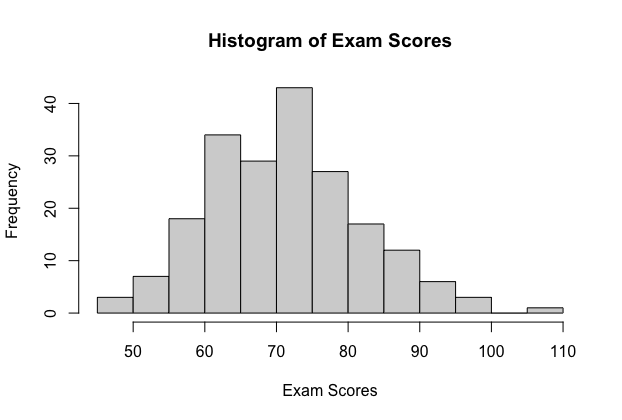
The population mean is \(μ=71.18\) and the population standard deviation is \(σ=10.73\)
Let's demonstrate the sampling distribution of the sample means using the StatKey website. The first video will demonstrate the sampling distribution of the sample mean when n = 10 for the exam scores data. The second video will show the same data but with samples of n = 30.
You should start to see some patterns. The mean of the sampling distribution is very close to the population mean. The standard deviation of the sampling distribution is smaller than the standard deviation of the population.
In the examples so far, we were given the population and sampled from that population.
What happens when we do not have the population to sample from? What happens when all that we are given is the sample? Fortunately, we can use some theory to help us. The mathematical details of the theory are beyond the scope of this course but the results are presented in this lesson.
In the next two sections, we will discuss the sampling distribution of the sample mean when the population is Normally distributed and when it is not.
4.1.1 - Population is Normal
4.1.1 - Population is NormalIf the population is normally distributed with mean \(\mu\) and standard deviation \(\sigma\), then the sampling distribution of the sample mean is also normally distributed no matter what the sample size is. When the sampling is done with replacement or if the population size is large compared to the sample size, then \(\bar{x}\) has mean \(\mu\) and standard deviation \(\dfrac{\sigma}{\sqrt{n}}\). We use the term standard error for the standard deviation of a statistic, and since sample average, \(\bar{x}\) is a statistic, standard deviation of \(\bar{x}\) is also called standard error of \(\bar{x}\). However, in some books you may find the term standard error for the estimated standard deviation of \(\bar{x}\). In this class we use the former definition, that is, standard error of \(\bar{x}\) is the same as standard deviation of \(\bar{x}\).
- Standard Deviation of \(\boldsymbol{\bar{x}}\) [Standard Error]
- \(SD(\bar{X})=SE(\bar{X})=\dfrac{\sigma}{\sqrt{n}}\)
When we know the sample mean is Normal or approximately Normal, then we can calculate a z-score for the sample mean and determine probabilities for it using:
- Z-Score of the Sample Mean
- \(z=\dfrac{\bar{x}-\mu}{\dfrac{\sigma}{\sqrt{n}}}\)
Example 4-1: Speedboat Engines
The engines made by Ford for speedboats have an average power of 220 horsepower (HP) and standard deviation of 15 HP. You can assume the distribution of power follows a normal distribution.
Consumer Reports® is testing the engines and will dispute the company's claim if the sample mean is less than 215 HP. If they take a sample of 4 engines, what is the probability the mean is less than 215?
Answer
We want to find \(P(\bar{X}<215)\).
Since the population follows a normal distribution, we can conclude that \(\bar{X}\) has a normal distribution with mean 220 HP (\(\mu=220\)) and a standard deviation of \(\dfrac{\sigma}{\sqrt{n}}=\dfrac{15}{\sqrt{4}}=7.5\)HP.
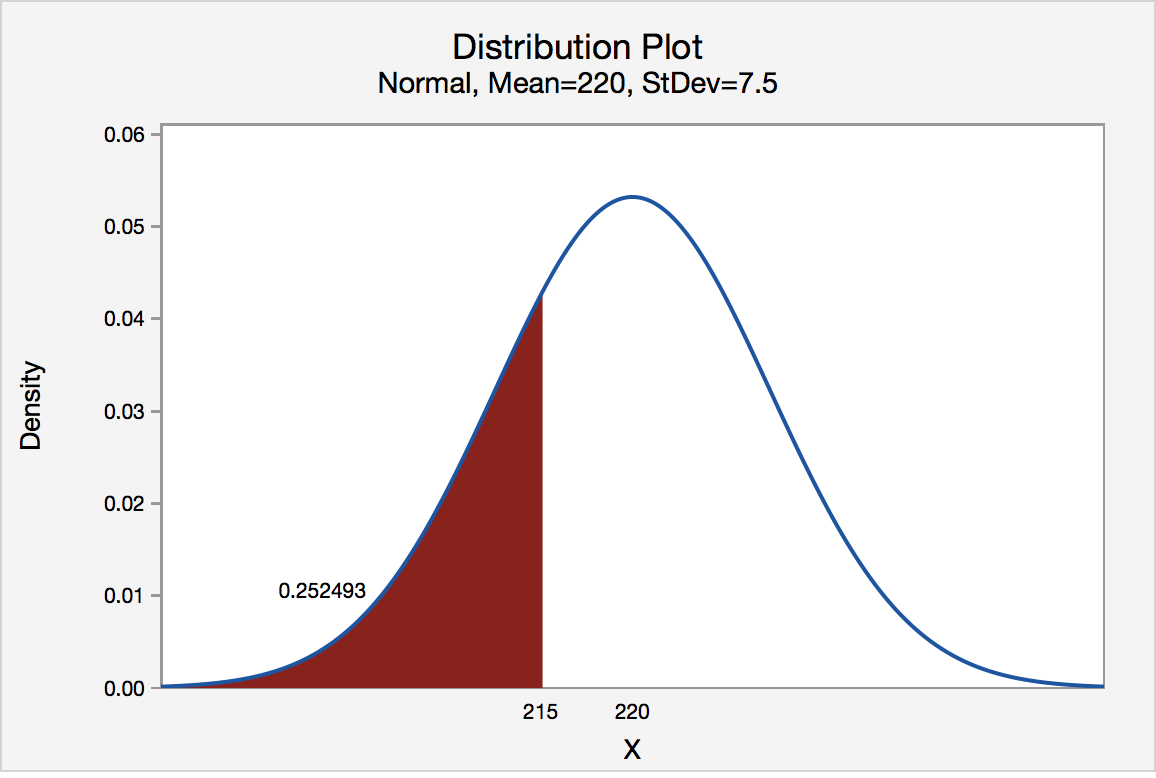
\(P(\bar{X}<215)=P\left(Z<\dfrac{215-220}{7.5}\right)=P(Z<-0.67) \approx\ 0.2514\)
If Consumer Reports® samples four engines, the probability that the mean is less than 215 HP is 25.14%.
Try It!
Using the speedboat engines example above, answer the following question.
If Consumer Reports® samples 100 engines, what is the probability that the sample mean will be less than 215?
The sampling distribution of the sample mean is Normal with mean \(\mu=220\) and standard deviation \(\dfrac{\sigma}{\sqrt{n}}=\dfrac{15}{\sqrt{100}}=1.5\).
\(P(\bar{X}<215)=P\left(\dfrac{\bar{X}-\mu}{\dfrac{\sigma}{\sqrt{n}}}<\dfrac{215-220}{1.5}\right)=P\left(Z<-\dfrac{10}{3}\right)=0.00043\).
It is worth noting the difference in the probabilities here. When the sample size is \(n=4\), the probability of obtaining a sample mean of 215 or less is 25.14%. When the sample size is \(n=100\), the probability is 0.043%.
4.1.2 - Population is Not Normal
4.1.2 - Population is Not NormalCentral Limit Theorem
What happens when the sample comes from a population that is not normally distributed? This is where the Central Limit Theorem comes in.
For a large sample size (we will explain this later), \(\bar{x}\) is approximately normally distributed, regardless of the distribution of the population one samples from. If the population has mean \(\mu\) and standard deviation \(\sigma\), then \(\bar{x}\) has mean \(\mu\) and standard deviation \(\dfrac{\sigma}{\sqrt{n}}\).
We should stop here to break down what this theorem is saying because the Central Limit Theorem is very powerful!
The Central Limit Theorem applies to a sample mean from any distribution. We could have a left-skewed or a right-skewed distribution. As long as the sample size is large, the distribution of the sample means will follow an approximate Normal distribution.
For the purposes of this course, a sample size of \(n>30\) is considered a large sample.
CLT Demonstration
Before we begin the demonstration, let's talk about what we should be looking for…
Notes on the CLT for this demonstration:
- If the population is skewed and sample size small, then the sample mean won't be normal.
- When doing a simulation, one replicates the process many times. Using 10,000 replications is a good idea.
- If the population is normal, then the distribution of sample mean looks normal even if \(n = 2\). Note the app in the video used capital N for the sample size.
- If the population is skewed, then the distribution of sample mean looks more and more normal when \(n\) gets larger.
- Note that in all cases, the mean of the sample mean is close to the population mean and the standard error of the sample mean is close to \(\dfrac{\sigma}{\sqrt{n}}\).
Sampling Distribution of the Sample Mean
With the Central Limit Theorem, we can finally define the sampling distribution of the sample mean.
- Sampling Distribution of the Sample Mean
-
The sampling distribution of the sample mean will have:
- The same mean as the population mean, \(\mu\).
- Standard deviation [standard error] of \(\dfrac{\sigma}{\sqrt{n}}\).
It will be Normal (or approximately Normal) if either of these conditions is satisfied:
- The population distribution is Normal.
- The sample size is large (\(n \gt 30\)).
Example 4-2: Weights of Baby Giraffes

The weights of baby giraffes are known to have a mean of 125 pounds and a standard deviation of 15 pounds.
If we obtained a random sample of 40 baby giraffes,
- what is the probability that the sample mean will be between 120 and 130 pounds?
- what is the 75th percentile of the sample means of size \(n=40\)?
Answer
Does the problem indicate that the distribution of weights is normal? No, it does not. In order to apply the Central Limit Theorem, we need a large sample. Since \(n=40>30\), we can use the theorem. The sampling distribution of the sample mean is approximately Normal with mean \(\mu=125\) and standard error \(\dfrac{\sigma}{\sqrt{n}}=\dfrac{15}{\sqrt{40}}\).
- We want \(P(120<\bar{X}<130)\).
\begin{align} P(120<\bar{X}<130) &=P\left(\dfrac{120-125}{\dfrac{15}{\sqrt{40}}}<\dfrac{\bar{X}-\mu}{\dfrac{\sigma}{\sqrt{n}}}<\frac{130-125}{\dfrac{15}{\sqrt{40}}}\right)\\ &=P(-2.108<Z<2.108)\\&=P(Z<2.108)-P(Z<-2.108)\\ &=0.9826-0.0174\\ &=0.9652 \end{align}
The probability that the sample mean of the 40 giraffes is between 120 and 130 lbs is 96.52%.
-
To find the 75th percentile, we need the value \(a\) such that \(P(Z<a)=0.75\). Using the Z-table or software, we get \(a=.6745\). The formula for the z-score is...
\(z=\dfrac{\bar{X}-\mu}{\dfrac{\sigma}{\sqrt{40}}}=\dfrac{\bar{X}-125}{\dfrac{15}{\sqrt{40}}}\)
Since we know the \(z\) value is 0.6745, we can use algebra to solve for \(\bar{X}\).
\begin{align} 0.6745&=\dfrac{\bar{X}-125}{\frac{15}{\sqrt{40}}}\\
0.6745\left(\frac{15}{\sqrt{40}}\right) &=\bar{X}-125\\
\bar{X}&=0.6745\left(\frac{15}{\sqrt{40}}\right)+125\\&=126.6 \end{align}The 75th percentile of all the sample means of size \(n=40\) is \(126.6\) pounds.
4.2 - Sampling Distribution of the Sample Proportion
4.2 - Sampling Distribution of the Sample ProportionBefore we begin, let’s make sure we review the terms and notation associated with proportions:
- \(p\) is the population proportion. It is a fixed value.
- \(n\) is the size of the random sample.
- \(\hat{p}\) is the sample proportion. It varies based on the sample.
The following example will illustrate how to find the sampling distribution for an example where the population is small.
Sample Proportions with a Small Population: Favorite Color

In a particular family, there are five children. Their names are Alex (A), Betina (B), Carly (C), Debbie (D), and Edward (E). The table below shows the child’s name and their favorite color.
|
Name |
Alex (A) |
Betina (B) |
Carly (C) |
Debbie (D) |
Edward (E) |
|---|---|---|---|---|---|
|
Color |
Green |
Blue |
Yellow |
Purple |
Blue |
We are interested in the proportion of children in the family who prefer the color blue, and from the table, we can see that \(p = .40\) of the children prefer blue.
Similar to the pumpkin example earlier in the lesson, let's say we didn't know the proportion of children who like blue as their favorite color. We'll use resampling methods to estimate the proportion. Let’s take \(n=2\) repeated samples, taken without replacement. Here are all the possible samples of size \(n=2\) and their respective probabilities of the proportion of children who like blue.
|
Sample |
P(Blue) |
Probability |
|---|---|---|
|
AB |
1/2 |
1/10 |
|
AC |
0 |
1/10 |
|
AD |
0 |
1/10 |
|
AE |
1/2 |
1/10 |
|
BC |
1/2 |
1/10 |
|
BD |
1/2 |
1/10 |
|
BE |
1 |
1/10 |
|
CD |
0 |
1/10 |
|
CE |
1/2 |
1/10 |
|
DE |
1/2 |
1/10 |
The probability mass function (PMF) is:
|
P(Blue) |
0 |
1/2 |
1 |
|---|---|---|---|
|
Probability |
3/10 |
6/10 |
1/10 |
The graph of the PMF:
Sampling Distribution of P(Blue)
Bar graph showing three bars (0 with a length of 0.3, 0.5 with length of 0.5 and 1 with a lenght of 0.1).
The true proportion is \(p=P(Blue)=\frac{2}{5}\). When the sample size is \(n=2\), you can see from the PMF, it is not possible to get a sampling proportion that is equal to the true proportion.
Although not presented in detail here, we could find the sampling distribution for a larger sample size, say \(n=4\). The PMF for n=4 is...
|
P(Blue) |
1/4 |
1/2 |
|---|---|---|
|
Probability |
2/5 |
3/5 |
As with the sampling distribution of the sample mean, the sampling distribution of the sample proportion will have sampling error. It is also the case that the larger the sample size, the smaller the spread of the distribution.
Example 4-3 Resampling with StatKey
Using StatKey, we resample 1000 times from populations that have probabilities of success, 0.1, 0.9, and 0.5 respectively with a sample size of $n=25$. The video shows the resulting distributions.
4.2.1 - Normal Approximation to the Binomial
4.2.1 - Normal Approximation to the BinomialFor the sampling distribution of the sample mean, we learned how to apply the Central Limit Theorem when the underlying distribution is not normal. In this section, we will present how we can apply the Central Limit Theorem to find the sampling distribution of the sample proportion. Let’s start by defining a Bernoulli random variable, \(Y\).
- Bernoulli Random Variable \(\boldsymbol{Y}\)
-
For an experiment that results in a success or a failure, let the random variable \(Y\) equal 1, if there is a success, and 0 if there is a failure. Therefore,
\(Y=\begin{cases} 1 & \text{success}\\ 0 & \text{failure}\end{cases}\)
and let \(p\) be the probability of a success.
The Bernoulli random variable is a special case of the Binomial random variable, where the number of trials is equal to one.
Suppose we have, say \(n\), independent trials of this same experiment. Then we would have \(n\) values of \(Y\), namely \(Y_1, Y_2, ...Y_n\).
If we define \(X\) to be the sum of those values, we get...
\(X=\sum_{i=1}^n Y_i\)
\(X\) is then a Binomial random variable with parameters \(n\) and \(p\).
You are probably wondering what this has to do with the sampling distribution of the sample proportion. Well, suppose we have a random sample of size \(n\) from a population and are interested in a particular "success". Let the probability of success be \(p\). We can label the successes as 1 and the failures as 0. The sample proportion, \(\hat{p}\) would be the sum of all the successes divided by the number in our sample. Therefore,
\(\hat{p}=\dfrac{\sum_{i=1}^n Y_i}{n}=\dfrac{X}{n}\)
In other words, \(\hat{p}\) could be thought of as a mean! If this is the case, we can apply the Central Limit Theorem for large samples!
Therefore, for large samples, the shape of the sampling distribution for $\hat{p}$ will be approximately normal. What about the mean and the standard deviation?
- Mean and Standard Deviation [Standard Error] of \(\hat{p}\)
-
Given X is binomial...
- The mean of \(\hat{p}\)
The mean of \(\hat{p}\) would just be \(p\) since the mean of \(X\) is \(\mu=np\) and \(\hat{p}=\dfrac{X}{n}\).
- The standard deviation [standard error] of \(\hat{p}\)
The standard error of \(\hat{p}\) is \(\sqrt{\dfrac{p(1-p)}{n}}\) since the standard deviation of \(X\) is \(\sqrt{np(1-p)}\).
- The mean of \(\hat{p}\)
4.2.2 - Sampling Distribution of the Sample Proportion
4.2.2 - Sampling Distribution of the Sample ProportionThe distribution of the sample proportion approximates a normal distribution under the following 2 conditions.
Over the years the values of the conditions have changed. The examples that follow in the remaining lessons will use the first set of conditions at 5, however, you may come across other books or software that may use 10 or 15 for this value.
- \(np \geq 5\)
- \(n(1−p) \geq 5\)
- \(np \geq 10\)
- \(n(1−p) \geq 10\)
- \(np \geq 15 \)
- \(n(1-p) \geq 15 \)
If any set of the two conditions listed above are satisfied, the sampling distribution of the sample proportion is...
- approximately normal
- with mean, \(\mu=p\)
- standard deviation [standard error], \(\sigma=\sqrt{\dfrac{p(1-p)}{n}}\)
If the sampling distribution of \(\hat{p}\) is approximately normal, we can convert a sample proportion to a z-score using the following formula:
\(z=\dfrac{\hat{p}-p}{\sqrt{\dfrac{p(1-p)}{n}}}\)
We can apply this theory to find probabilities involving sample proportions.
Example 4-4: iPhone Users

Suppose it is known that 43% of Americans own an iPhone. If a random sample of 50 Americans were surveyed, what is the probability that the proportion of the sample who owned an iPhone is between 45% and 50%?
For this problem, we know $p=0.43$ and $n=50$. First, we should check our conditions for the sampling distribution of the sample proportion.
\(np=50(0.43)=21.5\) and \(n(1-p)=50(1-0.43)=28.5\) - both are greater than 5.
Since the conditions are satisfied, $\hat{p}$ will have a sampling distribution that is approximately normal with mean \(\mu=0.43\) and standard deviation [standard error] \(\sqrt{\dfrac{0.43(1-0.43)}{50}}\approx 0.07\).
\begin{align} P(0.45<\hat{p}<0.5) &=P\left(\frac{0.45-0.43}{0.07}< \frac{\hat{p}-p}{\sqrt{\frac{p(1-p)}{n}}}<\frac{0.5-0.43}{0.07}\right)\\ &\approx P\left(0.286<Z<1\right)\\ &=P(Z<1)-P(Z<0.286)\\ &=0.8413-0.6126\\ &=0.2287\end{align}
Therefore, if the true proportion of Americans who own an iPhone is 43%, then there would be a 22.87% chance that we would see a sample proportion between 45% and 50% when the sample size is 50.
Try it!
If a random sample of size of seventy five was surveyed, what is the probability we would find more than 50% of Americans with an iPhone?
\begin{align}P\left(\hat{p}>0.5\right) &=\left(\frac{\hat{p}}{\sqrt{\frac{p(1-p)}{n}}}>\frac{0.5-0.43}{\sqrt{\frac{0.43(1-0.43)}{75}}}\right)\\ &\approx P\left(Z>1.22\right)\\&=1-P(Z<1.22)\\&=1-0.8888\\&=0.1112 \end{align}
Therefore, there is a 11.1% chance to get a sample proportion of 50% or higher in a sample size of 75.4.3 - Lesson 4 Summary
4.3 - Lesson 4 SummaryIn this Lesson, we learned how to use the Central Limit Theorem to find the sampling distribution for the sample mean and the sample proportion under certain conditions.
We learned that the sampling distributions are centered around the population parameter with variability. All of this theory was built knowing the parameter. Can we use this information in situations where the parameter is unknown?
The answer is yes! In the next lesson, we take our first step into inference and into the “real world” where the population parameters are unknown and need to be estimated.