Lesson 5: Confidence Intervals
Lesson 5: Confidence IntervalsOveriew
Introduction to Inferences
So far, we learned how to collect and summarize data (Lesson 1). Then we learned how to quantify the likelihood of events using probability (Lesson 2). Next, we learned how to model these events as random variables (Lesson 3). In the previous Lesson, we learned how to find the sampling distributions of sample statistics (Lesson 4).
In Lesson 4, the sampling distributions for the sample statistics assumed we knew the population parameters (fantasy land). In real life, we do not know these parameters (or we would not need statistics!). In this lesson, we switch from "fantasy land" to real life. We know what to do when the parameters are known, let's see how we can use that information when they are unknown.
Objectives
- Describe the role of statistical inference in estimation in terms of the population and sample.
- Explain the general form of a confidence interval and apply it to different statistics and conditions.
- Construct a confidence interval to estimate a population mean or proportion.
- Given a confidence interval, interpret the meaning in terms of the population.
- Identify when to use the t-distribution as opposed to the normal distribution given the sample size and population distribution.
- Define and interpret the margin of error.
- Given the population standard deviation and a confidence level, calculate the required sample size needed to obtain the desired margin of error.
5.1 - Introduction to Inferences
5.1 - Introduction to InferencesThe real power of statistics comes from applying the concepts of probability to situations where you have data but not necessarily the whole population. The results, called statistical inference, give you probability statements about the population of interest based on that set of data.
Types of Statistical Inference
There are two types of statistical inferences: Estimation and Statistical Tests.
- Estimation
-
Use information from the sample to estimate (or predict) the parameter of interest.
For instance, using the result of a poll about the president's current approval rating to estimate (or predict) his or her true current approval rating nationwide.
- Statistical Tests
-
Use information from the sample to determine whether a certain statement about the parameter of interest is true. Statistical tests are also referred to as hypothesis tests.
For instance, suppose a news station claims that the President’s current approval rating is more than 75%. We want to determine whether that statement is supported by the poll data.
5.2 - Estimation and Confidence Intervals
5.2 - Estimation and Confidence IntervalsEstimation
Two common estimation methods are point and interval estimates.
- Point Estimates
- An estimate for a parameter that is one numerical value. An example of a point estimate is the sample mean or the sample proportion.
- Interval Estimates
- Interval estimates give an interval as the estimate for a parameter. This is a new concept which is the focus of this lesson. Such intervals are built around point estimates which is why understanding point estimates is important to understanding interval estimates.
In this course, the interval estimates we find are referred to as confidence intervals.
- Confidence Interval
- An interval of values computed from sample data that is likely to cover the true parameter of interest.
There are many estimators for population parameters. For example, if we want to know the "center" of a distribution, why use the mean? Could we use the median? How about using the middle value, i.e. (max+min)/2? We choose particular estimators for various reasons with information based on their sampling distributions. Here are some properties of "good" estimators.
Properties of 'Good' Estimators
In determining what makes a good estimator, there are two key features:
- The center of the sampling distribution for the estimate is the same as that of the population. When this property is true, the estimate is said to be unbiased. The most often-used measure of the center is the mean.
- The estimate has the smallest standard error when compared to other estimators. For example, in the normal distribution, the mean and median are essentially the same. However, the standard error of the median is about 1.25 times that of the standard error of the mean. We know the standard error of the mean is \(\frac{\sigma}{\sqrt{n}}\). Therefore in a normal distribution, the SE(median) is about 1.25 times \(\frac{\sigma}{\sqrt{n}}\). This is why the mean is a better estimator than the median when the data is normal (or approximately normal).
Note!
We should stop here and explain why we use the estimated standard error and not the standard error itself when constructing a confidence interval. The answer is because, typically, the population values are not known. Take, for example, the standard error of the sample proportion. It is...
\(\sqrt{\dfrac{p(1-p)}{n}}\)
If the goal is to estimate \(p\) and \(p\) is unknown, we would also then have to estimate the standard error. In this case the estimated standard error is...
\(\sqrt{\dfrac{\hat{p}(1-\hat{p})}{n}}\)
For the case for estimating the population mean, the population standard deviation, \(\sigma\), may also be unknown. When it is unknown, we can estimate it with the sample standard deviation, s. Then the estimated standard error of the sample mean is...
\(\dfrac{s}{\sqrt{n}}\)
General Format of a Confidence Interval
In putting the two properties above together, the center of our interval should be the point estimate for the parameter of interest. With the estimated standard error of the point estimate, we can include a measure of confidence to our estimate by forming a margin of error.
This you may have readily seen whenever you have heard or read a sample survey result (e.g. a survey of the current approval rating of the President, or attitude citizens have on some new policy). In such surveys, you may hear reference to the "44% of those surveyed approved of the President's reaction" (this is the sample proportion), and "the survey had a 3.5% margin or error, or ± 3.5%." This latter number is the margin of error.
With the point estimate and the margin of error, we have an interval for which the group conducting the survey is confident the parameter value falls (i.e. the proportion of U.S. citizens who approve of the President's reaction). In this example, that interval would be from 40.5% to 47.5%.
This example provides the general construction of a confidence interval:
- General form of a confidence interval
- \(sample\ statistic \pm margin\ of\ error\)
The margin of error will consist of two pieces. One is the standard error of the sample statistic. The other is some multiplier, \(M\), of this standard error, based on how confident we want to be in our estimate. This multiplier will come from the same distribution as the sampling distribution of the point estimate; for example, as we will see with the sample proportion this multiplier will come from the standard normal distribution. The general form of the margin of error is shown below.
- General form of the margin of error
- \(\text{Margin of error}=M\times \hat{SE}(\text{estimate})\)
-
*the multiplier, \(M\), depends on our level of confidence
Interpretation of a Confidence Interval
The interpretation of a confidence interval has the basic template of: "We are 'some level of percent confident' that the 'population of interest' is from 'lower bound to upper bound'. The phrases in single quotes are replaced with the specific language of the problem. We will discuss more about the interpretation of a confidence interval after we provide a few more examples.
Note!
Some might say, "Why not just be 100% confident?", but that does not make practical sense. For instance, what value comes from me saying I am 100% confident that the approval rating for the President is from 0% to 100%. That is the only interval in which one can be truly confident will capture the actual proportion. Similarly, if you were to ask your professor what they think your score will be on an exam and they reply, "zero to one hundred", what would you think of that answer?
However, one does want to be as confident as reasonably possible. Most confidence levels use ranges from 90% confidence to 99% confidence, with 95% being the most widely used. In fact, when you read a report that includes a margin of error, you can usually assume this has a 95% confidence attached to it unless otherwise stated.
Moving forward...
We're going to begin exploring confidence intervals for one population proportions. The important issue of determining the required sample size to estimate a population proportion will also be discussed in detail in this lesson.
5.3 - Inference for the Population Proportion
5.3 - Inference for the Population ProportionEarlier in the lesson, we talked about two types of estimation, point, and interval. Let's now apply them to estimate a population proportion from sample data.
Point Estimate for the Population Proportion
The point estimate of the population proportion, \(p\), is:
Point Estimate of the Population Proportion
\(\hat{p}=\dfrac{\text{# of successes in the sample}}{\text{sample size, n}}\)
From our previous lesson on sampling distributions, we know the sampling distribution of the sample proportion under certain conditions. We can use this information to construct a confidence interval for the population proportion.
Confidence Interval for the Population Proportion
Recall that:
If \(np\) and \(n(1-p)\) are greater than five, then \(\hat{p}\) is approximately normal with mean, \(p\), standard error \(\sqrt{\frac{p(1-p)}{n}}\).
Under these conditions, the sampling distribution of the sample proportion, \(\hat{p}\), is approximately Normal. The multiplier used in the confidence interval will come from the Standard Normal distribution.
5.3.1 - Construct and Interpret the CI
5.3.1 - Construct and Interpret the CIConstructing a Confidence Interval for the Population Proportion
To construct a confidence interval we're going to use the following 3 steps:
- CHECK CONDITIONS
Check all conditions before using the sampling distribution of the sample proportion.
We previously used \(np\) and \(n(1-p)\). But \(p\) is not known. Therefore, for the confidence interval, we will use
- \(n\hat{p}>5\) and
- \(n(1-\hat{p})>5\)
What can one do if the conditions are NOT satisfied?
For a confidence interval for a proportion, there is a technique called exact methods. These methods can be used if the software offers it. These exact methods are more complicated and are based on the relationship between the binomial and another distribution we will later learn called the F-distribution. The Z-method is much simpler and fairly easy to compute. In fact if you ever come across a published random survey (e.g. a Gallup poll) you can use the methods in this lesson to construct a reliable proportion confidence interval rather quickly. - CONSTRUCT THE GENERAL FORM
The general form of the confidence interval is '\(\text{point estimate }\pm M\times \hat{SE}(\text{estimate})\).' The point estimate is the sample proportion, \(\hat{p}\), and the estimated standard error is \(\hat{SE}(\hat{p})=\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\). If the conditions are satisfied, then the sampling distribution is approximately normal. Therefore, the multiplier comes from the normal distribution. This interval is also known as the one-sample z-interval for \(p\), or the Normal Approximation confidence interval for \(p\).
- \(\boldsymbol{\left(1-\alpha \right) 100\%}\) confidence interval for the population proportion, \(\boldsymbol{p}\)
- \(\hat{p}\pm z_{\alpha/2}\sqrt{\dfrac{\hat{p}(1-\hat{p})}{n}}\)
- where \(z_{\alpha/2}\) represents a z-value with \(\alpha/2\) area to the right of it.
General notes about the confidence interval...
- The \(\pm\) in the formula above means "plus or minus". It is a shorthand way of writing
\((\hat{p}-z_{\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}, \hat{p}+z_{\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}})\)
- It is centered at the point estimate, \(\hat{p}\).
- The width of the interval is determined by the margin of error.
- You must determine the multiplier.
- INTERPRET THE CONFIDENCE INTERVAL
Applying the template from earlier in the lesson we can say we are \((1-\alpha)100\%\) confident that the population proportion is between \(\hat{p}-z_{\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\) and \(\hat{p}+z_{\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\). The examples will go into more detail regarding the interpretation of the confidence interval.
Derivation of the Confidence Interval
To calculate the confidence interval, we need to know how to find the z-multiplier. So where does this \(z_{\alpha}\) come from?
The confidence interval can be derived from the following fact:
\begin{align} P\left(\left|\frac{\hat{p}-p}{\sqrt{\dfrac{\hat{p}(1-\hat{p})}{n}}}\right|\le z_{\alpha/2}\right)=1-\alpha \\ P\left(-z_{\alpha/2}\le \dfrac{\hat{p}-p}{\sqrt{\dfrac{\hat{p}(1-\hat{p})}{n}}}\le z_{\alpha/2}\right)=1-\alpha \\ P\left(\hat{p}-z_{\alpha/2}\sqrt{\dfrac{\hat{p}(1-\hat{p})}{n}}\le p \le \hat{p}+z_{\alpha/2}\sqrt{\dfrac{\hat{p}(1-\hat{p})}{n}}\right)=1-\alpha \end{align}
The figure shows the general confidence interval on the normal curve.
How to find the multiplier using the Standard Normal Distribution
\(z_a\) is the z-value having a tail area of \(a\) to its right. With some calculation, one can use the Standard Normal Cumulative Probability Table to find the value.
Example 5-1: Finding \(\boldsymbol{z_a}\)
Find using the standard Normal table: \(z_{0.15}\)
Answer
\(z_{0.15}\) means \(P(Z>z_{0.15})=0.15\). This implies that \(P(Z\le z_{0.15})=0.85\). The value from the table is 1.04.
For more detailed directions on reading the z-table or using Minitab refer to the examples on this page: 3.3.2 The Standard Normal Distribution.
Try it!
Use the Standard Normal Table to find the following:
Commonly Used Alpha Levels
The table is a list of frequently used alphas and their \(z_{\alpha/2}\) multipliers.
| Confidence Level | \(\boldsymbol{\alpha}\) | \(\boldsymbol{z_{\alpha/2}}\) | \(\boldsymbol{z_{\alpha/2}}\) Multiplier |
|---|---|---|---|
| 90% | .10 | \(z_{0.05}\) | 1.645 |
| 95% | .05 | \(z_{0.025}\) | 1.960 |
| 98% | .02 | \(z_{0.01}\) | 2.326 |
| 99% | .01 | \(z_{0.005}\) | 2.576 |
The value of the multiplier increases as the confidence level increases. This leads to wider intervals for higher confidence levels. We are more confident of catching the population value when we use a wider interval.
Example 5-2: Alpha Levels
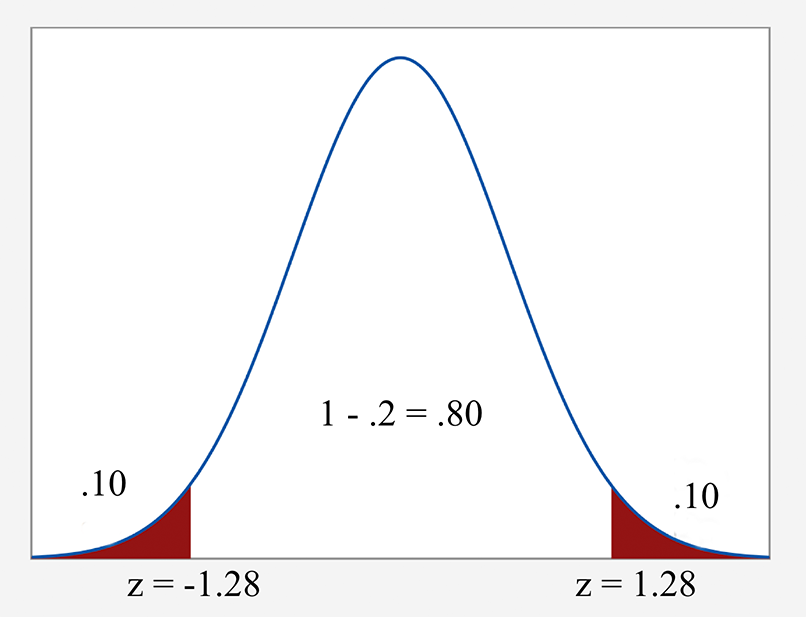
For an 80% confidence interval find \(\alpha\), \(\alpha/2\), and \(z_{\alpha/2}\).
Answer
Recall that \(\alpha\) is used to find the confidence level by taking (1 - \(\alpha)*100%\).
So for an 80% confidence we would take...
\( (1 - \alpha)*100 = 80 \) or...
\((1 - \alpha) = .8\)
\( \alpha = .2\)
Therefore, \(\alpha/2 = .2/2 = .1\)
We would have \(z_{0.10}\) which means \(P(Z>z_{0.10})=0.10\).
This implies that \(P(Z\le z_{0.10})=0.90\). The value from the table is 1.28.
Visually, you can see how these numbers relate to the normal distribution in the graph below.
Example 5-3: Approval Ratings
 A random sample of 1500 U.S. adults is taken. They are asked whether they approve or disapprove of the current president's performance so far (i.e. an approval rating). Of the 1500 surveyed, 660 respond with "approve". Calculate a 95% confidence interval for the overall approval rating of the the president.
A random sample of 1500 U.S. adults is taken. They are asked whether they approve or disapprove of the current president's performance so far (i.e. an approval rating). Of the 1500 surveyed, 660 respond with "approve". Calculate a 95% confidence interval for the overall approval rating of the the president.
Answer
Since we're dealing with a single proportion, we will examine the number of "successes" and the number of "failures". In this example there were 660 successes and 840 failures. With both successes and failures being at least 5, the condition to use the z-method to calculate the interval is acceptable.
For 95% confidence, the alpha value is 5% or 0.05 The multiplier would be a z-value with \(\alpha/2\), or 0.025 area to the right of it. Examining the standard normal table, we find that this corresponds to a z-value of 1.96.
Important Note: Many students tend to use the multiplier of 2 instead of 1.96 due to the empirical rule. As a general rule, it is always best to use the exact values rather than the rounded value.
In this example, we have a sample proportion, \(\hat{p}\), of 660/1500 = 0.44 and a sample size, \(n\), of 1500.\begin{align} \hat{p}& \pm z_{\alpha/2}\sqrt{\dfrac{\hat{p}(1-\hat{p}}{n}} &&\text{(General Form)} \\0.44 &\pm 1.96 \sqrt{\dfrac{0.44(1-0.44)}{1500}} &&\text{(Plug in the numbers)} \\ 0.44 &\pm 0.025 &&\text{(Simplify)}\end{align}
"We are 95% confident that the overall U.S. adult approval rating for the current president is from 41.5% to 46.5%." You could also see this written as, "The current U.S. approval rating for the president is 44% with a 95% margin of error of 2.5%." Commonly, the standard level of confidence is 95% so that reference is often left out as that is the assumed level of confidence unless otherwise stated. Also, the method calculates a proportion but often the reported values are converted to percentages. If you use the decimal formal (e.g. 0.415 and 0.465) then reference these as proportion and not percentage.
View the video explanation from Dr. Bulathsinhala
- In Minitab choose Stat > Basic Statistics > 1 proportion .
- From the drop down box select the Summarized data option button. (If you have the raw data you would use the default drop down of One or more samples, each in a column.)
- Enter the number of successes in the Number of Events text box, and the sample size in the Number of Trials text box.
- Choose the Options button. The default confidence level is 95. If your desire another confidence level edit appropriately.
- To use the z- interval method choose Normal Approximation from the Method text box. The exact interval is always appropriate and is the default. Under the conditions that: $n \hat{p} \ge 5, n(1− \hat{p}) \ge 5$, one can also use the z-interval to approximate the answers. The exact interval and the z-interval should be very similar when the conditions are satisfied.
- Choose OK and OK again.
Using Minitab: Approval Ratings Example
We will now use Minitab to verify our by-hand results. Recall in that example a random sample of 1500 was taken from the population of U.S. adults, with 660 responding with a positive approval.
Answer
In Minitab and following the steps above, we would enter 660 for the Number of Events and 1500 for the Number of Trials. The confidence level was 95% and we satisfied the necessary conditions to use the Normal Approximation (or z-interval) method. The results are:
Test and CI for One Proportion
| Sample | X | N | Sample p | 95% CI |
|---|---|---|---|---|
| 1 | 660 | 1500 | 0.440000 | (0.414880, 0.465120) |
Using the normal approximation.
These results closely match our by-hand interval of 0.415 to 0.465
What if we had calculated the exact confidence interval (i.e. did not choose Normal Approximation as the method)? With the exact method the interval is (0.414685, 0.465550). Consistent to three decimal places in this case. You will notice that in the output Minitab does provide a notification that the normal approximation was used.
We want to know the proportion of graduate students at Penn State who are Democrats. To answer the question, we give out the following survey:
Are you a Democrat? Please circle one answer.
- Yes
- No
Suppose that we get 10 people that circled Yes and 20 people that circled No (that includes the case when people don't know whether they are Democrats!!)
- Let X = the number of successes (number of students who chose Yes) = 10
- n = number of trials = 30
Find a 90% confidence interval for the proportion of graduate students who are democrats.
You should first check the conditions. We know \(\hat{p}=\frac{10}{30}=0.333\) and \(n=30\) Therefore, \(n\hat{p}=30(0.333)=10\) and \(n(1-\hat{p})=20\). Since both values are greater than 5, we can use the Normal distribution.
The z multiplier will be \(z_{0.1/2}=1.645\)
\(\hat{p}\pm 1.645\sqrt{\dfrac{\hat{p}(1-\hat{p})}{n}}=0.333\pm 1.645\sqrt{\dfrac{0.333(1-0.333)}{30}}=0.333\pm0.1415=(0.1915, 0.4745)\).
We are 90% confident that the population proportion of graduate students at Penn State who are democrats is between 19.15% and 47.45%.
The video demonstrates this same example using Minitab.
5.3.2 - Interpreting the CI
5.3.2 - Interpreting the CIMore on the Interpretation of a Confidence Interval
In the graph below, we show 10 replications (for each replication, we sample 30 students and ask them whether they are Democrats) and compute an 80% Confidence Interval each time. We are lucky in this set of 10 replications and get exactly 8 out of 10 intervals that contain the parameter. Due to the small number of replications (only 10), it is quite possible that we get 9 out of 10 or 7 out of 10 that contain the true parameter. On the other hand, if we try it 10,000 (a large number of) times, the percentage that contains the true proportions will be very close to 80%.
If we repeatedly draw random samples of size n from the population where the proportion of success in the population is $p$ and calculate the confidence interval each time, we would expect that $100(1 - \alpha)$% of the intervals would contain the true parameter, $p$.
5.3.3 - Sample Size Computation
5.3.3 - Sample Size ComputationSample Size Computation for the Population Proportion Confidence Interval
An important part of obtaining desired results is to get a large enough sample size. We can use what we know about the margin of error and the desired level of confidence to determine an appropriate sample size.
Recall that the margin of error, E, is half of the width of the confidence interval. Therefore for a one sample proportion,
\(E=z_{\alpha/2}\sqrt{\dfrac{\hat{p}(1-\hat{p})}{n}}\)
- Precision
- The wider the interval, the poorer the precision. Note that the higher the confidence level, the wider the width (or equivalently, half width) of the interval and thus the poorer the precision.
Since the confidence level reflects the success rate of the method we use to get the confidence interval, we like to have a narrower interval while keeping the confidence level at a reasonably higher level.
For most newspapers and magazine polls, it is understood that the margin of error is calculated for a 95% confidence interval (if not stated otherwise). A 3% margin of error is a popular choice also. For instance, you might see a television poll state that the "approval rating of the president is 72%; the margin of error of the poll is plus or minus 3%."
If we want the margin of error smaller (i.e., narrower intervals), we can increase the sample size. Or, if you calculate a 90% confidence interval instead of a 95% confidence interval, the margin of error will also be smaller. However, when one reports it, remember to state that the confidence interval is only 90% because otherwise, people will assume 95% confidence.
Determining the Required Sample Size
If the desired margin of error E is specified and the desired confidence level is specified, the required sample size to meet the requirements can be calculated by two methods:
- Educated Guess
- \(n=\dfrac{z^2_{\alpha/2}\hat{p}_g(1-\hat{p}_g)}{E^2}\)
Where \(\hat{p}_g\) is an educated guess for the parameter \(p\).
*The educated guess method is used if it is relatively inexpensive to sample more elements when needed.
- Conservative Method
- \(n=\dfrac{z^2_{\alpha/2}(\frac{1}{2})^2}{E^2}\)
- This formula can be obtained from part (a) using the fact that:
For \(0 \le p \le 1, p (1 - p)\) achieves its largest value at \(p=\frac{1}{2}\).
*The conservative method is used if the start-up cost of sampling is expensive and thus it is not economical to sample more elements later.
The sample size obtained from using the educated guess is usually smaller than the one obtained using the conservative method. This smaller sample size means there is some risk that the resulting confidence interval may be wider than desired. Using the sample size by the conservative method has no such risk.
Example 5-4
Suppose a television poll states that the "approval rating of the president is 72%." For the next poll of the president's approval rating, we want to get a margin of error of 1% with 95% confidence. How many individuals should we sample?
Answer
Educated Guess:
\(z_{0.025} = 1.96, E = 0.01\)
Therefore,
\(n=\dfrac{(1.96)^2(0.72)(1-0.72)}{(0.01)^2}=7744.67\)
The sample size needed is 7745 people . We always need to round up to the next integer when the result is not a whole number. We discuss this in detail below.
Conservative Method:
\(z_{0.025} = 1.96, E = 0.01\)
Therefore,
\(n=\dfrac{(1.96)^2(0.5)(1-0.5)}{(0.01)^2}=9604\)
The sample size is 9604 people .
Cautions About Sample Size Calculations
- Why do we need to round up?
Because we are estimating the smallest sample size needed to produce the desired error. Since we cannot sample a portion of a subject (e.g. we cannot take 0.66 of a subject) we need to round up to guarantee a large enough sample.
- Remember that this is the minimum sample size needed for our study.
If we encounter a situation where the response rate is not 100% then if we just sample the calculated size, in the end, we will end up with a less than desired sample size. To counter this, we can adjust the calculated sample size by dividing by an anticipated response rate. For instance, using the above example if we expected about 40% of the those contacted to actually participate in our survey (i.e. a 40% response rate) then we would need to sample 7745/0.4=19,362.5 or 19,363. In other words, our actual sample size would need to be 19,363 given the 40% response rate.
5.4 - Inference for the Population Mean
5.4 - Inference for the Population MeanOverview
In this section, we discuss how to find confidence intervals for the population mean. The idea and interpretation of the confidence interval will be similar to that of the population proportion only applied to the population mean, \(\mu\).
We start with the case where the population standard deviation, \(\sigma\), is known. We continue to the more realistic case where \(\sigma\) is not known. For the latter case, we need to recall the \(t\)-distribution. We end this section by presenting how to determine a sample size for a desired margin of error and confidence.
Point Estimates for a Population Mean
The point estimate of the population mean, \(\mu\) is:
- Point Estimate of the Population Mean
- \(\bar{x}=\) sample mean
If one wants to know how accurate the sample mean is to estimate the population mean, we need some probability statement. We will want to know the sampling distribution of \(\bar{x}\). From this distribution, we can get a confidence interval. Such an interval provides a range of values for which the parameter value is believed to fall. An interval is more likely to be "correct" than a point estimate.
5.4.1 - Construct and Interpret the CI
5.4.1 - Construct and Interpret the CIConstructing a Confidence Interval for the Population Mean
To construct a confidence interval for a population mean, we're going to apply the same three steps as with the population proportion, but first, let's look at the two possible cases.
Case 1: $\sigma$ is known
In the previous lesson, we learned that if the population is normal with mean \(\mu\) and standard deviation, \(\sigma\), then the distribution of the sample mean will be Normal with mean \(\mu\) and standard error \(\frac{\sigma}{\sqrt{n}}\).
Following the similar idea to developing the confidence interval for \(p\), the \((1-\alpha)\)100% confidence interval for the population mean \(\mu\) is...
\(P\left(\left|\dfrac{\bar{x}-\mu}{\dfrac{\sigma}{\sqrt{n}}}\right|\le z_{\alpha/2}\right)=1-\alpha\)
A little bit of algebra will lead you to...
\(P\left(\bar{x}-z_{\alpha/2}\dfrac{\sigma}{\sqrt{n}}\le \mu\le \bar{x}+z_{\alpha/2}\dfrac{\sigma}{\sqrt{n}}\right)=1-\alpha\)
In other words, the \((1-\alpha)\)100% confidence interval for \(\mu\) is:
\(\bar{x}\pm z_{\alpha/2}\dfrac{\sigma}{\sqrt{n}}\)
Notice for this case, the only condition we need is the population distribution to be normal.
Note!
The case where \(\sigma\) is known is unrealistic. We explain it here briefly because it reinforces what we have previously learned. We do not present examples in this case.Case 2: \(\sigma\) is unknown
When the population is normal or when the sample size is large then,
\(Z=\dfrac{\bar{x}-\mu}{\dfrac{\sigma}{\sqrt{n}}}\)
where Z has a standard Normal distribution.
Usually, we don't know \(\sigma\), so what can we do?
Recall that if X comes from a normal distribution with mean, $\mu$, and variance, $\sigma^2$, or if $n\ge 30$, then the sampling distribution will be approximately normal with mean $\mu$ and standard error, \(SE(\bar{X})=\frac{\sigma}{\sqrt{n}}\)
One way to estimate \(\sigma\) is by \(s\), the standard deviation of the sample, and replace \(\sigma\) by \(s\) in the above Z-equation. However, this new quotient no longer has a Z-distribution. Instead it has a t-distribution. We call the following a 'studentized' version of \(\bar{X}\):
\(t=\dfrac{\bar{X}-\mu}{\dfrac{s}{\sqrt{n}}}\)
Constructing the Confidence Interval
-
CHECK THE CONDITIONS
One of the following conditions need to be satisfied:
- If the sample comes from a Normal distribution, then the sample mean will also be normal. In this case, \(\dfrac{\bar{x}-\mu}{\frac{s}{\sqrt{n}}}\) will follow a \(t\)-distribution with \(n-1\) degrees of freedom.
- If the sample does not come from a normal distribution but the sample size is large (\(n\ge 30\)), we can apply the Central Limit Theorem and state that \(\bar{X}\) is approximately normal. Therefore, \(\dfrac{\bar{x}-\mu}{\frac{s}{\sqrt{n}}}\) will follow a \(t\)-distribution with \(n-1\) degrees of freedom.
-
CONSTRUCT THE GENERAL FORM
- \((1-\alpha)\)100% Confidence Interval for the Population Mean, \(\mu\)
- \(\bar{x}\pm t_{\alpha/2}\dfrac{s}{\sqrt{n}}\)
where the t-distribution has \(df = n - 1\). This interval is also known as the one-sample t-interval for the population mean.
-
INTERPRET THE CONFIDENCE INTERVAL
We are \((1-\alpha)100\%\) confident that the population mean, \(\mu\), is between \(\bar{x}-t_{\alpha/2}\frac{s}{\sqrt{n}}\) and \(\bar{x}+t_{\alpha/2}\frac{s}{\sqrt{n}}\).
What if the conditions are not met?
What will you do if you cannot use the t-interval? What do we do when the above conditions are not satisfied?
- If you do not know if the distribution comes from a normally distributed population and the sample size is small (i.e \(n<30\)), you can use the Normal Probability Plot to check if the data come from a normal distribution.
- You may want to consider what is known as nonparametric statistical methods. A procedure such as the one-sample Wilcoxon procedure. Lesson 11 introduces nonparametric statistical methods.
5.4.2 - The t-distribution
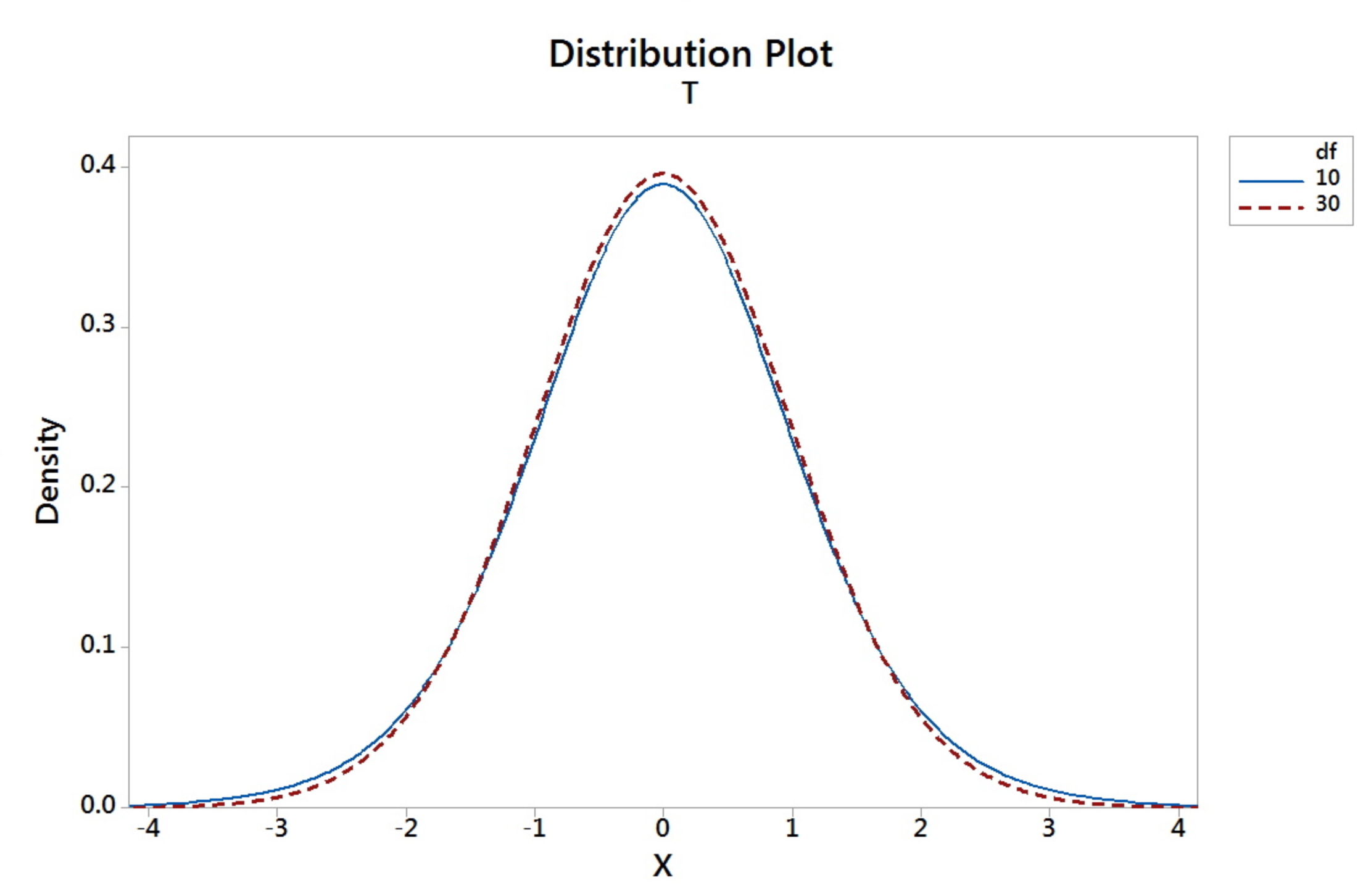
5.4.2 - The t-distributionIn 1908, William Sealy Gosset from Guinness Breweries discovered the t-distribution. His pen-name was Student and thus it is called the "Student's t-distribution."
The t-distribution is different for different sample size, n. Thus, tables, as detailed as the standard normal table, are not provided in the usual statistics books. The graph below shows the t-distribution for degrees of freedom of 10 (blue) and 30 (red dashed).
Properties of the t-distribution
- t is symmetric about 0
- t-distribution is more variable than the Standard Normal distribution
- t-distributions are different for different degrees of freedom (d.f.).
- The larger $n$ gets (or as $n$ goes to infinity), the closer the $t$-distribution is to the $z$.
- The meaning of $t_\alpha$ is the $t$-value having the area "$\alpha$" to the right of it.
Example 5-5: Finding t-values
Use this t-table or the one in your text to find following the example.
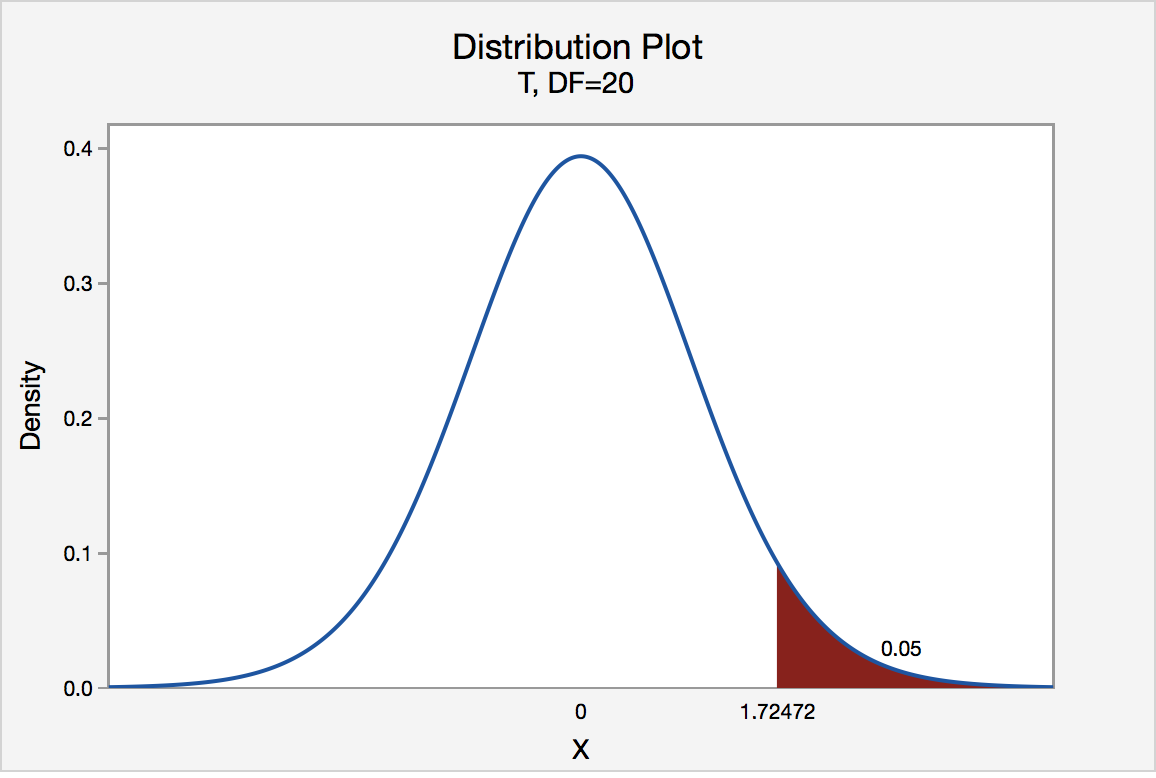
Find \(t_{0.05}\) where the degree of freedom is 20.
In a t-distribution table below the top row represents the upper tail area, while the first column are the degrees of freedom.
The \(t_{0.05}\) where the degree of freedom is 20 is 1.725 .
| df | 0.40 | 0.25 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 | .0005 |
|---|---|---|---|---|---|---|---|---|---|
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 18 | 0.257 | 0.688 | 1.330 | 1.734 | 2.101 | 2.552 | 2.878 | 3.610 | 3.922 |
| 19 | 0.257 | 0.688 | 1.328 | 1.729 | 2.093 | 2.539 | 2.861 | 3.579 | 3.883 |
| 20 | 0.257 | 0.687 | 1.325 | 1.725 | 2.086 | 2.528 | 2.845 | 3.552 | 3.850 |
| 21 | 0.257 | 0.686 | 1.323 | 1.721 | 2.080 | 2.518 | 2.831 | 3.527 | 3.819 |
The graph shows that the \(\alpha\) values at the top of this table are the upper tail areas of the distribution.
Find \(t_{0.05}\) where the degree of freedom is 34.
What do we do when the degrees of freedom are not on the table? The t-table degrees of freedom run continuously from 1 to 30, then go by intervals after 30 (e.g. after 30 we have 35). In such cases, we can use software such as Minitab to find a more exact value for the multiplier as opposed to using a degrees of freedom that is "close".
To find the t-value in Minitab...
- From the Minitab Menu select Calc > Probability Distributions > t...
- Choose inverse cumulative probability
- Enter the degrees of freedom
- Set the input constant as 0.95 (1 - 0.05).
- Choose OK
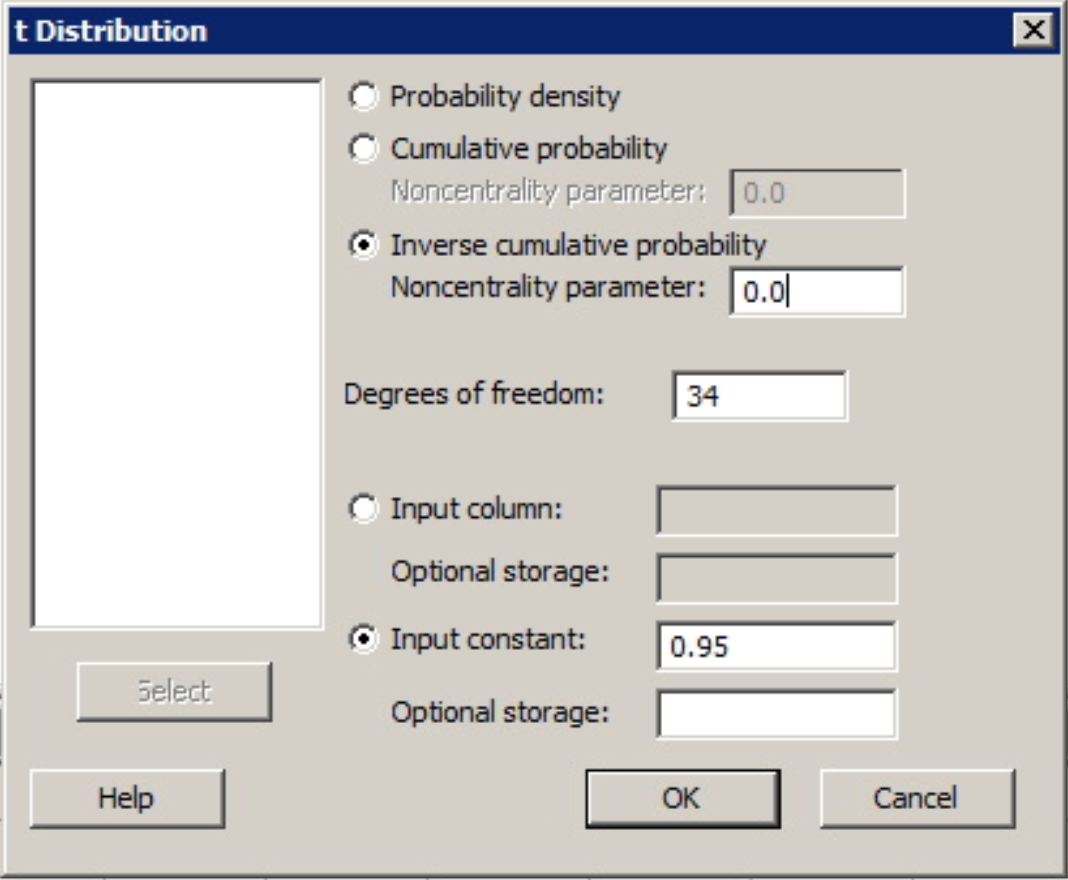
The output from Minitab gives us \(t_{0.05}\) with df= 34 as 1.69092.
| P (X \(\le\) x) | x |
|---|---|
| 0.95 | 1.69092 |
The t-value for an \(\alpha\) of .05 and df of 30 is 1.697.
| df | 0.40 | 0.25 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 | .0005 |
|---|---|---|---|---|---|---|---|---|---|
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 27 | 0.256 | 0.684 | 1.314 | 1.703 | 2.052 | 2.473 | 2.771 | 3.421 | 3.690 |
| 28 | 0.256 | 0.683 | 1.313 | 1.701 | 2.048 | 2.467 | 2.763 | 3.408 | 3.674 |
| 29 | 0.256 | 0.683 | 1.311 | 1.699 | 2.045 | 2.462 | 2.756 | 3.396 | 3.659 |
| 30 | 0.256 | 0.683 | 1.310 | 1.697 | 2.042 | 2.457 | 2.750 | 3.385 | 3.646 |
Note! When the sample size is larger than 30, the t-values are not that different from the z-values. Thus, a crude estimate for \(t_{0.05}\) with 34 degrees of freedom is \(z_{0.05} = 1.645\). Although it is a crude estimate, when software is available, it is best to find the $t$ values rather than use the $z$.
5.4.3 - Example
5.4.3 - ExampleExample 5-6: Emergency Room Wait Time

You are interested in the average emergency room (ER) wait time at your local hospital. You take a random sample of 50 patients who visit the ER over the past week. From this sample, the mean wait time was 30 minutes and the standard deviation was 20 minutes. Find a 95% confidence interval for the average ER wait time for the hospital.
Answer
Note that, \(t_{0.025,49}\approx z_{0.025}\) as the degrees of freedom is 49
- In Minitab choose Stat > Basic Statistics > 1-Sample t .
- From the drop down box select the Summarized data option button. (If you have the raw data you would use the default drop down of One or more samples, each in a column.)
- Enter the sample size, sample mean, and sample standard deviation in their respective text boxes.
- Click the Options button. The default confidence level is 95. If your desire another confidence level edit appropriately.
- Click OK and OK again.
Using Minitab: Emergency Room Wait Time Example
Referring to our prior example of average emergency room wait time from our discussion on confidence intervals for a population mean, our by-hand calculations produced a 95% confidence interval of 24.28 to 35.72 minutes. Recall the following for that example: sample size 50, sample mean 30, and sample standard deviation 20.
In Minitab following the above steps, we get a 95% confidence interval:
| N | Mean | StDev | SE Mean | 95% CI |
|---|---|---|---|---|
| 50 | 30.00 | 20.00 | 2.84 | (24.32, 35.68) |
The slight discrepancy between the estimates is due to our by-hand calculation using the t-value associated with 40 degrees of freedom since the table did not include a d.f. of 49. Minitab used a t-value for the actually 49 degrees of freedom. With the larger degrees of freedom comes a smaller t-value. This would result in a smaller margin of error and a narrower interval - precisely what we have here.
The mean length of certain construction lumber is supposed to be 8.5 feet. A random sample of 81 pieces of such lumber gives a sample mean of 8.3 feet and a sample standard deviation of 1.2 feet.
- Step 1: Check the conditions: The sample size is large ($n\ge 30$), so we may continue using the value from the t-distribution as our multiplier.
- Step 2: Construct the CI: The degrees of freedom are $n-1=80$. If we use the table, with d.f of 60, $t_{0.025}=2$.
The 95% confidence interval is \begin{align} &=\bar{x}\pm t_{0.025}\dfrac{s}{\sqrt{n}}\\ &=8.3\pm 2\dfrac{1.2}{\sqrt{81}}\\ &=8.3\pm 0.2667\\ &=(8.0333, 8.5667) \end{align}
- Step 1: Check the conditions: The sample size is large ($n\ge 30$), so we may continue using the value from the t-distribution as our multiplier.
- Step 2: Construct the CI: The degrees of freedom are $n-1=80$. If we use the table, with d.f of 60, $t_{0.005}=2.66$. The 99% confidence interval is \begin{align} &=\bar{x}\pm t_{0.005}\dfrac{s}{\sqrt{n}}\\ &=8.3\pm 2.66\dfrac{1.2}{\sqrt{81}}\\ &=8.3\pm 0.3547\\ &=(7.9453, 8.6547) \end{align}
Reflecting back on interpretation of a proportion interval, we see the same basic structure: level of confidence, parameter of interest, lower and upper bounds.
5.4.4 - Checking Normality
5.4.4 - Checking NormalityUsing Normal Probability Plot to Check Normality
If the sample size is less than 30, one needs to use a Normal Probability Plot to check whether the assumption that the data come from a normal distribution is valid.
- Normal Probability Plot
- The Normal Probability Plot is a graph that allows us to assess whether or not the data comes from a normal distribution.
Example 5-7: Rattlesnake Lengths
It is very time consuming to find rattlesnakes and nerve racking to measure them (for obvious reasons). A scientist randomly finds 12 snakes from the central Pennsylvania area and measures their length. The following twelve measurements in inches are obtained:
40.2, 43.1, 45.5, 44.5, 39.5, 38.5, 40.2, 41.0, 41.6, 43.1, 44.9, 42.8
Using the above data, find a 90% confidence interval for the mean length of rattlesnakes in the central Pennsylvania area.
Step 1 Check Conditions
Think about what conditions you need to check. The sample size is only 12. The scenario does not give us an indication that the lengths follow a normal distribution. Therefore, let's do a normal probability plot to check whether the assumption that the data come from a normal distribution is valid.
Minitab: Creating a normal probability plot
To create a normal probability plot in Minitab:
- Enter the 12 measurements into one column (name it length for this example) or upload the snakes.txt file.
- Type or upload the data in the first column in Minitab.
- Choose Graph > Probability Plot
Here is the normal probability plot for the rattlesnake data. What do you conclude about whether they may come from a normal distribution?
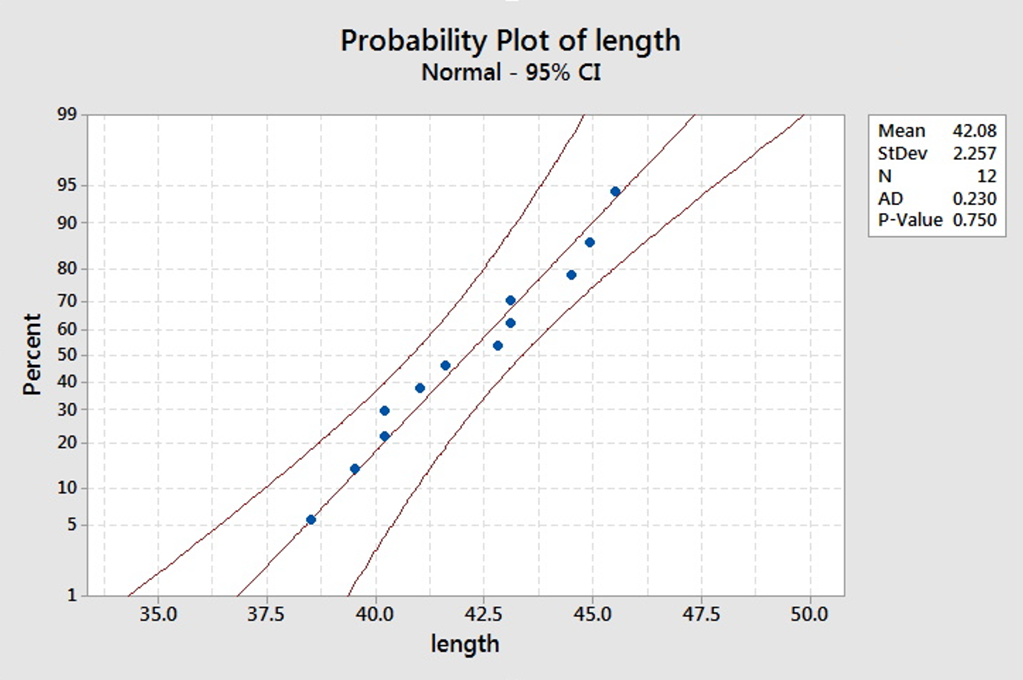
Since the points all fall within the confidence limits, it is reasonable to suggest that the data come from a normal distribution.
Step 2 Construct the CI
Now, we can proceed to find the 90% t-interval for the mean length of rattlesnakes in the central Pennsylvania area since even though the sample size is less than 30, the normality plot shows that the data may come from a normal distribution.
Minitab: Find the t-interval using Minitab
- Enter the 12 measurements into one column (name it length for this example)
- Choose Stat > Basic Statistics > 1-Sample t
- Click on the variable (length for this example) and change to the desired confidence level
The Minitab output will provide the confidence interval. We get the following:
| N | Mean | StDev | SE Mean | 90% CI |
|---|---|---|---|---|
| 12 | 42.075 | 2.257 | 0.652 | (40.905, 43.245) |
View the video to see these steps within Minitab.
Video: Minitab: 90% Confidence Interval for Continuous Data in Minitab
Step 3 Interpret the Interval
We are 90% confident that the population mean lengths of rattlesnakes is between 40.905 and 43.245 inches.
5.4.5 - Sample Size Computation
5.4.5 - Sample Size ComputationSample Size Computation for the Population Mean Confidence Interval
Recall that a \((1-\alpha)\)100% confidence interval for \(\mu\) is \(\bar{x}\pm t_{\alpha/2}\dfrac{s}{\sqrt{n}}\) where the multiplier \(t\) has a t-distribution with \(df = n - 1\). Thus, the margin of error, E, is equal to:
\(E=t_{\alpha/2}\dfrac{s}{\sqrt{n}}\)
To determine the sample size, one first decides the confidence level and the half width of the interval one wants. Then we can find the sample size to yield an interval with that confidence level and with a half width not more than the specified one. The crude method to find the sample size: \(n=\left(\dfrac{z_{\alpha/2}\sigma}{E}\right)^2\) Then round up to the next whole integer.
Example 5-8: Spring Break
A marketing research firm wants to estimate the average amount a student spends during the Spring break. They want to determine it to within \$120 with 90% confidence. One can roughly say that it ranges from \$100 to \$1700. How many students should they sample?
Answer
To use the formula, we need all the pieces for \(n=\left(\dfrac{z_{\alpha/2}\sigma}{E}\right)^2\). We know that \(z_{\alpha/2}=1.645\) (for 90%). The margin of error, \(E\), is 120. The only piece missing is \(\sigma\). Since the standard deviation is not given in the problem, we can estimate it using \(\dfrac{\text{range}}{4}\) from Lesson 1. Therefore, \(\sigma=\dfrac{1700-100}{4}=400\). So we have...
\begin{align} n &=\left(\dfrac{1.645(400)}{120}\right)^2\\ &=30.07 \end{align}
Therefore, a sample of size \(n=31\) is required.
Note! In homework and exams, it is fine if you simply use the cruder method. A more accurate method is provided in the following for your reference only.
The Iterative Method
A more accurate method to estimate the sample size: iteratively evaluate the formula since the t value also depends on n.
\(n=\left(\dfrac{t_{\alpha/2}s}{E}\right)^2\)
Use the example above for illustration. Start with an initial guess for $n$, plug in the formula, and iteratively solve for \(n\).
If the initial guess for \(n\) is 20, \(t_{0.05} = 1.729\) and degrees of freedom = 19,
\(n=\left(\dfrac{t_{\alpha/2}s}{E}\right)^2=n=\left(\dfrac{1.729(400)}{120}\right)^2=33.21\)
For \(n = 34\), degree of freedom = 33, and \(t_{0.05} = 1.697\)
\(n=\left(\dfrac{t_{\alpha/2}s}{E}\right)^2=n=\left(\dfrac{1.697(400)}{120}\right)^2=31.99\)
If we use \(n = 32\), the result is the same. Thus, the more accurate answer to the example is to sample 32 students.
5.5 - Lesson 5 Summary
5.5 - Lesson 5 SummaryIn this Lesson, we learned how to apply sampling distribution theory to find confidence intervals for the population mean and the population proportion.
We discussed the important steps required to find confidence intervals.
- Step 1: Check the Conditions or Assumptions
- Step 2: Construct the Confidence Interval
- Step 3: Interpret the CI.
In the next lesson, we will present hypothesis testing and learn how hypothesis tests are related to confidence intervals.