Lesson 9: Linear Regression Foundations
Lesson 9: Linear Regression FoundationsOverview
In this Lesson, we will first introduce the Simple Linear Regression (SLR) Model and the Correlation Coefficient. Inferences for the simple linear regression model will be discussed, and the critical distinction between inference for mean response and inference for the outcome will be clarified. We will also introduce a basic understanding of the multiple regression model.
Regression analysis is a tool to investigate how two or more variables are related. Quite often we want to see how a specific variable of interest is affected by one or more variables. For example, one may wish to use a person's height, gender, race, etc. to predict a person's weight. Let us first consider the simplest case: using a person's height to predict the person's weight.
Example: Estimating Weights
If you are asked to estimate the weight of a STAT 500 student, what will you use as a point estimate? If I tell you that the height of the student is 70 inches, can you give a better estimate of the person's weight?
Answer
For the first part, the point estimate would be the average weight (or the median weight) of a STAT 500 student. If you know the student is 70 inches, then, yes, you can give a better estimate of the person’s weight, but only if you have some idea about how height and weight are related.
It is important to distinguish between the variable of interest and the variable(s) we will use to predict the variable of interest.
- Response Variable
- Denoted, Y, is also called the variable of interest or dependent variable. In the example, weight is the response variable.
- Predictor Variable
- Denoted, X, is also called the explanatory variable or independent variable. In the example, height is the predictor.
When there is only one predictor variable, we refer to the regression model as a simple linear regression model.
To use known information to provide a better estimate, we need to understand how the dependent and independent variables are related.
In statistics, we can describe how variables are related using a mathematical function. The function along with other assumptions is called a model. There are many models we can consider. In this class, we will focus on linear models, particularly, when there is only one predictor variable. We refer to this model as the simple linear regression model.
Objectives
- Use plots and summary statistics to describe the relationship between the response variable and the predictor variable.
- Perform a hypothesis test for the population correlation.
- Find the regression equation and interpret the results.
- Apply the regression model and know the limitations.
- Find an interval estimate for the population slope and interpret the interval.
9.1 - Linear Relationships
9.1 - Linear RelationshipsTo define a useful model, we must investigate the relationship between the response and the predictor variables. As mentioned before, the focus of this Lesson is linear relationships.
For a brief review of linear functions, recall that the equation of a line has the following form:
\(y=mx+b\)
where m is the slope and b is the y-intercept.
Given two points on a line, \((x_1, y_1)\) and \((x_2, y_2)\), the slope is calculated by:
\begin{align} m&=\dfrac{y_2-y_1}{x_2-x_1}\\&=\dfrac{\text{change in y}}{\text{change in x}}\\&=\frac{\text{rise}}{\text{run}} \end{align}
The slope of a line describes a lot about the linear relationship between two variables. If the slope is positive, then there is a positive linear relationship, i.e., as one increases, the other increases. If the slope is negative, then there is a negative linear relationship, i.e., as one increases the other variable decreases. If the slope is 0, then as one increases, the other remains constant.
When we look for linear relationships between two variables, it is rarely the case where the coordinates fall exactly on a straight line; there will be some error. In the next sections, we will show how to examine the data for a linear relationship (i.e., the scatterplot) and how to find a measure to describe the linear relationship (i.e., correlation).
9.1.1 - Scatterplots
9.1.1 - ScatterplotsIf the interest is to investigate the relationship between two quantitative variables, one valuable tool is the scatterplot.
- Scatterplot
- A graphical representation of two quantitative variables where the explanatory variable is on the x-axis and the response variable is on the y-axis.
When we look at the scatterplot, keep in mind the following questions:
- What is the direction of the relationship?
- Is the relationship linear or nonlinear?
- Is the relationship weak, moderate, or strong?
- Are there any outliers or extreme values?
We describe the direction of the relationship as positive or negative. A positive relationship means that as the value of the explanatory variable increases, the value of the response variable increases, in general. A negative relationship implies that as the value of the explanatory variable increases, the value of the response variable tends to decrease.
Example 9-1: Student height and weight (Scatterplots)
Suppose we took a sample from students at a large university and asked them about their height and weight. The data can be found here university_ht_wt.txt.
The first three observations are:
|
Height (inches) |
Weight (pounds) |
|---|---|
|
72 |
200 |
|
68 |
165 |
|
69 |
160 |
We let \(X\) denote the height and \(Y\) denote the weight of the student. The observations are then considered as coordinates \((x,y)\). For example, student 1 has coordinate (72,200). These coordinates are plotted on the x-y plane.
We can use Minitab to create the scatterplot.
Minitab: Scatterplots
We can create our scatterplot in Minitab following these steps.
- Choose Graph > Scatterplot > Simple
- Choose OK
Scatterplot of Weight vs Height
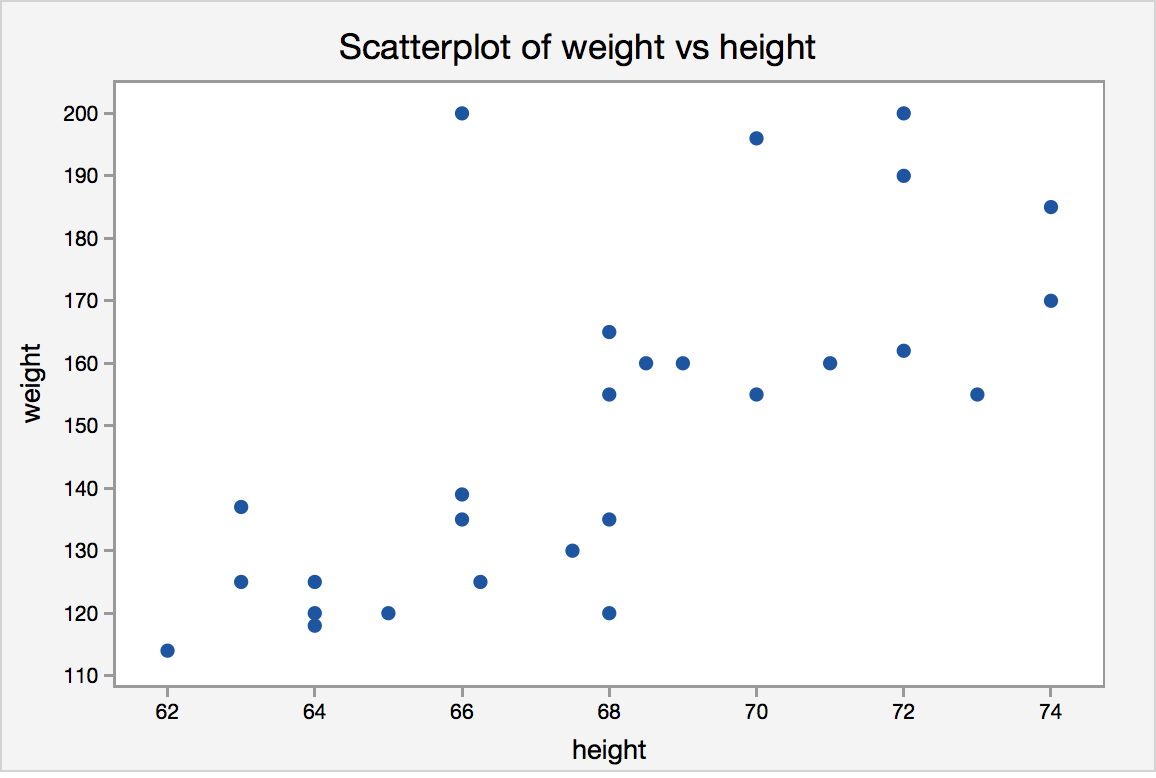
The scatterplot shows that, in general, as height increases, weight increases. We say “in general” because it is not always the case. For example, the observation with a height of 66 inches and a weight of 200 pounds does not seem to follow the trend of the data.
The two variables seem to have a positive relationship. As the height increases, weight tends to increase as well. The relationship does not seem to be perfectly linear, i.e., the points do not fall on a straight line, but it does seem to follow a straight line moderately, with some variability.
Try it!
An elementary school teacher gives her students two spelling tests a year. Each test contains 24 words, and the score is the number of words spelled correctly. The teacher is interested in the relationship between the score on the first test and the score on the second test. Using the scatterplot, comment on the relationship between the two variables.
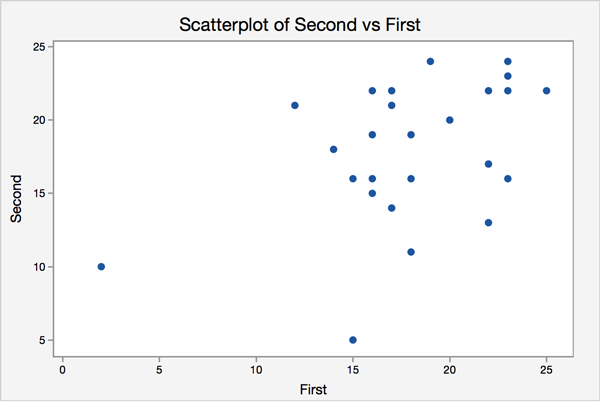
In the next section, we will introduce correlation. Correlation is a measure that gives us an idea of the strength and direction of the linear relationship between two quantitative variables.
9.1.2 - Correlation
9.1.2 - CorrelationIf we want to provide a measure of the strength of the linear relationship between two quantitative variables, a good way is to report the correlation coefficient between them.
The sample correlation coefficient is typically denoted as \(r\). It is also known as Pearson’s \(r\). The population correlation coefficient is generally denoted as \(\rho\), pronounced “rho.”
- Sample Correlation Coefficient
-
The sample correlation coefficient, \(r\), is calculated using the following formula:
\( r=\dfrac{\sum (x_i-\bar{x})(y_i-\bar{y}) }{\sqrt{\sum (x_i-\bar{x})^2}\sqrt{\sum (y_i-\bar{y})^2}} \)
Properties of the correlation coefficient, \(r\):
- \(-1\le r\le 1\), i.e. \(r\) takes values between -1 and +1, inclusive.
- The sign of the correlation provides the direction of the linear relationship. The sign indicates whether the two variables are positively or negatively related.
- A correlation of 0 means there is no linear relationship.
- There are no units attached to \(r\).
- As the magnitude of \(r\) approaches 1, the stronger the linear relationship.
- As the magnitude of \(r \) approaches 0, the weaker the linear relationship.
- If we fit the simple linear regression model between Y and X, then \(r\) has the same sign as \(\beta_1\), which is the coefficient of X in the linear regression equation. -- more on this later.
- The correlation value would be the same regardless of which variable we defined as X and Y.
Note! The correlation is unit free. We can see this easier using the equation above. Consider, for example, that we are interested in the correlation between X = height (inches) and Y = weight (pounds). In the equation above, the numerator would have the units of \(\text{pounds}^*\text{inches}\). The denominator would include taking the square root of pounds squared and inches squared, leaving us again with units of \(\text{pounds}^*\text{inches}\). Therefore the units would cancel out.
Visualizing Correlation
The following four graphs illustrate four possible situations for the values of r. Pay particular attention to graph (d) which shows a strong relationship between y and x but where r = 0. Note that no linear relationship does not imply no relationship exists!
a) \(r > 0\)
b) \(r < 0\)
c) \(r = 0\)
d) \(r=0\)
Example 9-2: Sales and Advertising (Correlation)
We have collected five months of sales and advertising dollars for a small company we own. Sales units are in thousands of dollars, and advertising units are in hundreds of dollars. Our interest is determining if a linear relationship exists between sales and advertising. The data is as follows:
| Sales (Y) | Advertising (X) |
|---|---|
| 1 | 1 |
| 1 | 2 |
| 2 | 3 |
| 2 | 4 |
| 4 | 5 |
Find the sample correlation and interpret the value.
| \(y_i-\bar{y}\) | \(x_i-\bar{x}\) | \((x_i-\bar{x})(y_i-\bar{y})\) |
|---|---|---|
| \(1-2=-1\) | \(1-3=-2\) | \((-1)(-2)=2\) |
| \(1-2=-1\) | \(2-3=-1\) | \((-1)(-1)=1\) |
| \(2-2=0\) | \(3-3=0\) | \((0)(0)=0\) |
| \(2-2=0\) | \(4-3=1\) | \((0)(1)=0\) |
| \(4-2=2\) | \(5-3=2\) | \((2)(2)=4\) |
From the table we can calculate the following sums...
\(\sum(y_i-\bar{y})^2=(-1)^2+(-1)^2+0+0+2^2=6 \;\text{(sum of first column)}\)
\(\sum(x_i-\bar{x})^2=(-2)^2+(-1)^2+0+1^2+2^2=10 \;\text{(sum of second column)}\)
\(\sum(x_i-\bar{x})(y_i-\bar{y})=2+1+0+0+4=7 \;\text{(sum of third column)}\)
Using these numbers in the formula for r...
\(r=\dfrac{\sum (x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\sum(x_i-\bar{x})^2}\sqrt{\sum(y_i-\bar{y})^2}}=\dfrac{7}{\sqrt{10}\sqrt{6}}=0.9037\)
Using Minitab to calculate r
To calculate r using Minitab:
- Open Minitab and upload the data (for this example type the Y data into a column (e.g., C1) and the X data into a column (e.g., C2))
- Choose Stat > Basic Statistics > Correlation
- Specify the response and explanatory variables in the dialog box (X and Y in this example).
Minitab output for this example:
Correlation: Y,X
Correlations
P-value
0.035
The sample correlation is 0.904. This value indicates a strong positive linear relationship between sales and advertising.
Try it!
Using the following data, calculate the correlation and interpret the value.
| X | Y |
|---|---|
| 2 | 7 |
| 4 | 11 |
| 14 | 29 |
| 13 | 28 |
| 15 | 32 |
The mean of \(X\) is 9.6 and the mean of \(Y\) is 21.4. The sums are...
\(\sum (x_i-\bar{x})^2=149.2\)
\(\sum (y_i-\bar{y})^2=529.2\)
\(\sum (x_i-\bar{x})(y_i-\bar{y})=280.8\)
Using these sums in the formula for r...
\(r=\dfrac{\sum(x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\sum(x_i-\bar{x})^2}\sqrt{\sum(y_i-\bar{y})^2}}=0.9993\)
Following the steps for finding correlation with Minitab you should get the following output:
| Pearson correlation | 0.999 |
| p-value | 0.000 |
9.2 - Simple Linear Regression
9.2 - Simple Linear RegressionStatisticians use models as a mathematical formula to describe the relationship between variables. Even with models, we never know the true relationship in practice. In this section, we will introduce the Simple Linear Regression (SLR) Model.
In simple linear regression, there is one quantitative response and one quantitative predictor variable, and we describe the relationship using a linear model. In the linear regression model view, we want to see what happens to the response variable when we change the predictor variable. If the value of the predictor variable increases, does the response tend to increase, decrease, or stay constant?
We use the slope to address whether or not there is a linear relationship between the two variables. If the average response variable does not change when we change the predictor variable, then the relationship is not a predictive one using a linear model. In other words, if the population slope is 0, then there is no linear relationship.
In this section, we present the model, hypotheses, and the assumptions for this test.
9.2.1 - The SLR Model
9.2.1 - The SLR ModelBefore we set up the model, we should clearly define our notation.
The variable \(X\) is the predictor variable and \(x_1, x_2, ...x_n\) are observed values of the predictor, \(X\).
The observations are considered as coordinates, \((x_i, y_i)\), for \(i=1, …, n\). As we saw before, the points, \((x_1,y_1), …,(x_n,y_n)\), may not fall exactly on a line, (like the weight and height example). There is some error we must consider.
We combine the linear relationship along with the error in the simple linear regression model.
- Simple Linear Regression Model
-
The general form of the simple linear regression model is...
\(Y=\beta_0+\beta_1X+\epsilon\)
For an individual observation,
\(y_i=\beta_0+\beta_1x_i+\epsilon_i\)
where,
\(\beta_0\) is the population y-intercept,
\(\beta_1\) is the population slope, and
\(\epsilon_i\) is the error or deviation of \(y_i\) from the line, \(\beta_0+\beta_1x_i\).
To make inferences about these unknown population parameters, we must find an estimate for them. There are different ways to estimate the parameters from the sample. In this class, we will present the least squares method.
- Least Squares Line
- The least squares line is the line for which the sum of squared errors of predictions for all sample points is the least.
Using the least squares method, we can find estimates for the two parameters.
The formulas to calculate least squares estimates are:
Sample Slope
\(\hat{\beta}_1=\dfrac{\sum (x_i-\bar{x})(y_i-\bar{y})}{\sum (x_i-\bar{x})^2}\)
Sample Intercept
\(\hat{\beta}_0=\bar{y}-\hat{\beta}_1\bar{x}\)
Note! You will not be expected to memorize these formulas or to find the estimates by hand. We will use Minitab to find these estimates for you.
We estimate the population slope, \(\beta_1\), with the sample slope denoted \(\hat{\beta_1}\). The population intercept, \(\beta_0\), is estimated with the sample intercept denoted \(\hat{\beta_0}\). The intercept is often referred to as the constant or the constant term.
Once the parameters are estimated, we have the least square regression equation line (or the estimated regression line).
- Least Squares Regression Equation
- \(\hat{y}=\hat{\beta}_0+\hat{\beta}_1x\)
We can also use the least squares regression line to estimate the errors, called residuals.
- Residual
- \(\hat{\epsilon}_i=y_i-\hat{y}_i\) is the observed error, typically called the residual.
The graph below summarizes the least squares regression for the height and weight data. Select the icons to view the explanations of the different parts of the scatterplot and the least squares regression line. We will go through this example in more detail later in the Lesson.
9.2.2 - Interpreting the Coefficients
9.2.2 - Interpreting the CoefficientsOnce we have the estimates for the slope and intercept, we need to interpret them. Recall from the beginning of the Lesson what the slope of a line means algebraically. If the slope is denoted as \(m\), then
\(m=\dfrac{\text{change in y}}{\text{change in x}}\)
In other words, the slope of a line is the change in the y variable over the change in the x variable. If the change in the x variable is one, then the slope is:
\(m=\dfrac{\text{change in y}}{1}\)
The slope is interpreted as the change of y for a one unit increase in x. This is the same idea for the interpretation of the slope of the regression line.
Interpreting the slope of the regression equation, \(\hat{\beta}_1\)
\(\hat{\beta}_1\) represents the estimated increase in Y per unit increase in X. Note that the increase may be negative which is reflected when \(\hat{\beta}_1\) is negative.
Again going back to algebra, the intercept is the value of y when \(x = 0\). It has the same interpretation in statistics.
Interpreting the intercept of the regression equation, \(\hat{\beta}_0\)
\(\hat{\beta}_0\) is the \(Y\)-intercept of the regression line. When \(X = 0\) is within the scope of observation, \(\hat{\beta}_0\) is the estimated value of Y when \(X = 0\).
Note, however, when \(X = 0\) is not within the scope of the observation, the Y-intercept is usually not of interest.
Example 9-3: Student height and weight (Interpreting the coefficients)
Suppose we found the following regression equation for weight vs. height.
\(\hat{\text{weight }}=-222.5 +5.49\text{ height }\)
- Interpret the slope of the regression equation.
- Does the intercept have a meaningful interpretation? If so, interpret the value.
- A slope of 5.49 represents the estimated change in weight (in pounds) for every increase of one inch of height.
- A height of zero, or \(X = 0\) is not within the scope of the observation since no one has a height of 0. The value \(\hat{\beta}_0\) by itself is not of much interest other than being the constant term for the regression line.
If the slope of the line is positive, then there is a positive linear relationship, i.e., as one increases, the other increases. If the slope is negative, then there is a negative linear relationship, i.e., as one increases the other variable decreases. If the slope is 0, then as one increases, the other remains constant, i.e., no predictive relationship.
Therefore, we are interested in testing the following hypotheses:
\(H_0\colon \beta_1=0\)
\(H_a\colon \beta_1\ne0\)
There are some assumptions we need to check (other than the general form) to make inferences for the population parameters based on the sample values. We will discuss these topics in the next section.
9.2.3 - Assumptions for the SLR Model
9.2.3 - Assumptions for the SLR ModelIn this section, we will present the assumptions needed to perform the hypothesis test for the population slope:
\(H_0\colon \ \beta_1=0\)
\(H_a\colon \ \beta_1\ne0\)
We will also demonstrate how to verify if they are satisfied. To verify the assumptions, you must run the analysis in Minitab first.
Assumptions for Simple Linear Regression
- Linearity: The relationship between \(X\) and \(Y\) must be linear.
Check this assumption by examining a scatterplot of x and y.
- Independence of errors: There is not a relationship between the residuals and the \(Y\) variable; in other words, \(Y\) is independent of errors.
Check this assumption by examining a scatterplot of “residuals versus fits”; the correlation should be approximately 0. In other words, there should not look like there is a relationship.
- Normality of errors: The residuals must be approximately normally distributed.
Check this assumption by examining a normal probability plot; the observations should be near the line. You can also examine a histogram of the residuals; it should be approximately normally distributed.
- Equal variances: The variance of the residuals is the same for all values of \(X\).
Check this assumption by examining the scatterplot of “residuals versus fits”; the variance of the residuals should be the same across all values of the x-axis. If the plot shows a pattern (e.g., bowtie or megaphone shape), then variances are not consistent, and this assumption has not been met.
Example 9-4: Student height and weight (SLR Assumptions)
Recall that we would like to see if height is a significant linear predictor of weight. Check the assumptions required for simple linear regression.
The data can be found here university_ht_wt.txt.
The first three observations are:
| Height (inches) | Weight (pounds) |
|---|---|
| 72 | 200 |
| 68 | 165 |
| 69 | 160 |
To check the assumptions, we need to run the model in Minitab.
Using Minitab to Fit a Regression Model
To find the regression model using Minitab...
- To check linearity create the fitted line plot by choosing STAT> Regression> Fitted Line Plot.
- For the other assumptions run the regression model. Select Stat> Regression> Regression> Fit Regression Model
- In the 'Response' box, specify the desired response variable.
- In the 'Continuous Predictors' box, specify the desired predictor variable.
- Click Graphs.
- In 'Residuals plots', choose 'Four in one.'
- Select OK.
Note! Of the 'four in one' graphs, you will only need the Normal Probability Plot, and the Versus Fits graphs to check the assumptions 2-4.
The basic regression analysis output is displayed in the session window. But we will only focus on the graphs at this point.
The graphs produced allow us to check our assumptions.Assumption 1: Linearity - The relationship between height and weight must be linear.
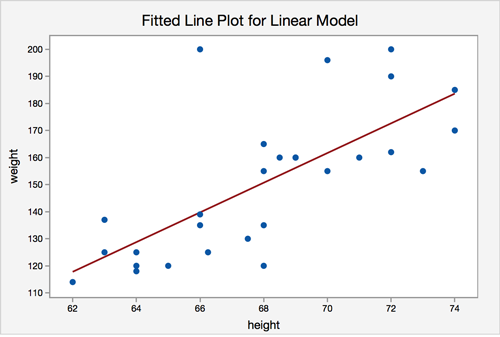
The scatterplot shows that, in general, as height increases, weight increases. There does not appear to be any clear violation that the relationship is not linear.
Assumption 2: Independence of errors - There is not a relationship between the residuals and weight.
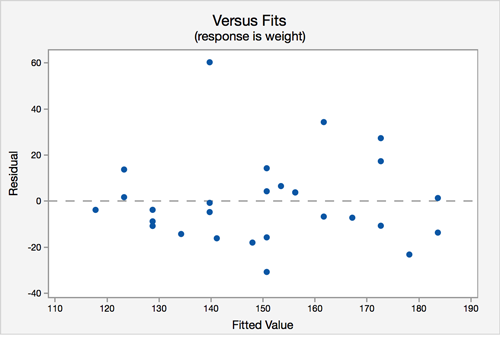
In the residuals versus fits plot, the points seem randomly scattered, and it does not appear that there is a relationship.
Assumption 3: Normality of errors - The residuals must be approximately normally distributed.
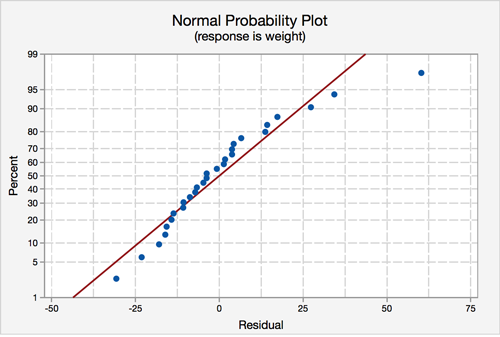
Most of the data points fall close to the line, but there does appear to be a slight curving. There is one data point that stands out.
Assumption 4: Equal Variances - The variance of the residuals is the same for all values of \(X\).
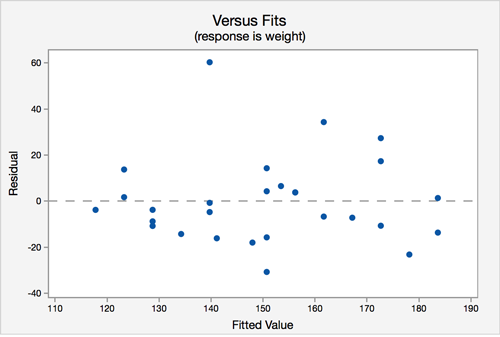
In this plot, there does not seem to be a pattern.
All of the assumption except for the normal assumption seem valid.
9.2.4 - Inferences about the Population Slope
9.2.4 - Inferences about the Population SlopeIn this section, we will present the hypothesis test and the confidence interval for the population slope. A similar test for the population intercept, \(\beta_0\), is not discussed in this class because it is not typically of interest.
|
Research Question |
Is there a linear relationship? |
Is there a positive linear relationship? |
Is there a negative linear relationship? |
|---|---|---|---|
|
Null Hypothesis |
\(\beta_1=0\) |
\(\beta_1=0\) |
\(\beta_1=0\) |
|
Alternative Hypothesis |
\(\beta_1\ne0\) |
\(\beta_1>0\) |
\(\beta_1<0\) |
|
Type of Test |
Two-tailed, non-directional |
Right-tailed, directional |
Left-tailed, directional |
The test statistic for the test of population slope is:
\(t^*=\dfrac{\hat{\beta}_1}{\hat{SE}(\hat{\beta}_1)}\)
where \(\hat{SE}(\hat{\beta}_1)\) is the estimated standard error of the sample slope (found in Minitab output). Under the null hypothesis and with the assumptions shown in the previous section, \(t^*\) follows a \(t\)-distribution with \(n-2\) degrees of freedom.
Note! In this class, we will have Minitab perform the calculations for this test. Minitab's output gives the result for two-tailed tests for \(\beta_1\) and \(\beta_0\). If you wish to perform a one-sided test, you would have to adjust the p-value Minitab provides.
- \( (1-\alpha)100\)% Confidence Interval for the Population Slope
-
The \( (1-\alpha)100\)% confidence interval for \(\beta_1\) is:
\(\hat{\beta}_1\pm t_{\alpha/2}\left(\hat{SE}(\hat{\beta}_1)\right)\)
where \(t\) has \(n-2\) degrees of freedom.
9.2.5 - Other Inferences and Considerations
9.2.5 - Other Inferences and ConsiderationsInferences about Mean Response for New Observation
Let’s go back to the height and weight example:
Example
If you are asked to estimate the weight of a STAT 500 student, what will you use as a point estimate? If I tell you that the height of the student is 70 inches, can you give a better estimate of the person's weight?
Now that we have our regression equation, we can use height to provide a better estimate of weight. We would want to report a mean response value for the provided height, i.e 70 inches.
The mean response at a given X value is given by:
\(E(Y)=\beta_0+\beta_1X\)
This is an unknown but fixed value. The point estimate for mean response at \(X=x\) is given by \(\hat{\beta}_0+\hat{\beta}_1x\).
The example for finding this mean response for height and weight is shown later in the lesson.
Inferences about Outcome for New Observation
The point estimate for the outcome at \(X = x\) is provided above. The interval to estimate the mean response is called the confidence interval. Minitab calculates this for us.
The interval used to estimate (or predict) an outcome is called prediction interval. For a given x value, the prediction interval and confidence interval have the same center, but the width of the prediction interval is wider than the width of the confidence interval. That makes good sense since it is harder to estimate a value for a single subject (say predict your weight based on your height) than it would be to estimate the average for subjects (say predict the mean weight of people who are your height). Again, Minitab will calculate this interval as well.
Cautions with Linear Regression
First, use extrapolation with caution. Extrapolation is applying a regression model to X-values outside the range of sample X-values to predict values of the response variable \(Y\). For example, you would not want to use your age (in months) to predict your weight using a regression model that used the age of infants (in months) to predict their weight.
Second, the fact that there is no linear relationship (i.e. correlation is zero) does not imply there is no relationship altogether. The scatter plot will reveal whether other possible relationships may exist. The figure below gives an example where X, Y are related, but not linearly related i.e. the correlation is zero.
Outliers and Influential Observations
Influential observations are points whose removal causes the regression equation to change considerably. It is flagged by Minitab in the unusual observation list and denoted as X. Outliers are points that lie outside the overall pattern of the data. Potential outliers are flagged by Minitab in the unusual observation list and denoted as R.
The following is the Minitab output for the unusual observations within the height and weight example:
Fits and Diagnostics for Unusual Observations
Obs | weight | Fit | Residual | St Resid |
24 | 200.00 | 139.74 | 60.26 | 3.23R |
R Large Residual
Some observations may be both outliers and influential, and these are flagged by R and X (R X). Those observational points will merit particular attention. In our height and weight example, we have an R (potential outlier) observation, but it is not an influential point (RX observation).
Estimating the standard deviation of the error term
Our simple linear regression model is:
\(Y=\beta_0+\beta_1X+\epsilon\)
The errors for the \(n\) observations are denoted as \(\epsilon_i\), for \(i=1, …, n\). One of our assumptions is that the errors have equal variance (or equal standard deviation). We can estimate the standard deviation of the error by finding the standard deviation of the residuals, \(\epsilon_i=y_i-\hat{y}_i\). Minitab also provides the estimate for us, denoted as \(S\), under the Model Summary. We can also calculate it by:
\(s=\sqrt{\text{MSE}}\)
Find the MSE in the ANOVA table, under the MS column and the Error row.
9.2.6 - Examples
9.2.6 - ExamplesIn this section, we present an example and review what we have covered so far in the context of the example.
Example 9-5: Student height and weight (SLR)
We will continue with our height and weight example. Answer the following questions.
- Is height a significant linear predictor of weight? Conduct the test at a significance level of 5%. State the regression equation.
- Does \(\beta_0\) have a meaningful interpretation?
- Find the confidence interval for the population slope and interpret it in the context of the problem.
- If a student is 70 inches, what weight could we expect?
- What is the estimated standard deviation of the error?
The model for this problem is:
\(\text{weight}=\beta_0+\beta_1\text{height}+\epsilon\)
The hypotheses we are testing are:
\(H_0\colon \beta_1=0\)
\(H_a\colon \beta_1\ne 0\)
Recall that we previously examined the assumptions. Here is a summary of what we presented before:
Assumptions
Linearity: The relationship between height and weight must be linear.
The scatterplot shows that, in general, as height increases, weight increases. There does not appear to be any clear violation that the relationship is not linear.
Independence of errors: There is not a relationship between the residuals and weight.
In the residuals versus fits plot, the points seem randomly scattered, and it does not appear that there is a relationship.
Normality of errors: The residuals must be approximately normally distributed.
Most of the data points fall close to the line, but there does appear to be a slight curving. There is one data point that clearly stands out. In the histogram, we can see that, with that one observation, the shape seems slightly right-skewed.
- Equal variances: The variance of the residuals is the same for all values of \(X\).
In this plot, there does not seem to be a pattern.
All of the assumption except for the normal assumption seem valid.
Minitab output for the height and weight data:
Model Summary
S
R-sq
R-sq(adj)
R-sq(pred)
19.1108
50.57%
48.67%
44.09%
Coefficients
Team
Coef
SE Coef
T-Value
P-Value
VIF
Constant
-222.5
72.4
-3.07
0.005
height
5.49
1.06
5.16
0.000
1.00
Regression Equation
\(\hat{\text{weight}} = -222.5+5.49\text{height}\)
The regression equation is:
\(\hat{\text{weight}}=-222.5+5.49\text{height}\)
The slope is 5.49, and the intercept is -222.5. The test for the slope has a p-value of less than 0.001. Therefore, with a significance level of 5%, we can conclude that there is enough evidence to suggest that height is a significant linear predictor of weight. We should make this conclusion with caution, however, since one of our assumptions might not be valid.
- The intercept is -222.5. Therefore, when height is equal to 0, then a person’s weight is predicted to be -222.5 pounds. It is also not possible for someone to have a height of 0 inches. Therefore, the intercept does not have a valid meaning.
The confidence interval for the population slope is:
\(\hat{\beta}_1\pm t_{\alpha/2}\hat{SE}(\hat{\beta}_1)\)
The estimate for the slope is 5.49 and the standard error for the estimate (SE Coef in the output) is 1.06. There are \(n=28\) observations so the degrees of freedom are \(28-2=26\). Using Minitab, we find the t-value to be 2.056. Putting the pieces together, the interval is:
\(5.49\pm 2.056(1.06)\)
\((3.31, 7.67)\)
We are 95% confident that the population slope is between 3.31 and 7.67. In other words, we are 95% confident that, as height increases by one inch, that weight increases by between 3.31 and 7.67 pounds, on average.
Using the regression formula with a height equal to 70 inches, we get:
\(\hat{\text{weight}}=-222.5+5.49(70)=161.8\)
A student with a height of 70 inches, we would expect a weight of 162.3 pounds. If we wanted, we could have Minitab produce a confidence interval for this estimate. We will leave this out for this example.
Using the output, under the model summary:
\(s=19.1108\)
Try it!
The No-Lemon used car dealership in a college town records the age (in years) and price for cars it sold in the last year (cars_sold.txt). Here is a table of this data.
age | 4 | 4 | 4 | 5 | 5 | 6 | 7 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
price | 6200 | 5700 | 6800 | 5600 | 4500 | 4900 | 4600 | 4300 | 4200 |
age | 8 | 8 | 9 | 9 | 10 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|
price | 4500 | 4000 | 3200 | 3100 | 2500 | 2100 | 2600 | 2400 | 2200 |
Using the data above, answer the following questions.
- Is age a significant negative linear predictor of price? Conduct the test at a significance level of 5%.
- Does \(\beta_0\) have a meaningful interpretation?
- Find the confidence interval for the population slope and interpret it in context of the problem.
- If a car is seven years old, what price could we expect?
- What is the estimate of the standard deviation of the errors?
The linear regression model is:
\(\text{price}=\beta_0+\beta_1\text{age}+\epsilon\)
To test whether age is a statistically significant negative linear predictor of price, we can set up the following hypotheses:.
\(H_0\colon \beta_1=0\)
\(H_a\colon \beta_1< 0\)
We need to verify that our assumptions are satisfied. Let's do this in Minitab. Remember, we have to run the linear regression analysis to check the assumptions.
Assumption 1: Linearity
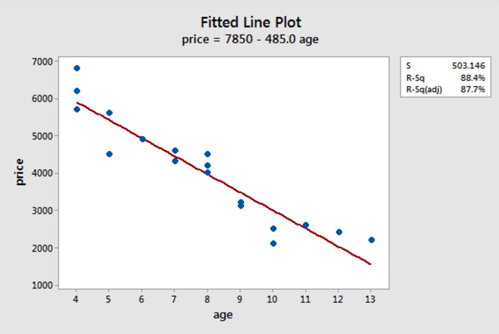
The scatterplot below shows that the relationship between age and price scores is linear. There appears to be a strong negative linear relationship and no obvious outliers.
Assumption 2: Independence of errors
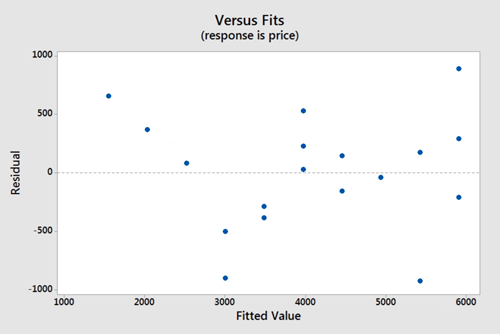
There does not appear to be a relationship between the residuals and the fitted values. Thus, this assumption seems valid.
Assumption 3: Normality of errors
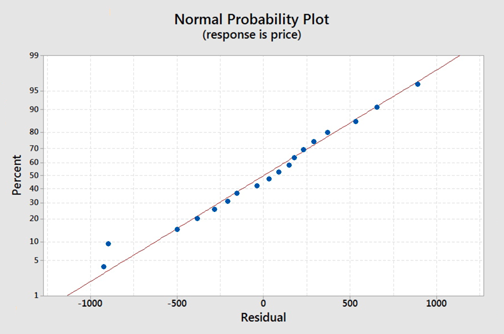
On the normal probability plot we are looking to see if our observations follow the given line. This graph does not indicate that there is a violation of the assumption that the errors are normal. If a probability plot is not an option we can refer back to one of our first lessons on graphing quantitative data and use a histogram or boxplot to examine if the residuals appear to follow a bell shape.
Assumption 4: Equal Variances
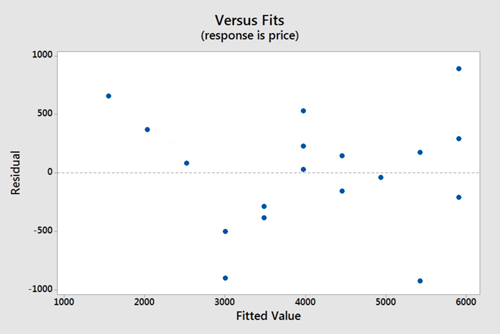
Again we will use the plot of residuals versus fits. Now we are checking that the variance of the residuals is consistent across all fitted values. This assumption seems valid.
Model Summary
S | R-sq | R-sq(adj) | R-sq(pred) |
|---|---|---|---|
503.146 | 88.39% | 87.67% | 84.41% |
Coefficients
Team | Coef | SE Coef | T-Value | P-Value | VIF |
|---|---|---|---|---|---|
Constant | 7850 | 362 | 21.70 | 0.000 | |
age | -485.0 | 43.9 | -11.04 | 0.000 | 1.00 |
Regression Equation
\(\hat{\text{price}} = 7850 - 485.0 \text{age}\)
From the output above we can see that the p-value of the coefficient of age is 0.000 which is less than 0.001. The Minitab output is for a two-tailed test and we are dealing with a left-tailed test. Therefore, the p-value for the left-tailed test is less than \(\frac{0.001}{2}\) or less than 0.0005.
We can thus conclude that age (in years) is a statistically significant negative linear predictor of price for any reasonable \(\alpha\) value.
The 95% confidence interval for the population slope is:
\(\hat{\beta}_1\pm t_{\alpha/2}\text{SE}(\hat{\beta}_1)\)
Using the output, \(\hat{\beta}_1=-485\) and the \(\text{SE}(\hat{\beta}_1)=43.9\). We need to have \(t_{\alpha/2}\) with \(n-2\) degrees of freedom. In this case, there are 18 observations so the degrees of freedom are \(18-2=16\). Using software, we find \(t_{\alpha/2}=2.12\).
The 95% confidence interval is:
\(-485\pm 2.12(43.9)\)
\((-578.068, -391.932)\)
We are 95% confident that the population slope for the regression model is between -578.068 and -391.932. In other words, we are 95% confident that, for every one year increase in age, the price of a vehicle will decrease between 391.932 and 578.068 dollars.
We can use the regression equation with \(\text{age}=7\):
\(\hat{\text{price}}=7850-485(7)=4455\)
We can expect the price to be $4455.
The residual standard error is estimated by s, which is calculated as:
\(s=\sqrt{\text{MSE}}=\sqrt{253156}=503.146\)
It is also shown as \(s\) under the model summary in the output.
9.3 - Coefficient of Determination
9.3 - Coefficient of DeterminationNow that we know how to estimate the coefficients and perform the hypothesis test, is there any way to tell how useful the model is?
One measure is the coefficient of determination, denoted \(R^2\).
Coefficient of Determination \(R^2\)
The coefficient of determination measures the percentage of variability within the \(y\)-values that can be explained by the regression model.
Therefore, a value close to 100% means that the model is useful and a value close to zero indicates that the model is not useful.
It can be shown by mathematical manipulation that:
\(\text{SST }=\text{ SSR }+\text{ SSE}\)
\(\sum (y_i-\bar{y})^2=\sum (\hat{y}_i-\bar{y})^2+\sum (y_i-\hat{y}_i)^2\)
Total variability in the y value = Variability explained by the model + Unexplained variability
To get the total, explained and unexplained variability, first we need to calculate corresponding deviances. Drag the slider on the image below to see how the total deviance \((y_i-\bar{y})\) is split into explained \((\hat{y}_i-\bar{y})\) and unexplained deviances \((y_i-\hat{y}_i)\).
The breakdown of variability in the above equation holds for the multiple regression model also.
Coefficient of Determination \(R^2\) Formula
\(R^2=\dfrac{\text{variability explained by the model}}{\text{total variability in the y values}}\)
\(R^2\) represents the proportion of total variability of the \(y\)-value that is accounted for by the independent variable \(x\).
For the specific case when there is only one independent variable \(X\) (i.e., simple linear regression), one can show that \(R^2 =r^2\), where \(r\) is correlation coefficient between \(X\) and \(Y\).
Example 9-6: Student height and weight (\(R^2\))
Let's take a look at Minitab's output from the height and weight example (university_ht_wt.TXT) that we have been working with in this lesson.
Model Summary
S | R-sq | R-sq(adj) | R-sq(pred) |
|---|---|---|---|
19.1108 | 50.57% | 48.67% | 44.09% |
Coefficients
Team | Coef | SE Coef | T-Value | P-Value | VIF |
|---|---|---|---|---|---|
Constant | -222.5 | 72.4 | -3.07 | 0.005 | |
height | 5.49 | 1.06 | 5.16 | 0.000 | 1.00 |
Regression Equation
weight = -222.5 + 5.49 height
Find the coefficient of determination and interpret the value.
The coefficient of determination, \(R^2\) is 0.5057 or 50.57%. This value means that 50.57% of the variation in weight can be explained by height.
Remember, for this example we found the correlation value, \(r\), to be 0.711.
So, we can now see that \(r^2 = (0.711)^2 = .506\) which is the same reported for R-sq in the Minitab output.
Try it!
Used car sales continued...
For the age and price of the car example (cars_sold.txt), what is the value of the coefficient of determination and interpret the value in the context of the problem?
Model Summary
S | R-sq | R-sq(adj) | R-sq(pred) |
|---|---|---|---|
503.146 | 88.39% | 87.67% | 84.41% |
Coefficients
Team | Coef | SE Coef | T-Value | P-Value | VIF |
|---|---|---|---|---|---|
Constant | 7850 | 362 | 21.70 | 0.000 | |
age | -485.0 | 43.9 | -11.04 | 0.000 | 1.00 |
Regression Equation
price = 7850 - 485.0 age
From the Minitab output, we see an R-sq value of 88.39%. We want to report this in terms of the study, so here we would say that 88.39% of the variation in vehicle price is explained by the age of the vehicle.
9.4 - Inference for Correlation
9.4 - Inference for CorrelationLet’s review the notation for correlation.
\(r\): The sample correlation (Pearson’s correlation)
\(\rho\): “rho” is the population correlation
The sample correlation is found by:
\( r=\dfrac{\sum (x_i-\bar{x})(y_i-\bar{y}) }{\sqrt{\sum (x_i-\bar{x})^2}\sqrt{\sum (y_i-\bar{y})^2}} \)
In this section, we will present a hypothesis test for the population correlation. Then, we will compare the tests and interpretations for the slope and correlation.
9.4.1 - Hypothesis Testing for the Population Correlation
9.4.1 - Hypothesis Testing for the Population CorrelationIn this section, we present the test for the population correlation using a test statistic based on the sample correlation.
As with all hypothesis test, there are underlying assumptions. The assumptions for the test for correlation are:
- The are no outliers in either of the two quantitative variables.
- The two variables should follow a normal distribution
If there is no linear relationship in the population, then the population correlation would be equal to zero.
\(H_0\colon \rho=0\) (\(X\) and \(Y\) are linearly independent, or X and Y have no linear relationship)
\(H_a\colon \rho\ne0\) (\(X\) and \(Y\) are linearly dependent)
|
Research Question |
Is there a linear relationship? |
Is there a positive linear relationship? |
Is there a negative linear relationship? |
|---|---|---|---|
|
Null Hypothesis |
\(\rho=0\) |
\(\rho=0\) |
\(\rho=0\) |
|
Alternative Hypothesis |
\(\rho\ne0\) |
\(\rho>0\) |
\(\rho<0\) |
|
Type of Test |
Two-tailed, non-directional |
Right-tailed, directional |
Left-tailed, directional |
Under the null hypothesis and with above assumptions, the test statistic, \(t^*\), found by:
\(t^*=\dfrac{r\sqrt{n-2}}{\sqrt{1-r^2}}\)
which follows a \(t\)-distribution with \(n-2\) degrees of freedom.
As mentioned before, we will use Minitab for the calculations. The output from Minitab previously used to find the sample correlation also provides a p-value. This p-value is for the two-sided test. If the alternative is one-sided, the p-value from the output needs to be adjusted.
Example 9-7: Student height and weight (Tests for \(\rho\))
For the height and weight example (university_ht_wt.TXT), conduct a test for correlation with a significance level of 5%.
The output from Minitab is:
Correlation: height, weight
Correlations
P-value
0.000
For the sake of this example, we will find the test statistic and the p-value rather than just using the Minitab output. There are 28 observations.
The test statistic is:
\begin{align} t^*&=\dfrac{r\sqrt{n-2}}{\sqrt{1-r^2}}\\&=\dfrac{(0.711)\sqrt{28-2}}{\sqrt{1-0.711^2}}\\&=5.1556 \end{align}
Next, we need to find the p-value. The p-value for the two-sided test is:
\(\text{p-value}=2P(T>5.1556)<0.0001\)
Therefore, for any reasonable \(\alpha\) level, we can reject the hypothesis that the population correlation coefficient is 0 and conclude that it is nonzero. There is evidence at the 5% level that Height and Weight are linearly dependent.
Try it!
For the sales and advertising example, conduct a test for correlation with a significance level of 5% with Minitab.
Sales units are in thousands of dollars, and advertising units are in hundreds of dollars.
| Sales (Y) | Advertising (X) |
|---|---|
| 1 | 1 |
| 1 | 2 |
| 2 | 3 |
| 2 | 4 |
| 4 | 5 |
Correlation: Y,X
Correlations
P-value
0.035
The sample correlation is 0.904. This value indicates a strong positive linear relationship between sales and advertising.
For the Sales (Y) and Advertising (X) data, the test statistic is...
\(t^*=\dfrac{(0.904)\sqrt{5-2}}{\sqrt{1-(0.904)^2}}=3.66\)
...with df of 3, we arrive at a p-value = 0.035. For \(\alpha=0.05\), we can reject the hypothesis that the population correlation coefficient is 0 and conclude that it is nonzero, i.e., conclude that sales and advertising are linearly dependent.
9.4.2 - Comparing Correlation and Slope
9.4.2 - Comparing Correlation and SlopeSome of you may have noticed that the hypothesis test for correlation and slope are very similar. Also, the test statistic for both tests follows the same distribution with the same degrees of freedom, \(n-2\).
This similarity is because the two values are mathematically related. In fact,
\(\hat{\beta}_1=r\dfrac{\sqrt{\sum (y_i-\bar{y})^2}}{\sqrt{\sum(x_i-\bar{x})^2}}\)
Here is a summary of some of the similarities and differences between the sample correlation and the sample slope.
Similarities
- The test for correlation will lead to the same conclusion as the test for slope.
- The sign of the slope (i.e. negative or positive) will be the same for the correlation. In other words, both values indicate the direction of the relationship
Differences
- The value of the correlation indicates the strength of the linear relationship. The value of the slope does not.
- The slope interpretation tells you the change in the response for a one-unit increase in the predictor. Correlation does not have this kind of interpretation.
9.5 - Multiple Regression Model
9.5 - Multiple Regression ModelMultiple Linear Regression Model
In this section, we (very) briefly discuss Multiple Linear Regression. In practice, it is not usual that there is only one predictor variable. In Multiple Linear Regression, there is one quantitative response and more than one predictor or independent variable. The model will contain the constant or intercept term, \(\beta_0\), and more than one coefficient, denoted \(\beta_1, …, \beta_k\), where \(k\) is the number of predictors.
- Multiple Linear Regression Model
- \(Y=\beta_0+\beta_1X_1+...+\beta_kX_k+\epsilon\)
Where \(Y\) is the response variable and \(X_1, …, X_k\) are independent variables. \(\beta_0, \beta_1, …, \beta_k\) are fixed (but unknown) parameters, and \(\epsilon\) is a random variable that is normally distributed with mean 0 and having a variance \(\sigma^2_\epsilon\).
F-Test for Overall Significance
There is a statistical test we can use to determine the overall significance of the regression model.
The F-test in Multiple Linear Regression test the following hypotheses:
\(H_0\colon \beta_1=...=\beta_k=0\)
\(H_a\colon \text{ At least one }\beta_i\text{ is not equal to zero}\)
The test statistic for this test, denoted \(F^*\), follows an \(F\) distribution.
We will not expect you to understand Multiple Linear Regression. We included it here to show you what you may see in practice. If you are interested in learning more, you can take STAT 501: Regression Methods.
9.6 - Lesson 9 Summary
9.6 - Lesson 9 SummaryIn this Lesson, we examined the relationship between a quantitative response (or dependent variable) and a quantitative explanatory variable (or independent variable). We are interested in whether or not the independent variable is a significant linear predictor of the response.
In the next Lesson, we consider a different situation. We look back on the example where we have a quantitative response and an explanatory variable with more than two levels. In other words, we look at the situation where we are comparing means from more than two groups.