3.2 - Discrete Probability Distributions
3.2 - Discrete Probability DistributionsThis section takes a look at some of the characteristics of discrete random variables.
Consider the data set with the values: \(0, 1, 2, 3, 4\). If \(X\) is a random variable of a random draw from these values, what is the probability you select 2? If we assume the probabilities of each of the values is equal, then the probability would be \(P(X=2)=\frac{1}{5}\). We can define the probabilities of each of the outcomes using the probability mass function (PMF) described in the last section. If we assume the probabilities of all the outcomes were the same, the PMF could be displayed in function form or a table. As a function, it would look like: \(f(x)=\begin{cases} \frac{1}{5} & x=0, 1, 2, 3, 4\\ 0 & \text{otherwise} \end{cases}\)
As a table, it would look like:
| \(x\) | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| \(f(x)\) | 1/5 | 1/5 | 1/5 | 1/5 | 1/5 |
Recall that for a PMF, \(f(x)=P(X=x)\). In other words, the PMF gives the probability our random variable is equal to a value, x. We can also find the CDF using the PMF.
Example 3-1: CDF
Find the CDF, in tabular form of the random variable, X, as defined above.
| \(x\) | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| \(f(x) = P(X=x)\) | 1/5 | 1/5 | 1/5 | 1/5 | 1/5 |
Answer
Recall that \(F(X)=P(X\le x)\). Start by finding the CDF at \(x=0\).
\(F(0)=P(X\le 0)\)
Since 0 is the smallest value of \(X\), then \(F(0)=P(X\le 0)=P(X=0)=\frac{1}{5}\)
Now, find \(F(1)\).
\begin{align} F(1)=P(X\le 1)&=P(X=1)+P(X=0)\\&=\frac{1}{5}+\frac{1}{5}\\&=\frac{2}{5}\end{align}
Next, \(F(2)\).
\begin{align} F(2)=P(X\le 2)&=P(X=2)+P(X=1)+P(X=0)\\&=\frac{1}{5}+\frac{1}{5}+\frac{1}{5}\\&=\frac{3}{5}\end{align}
Next, \(F(3)\).
\begin{align} F(3)=P(X\le 3)&=P(X=3)+P(X=2)+P(X=1)+P(X=0)\\&=\frac{1}{5}+\frac{1}{5}+\frac{1}{5}+\frac{1}{5}\\&=\frac{4}{5}\end{align}
Finally, \(F(4)\).
\begin{align} F(4)=P(X\le 4)&=P(X=4)+P(X=3)+P(X=2)+P(X=1)+P(X=0)\\&=\frac{1}{5}+\frac{1}{5}+\frac{1}{5}+\frac{1}{5}+\frac{1}{5}\\&=\frac{5}{5}=1\end{align}
In table form...
| \(x\) | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| \(F(x) = P(X\le x)\) | 1/5 | 2/5 | 3/5 | 4/5 | 5/5=1 |
This table provides the probability of each outcome and those prior to it. Thus, the probability for the last event in the cumulative table is 1 since that outcome or any previous outcomes must occur.
Try It!
Use the table from the example above to answer the following questions.
| \(x\) | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| \(f(x) = P(X=x)\) | 1/5 | 1/5 | 1/5 | 1/5 | 1/5 |
-
Find \(P(X=1)\)
\(P(X=1)=\dfrac{1}{5}\)
-
Find \(P(X\le 2)\)\begin{align} P(X\le 2)&=P(X=0)+P(X=1)+P(X=2)\\&=\dfrac{1}{5}+\dfrac{1}{5}+\dfrac{1}{5}\\&=\dfrac{3}{5}\end{align}
-
\(P(X<3)\)
\(P(X<3)=P(X\le 2)=\dfrac{3}{5}\). Note that \(P(X<3)\) does not equal \(P(X\le 3)\) as it does not include \(P(X=3)\).
-
\(P(1\le X\le 3)\)\(P(1\le X\le 3)=P(X=1)+P(X=2)+P(X=3)=\dfrac{3}{5}\)
3.2.1 - Expected Value and Variance of a Discrete Random Variable
3.2.1 - Expected Value and Variance of a Discrete Random VariableBy continuing with example 3-1, what value should we expect to get? What would be the average value?
We can answer this question by finding the expected value (or mean).
- Expected Value (or mean) of a Discrete Random Variable
-
For a discrete random variable, the expected value, usually denoted as \(\mu\) or \(E(X)\), is calculated using:
-
\(\mu=E(X)=\sum x_if(x_i)\)
- The formula means that we multiply each value, \(x\), in the support by its respective probability, \(f(x)\), and then add them all together. It can be seen as an average value but weighted by the likelihood of the value.
-
Example 3-2: Expected Value
In Example 3-1 we were given the following discrete probability distribution:
| \(x\) | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| \(f(x)\) | 1/5 | 1/5 | 1/5 | 1/5 | 1/5 |
What is the expected value?
Answer
\begin{align} \mu=E(X)=\sum xf(x)&=0\left(\frac{1}{5}\right)+1\left(\frac{1}{5}\right)+2\left(\frac{1}{5}\right)+3\left(\frac{1}{5}\right)+4\left(\frac{1}{5}\right)\\&=2\end{align}
For this example, the expected value was equal to a possible value of X. This may not always be the case. For example, if we flip a fair coin 9 times, how many heads should we expect? We will explain how to find this later but we should expect 4.5 heads. The expected value in this case is not a valid number of heads.
Now that we can find what value we should expect, (i.e. the expected value), it is also of interest to give a measure of the variability.
- Variance of a Discrete Random Variable
-
The variance of a discrete random variable is given by:
-
\(\sigma^2=\text{Var}(X)=\sum (x_i-\mu)^2f(x_i)\)
-
The formula means that we take each value of x, subtract the expected value, square that value and multiply that value by its probability. Then sum all of those values.
There is an easier form of this formula we can use.
\(\sigma^2=\text{Var}(X)=\sum x_i^2f(x_i)-E(X)^2=\sum x_i^2f(x_i)-\mu^2\)
The formula means that first, we sum the square of each value times its probability then subtract the square of the mean. We will use this form of the formula in all of our examples.
-
- Standard Deviation of a Discrete Random Variable
-
The standard deviation of a random variable, $X$, is the square root of the variance.
- \(\sigma=\text{SD}(X)=\sqrt{\text{Var}}(X)=\sqrt{\sigma^2}\)
Example 3-3: Standard Deviation
Consider the first example where we had the values 0, 1, 2, 3, 4. The PMF in tabular form was:
| \(x\) | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| \(f(x)\) | 1/5 | 1/5 | 1/5 | 1/5 | 1/5 |
Find the variance and the standard deviation of X.
Answer
\(\text{Var}(X)=\left[0^2\left(\dfrac{1}{5}\right)+1^2\left(\dfrac{1}{5}\right)+2^2\left(\dfrac{1}{5}\right)+3^2\left(\dfrac{1}{5}\right)+4^2\left(\dfrac{1}{5}\right)\right]-2^2=6-4=2\)
\(\text{SD}(X)=\sqrt{2}\approx 1.4142\)
Example 3-4: Prior Convictions
Click on the tab headings to see how to find the expected value, standard deviation, and variance. The last tab is a chance for you to try it.

Let X = number of prior convictions for prisoners at a state prison at which there are 500 prisoners. (\(x = 0,1,2,3,4\))
| \(X=x\) | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| \(Number\ of\ Prisoners\) | 80 | 265 | 100 | 40 | 15 |
| \(f(x) = P(X=x)\) | 80/500 | 265/500 | 100/500 | 40/500 | 15/500 |
| \(f(x)=P(X=x)\) | 0.16 | 0.53 | 0.2 | 0.08 | 0.03 |
What is the expected value for number of prior convictions?
| \(X=x\) | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| \(Number\ of\ Prisoners\) | 80 | 265 | 100 | 40 | 15 |
| \(f(x) = P(X=x)\) | 80/500 | 265/500 | 100/500 | 40/500 | 15/500 |
| \(f(x)=P(X=x)\) | 0.16 | 0.53 | 0.2 | 0.08 | 0.03 |
Answer
For this we need a weighted average since not all the outcomes have equal chance of happening (i.e. they are not equally weighted). So, we need to find our expected value of \(X\), or mean of \(X\), or \(E(X) = \Sigma f(x_i)(x_i)\). When we write this out it follows:
\(=(0.16)(0)+(0.53)(1)+(0.2)(2)+(0.08)(3)+(0.03)(4)=1.29\)
Calculate the variance and the standard deviation for the Prior Convictions example:
| \(X=x\) | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| \(Number\ of\ Prisoners\) | 80 | 265 | 100 | 40 | 15 |
| \(f(x) = P(X=x)\) | 80/500 | 265/500 | 100/500 | 40/500 | 15/500 |
| \(f(x)=P(X=x)\) | 0.16 | 0.53 | 0.2 | 0.08 | 0.03 |
Answer
Using the data in our example we find that...
\begin{align} \text{Var}(X) &=[0^2(0.16)+1^2(0.53)+2^2(0.2)+3^2(0.08)+4^2(0.03)]–(1.29)^2\\ &=2.53–1.66\\ &=0.87\\ \text{SD}(X) &=\sqrt(0.87)\\ &=0.93 \end{align}
What is the expected number of prior convictions? Below is the probability distribution table for the prior conviction data. Use this table to answer the questions that follow.
| \(X=x\) | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| \(f(x)=P(X=x)\) | 0.16 | 0.53 | 0.2 | 0.08 | 0.03 |
3.2.2 - Binomial Random Variables
3.2.2 - Binomial Random VariablesA binary variable is a variable that has two possible outcomes. For example, sex (male/female) or having a tattoo (yes/no) are both examples of a binary categorical variable.
A random variable can be transformed into a binary variable by defining a “success” and a “failure”. For example, consider rolling a fair six-sided die and recording the value of the face. The random variable, value of the face, is not binary. If we are interested, however, in the event A={3 is rolled}, then the “success” is rolling a three. The failure would be any value not equal to three. Therefore, we can create a new variable with two outcomes, namely A = {3} and B = {not a three} or {1, 2, 4, 5, 6}. This new variable is now a binary variable.
Binary Categorical Variable
A binary categorical variable is a variable that has two possible outcomes.
The Binomial Distribution
The binomial distribution is a special discrete distribution where there are two distinct complementary outcomes, a “success” and a “failure”.
We have a binomial experiment if ALL of the following four conditions are satisfied:
- The experiment consists of n identical trials (n is fixed).
- Each trial results in one of the two outcomes, called success and failure.
- The probability of success, denoted p, remains the same from trial to trial.
- The n trials are independent. That is, the outcome of any trial does not affect the outcome of the others.
If the four conditions are satisfied, then the random variable \(X\)=number of successes in \(n\) trials, is a binomial random variable with
\begin{align}
&\mu=E(X)=np &&\text{(Mean)}\\
&\text{Var}(X)=np(1-p) &&\text{(Variance)}\\
&\text{SD}(X)=\sqrt{np(1-p)} \text{, where \(p\) is the probability of the “success."} &&\text{(Standard Deviation)}\\
\end{align}
A Note on Notation! Some common notation for “success” that you may see will be either \(p\) or \(\pi\) to represent the probability of “success” and usually \(q=1-p\) to represent the probability of “failure”. \(\pi\) is what is used in text. “Success” is defined as whatever the researcher decides…not just a positive outcome. The symbol \(\pi\) is this case does NOT refer the numerical value 3.14
\(p \;(or\ \pi)\) = probability of success
Example 3-5: Prior Convictions
Let's use the example from the previous page investigating the number of prior convictions for prisoners at a state prison at which there were 500 prisoners. Define the “success” to be the event that a prisoner has no prior convictions. Find \(p\) and \(1-p\).
Answer
Let Success = no priors (0)
Let Failure = priors (1, 2, 3, or 4)
Looking back on our example, we can find that:
\(p=0.16\)
\(1-p=1-0.16=0.84\)
Verify by \(p+(1-p)=1\)
Example 3-6: Crime Survey
An FBI survey shows that about 80% of all property crimes go unsolved. Suppose that in your town 3 such crimes are committed and they are each deemed independent of each other. What is the probability that 1 of 3 of these crimes will be solved?
First, we must determine if this situation satisfies ALL four conditions of a binomial experiment:
- Does it satisfy a fixed number of trials? YES the number of trials is fixed at 3 (n = 3.)
- Does it have only 2 outcomes? YES (Solved and unsolved)
- Do all the trials have the same probability of success? YES (p = 0.2)
- Are all crimes independent? YES (Stated in the description.)
To find the probability that only 1 of the 3 crimes will be solved we first find the probability that one of the crimes would be solved. With three such events (crimes) there are three sequences in which only one is solved:
- Solved First, Unsolved Second, Unsolved Third = (0.2)(0.8)( 0.8) = 0.128
- Unsolved First, Solved Second, Unsolved Third = (0.8)(0.2)(0.8) = 0.128
- Unsolved First, Unsolved Second, Solved Third = (0.8)(0.8)(0.2) = 0.128
We add these 3 probabilities up to get 0.384. Looking at this from a formula standpoint, we have three possible sequences, each involving one solved and two unsolved events. Putting this together gives us the following: \(3(0.2)(0.8)^2=0.384\)
The example above and its formula illustrates the motivation behind the binomial formula for finding exact probabilities.
The Binomial Formula
For a binomial random variable with probability of success, \(p\), and \(n\) trials...
\(f(x)=P(X = x)=\dfrac{n!}{x!(n−x)!}p^x(1–p)^{n-x}\) for \(x=0, 1, 2, …, n\)
Graphical Displays of Binomial Distributions
The formula defined above is the probability mass function, pmf, for the Binomial. We can graph the probabilities for any given \(n\) and \(p\). The following distributions show how the graphs change with a given n and varying probabilities.
Example 3-7: Crime Survey Continued...
For the FBI Crime Survey example, what is the probability that at least one of the crimes will be solved?
Answer
Here we are looking to solve \(P(X \ge 1)\).
There are two ways to solve this problem: the long way and the short way.
The long way to solve for \(P(X \ge 1)\). This would be to solve \(P(x=1)+P(x=2)+P(x=3)\) as follows:
\(P(x=1)=\dfrac{3!}{1!2!}0.2^1(0.8)^2=0.384\)
\(P(x=2)=\dfrac{3!}{2!1!}0.2^2(0.8)^1=0.096\)
\(P(x=3)=\dfrac{3!}{3!0!}0.2^3(0.8)^0=0.008\)
We add up all of the above probabilities and get 0.488...OR...we can do the short way by using the complement rule. Here the complement to \(P(X \ge 1)\) is equal to \(1 - P(X < 1)\) which is equal to \(1 - P(X = 0)\). We have carried out this solution below.
\begin{align} 1–P(x<1)&=1–P(x=0)\\&=1–\dfrac{3!}{0!(3−0)!}0.2^0(1–0.2)^3\\ &=1−1(1)(0.8)^3\\ &=1–0.512\\ &=0.488 \end{align}
In such a situation where three crimes happen, what is the expected value and standard deviation of crimes that remain unsolved? Here we apply the formulas for expected value and standard deviation of a binomial.
\begin{align} \mu &=E(X)\\ &=3(0.8)\\ &=2.4 \end{align} \begin{align} \text{Var}(X)&=3(0.8)(0.2)=0.48\\ \text{SD}(X)&=\sqrt{0.48}\approx 0.6928 \end{align}
Note: X can only take values 0, 1, 2, ..., n, but the expected value (mean) of X may be some value other than those that can be assumed by X.
Example 3-8: Cross-Fertilizing
Cross-fertilizing a red and a white flower produces red flowers 25% of the time. Now we cross-fertilize five pairs of red and white flowers and produce five offspring. Find the probability that there will be no red-flowered plants in the five offspring.
Answer
Y = # of red flowered plants in the five offspring. Here, the number of red-flowered plants has a binomial distribution with \(n = 5, p = 0.25\).
\begin{align} P(Y=0)&=\dfrac{5!}{0!(5−0)!}p^0(1−p)^5\\&=1(0.25)^0(0.75)^5\\&=0.237 \end{align}
Try it!
Refer to example 3-8 to answer the following.
- Find the probability that there will be four or more red-flowered plants.
\begin{align} P(\mbox{Y is 4 or more})&=P(Y=4)+P(Y=5)\\ &=\dfrac{5!}{4!(5-4)!} {p}^4 {(1-p)}^1+\dfrac{5!}{5!(5-5)!} {p}^5 {(1-p)}^0\\ &=5\cdot (0.25)^4 \cdot (0.75)^1+ (0.25)^5\\ &=0.015+0.001\\ &=0.016\\ \end{align}
- Of the five cross-fertilized offspring, how many red-flowered plants do you expect?\begin{align} \mu &=5⋅0.25\\&=1.25 \end{align}
- What is the standard deviation of Y, the number of red-flowered plants in the five cross-fertilized offspring?\begin{align} \sigma&=\sqrt{5\cdot0.25\cdot0.75}\\ &=0.97 \end{align}
3.2.3 - Minitab: Binomial Distributions
3.2.3 - Minitab: Binomial DistributionsMinitab® – Finding Binomial Probabilities using Minitab
Let’s walk through how to calculate the probability of 1 out of 3 crimes being solved in the FBI Crime Survey example.
Recall in that example, \(n=3\), \(p=0.2\).
Using Minitab, calculate \(P(X=1)\):
- From the Minitab menu select Calc > Probability Distributions > Binomial
- A dialog box (below) will appear. Enter 3 into the Number of Trials box and 0.2 into the Event Probability box.
- Choose Probability .
- Choose the Input Constant Box and enter 1.
- Choose OK .
The result should be the same probability of 0.384 we found by hand.
Suppose we want to find \(P(X\le 2)\). We can use Minitab to find this cumulative probability.
- From the Minitab menu select Calc > Probability Distributions > Binomial
- Enter in 3 and 0.2 as above.
- Choose Cumulative Probability .
- Choose Input Constant and enter 2.
- Choose OK .
The result should be \(P(X\le 2)=0.992\).
Note!
Depending on if you have the desktop version or cloud version of MINITAB, you will find minor differences in the order of the steps.
Binomial with Minitab
Suppose X follows a binomial distribution with 𝑛=3 and 𝑝=0.2. Calculate 𝑃(𝑋=1).
Calc > Probability Distributions > Probability Density. Fill the dialog box as shown below.
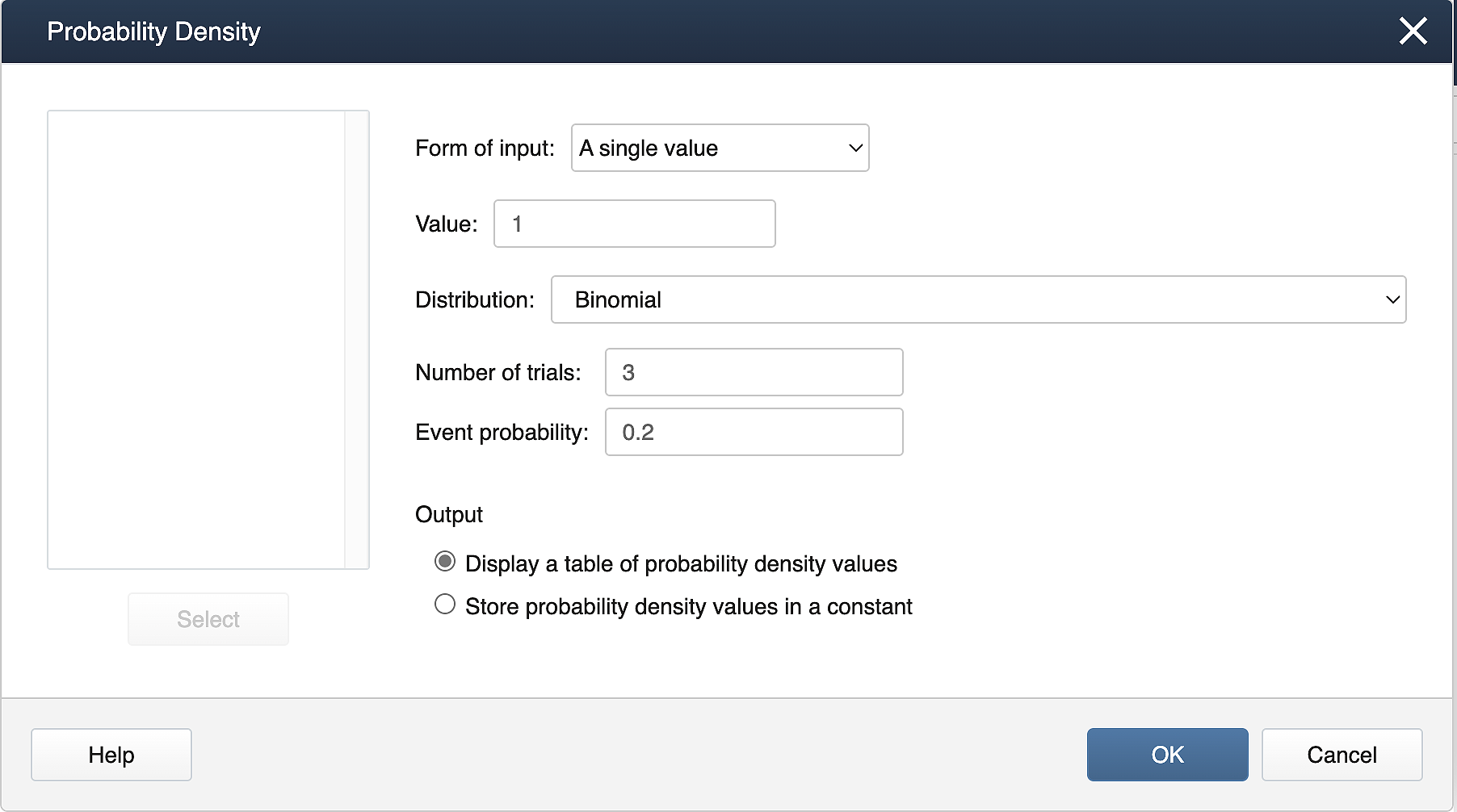
Binomial with n= 3 and p = 0.2
x
P(X=x)
1
0.383
Suppose X follows a binomial distribution with 𝑛=3 and 𝑝=0.2. Calculate P(𝑋≤2).
Calc > Probability Distributions > Cumulative Distribution Function. Fill the dialog box as shown below.
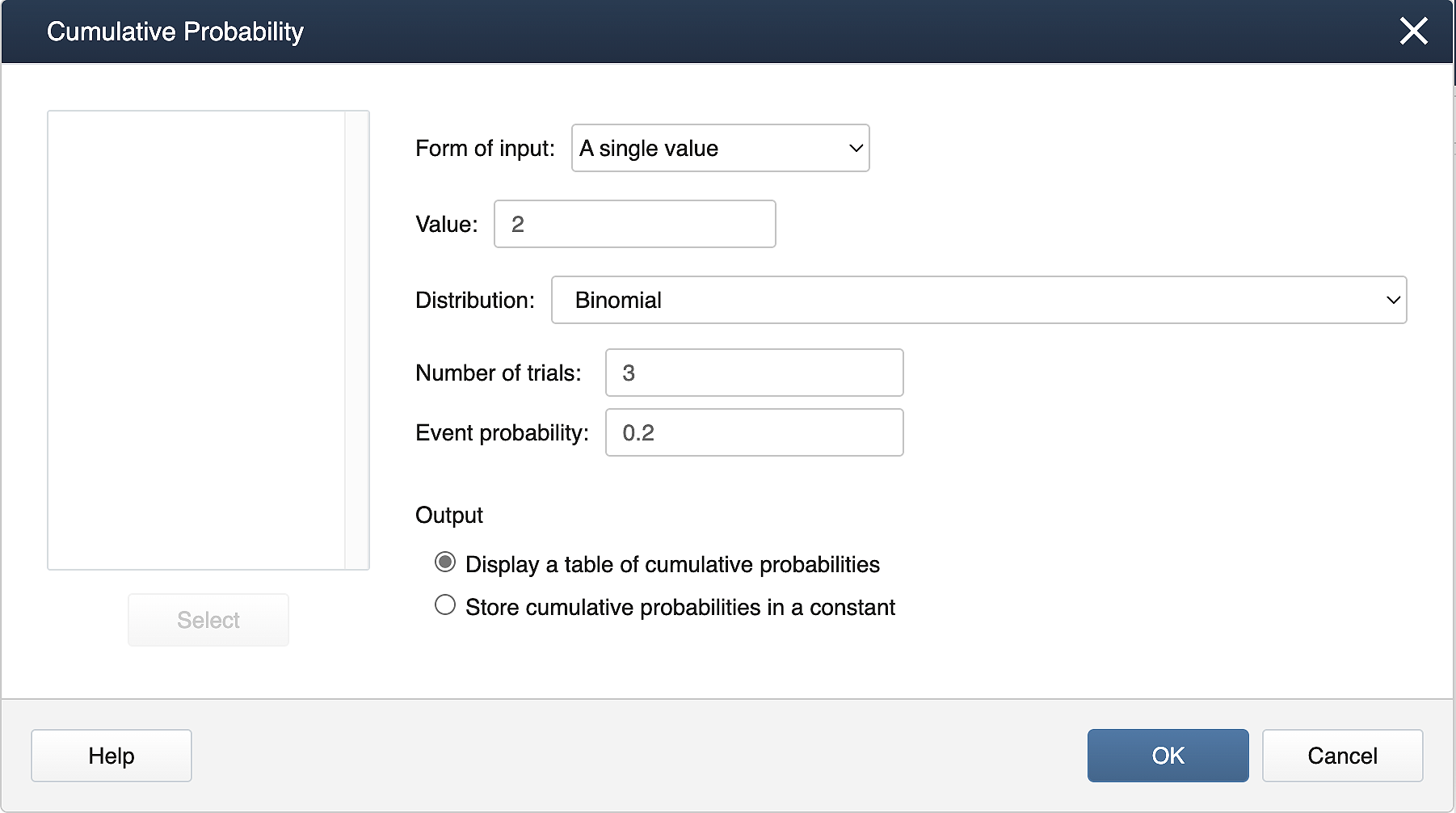
Binomial with n= 3 and p = 0.2
x
P(X≤x)
2
0.992