3.2.3 - Minitab: Binomial Distributions
3.2.3 - Minitab: Binomial DistributionsMinitab® – Finding Binomial Probabilities using Minitab
Let’s walk through how to calculate the probability of 1 out of 3 crimes being solved in the FBI Crime Survey example.
Recall in that example, \(n=3\), \(p=0.2\).
Using Minitab, calculate \(P(X=1)\):
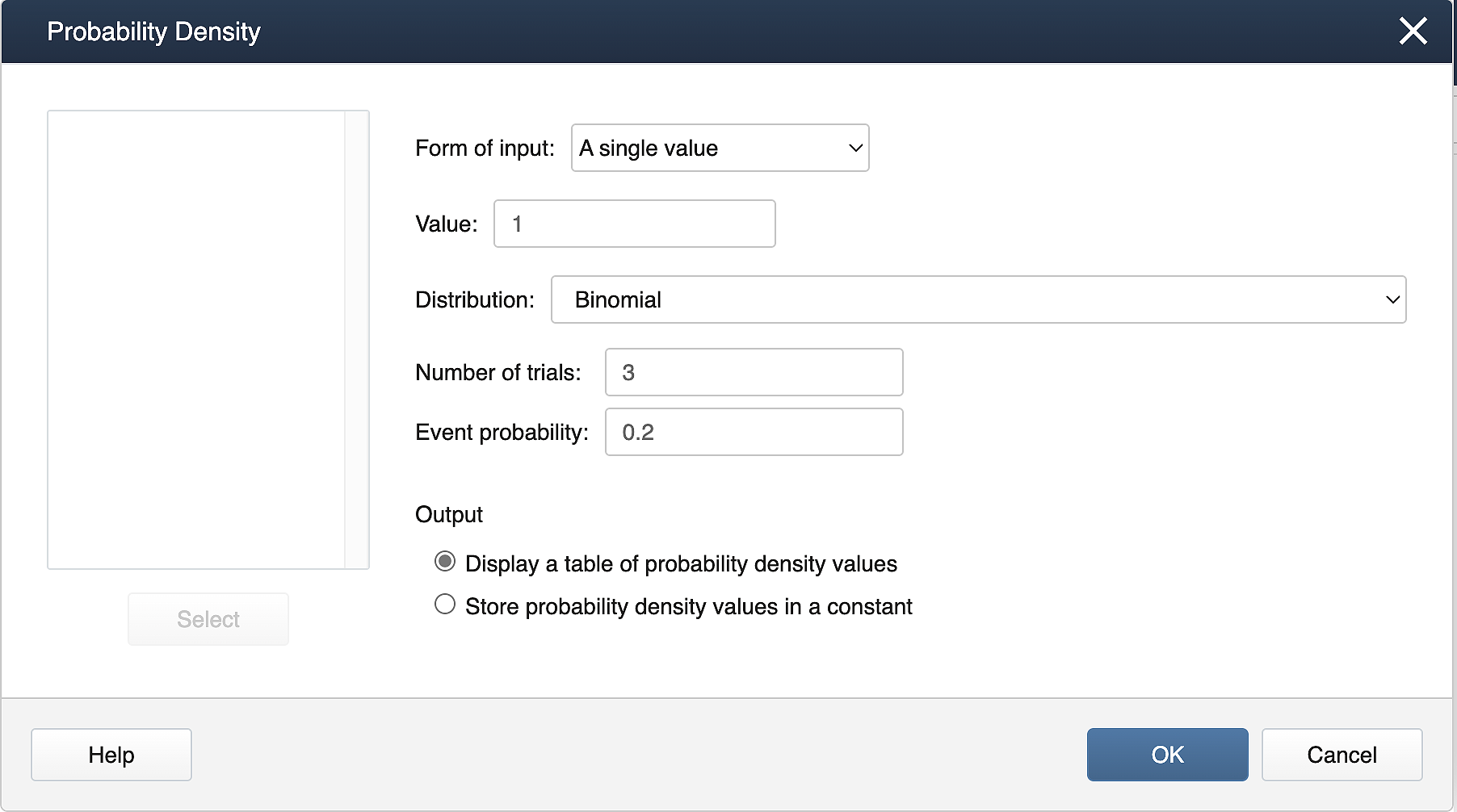
- From the Minitab menu select Calc > Probability Distributions > Binomial
- A dialog box (below) will appear. Enter 3 into the Number of Trials box and 0.2 into the Event Probability box.
- Choose Probability .
- Choose the Input Constant Box and enter 1.
- Choose OK .
The result should be the same probability of 0.384 we found by hand.
Suppose we want to find \(P(X\le 2)\). We can use Minitab to find this cumulative probability.
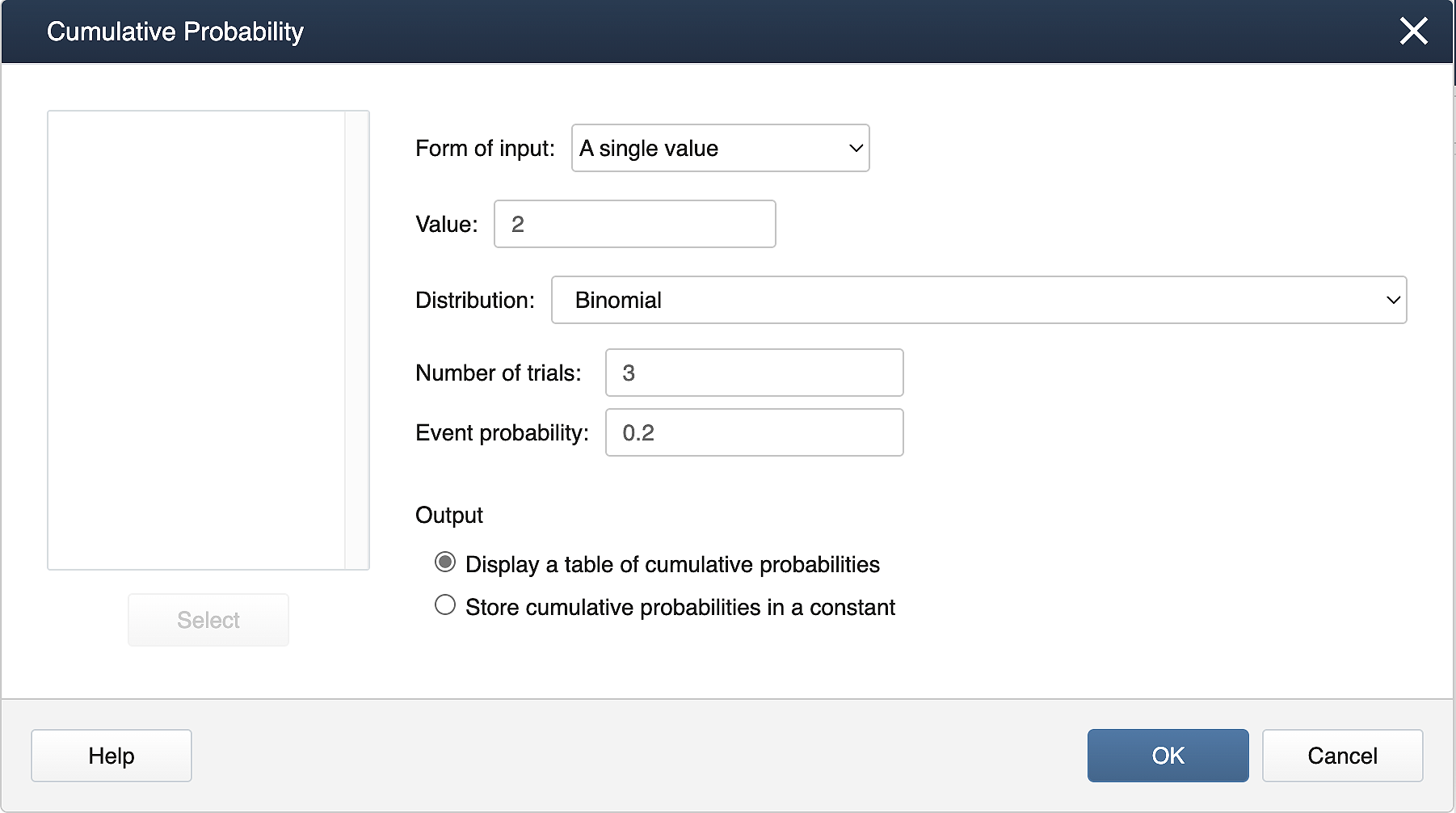
- From the Minitab menu select Calc > Probability Distributions > Binomial
- Enter in 3 and 0.2 as above.
- Choose Cumulative Probability .
- Choose Input Constant and enter 2.
- Choose OK .
The result should be \(P(X\le 2)=0.992\).
Note!
Depending on if you have the desktop version or cloud version of MINITAB, you will find minor differences in the order of the steps.
Binomial with Minitab
Suppose X follows a binomial distribution with 𝑛=3 and 𝑝=0.2. Calculate 𝑃(𝑋=1).
Calc > Probability Distributions > Probability Density. Fill the dialog box as shown below.
Binomial with n= 3 and p = 0.2
x
P(X=x)
1
0.383
Suppose X follows a binomial distribution with 𝑛=3 and 𝑝=0.2. Calculate P(𝑋≤2).
Calc > Probability Distributions > Cumulative Distribution Function. Fill the dialog box as shown below.
Binomial with n= 3 and p = 0.2
x
P(X≤x)
2
0.992