3.3 - Continuous Probability Distributions
3.3 - Continuous Probability DistributionsOverview
In the beginning of the course we looked at the difference between discrete and continuous data. The last section explored working with discrete data, specifically, the distributions of discrete data. In this lesson we're again looking at the distributions but now in terms of continuous data. Examples of continuous data include...
- the amount of rainfall in inches in a year for a city.
- the weight of a newborn baby.
- the height of a randomly selected student.
Properties of Continuous Probability Functions
At the beginning of this lesson, you learned about probability functions for both discrete and continuous data. Recall that if the data is continuous the distribution is modeled using a probability density function ( or PDF).
We define the probability distribution function (PDF) of \(Y\) as \(f(y)\) where: \(P(a < Y < b)\) is the area under \(f(y)\) over the interval from \(a\) to \(b\). (see figure below)
To find probabilities over an interval, such as \(P(a<Y<b)\), using the pdf would require calculus. Instead of doing the calculations by hand, we rely on software and tables to find these probabilities.
Expected value and Variance of a Continuous Random Variable
The expected value and the variance have the same meaning (but different equations) as they did for the discrete random variables.
- Expected Value (or mean) of a Continuous Random Variable
-
The expected value (or mean) of a continuous random variable is denoted by \(\mu=E(Y)\).
- Variance of a Continuous Random Variable
-
The variance of a continuous random variable is denoted by \(\sigma^2=\text{Var}(Y)\).
- Standard Deviation of a Continuous Random Variable
-
The standard deviation of a continuous random variable is denoted by $\sigma=\sqrt{\text{Var}(Y)}$
Notice the equations are not provided for the three parameters above. Therefore, for the continuous case, you will not be asked to find these values by hand.
There are many commonly used continuous distributions. The most important one for this class is the normal distribution. We will describe other distributions briefly.
3.3.1 - The Normal Distribution
3.3.1 - The Normal DistributionThe Normal Distribution is a family of continuous distributions that can model many histograms of real-life data which are mound-shaped (bell-shaped) and symmetric (for example, height, weight, etc.).
A normal curve has two parameters:
- mean $\mu$ (center of the curve)
- standard deviation $\sigma$ (spread about the center) (..and variance $\sigma^2$)
The mean can be any real number and the standard deviation is greater than zero. The normal curve ranges from negative infinity to infinity. The image below shows the effect of the mean and standard deviation on the shape of the normal curve.
3.3.2 - The Standard Normal Distribution
3.3.2 - The Standard Normal DistributionA special case of the normal distribution has mean \(\mu = 0\) and a variance of \(\sigma^2 = 1\). The 'standard normal' is an important distribution.
Standard Normal Distribution
A standard normal distribution has a mean of 0 and variance of 1. This is also known as a z distribution. You may see the notation \(N(\mu, \sigma^2\)) where N signifies that the distribution is normal, \(\mu\) is the mean, and \(\sigma^2\) is the variance. A Z distribution may be described as \(N(0,1)\). Note that since the standard deviation is the square root of the variance then the standard deviation of the standard normal distribution is 1.
Finding Probabilities of a Standard Normal Random Variable
As we mentioned previously, calculus is required to find the probabilities for a Normal random variable. Fortunately, we have tables and software to help us.
For any normal random variable, we can transform it to a standard normal random variable by finding the Z-score. Then we can find the probabilities using the standard normal tables.
Most statistics books provide tables to display the area under a standard normal curve. Look in the appendix of your textbook for the Standard Normal Table. We include a similar table, the Standard Normal Cumulative Probability Table so that you can print and refer to it easily when working on the homework.
Most standard normal tables provide the “less than probabilities”. For example, if \(Z\) is a standard normal random variable, the tables provide \(P(Z\le a)=P(Z<a)\), for a constant, \(a\).
Example 3-9: Probability 'less than'
Find the area under the standard normal curve to the left of 0.87.
There are two main ways statisticians find these numbers that require no calculus! Click on the tabs below to see how to answer using a table and using technology.
A typical four-decimal-place number in the body of the Standard Normal Cumulative Probability Table gives the area under the standard normal curve that lies to the left of a specified z-value. The probability to the left of z = 0.87 is 0.8078 and it can be found by reading the table:
- Since z = 0.87 is positive, use the table for POSITIVE z-values.
- Go down the left-hand column, label z to "0.8."
- Then, go across that row until under the "0.07" in the top row.
You should find the value, 0.8078. Therefore,\(P(Z< 0.87)=P(Z\le 0.87)=0.8078\)
z | .00 | .01 | .02 | .03 | .04 | .05 | .06 | .07 | .08 | .09 |
|---|---|---|---|---|---|---|---|---|---|---|
0.6 | .7257 | .7291 | .7324 | .7357 | .7389 | .7422 | .7454 | .7586 | .7517 | .7549 |
0.7 | .7580 | .7611 | .7642 | .7673 | .7704 | .7734 | .7764 | .7794 | .7823 | .7852 |
0.8 | .7881 | .7910 | .7939 | .7967 | .7995 | .8023 | .8051 | .8078 | .8106 | .8133 |
0.9 | .8159 | .8186 | .8212 | .8238 | .8264 | .8289 | .8315 | .8340 | .8365 | .8389 |
Using Minitab
To find the area to the left of z = 0.87 in Minitab...
- From the Minitab menu select Calc> Probability Distributions> Normal.
- Select Cumulative Probability.
- In the Input constant box, enter 0.87. Click OK
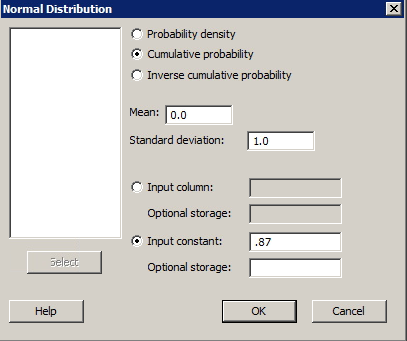
You should see a value very close to 0.8078.
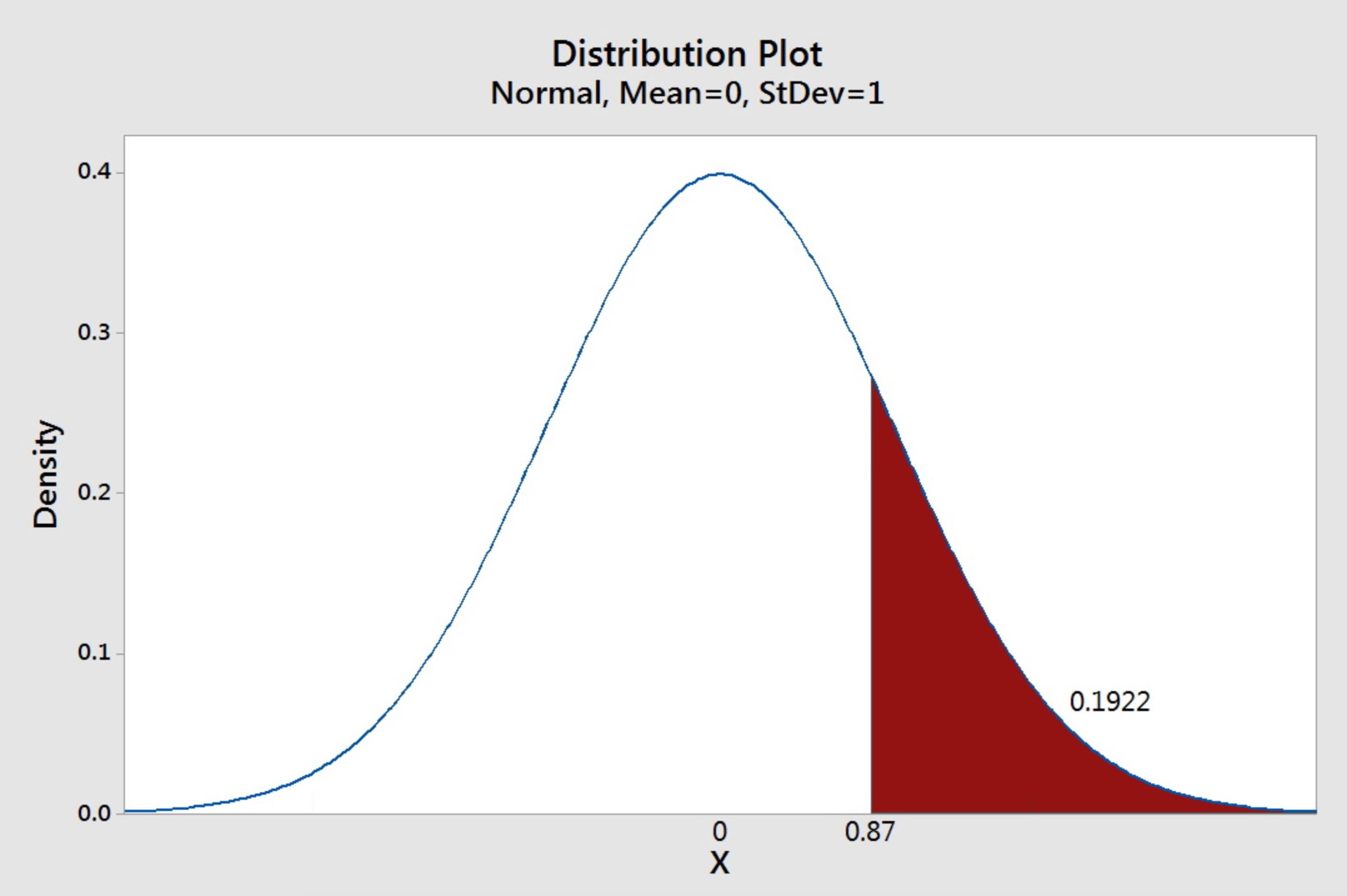
Example 3-10: Probability 'greater than'
Find the area under the standard normal curve to the right of 0.87.
Based on the definition of the probability density function, we know the area under the whole curve is one. Since we are given the “less than” probabilities in the table, we can use complements to find the “greater than” probabilities. Therefore,
\(P(Z>0.87)=1-P(Z\le 0.87)\).
Using the information from the last example, we have \(P(Z>0.87)=1-P(Z\le 0.87)=1-0.8078=0.1922\)
Using Minitab
Since we are given the “less than” probabilities when using the cumulative probability in Minitab, we can use complements to find the “greater than” probabilities. Therefore,
\(P(Z>0.87)=1-P(Z\le 0.87)\).
Using the information from the last example, we have \(P(Z>0.87)=1-P(Z\le 0.87)=1-0.8078=0.1922\)
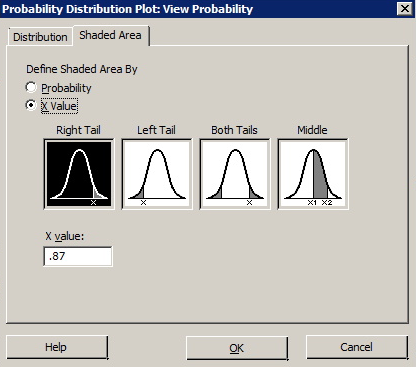
You can also use the probability distribution plots in Minitab to find the "greater than."
- Select Graph> Probability Distribution Plot> View Probability and click OK.
- In the pop-up window select the Normal distribution with a mean of 0.0 and a standard deviation of 1.0.
- Select the Shaded Area tab at the top of the window.
- Select X Value.
- Enter 0.87 for X value.
- Select Right Tail.
- Click OK.
Example 3-11: Probability 'between'
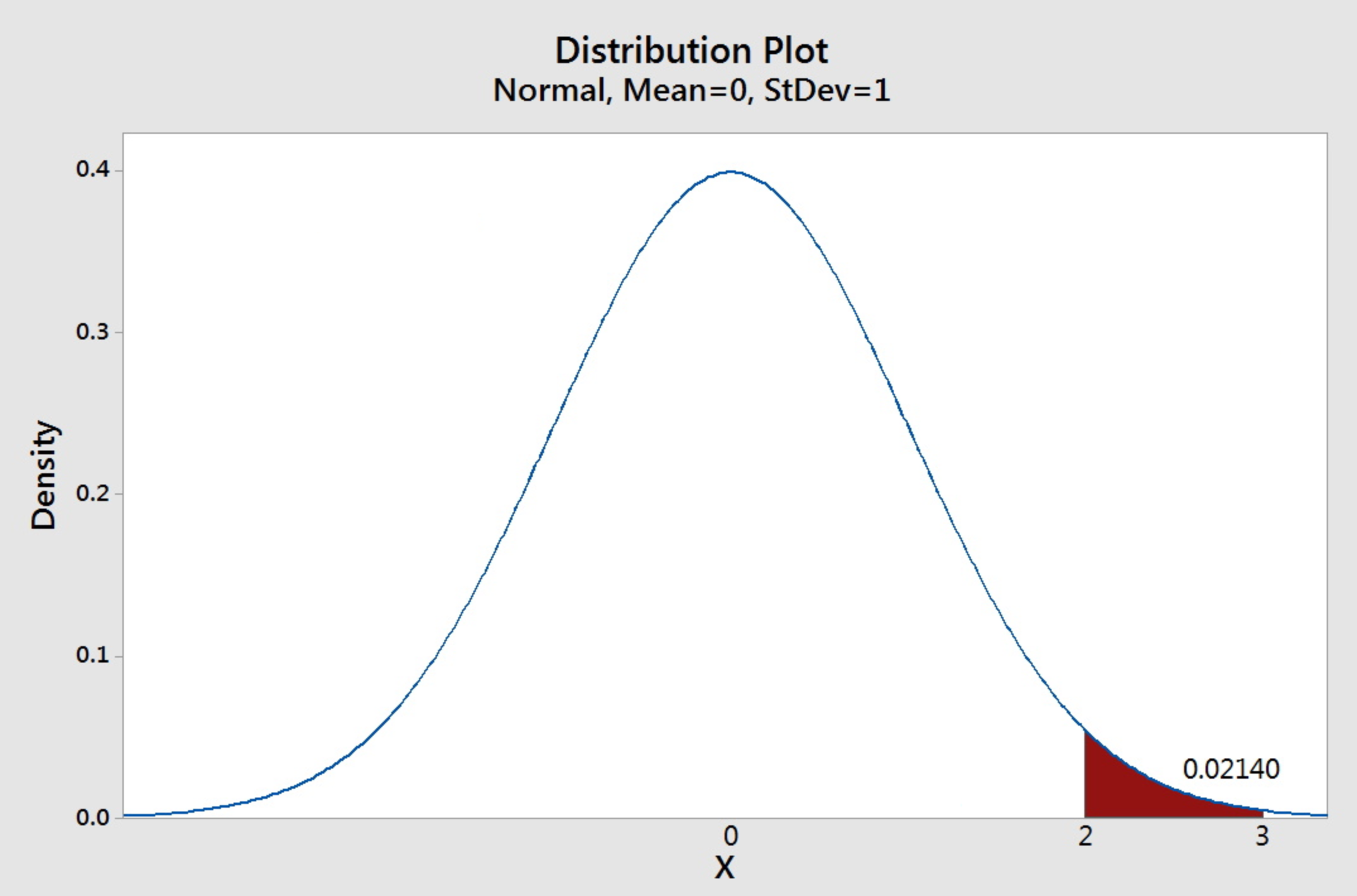
Find the area under the standard normal curve between 2 and 3.
To find the probability between these two values, subtract the probability of less than 2 from the probability of less than 3. In other words,
\(P(2<Z<3)=P(Z<3)-P(Z<2)\)
\(P(Z<3)\) and \(P(Z<2)\) can be found in the table by looking up 2.0 and 3.0.
For 3.0...
z | .00 | .01 | .02 | .03 | .04 | .05 | .06 | .07 | .08 | .09 |
|---|---|---|---|---|---|---|---|---|---|---|
2.8 | 0.9974 | 0.9975 | 0.9976 | 0.9977 | 0.9977 | 0.9978 | 0.9979 | 0.9979 | 0.9980 | 0.9980 |
2.9 | 0.9981 | 0.9982 | 0.9982 | 0.9983 | 0.9984 | 0.9984 | 0.9985 | 0.9985 | 0.9986 | 0.9986 |
3.0 | 0.9987 | 0.9987 | 0.9987 | 0.9988 | 0.9988 | 0.9989 | 0.9989 | 0.9989 | 0.9990 | 0.9990 |
3.1 | 0.9990 | 0.9991 | 0.9991 | 0.9991 | 0.9992 | 0.9992 | 0.9992 | 0.9992 | 0.9993 | 0.9993 |
For 2.0...
z | .00 | .01 | .02 | .03 | .04 | .05 | .06 | .07 | .08 | .09 |
|---|---|---|---|---|---|---|---|---|---|---|
1.8 | 0.9641 | 0.9649 | 0.9656 | 0.9664 | 0.9671 | 0.9678 | 0.9686 | 0.9693 | 0.9699 | 0.9706 |
1.9 | 0.9713 | 0.9719 | 0.9726 | 0.9732 | 0.9738 | 0.9744 | 0.9750 | 0.9756 | 0.9761 | 0.9767 |
2.0 | 0.9772 | 0.9778 | 0.9783 | 0.9788 | 0.9793 | 0.9798 | 0.9803 | 0.9808 | 0.9812 | 0.9817 |
2.1 | 0.9821 | 0.9826 | 0.9830 | 0.9834 | 0.9838 | 0.9842 | 0.9846 | 0.9850 | 0.9854 | 0.9857 |
\(P(2 < Z < 3)= P(Z < 3) - P(Z \le 2)= 0.9987 - 0.9772= 0.0215\).
Using Minitab
To find the area between 2.0 and 3.0 we can use the calculation method in the previous examples to find the cumulative probabilities for 2.0 and 3.0 and then subtract.
\(P(2 < Z < 3)= P(Z < 3) - P(Z \le 2)= 0.9987 - 0.9772= 0.0215\)
You can also use the probability distribution plots in Minitab to find the "between."
- Select Graph> Probability Distribution Plot> View Probability and click OK.
- In the pop-up window select the Normal distribution with a mean of 0.0 and a standard deviation of 1.0.
- Select the Shaded Area tab at the top of the window.
- Select X Value.
- Select Middle.
- Enter 2.0 for X value 1 and 3.0 for X value 2.
- Click OK.
Percentiles of the Standard Normal Distribution
Recall from Lesson 1 that the \(p(100\%)^{th}\) percentile is the value that is greater than \(p(100\%)\) of the values in a data set. We can use the standard normal table and software to find percentiles for the standard normal distribution.
The intersection of the columns and rows in the table gives the probability. If we look for a particular probability in the table, we could then find its corresponding Z value.
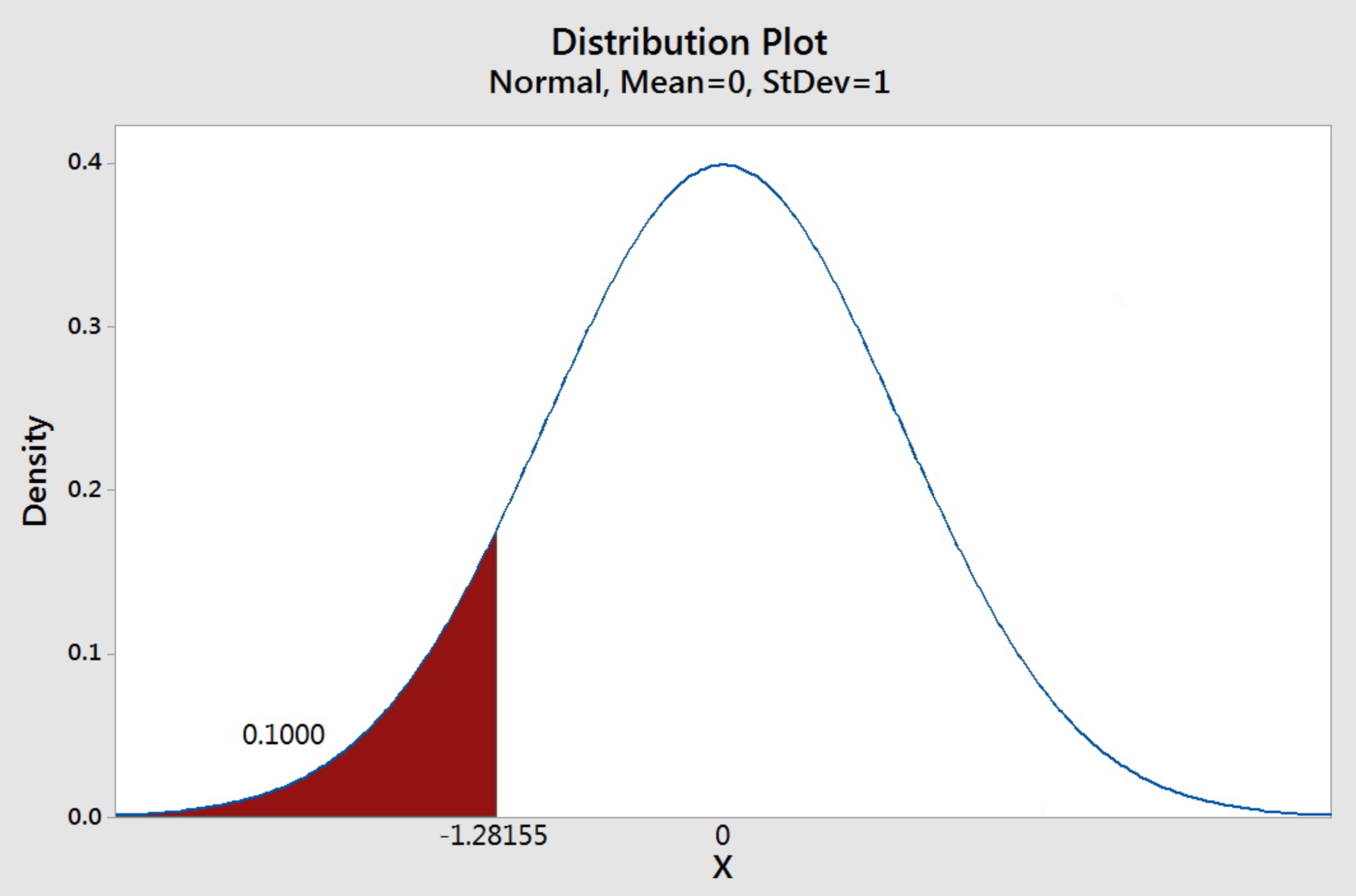
Example 3-12: Percentiles in the Standard Normal Distribution
Find the 10th percentile of the standard normal curve.
The question is asking for a value to the left of which has an area of 0.1 under the standard normal curve.
Since the entries in the Standard Normal Cumulative Probability Table represent the probabilities and they are four-decimal-place numbers, we shall write 0.1 as 0.1000 to remind ourselves that it corresponds to the inside entry of the table. We search the body of the tables and find that the closest value to 0.1000 is 0.1003. We look to the leftmost of the row and up to the top of the column to find the corresponding z-value.
The corresponding z-value is -1.28. Thus z = -1.28.
z | .00 | .01 | .02 | .03 | .04 | .05 | .06 | .07 | .08 | .09 |
|---|---|---|---|---|---|---|---|---|---|---|
-1.3 | 0.0968 | 0.0951 | 0.934 | 0.0918 | 0.0901 | 0.0885 | 0.0869 | 0.0853 | 0.0838 | 0.0823 |
-1.2 | 0.1150 | 0.1131 | 0.1112 | 0.1093 | 0.1075 | 0.1056 | 0.1038 | 0.1020 | 0.1003 | 00985 |
-1.1 | 0.1357 | 0.1335 | 0.1314 | 0.1292 | 0.1271 | 0.1251 | 0.1230 | 0.1210 | 0.1190 | 0.1170 |
-1.0 | 0.1587 | 0.1562 | 0.1539 | 0.1515 | 0.1492 | 0.1469 | 0.1446 | 0.1423 | 0.1401 | 0.1379 |
Therefore, the 10th percentile of the standard normal distribution is -1.28.
Using Minitab
To find the 10th percentile of the standard normal distribution in Minitab...
- Select Calc> Probability Distributions> Normal.
- In the new window choose Inverse Cumulative Probability.
- Enter 0.1 in the Input constant box.
- Click OK.
You should see a value very close to -1.28.
Minitab® – Normal Distribution with Minitab
Consider an alternative approach to calculate cumulative probabilities and normal percentiles in Minitab. Additionally, find the instructions for the same computations using the standard normal table for comparison.
Cumulative Probability
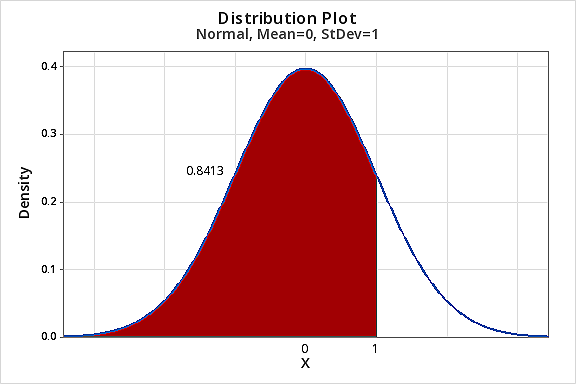
Suppose X has a Normal distribution with mean=10 and variance=4, and we want to find a Cumulative Probability: For example, find \(P(X≤12)\):
\(P(X≤12)=P(Z≤\dfrac{12-10}{\sqrt{4}})=P(Z≤1)=0.8413\)
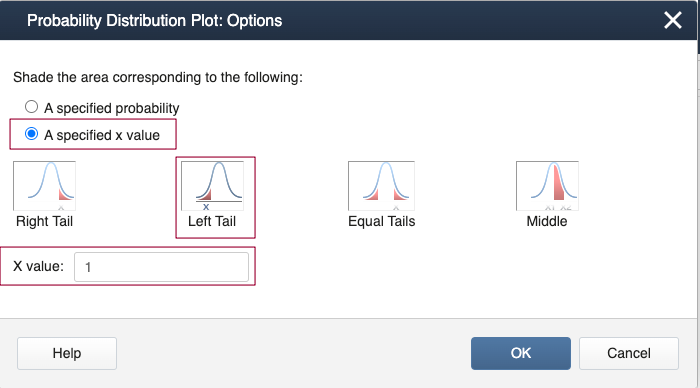
Minitab Method 1 [Graph]:
- Select Graph > Probability Distribution Plot>View Probability > Normal (set the mean = 0 and variance = 1).
- In Options, select 'A specified value', 'Left Tail', and X-value: 1
- Select OKand OK
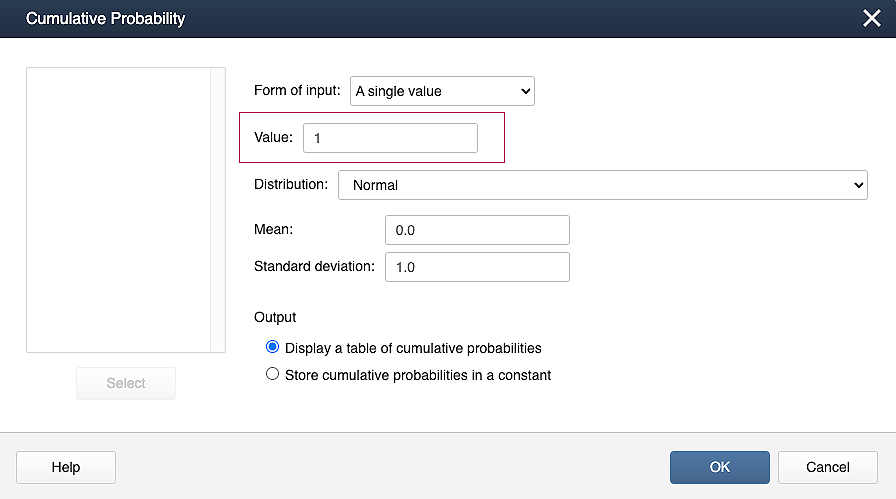
Minitab Method 2 [Calc]:
- Select Calc > Probability Distributions>Cumulative Distribution Function...
- Select 'A single value', Value = 1, Distribution = Normal, Mean = 0 and Standard deviation = 1.
- Select OK
Binomial with n= 3 and p = 0.2
|
x |
P(X≤x) |
|---|---|
|
1 |
0.841345 |
You can read the z-score from the table only to two decimal places. Read up to 1st decimal in the 1st column and the second decimal from the corresponding column as shown below.
|
z |
.00 |
.01 |
.02 |
.03 |
.04 |
.05 |
.06 |
|---|---|---|---|---|---|---|---|
|
0.6 |
.7257 |
.7291 |
.7324 |
.7357 |
.7389 |
.7422 |
.7454 |
|
0.7 |
.7580 |
.7611 |
.7642 |
.7673 |
.7704 |
.7734 |
.7764 |
|
0.8 |
.7881 |
.7910 |
.7939 |
.7967 |
.7995 |
.8023 |
.8051 |
|
0.9 |
.8159 |
.8186 |
.8212 |
.8238 |
.8264 |
.8289 |
.8315 |
|
1.0 |
.8413 |
.8438 |
.8461 |
.8485 |
.8508 |
.8531 |
.8554 |
Therefore, the probability below a Z score of 1 is 0.8413.
Inverse Cumulative Probability
For example, say we want to find the 10th percentile of a normal distribution with a mean = 10 and a variance = 4.
Step 1:
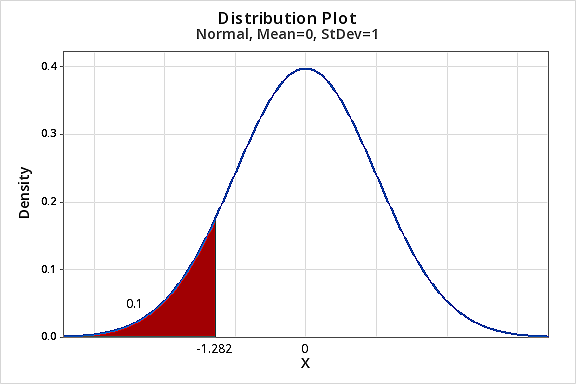
Find the 10th percentile for a standard normal distribution.
That is \(z^*\) find such that \(P(Z≤z^*)=0.10\)→\(z^*=-1.282\)
Minitab Method 1 [Graph]:
- Select Graph > Probability Distribution Plot>View Probability > Normal (set the mean = 0 and variance = 1).
- In Options, select 'A specified value', 'Left Tail', and X-value: 1
- Select OK and OK
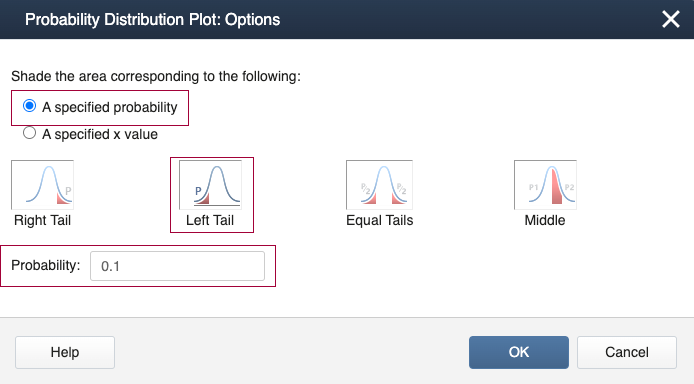
Minitab Method 2 [Calc]:
- Select Calc > Probability Distributions> Inverse Cumulative Distribution Function...
- Select 'A single value', Value = 1, Distribution = Normal, Mean = 0 and Standard deviation = 1.
- Select OK

Normal with mean = 0 and standard deviation = 1
|
x |
P(X≤x) |
|---|---|
|
0.1 |
-1.28155 |
Remember inside the table you have cumulative probabilities. So, you have to look for 0.1 cumulative probability in the table. Since the exact value is not in the table you read the closest value which is 0.1003. Now go to the margins to read the relevant z-score as shown below.
|
z |
.00 |
.01 |
.02 |
.03 |
.04 |
.05 |
.06 |
.07 |
.08 |
.09 |
|---|---|---|---|---|---|---|---|---|---|---|
|
-1.3 |
0.0968 |
0.0951 |
0.934 |
0.0918 |
0.0901 |
0.0885 |
0.0869 |
0.0853 |
0.0838 |
0.0823 |
|
-1.2 |
0.1150 |
0.1131 |
0.1112 |
0.1093 |
0.1075 |
0.1056 |
0.1038 |
0.1020 |
0.1003 |
00985 |
|
-1.1 |
0.1357 |
0.1335 |
0.1314 |
0.1292 |
0.1271 |
0.1251 |
0.1230 |
0.1210 |
0.1190 |
0.1170 |
|
-1.0 |
0.1587 |
0.1562 |
0.1539 |
0.1515 |
0.1492 |
0.1469 |
0.1446 |
0.1423 |
0.1401 |
0.1379 |
Step 2:
Back transform to the original scale.
Now that we have the z-score back transform as below:
\(x^*=10-1.28×2=10-2.56=7.44\)
3.3.3 - Probabilities for Normal Random Variables (Z-scores)
3.3.3 - Probabilities for Normal Random Variables (Z-scores)The standard normal is important because we can use it to find probabilities for a normal random variable with any mean and any standard deviation.
But first, we need to explain Z-scores.
Z-value, Z-score, or Z
We can convert any normal distribution into the standard normal distribution in order to find probability and apply the properties of the standard normal. In order to do this, we use the z-value.
- Z-value, Z-score, or Z
-
The Z-value (or sometimes referred to as Z-score or simply Z) represents the number of standard deviations an observation is from the mean for a set of data. To find the z-score for a particular observation we apply the following formula:
-
\(Z = \dfrac{(observed\ value\ - mean)}{SD}\)
-
Let's take a look at the idea of a z-score within context.
For a recent final exam in STAT 500, the mean was 68.55 with a standard deviation of 15.45.
- If you scored an 80%: \(Z = \dfrac{(80 - 68.55)}{15.45} = 0.74\), which means your score of 80 was 0.74 SD above the mean.
- If you scored a 60%: \(Z = \dfrac{(60 - 68.55)}{15.45} = -0.55\), which means your score of 60 was 0.55 SD below the mean.
Is it always good to have a positive Z score? It depends on the question. For exams, you would want a positive Z-score (indicates you scored higher than the mean). However, if one was analyzing days of missed work then a negative Z-score would be more appealing as it would indicate the person missed less than the mean number of days.
- The scores can be positive or negative.
- For data that is symmetric (i.e. bell-shaped) or nearly symmetric, a common application of Z-scores for identifying potential outliers is for any Z-scores that are beyond ± 3.
- Maximum possible Z-score for a set of data is \(\dfrac{(n−1)}{\sqrt{n}}\)
From Z-score to Probability
For any normal random variable, if you find the Z-score for a value (i.e standardize the value), the random variable is transformed into a standard normal and you can find probabilities using the standard normal table.
For instance, assume U.S. adult heights and weights are both normally distributed. Clearly, they would have different means and standard deviations. However, if you knew these means and standard deviations, you could find your z-score for your weight and height.
You can now use the Standard Normal Table to find the probability, say, of a randomly selected U.S. adult weighing less than you or taller than you.
Example 3-13: Heights
According to the Center for Disease Control, heights for U.S. adult females and males are approximately normal.
- Females: mean of 64 inches and SD of 2 inches
- Males: mean of 69 inches and SD of 3 inches
Find the probability of a randomly selected U.S. adult female being shorter than 65 inches.
Answer
This is asking us to find \(P(X < 65)\). Using the formula \(z=\dfrac{x-\mu}{\sigma}\) we find that:
\(z=\dfrac{65-64}{2}=0.5\)
Now, we have transformed \(P(X < 65)\) to \(P(Z < 0.50)\), where \(Z\) is a standard normal. From the table we see that \(P(Z < 0.50) = 0.6915\). So, roughly there this a 69% chance that a randomly selected U.S. adult female would be shorter than 65 inches.
Example 3-14: Weights
The weights of 10-year-old girls are known to be normally distributed with a mean of 70 pounds and a standard deviation of 13 pounds. Find the percentage of 10-year-old girls with weights between 60 and 90 pounds.
In other words, we want to find \(P(60 < X < 90)\), where \(X\) has a normal distribution with mean 70 and standard deviation 13.
Answer
It is often helpful to draw a sketch of the normal curve and shade in the region of interest. You can either sketch it by hand or use a graphing tool.
To find the probability, we need to first find the Z-scores: \(z=\dfrac{x-\mu}{\sigma}\)
For \(x=60\), we get \(z=\dfrac{60-70}{13}=-0.77\)
For \(x=90\), we get \(z=\dfrac{90-70}{13}=1.54\)
\begin{align*}
P(60<X<90) &= P(-0.77<Z<1.54) &&\text{(Subbing in the Z values from above)} \\
&= P(Z<1.54) - P(Z<-0.77) &&\text{(Subtract the cumulative probabilities)}\\
&=0.9382-0.2206 &&\text{(Use a table or technology)}\\ &=0.7176 \end{align*}
We obtain that 71.76% of 10-year-old girls have weight between 60 pounds and 90 pounds.
Example 3-15: Weights Cont'd...
Find the 60th percentile for the weight of 10-year-old girls given that the weight is normally distributed with a mean 70 pounds and a standard deviation of 13 pounds.
Answer
As before, it is helpful to draw a sketch of the normal curve and shade in the region of interest. You can either sketch it by hand or use a graphing tool. You know that 60% will greater than half of the entire curve.
We can use the Standard Normal Cumulative Probability Table to find the z-scores given the probability as we did before.
Area to the left of z-scores = 0.6000.
The closest value in the table is 0.5987.
The z-score corresponding to 0.5987 is 0.25.
Thus, the 60th percentile is z = 0.25.
Now that we found the z-score, we can use the formula to find the value of \(x\). The Z-score formula is \(z=\dfrac{x-\mu}{\sigma}\).
Using algebra, we can solve for \(x\).
\(x=\mu+z(\sigma)\)
\(x=70+(0.25)(13)=73.25\)
Therefore, the 60th percentile of 10-year-old girls' weight is 73.25 pounds.
3.3.4 - The Empirical Rule
3.3.4 - The Empirical RuleThe Empirical Rule is sometimes referred to as the 68-95-99.7% Rule. The rule is a statement about normal or bell-shaped distributions.
- Empirical Rule
-
In any normal or bell-shaped distribution, roughly...
- 68% of the observations lie within one standard deviation to either side of the mean.
- 95% of the observations lie within two standard deviations to either side of the mean.
- 99.7% of the observations lie within three standard deviations to either side of the mean.
The normal curve showing the empirical rule.
Try It!
Use the normal table to validate the empirical rule. In other words, find the exact probabilities \(P(-1<Z<1)\), \(P(-2<Z<2)\), and \(P(-3<Z<3)\) using the normal table and compare the values to those from the empirical rule.
\(P(-1<Z<1)= P(Z<1)-P(Z<-1) = .8413 - .1587 \approx .68\)
\(P(-2<Z<2)= P(Z<2)-P(Z<-2) = .9772 - .0228 \approx .95\)
\(P(-3<Z<3)= P(Z<3)-P(Z<-3) = .9987 - .0013 \approx .99.7\)
3.3.5 - Other Continuous Distributions
3.3.5 - Other Continuous DistributionsAlthough the normal distribution is important, there are other important distributions of continuous random variables. Some we will introduce throughout the course, but there are many others not discussed. Here are a few distributions that we will see in more detail later.
The t-distribution is a bell-shaped distribution, similar to the normal distribution, but with heavier tails. It is symmetric and centered around zero. The distribution changes based on a parameter called the degrees of freedom. We will discuss degrees of freedom in more detail later.
The graph shows the t-distribution with various degrees of freedom. The standard normal distribution is also shown to give you an idea of how the t-distribution compares to the normal. As you can see, the higher the degrees of freedom, the closer the t-distribution is to the standard normal distribution.
The chi-square distribution is a right-skewed distribution. The distribution depends on the parameter degrees of freedom, similar to the t-distribution. Here is a plot of the Chi-square distribution for various degrees of freedom.
We will see the Chi-square later on in the semester and see how it relates to the Normal distribution.
The F-distribution is a right-skewed distribution. The distribution depends on the two parameters both are referred to as degrees of freedom. The first is typically called the numerator degrees of freedom ($d_1$) and the second is typically referred to as the denominator degrees of freedom ($d_2$). Here is a plot of the F-distribution with various degrees of freedom.
The F-distribution will be discussed in more detail in a future lesson.