4.1.1 - Population is Normal
4.1.1 - Population is NormalIf the population is normally distributed with mean \(\mu\) and standard deviation \(\sigma\), then the sampling distribution of the sample mean is also normally distributed no matter what the sample size is. When the sampling is done with replacement or if the population size is large compared to the sample size, then \(\bar{x}\) has mean \(\mu\) and standard deviation \(\dfrac{\sigma}{\sqrt{n}}\). We use the term standard error for the standard deviation of a statistic, and since sample average, \(\bar{x}\) is a statistic, standard deviation of \(\bar{x}\) is also called standard error of \(\bar{x}\). However, in some books you may find the term standard error for the estimated standard deviation of \(\bar{x}\). In this class we use the former definition, that is, standard error of \(\bar{x}\) is the same as standard deviation of \(\bar{x}\).
- Standard Deviation of \(\boldsymbol{\bar{x}}\) [Standard Error]
- \(SD(\bar{X})=SE(\bar{X})=\dfrac{\sigma}{\sqrt{n}}\)
When we know the sample mean is Normal or approximately Normal, then we can calculate a z-score for the sample mean and determine probabilities for it using:
- Z-Score of the Sample Mean
- \(z=\dfrac{\bar{x}-\mu}{\dfrac{\sigma}{\sqrt{n}}}\)
Example 4-1: Speedboat Engines
The engines made by Ford for speedboats have an average power of 220 horsepower (HP) and standard deviation of 15 HP. You can assume the distribution of power follows a normal distribution.
Consumer Reports® is testing the engines and will dispute the company's claim if the sample mean is less than 215 HP. If they take a sample of 4 engines, what is the probability the mean is less than 215?
Answer
We want to find \(P(\bar{X}<215)\).
Since the population follows a normal distribution, we can conclude that \(\bar{X}\) has a normal distribution with mean 220 HP (\(\mu=220\)) and a standard deviation of \(\dfrac{\sigma}{\sqrt{n}}=\dfrac{15}{\sqrt{4}}=7.5\)HP.
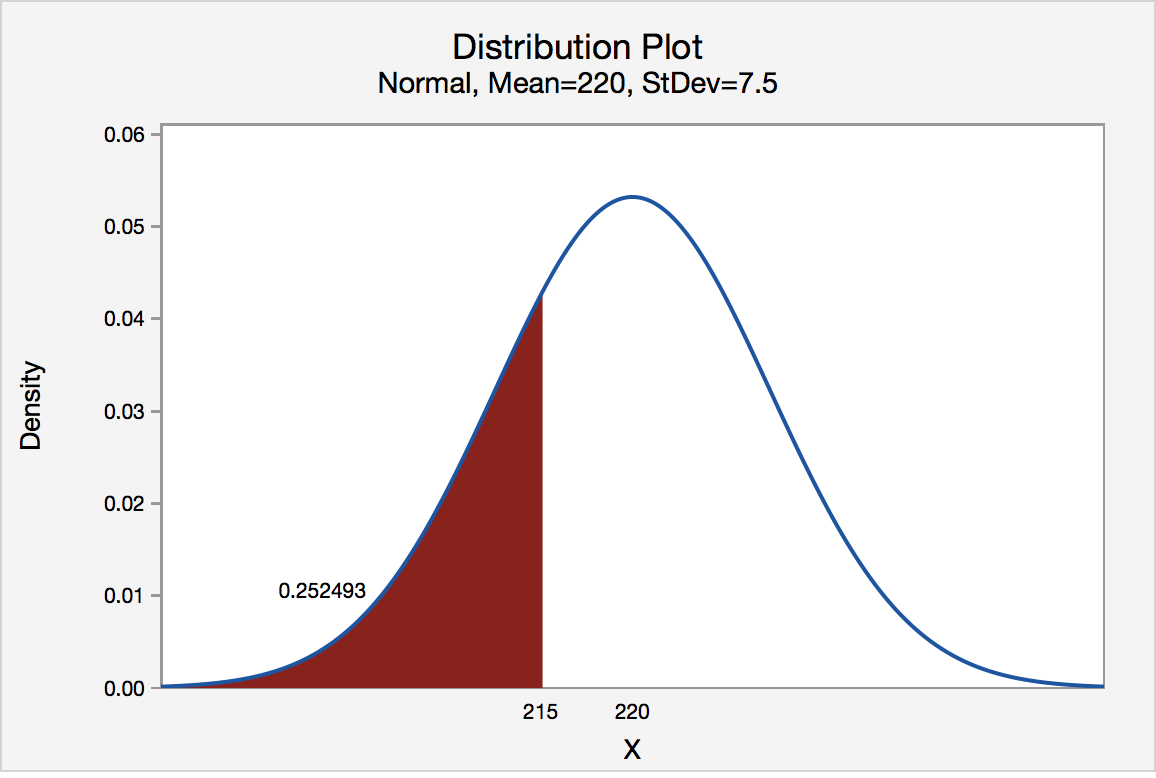
\(P(\bar{X}<215)=P\left(Z<\dfrac{215-220}{7.5}\right)=P(Z<-0.67) \approx\ 0.2514\)
If Consumer Reports® samples four engines, the probability that the mean is less than 215 HP is 25.14%.
Try It!
Using the speedboat engines example above, answer the following question.
If Consumer Reports® samples 100 engines, what is the probability that the sample mean will be less than 215?
The sampling distribution of the sample mean is Normal with mean \(\mu=220\) and standard deviation \(\dfrac{\sigma}{\sqrt{n}}=\dfrac{15}{\sqrt{100}}=1.5\).
\(P(\bar{X}<215)=P\left(\dfrac{\bar{X}-\mu}{\dfrac{\sigma}{\sqrt{n}}}<\dfrac{215-220}{1.5}\right)=P\left(Z<-\dfrac{10}{3}\right)=0.00043\).
It is worth noting the difference in the probabilities here. When the sample size is \(n=4\), the probability of obtaining a sample mean of 215 or less is 25.14%. When the sample size is \(n=100\), the probability is 0.043%.