5.4.2 - The t-distribution

In 1908, William Sealy Gosset from Guinness Breweries discovered the t-distribution. His pen-name was Student and thus it is called the "Student's t-distribution."

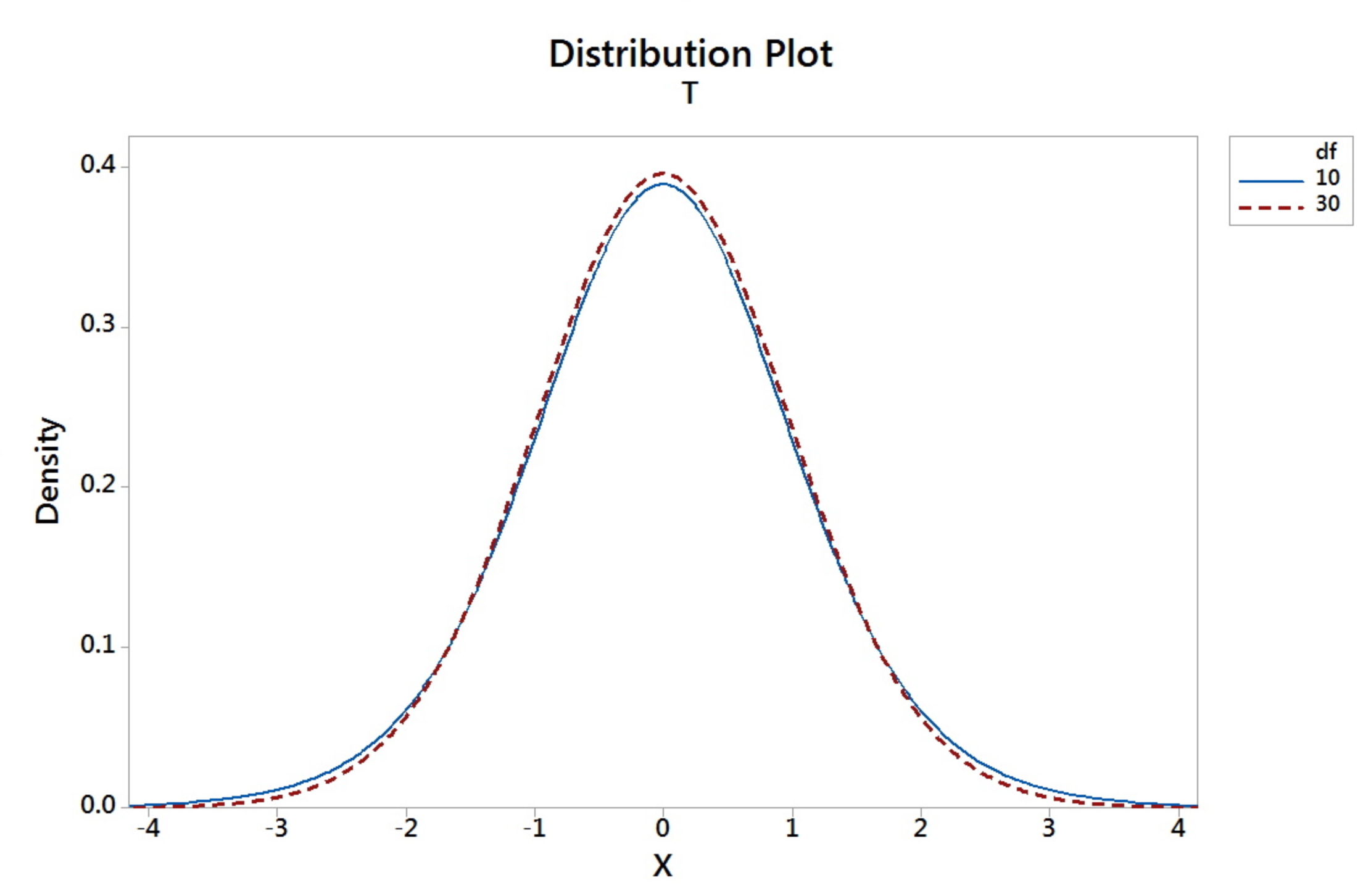
The t-distribution is different for different sample size, n. Thus, tables, as detailed as the standard normal table, are not provided in the usual statistics books. The graph below shows the t-distribution for degrees of freedom of 10 (blue) and 30 (red dashed).

T-distribution graph with degrees freedom fo 10 and 30 — t-distribution

Properties of the t-distribution

t is symmetric about 0
t-distribution is more variable than the Standard Normal distribution
t-distributions are different for different degrees of freedom (d.f.).
The larger $n$ gets (or as $n$ goes to infinity), the closer the $t$-distribution is to the $z$.
The meaning of $t_\alpha$ is the $t$-value having the area "$\alpha$" to the right of it.

Example 5-5: Finding t-values

Use this t-table or the one in your text to find following the example.

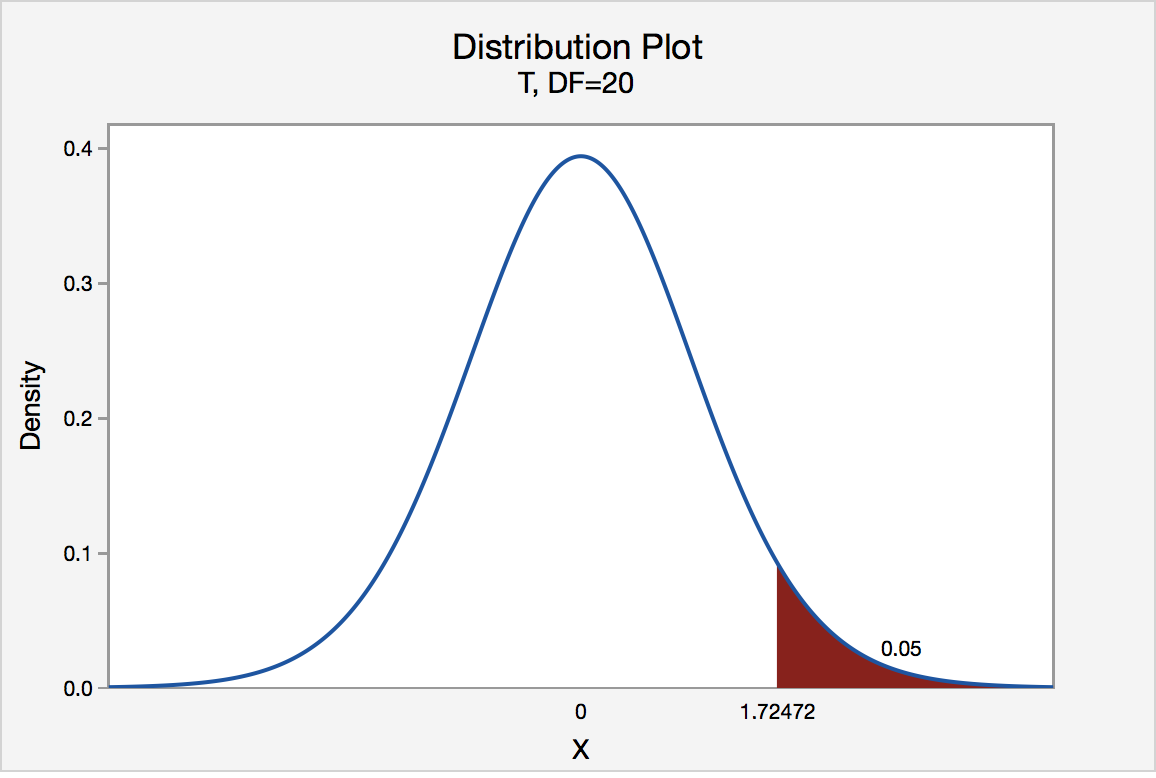
Find $t_{0.05}$ where the degree of freedom is 20.

In a t-distribution table below the top row represents the upper tail area, while the first column are the degrees of freedom.

The $t_{0.05}$ where the degree of freedom is 20 is 1.725 .

df	0.40	0.25	0.10	0.05	0.025	0.01	0.005	0.001	.0005
...	...	...	...	...	...	...	...	...	...
18	0.257	0.688	1.330	1.734	2.101	2.552	2.878	3.610	3.922
19	0.257	0.688	1.328	1.729	2.093	2.539	2.861	3.579	3.883
20	0.257	0.687	1.325	1.725	2.086	2.528	2.845	3.552	3.850
21	0.257	0.686	1.323	1.721	2.080	2.518	2.831	3.527	3.819

The graph shows that the $\alpha$ values at the top of this table are the upper tail areas of the distribution.

t-distribution curve showing a t value of 1.725

Note! When the corresponding degree of freedom is not given in the table, you can use the value for the closest degree of freedom that is smaller than the given one. We use this approach since it is better to err in a conservative manner (get a t-value that is slightly larger than the precise t-value).

Find $t_{0.05}$ where the degree of freedom is 34.

What do we do when the degrees of freedom are not on the table? The t-table degrees of freedom run continuously from 1 to 30, then go by intervals after 30 (e.g. after 30 we have 35). In such cases, we can use software such as Minitab to find a more exact value for the multiplier as opposed to using a degrees of freedom that is "close".

To find the t-value in Minitab...

From the Minitab Menu select Calc > Probability Distributions > t...
Choose inverse cumulative probability
Enter the degrees of freedom
Set the input constant as 0.95 (1 - 0.05).
Choose OK

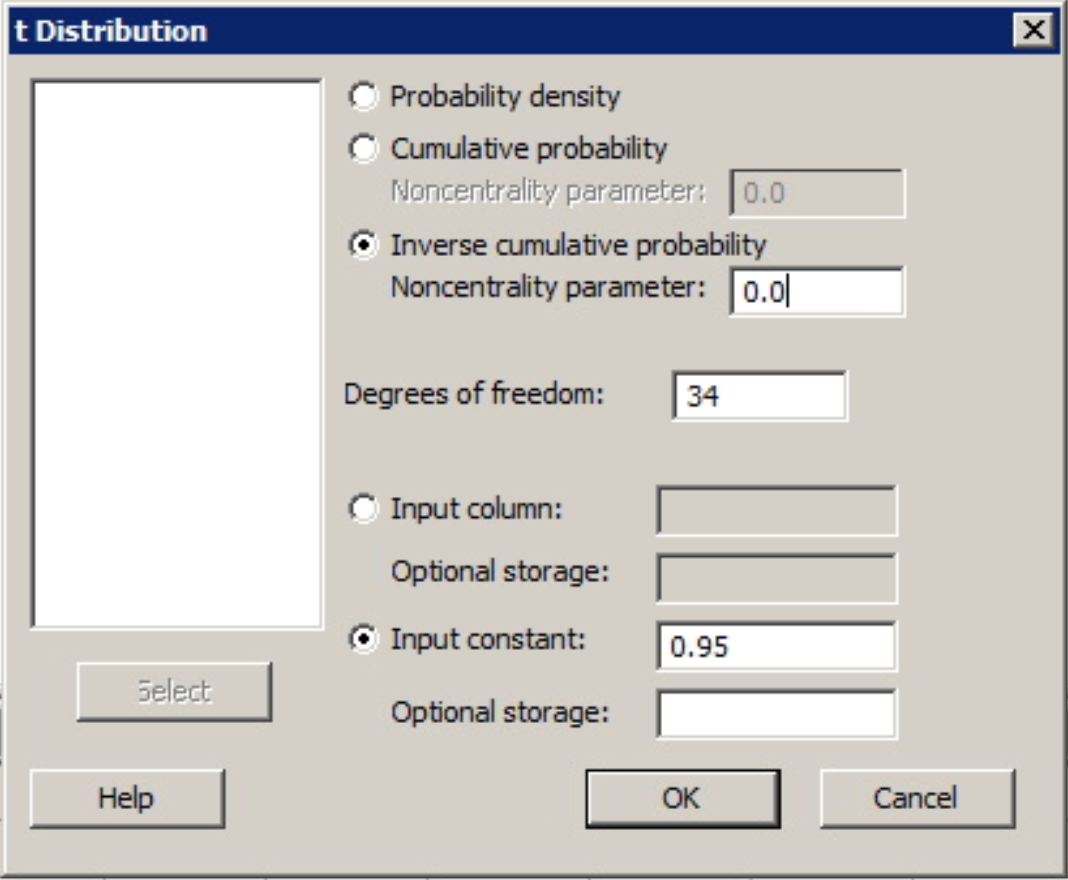
Minitab window for the t -distribution

The output from Minitab gives us $t_{0.05}$ with df= 34 as 1.69092.

P (X $\le$ x)	x
0.95	1.69092

Find $t_{0.05}$ where the degree of freedom is 30.

The t-value for an $\alpha$ of .05 and df of 30 is 1.697.

df	0.40	0.25	0.10	0.05	0.025	0.01	0.005	0.001	.0005
...	...	...	...	...	...	...	...	...	...
27	0.256	0.684	1.314	1.703	2.052	2.473	2.771	3.421	3.690
28	0.256	0.683	1.313	1.701	2.048	2.467	2.763	3.408	3.674
29	0.256	0.683	1.311	1.699	2.045	2.462	2.756	3.396	3.659
30	0.256	0.683	1.310	1.697	2.042	2.457	2.750	3.385	3.646

Note! When the sample size is larger than 30, the t-values are not that different from the z-values. Thus, a crude estimate for $t_{0.05}$ with 34 degrees of freedom is $z_{0.05} = 1.645$. Although it is a crude estimate, when software is available, it is best to find the $t$ values rather than use the $z$.

^[1]	Link
↥	Has Tooltip/Popover
	Toggleable Visibility