T.3.5 - Exponential Regression Example

One simple nonlinear model is the exponential regression model

\(\begin{equation*}
y_{i}=\beta_{0}+\beta_{1}\exp(\beta_{2}x_{i,1}+\ldots+\beta_{p+1}x_{i,1})+\epsilon_{i},
\end{equation*}\)

where the \(\epsilon_{i}\) are iid normal with mean 0 and constant variance \(\sigma^{2}\). Notice that if \(\beta_{0}=0\), then the above is intrinsically linear by taking the natural logarithm of both sides.

Exponential regression is probably one of the simplest nonlinear regression models. An example where an exponential regression is often utilized is when relating the concentration of a substance (the response) to elapsed time (the predictor).

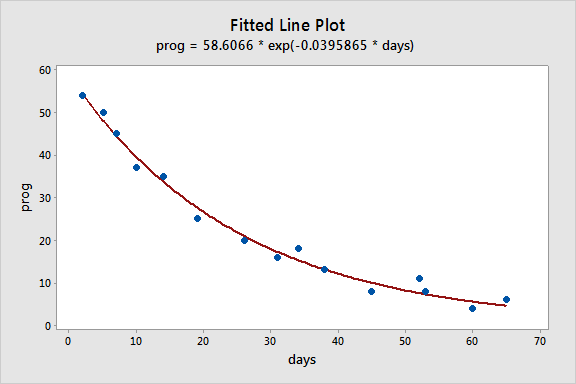
To illustrate, consider the example of long-term recovery after discharge from the hospital from page 514 of Applied Linear Regression Models (4th ed) by Kutner, Nachtsheim, and Neter. The response variable, Y, is the prognostic index for long-term recovery, and the predictor variable, X, is the number of days of hospitalization. The proposed model is the two-parameter exponential model:

\(\begin{equation*}
Y_{i}=\theta_{0}\exp(\theta_{1}X_i)+\epsilon_{i},
\end{equation*}\)

where the \(\epsilon_i\) are independent normal with constant variance.

We'll use Minitab's nonlinear regression routine to apply the Gauss-Newton algorithm to estimate \(\theta_0\) and \(\theta_1\). Before we do this, however, we have to find initial values for \(\theta_0\) and \(\theta_1\). One way to do this is to note that we can linearize the response function by taking the natural logarithm:

\(\begin{equation*}
\log(\theta_{0}\exp(\theta_{1}X_i)) = \log(\theta_{0}) + \theta_{1}X_i.
\end{equation*}\)

Thus we can fit a simple linear regression model with the response, \(\log(Y)\), and predictor, \(X\), and the intercept (\(4.0372\)) give us an estimate of \(\log(\theta_{0})\) while the slope (\(-0.03797\)) gives us an estimate of \(\theta_{1}\). (We then calculate \(\exp(4.0372)=56.7\) to estimate \(\theta_0\).)

 Minitab: Nonlinear Regression Model

Now we can fit the nonlinear regression model:

1. Select Stat > Regression > Nonlinear Regression, select prog for the response, and click "Use Catalog" under "Expectation Function."
2. Select the "Exponential" function with 1 predictor and 2 parameters in the Catalog dialog box and click OK to go to the "Choose Predictors" dialog.
3. Select days to be the "Actual predictor" and click OK to go back to the Catalog dialog box, where you should see "Theta1 * exp( Theta2 * days )" in the "Expectation Function" box.
4. Click "Parameters" and type "56.7" next to "Theta1" and "-0.038" next to "Theta2" and click OK to go back to the Nonlinear Regression dialog box.
5. Click "Options" to confirm that Minitab will use the Gauss-Newton algorithm (the other choice is Levenberg-Marquardt) and click OK to go back to the Nonlinear Regression dialog box.
6. Click "Graphs" to confirm that Minitab will produce a plot of the fitted curve with data and click OK to go back to the Nonlinear Regression dialog box.
7. Click OK to obtain the following output:

Nonlinear Regression: Prog = Theta1 * exp(Theta2 * days)

Method

Algorithm	Gauss-Newton
Max iterations	200
Tolerance	0.00001

Starting Values for Parameters

Parameter	Value
Theta1	56.7
Theta2	-0.038

Equation

prog = 58.6066 * exp(-0.0395865 * days)

Parameter Estimates

Parameter	Estimate	SE Estimate
Theta1	58.6066	1.47216
Theta2	0.0396	0.00171

prog = Theta1 * exp(Theta2 * days)

Summary

Iterations	5
Final SSE	49.4593
DFE	13
MSE	3.80456
S	1.95053