Lesson 13: Weighted Least Squares & Logistic Regressions
Lesson 13: Weighted Least Squares & Logistic RegressionsIn this lesson, we will learn about two important extensions to the standard linear regression model that we have discussed.
In the first part of the lesson, we will discuss the weighted least squares approach which would be useful in estimating regression parameters when heteroscedasticity is present.
In the second part of the lesson, we will turn to a class of regression models that we can use when our response variable is binary.
Lesson 13 Objectives
- Explain the idea behind weighted least squares.
- Apply weighted least squares to regression examples with nonconstant variance.
- Apply logistic regression techniques to datasets with a binary response variable.
13.1 - Weighted Least Squares
13.1 - Weighted Least SquaresThe method of ordinary least squares assumes that there is constant variance in the errors (which is called homoscedasticity). The method of weighted least squares can be used when the ordinary least squares assumption of constant variance in the errors is violated (which is called heteroscedasticity). The model under consideration is
\(\begin{equation*} \textbf{Y}=\textbf{X}\beta+\epsilon^{*}, \end{equation*}\)
where \(\epsilon^{*}\) is assumed to be (multivariate) normally distributed with mean vector 0 and nonconstant variance-covariance matrix
\(\begin{equation*} \left(\begin{array}{cccc} \sigma^{2}_{1} & 0 & \ldots & 0 \\ 0 & \sigma^{2}_{2} & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & \sigma^{2}_{n} \\ \end{array} \right) \end{equation*}\)
If we define the reciprocal of each variance, \(\sigma^{2}_{i}\), as the weight, \(w_i = 1/\sigma^{2}_{i}\), then let matrix W be a diagonal matrix containing these weights:
\(\begin{equation*}\textbf{W}=\left( \begin{array}{cccc} w_{1} & 0 & \ldots & 0 \\ 0& w_{2} & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0& 0 & \ldots & w_{n} \\ \end{array} \right) \end{equation*}\)
The weighted least squares estimate is then
\(\begin{align*} \hat{\beta}_{WLS}&=\arg\min_{\beta}\sum_{i=1}^{n}\epsilon_{i}^{*2}\\ &=(\textbf{X}^{T}\textbf{W}\textbf{X})^{-1}\textbf{X}^{T}\textbf{W}\textbf{Y} \end{align*}\)
With this setting, we can make a few observations:
- Since each weight is inversely proportional to the error variance, it reflects the information in that observation. So, an observation with a small error variance has a large weight since it contains relatively more information than an observation with a large error variance (small weight).
- The weights have to be known (or more usually estimated) up to a proportionality constant.
To illustrate, consider the famous 1877 Galton data set, consisting of 7 measurements each of X = Parent (pea diameter in inches of parent plant) and Y = Progeny (average pea diameter in inches of up to 10 plants grown from seeds of the parent plant). Also included in the dataset are standard deviations, SD, of the offspring peas grown from each parent. These standard deviations reflect the information in the response Y values (remember these are averages) and so in estimating a regression model we should downweight the observations with a large standard deviation and upweight the observations with a small standard deviation. In other words, we should use weighted least squares with weights equal to \(1/SD^{2}\). The resulting fitted equation from Minitab for this model is:
Progeny = 0.12796 + 0.2048 Parent
Compare this with the fitted equation for the ordinary least squares model:
Progeny = 0.12703 + 0.2100 Parent
The equations aren't very different but we can gain some intuition into the effects of using weighted least squares by looking at a scatterplot of the data with the two regression lines superimposed:
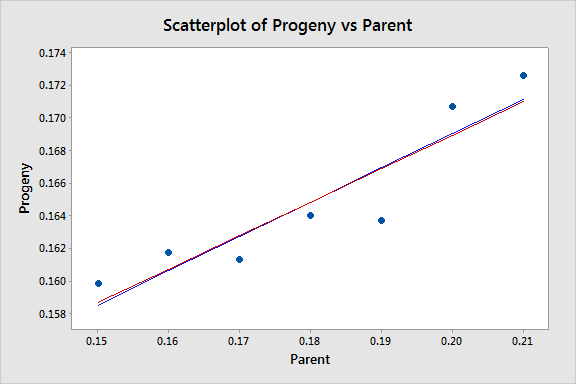
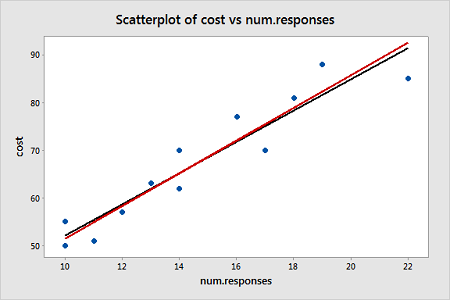
The black line represents the OLS fit, while the red line represents the WLS fit. The standard deviations tend to increase as the value of Parent increases, so the weights tend to decrease as the value of Parent increases. Thus, on the left of the graph where the observations are up-weighted the red fitted line is pulled slightly closer to the data points, whereas on the right of the graph where the observations are down-weighted the red fitted line is slightly further from the data points.
For this example, the weights were known. There are other circumstances where the weights are known:
- If the i-th response is an average of \(n_i\) equally variable observations, then \(Var\left(y_i \right)\) = \(\sigma^2/n_i\) and \(w_i\) = \(n_i\).
- If the i-th response is a total of \(n_i\) observations, then \(Var\left(y_i \right)\) = \(n_i\sigma^2\) and \(w_i\) =1/ \(n_i\).
- If variance is proportional to some predictor \(x_i\), then \(Var\left(y_i \right)\) = \(x_i\sigma^2\) and \(w_i\) =1/ \(x_i\).
In practice, for other types of datasets, the structure of W is usually unknown, so we have to perform an ordinary least squares (OLS) regression first. Provided the regression function is appropriate, the i-th squared residual from the OLS fit is an estimate of \(\sigma_i^2\) and the i-th absolute residual is an estimate of \(\sigma_i\) (which tends to be a more useful estimator in the presence of outliers). The residuals are much too variable to be used directly in estimating the weights, \(w_i,\) so instead we use either the squared residuals to estimate a variance function or the absolute residuals to estimate a standard deviation function. We then use this variance or standard deviation function to estimate the weights.
Some possible variance and standard deviation function estimates include:
- If a residual plot against a predictor exhibits a megaphone shape, then regress the absolute values of the residuals against that predictor. The resulting fitted values of this regression are estimates of \(\sigma_{i}\). (And remember \(w_i = 1/\sigma^{2}_{i}\)).
- If a residual plot against the fitted values exhibits a megaphone shape, then regress the absolute values of the residuals against the fitted values. The resulting fitted values of this regression are estimates of \(\sigma_{i}\).
- If a residual plot of the squared residuals against a predictor exhibits an upward trend, then regress the squared residuals against that predictor. The resulting fitted values of this regression are estimates of \(\sigma_{i}^2\).
- If a residual plot of the squared residuals against the fitted values exhibits an upward trend, then regress the squared residuals against the fitted values. The resulting fitted values of this regression are estimates of \(\sigma_{i}^2\).
After using one of these methods to estimate the weights, \(w_i\), we then use these weights in estimating a weighted least squares regression model. We consider some examples of this approach in the next section.
Some key points regarding weighted least squares are:
- The difficulty, in practice, is determining estimates of the error variances (or standard deviations).
- Weighted least squares estimates of the coefficients will usually be nearly the same as the "ordinary" unweighted estimates. In cases where they differ substantially, the procedure can be iterated until estimated coefficients stabilize (often in no more than one or two iterations); this is called iteratively reweighted least squares.
- In some cases, the values of the weights may be based on theory or prior research.
- In designed experiments with large numbers of replicates, weights can be estimated directly from sample variances of the response variable at each combination of predictor variables.
- The use of weights will (legitimately) impact the widths of statistical intervals.
13.1.1 - Weighted Least Squares Examples
13.1.1 - Weighted Least Squares ExamplesExample 13-1: Computer-Assisted Learning Dataset

The Computer-Assisted Learning New data was collected from a study of computer-assisted learning by n = 12 students.
| i | Responses | Cost |
|---|---|---|
| 1 | 16 | 77 |
| 2 | 14 | 70 |
| 3 | 22 | 85 |
| 4 | 10 | 50 |
| 5 | 14 | 62 |
| 6 | 17 | 70 |
| 7 | 10 | 55 |
| 8 | 13 | 63 |
| 9 | 19 | 88 |
| 10 | 12 | 57 |
| 11 | 18 | 81 |
| 12 | 11 | 51 |
The response is the cost of the computer time (Y) and the predictor is the total number of responses in completing a lesson (X). A scatterplot of the data is given below.
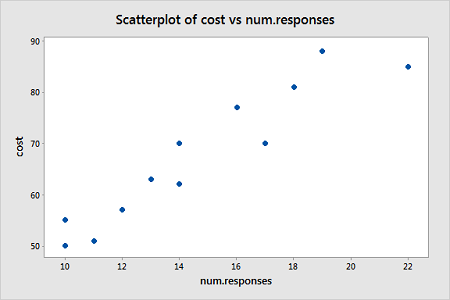
From this scatterplot, a simple linear regression seems appropriate for explaining this relationship.
First, an ordinary least squares line is fit to this data. Below is the summary of the simple linear regression fit for this data
Model Summary
| S | R-sq | R-sq(adj) | R-sq(pred) |
|---|---|---|---|
| 4.59830 | 88.91% | 87.80% | 81.27% |
Coefficients
| Term | Coef | SE Coef | T-Value | P-Value | VIF |
|---|---|---|---|---|---|
| Constant | 19.47 | 5.52 | 3.53 | 0.005 | |
| num.responses | 3.269 | 0.365 | 8.95 | 0.000 | 1.00 |
Regression Equation
cost = 19.47 + 3.269 num.responses
A plot of the residuals versus the predictor values indicates possible nonconstant variance since there is a very slight "megaphone" pattern:
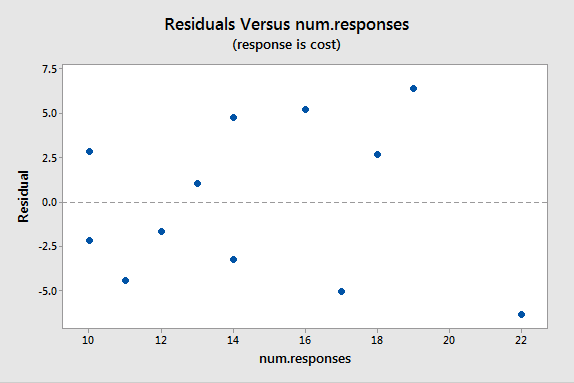
We will turn to weighted least squares to address this possibility. The weights we will use will be based on regressing the absolute residuals versus the predictor. In Minitab, we can use the Storage button in the Regression Dialog to store the residuals. Then we can use Calc > Calculator to calculate the absolute residuals. A plot of the absolute residuals versus the predictor values is as follows:
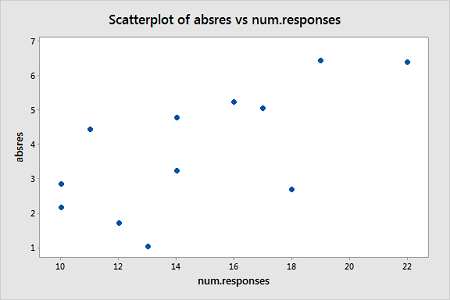
The weights we will use will be based on regressing the absolute residuals versus the predictor. Specifically, we will fit this model, use the Storage button to store the fitted values, and then use Calc > Calculator to define the weights as 1 over the squared fitted values. Then we fit a weighted least squares regression model by fitting a linear regression model in the usual way but clicking "Options" in the Regression Dialog and selecting the just-created weights as "Weights."
The summary of this weighted least squares fit is as follows:
Model Summary
| S | R-sq | R-sq(adj) | R-sq(pred) |
|---|---|---|---|
| 1.15935 | 89.51% | 88.46% | 83.87% |
Coefficients
| Term | Coef | SE Coef | T-Value | P-Value | VIF |
|---|---|---|---|---|---|
| Constant | 17.30 | 4.83 | 3.58 | 0.005 | |
| num.responses | 3.421 | 0.370 | 9.24 | 0.000 | 1.00 |
Notice that the regression estimates have not changed much from the ordinary least squares method. The following plot shows both the OLS fitted line (black) and WLS fitted line (red) overlaid on the same scatterplot.
A plot of the studentized residuals (remember Minitab calls these "standardized" residuals) versus the predictor values when using the weighted least squares method shows how we have corrected for the megaphone shape since the studentized residuals appear to be more randomly scattered about 0:
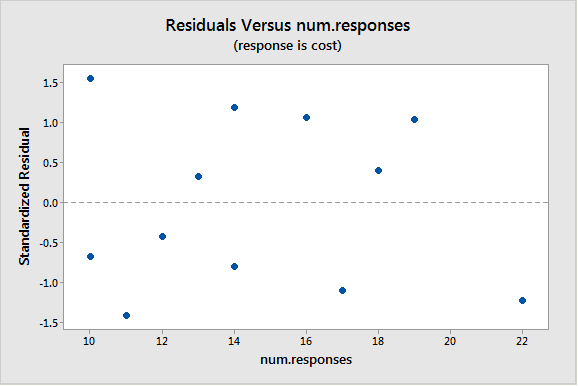
With weighted least squares, it is crucial that we use studentized residuals to evaluate the aptness of the model since these take into account the weights that are used to model the changing variance. The usual residuals don't do this and will maintain the same non-constant variance pattern no matter what weights have been used in the analysis.
Example 13-2: Market Share Data
Here we have market share data for n = 36 consecutive months (Market Share data). Let Y = market share of the product; \(X_1\) = price; \(X_2\) = 1 if the discount promotion is in effect and 0 otherwise; \(X_2\)\(X_3\) = 1 if both discount and package promotions in effect and 0 otherwise. The regression results below are for a useful model in this situation:
Coefficients
| Term | Coef | SE Coef | T-Value | P-Value | VIF |
|---|---|---|---|---|---|
| Constant | 3.196 | 0.356 | 8.97 | 0.000 | |
| Price | -0.334 | 0.152 | -2.19 | 0.036 | 1.01 |
| Discount | 0.3081 | 0.0641 | 4.80 | 0.000 | 1.68 |
| DiscountPromotion | 0.1762 | 0.0660 | 2.67 | 0.012 | 1.69 |
This model represents three different scenarios:
- Months in which there was no discount (and either a package promotion or not): X2 = 0 (and X3 = 0 or 1);
- Months in which there was a discount but no package promotion: X2 = 1 and X3 = 0;
- Months in which there was both a discount and a package promotion: X2 = 1 and X3 = 1.
So, it is fine for this model to break the hierarchy if there is no significant difference between the months in which there was no discount and no package promotion and months in which there was no discount but there was a package promotion.
A residual plot suggests nonconstant variance related to the value of \(X_2\):
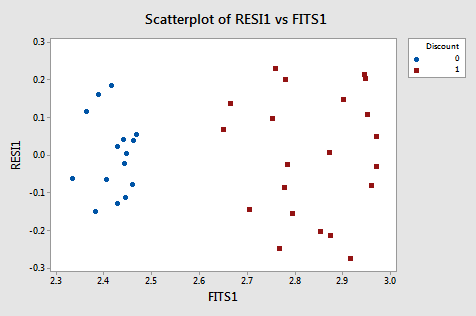
From this plot, it is apparent that the values coded as 0 have a smaller variance than the values coded as 1. The residual variances for the two separate groups defined by the discount pricing variable are:
| Discount | N | StDev | Variance | 95% CI for StDevs |
|---|---|---|---|---|
| 0 | 15 | 0.103 | 0.011 | (0.077, 0.158) |
| 1 | 21 | 0.164 | 0.027 | (0.136, 0.217) |
Because of this nonconstant variance, we will perform a weighted least squares analysis. For the weights, we use \(w_i=1 / \hat{\sigma}_i^2\) for i = 1, 2 (in Minitab use Calc > Calculator and define "weight" as ‘Discount'/0.027 + (1-‘Discount')/0.011 . The weighted least squares analysis (set the just-defined "weight" variable as "weights" under Options in the Regression dialog) is as follows:
Analysis of Variance
| Source | DF | Adj SS | Adj MS | F-Value | P-Value |
|---|---|---|---|---|---|
| Regression | 3 | 96.109 | 32.036 | 30.84 | 0.000 |
| Price | 1 | 4.688 | 4.688 | 4.51 | 0.041 |
| Discount | 1 | 23.039 | 23.039 | 22.18 | 0.000 |
| DiscountPromotion | 1 | 5.634 | 5.634 | 5.42 | 0.026 |
| Error | 32 | 33.246 | 1.039 | ||
| Total | 35 | 129.354 |
Coefficients
| Term | Coef | SE Coef | T-Value | P-Value | VIF |
|---|---|---|---|---|---|
| Constant | 3.175 | 0.357 | 8.90 | 0.000 | |
| Price | -0.325 | 0.153 | -2.12 | 0.041 | 1.01 |
| Discount | 0.3083 | 0.0655 | 4.71 | 0.000 | 2.04 |
| DiscountPromotion | 0.1759 | 0.0755 | 2.33 | 0.026 | 2.05 |
An important note is that Minitab’s ANOVA will be in terms of the weighted SS. When doing a weighted least squares analysis, you should note how different the SS values of the weighted case are from the SS values for the unweighted case.
Also, note how the regression coefficients of the weighted case are not much different from those in the unweighted case. Thus, there may not be much of an obvious benefit to using the weighted analysis (although intervals are going to be more reflective of the data).
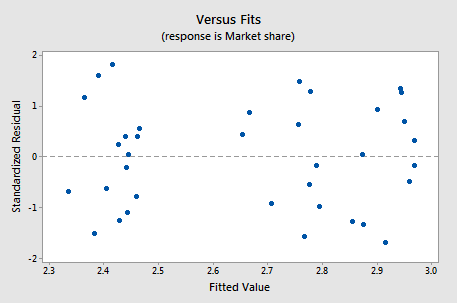
If you proceed with a weighted least squares analysis, you should check a plot of the residuals again. Remember to use the studentized residuals when doing so! For this example, the plot of studentized residuals after doing a weighted least squares analysis is given below and the residuals look okay (remember Minitab calls these standardized residuals).
Example 13-3: Home Price Dataset

The Home Price data set has the following variables:
Y = sale price of a home
\(X_1\) = square footage of the home
\(X_2\) = square footage of the lot
Since all the variables are highly skewed we first transform each variable to its natural logarithm. Then when we perform a regression analysis and look at a plot of the residuals versus the fitted values (see below), we note a slight “megaphone” or “conic” shape of the residuals.
| Term | Coef | SE Coeff | T-Value | P-Value | VIF |
|---|---|---|---|---|---|
| Constant | 1.964 | 0.313 | 6.28 | 0.000 | |
| logX1 | 1.2198 | 0.0340 | 35.87 | 0.000 | 1.05 |
| logX2 | 0.1103 | 0.0241 | 4.57 | 0.000 | 1.05 |
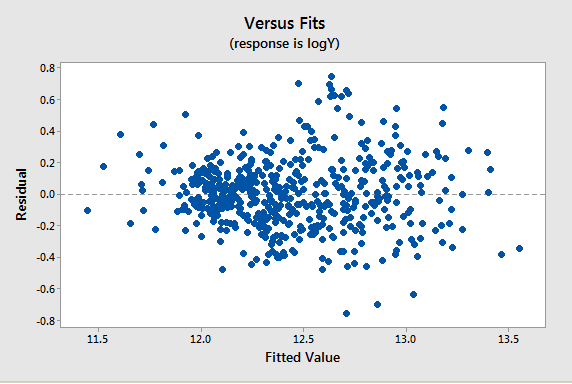
We interpret this plot as having a mild pattern of nonconstant variance in which the amount of variation is related to the size of the mean (which are the fits).
So, we use the following procedure to determine appropriate weights:
- Store the residuals and the fitted values from the ordinary least squares (OLS) regression.
- Calculate the absolute values of the OLS residuals.
- Regress the absolute values of the OLS residuals versus the OLS fitted values and store the fitted values from this regression. These fitted values are estimates of the error standard deviations.
- Calculate weights equal to \(1/fits^{2}\), where "fits" are the fitted values from the regression in the last step.
We then refit the original regression model but use these weights this time in a weighted least squares (WLS) regression.
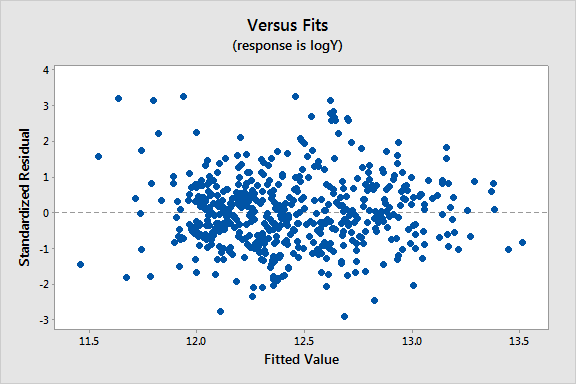
Results and a residual plot for this WLS model:
| Term | Coef | SE Coeff | T-Value | P-Value | VIF |
|---|---|---|---|---|---|
| Constant | 2.377 | 0.284 | 8.38 | 0.000 | |
| logX1 | 1.2014 | 0.0336 | 35.72 | 0.000 | 1.08 |
| logX2 | 0.0831 | 0.0217 | 3.83 | 0.000 | 1.08 |
13.2 - Logistic Regression
13.2 - Logistic RegressionLogistic regression models a relationship between predictor variables and a categorical response variable. For example, we could use logistic regression to model the relationship between various measurements of a manufactured specimen (such as dimensions and chemical composition) to predict if a crack greater than 10 mils will occur (a binary variable: either yes or no). Logistic regression helps us estimate the probability of falling into a certain level of the categorical response given a set of predictors. We can choose from three types of logistic regression, depending on the nature of the categorical response variable:
- Binary Logistic Regression
- Used when the response is binary (i.e., it has two possible outcomes). The cracking example given above would utilize binary logistic regression. Other examples of binary responses could include passing or failing a test, responding yes or no on a survey, and having high or low blood pressure.
- Nominal Logistic Regression
- Used when there are three or more categories with no natural ordering to the levels. Examples of nominal responses could include departments at a business (e.g., marketing, sales, HR), type of search engine used (e.g., Google, Yahoo!, MSN), and color (black, red, blue, orange).
- Ordinal Logistic Regression
- Used when there are three or more categories with a natural ordering to the levels, but the ranking of the levels does not necessarily mean the intervals between them are equal. Examples of ordinal responses could be how students rate the effectiveness of a college course on a scale of 1-5, levels of flavors for hot wings, and medical condition (e.g., good, stable, serious, critical).
Particular issues with modeling a categorical response variable include nonnormal error terms, nonconstant error variance, and constraints on the response function (i.e., the response is bounded between 0 and 1). We will investigate ways of dealing with these in the binary logistic regression setting here. There is some discussion of the nominal and ordinal logistic regression settings in Section 15.2.
The multiple binary logistic regression model is the following:
\(\begin{align}\label{logmod}
\pi&=\dfrac{\exp(\beta_{0}+\beta_{1}X_{1}+\ldots+\beta_{p-1}X_{p-1})}{1+\exp(\beta_{0}+\beta_{1}X_{1}+\ldots+\beta_{p-1}X_{p-1})}\notag \\
&
=\dfrac{\exp(\textbf{X}\beta)}{1+\exp(\textbf{X}\beta)}\\
&
=\dfrac{1}{1+\exp(-\textbf{X}\beta)}
\end{align}\)
where here \(\pi\) denotes a probability and not the irrational number 3.14...
- \(\pi\) is the probability that an observation is in a specified category of the binary Y variable, generally called the "success probability."
- Notice that the model describes the probability of an event happening as a function of X variables. For instance, it might provide estimates of the probability that an older person has heart disease.
- With the logistic model, estimates of \(\pi\) from equations like the one above will always be between 0 and 1. The reasons are:
- The numerator \(\exp(\beta_{0}+\beta_{1}X_{1}+\ldots+\beta_{p-1}X_{p-1})\) must be positive because it is a power of a positive value (e).
- The denominator of the model is (1 + numerator), so the answer will always be less than 1.
- With one X variable, the theoretical model for \(\pi\) has an elongated "S" shape (or sigmoidal shape) with asymptotes at 0 and 1, although in sample estimates we may not see this "S" shape if the range of the X variable is limited.
For a sample of size n, the likelihood for a binary logistic regression is given by:
\(\begin{align*}
L(\beta;\textbf{y},\textbf{X})&=\prod_{i=1}^{n}\pi_{i}^{y_{i}}(1-\pi_{i})^{1-y_{i}}\\
&
=\prod_{i=1}^{n}\biggl(\dfrac{\exp(\textbf{X}_{i}\beta)}{1+\exp(\textbf{X}_{i}\beta)}\biggr)^{y_{i}}\biggl(\dfrac{1}{1+\exp(\textbf{X}_{i}\beta)}\biggr)^{1-y_{i}}.
\end{align*}\)
This yields the log-likelihood:
\(\begin{align*}
\ell(\beta)&=\sum_{i=1}^{n}(y_{i}\log(\pi_{i})+(1-y_{i})\log(1-\pi_{i}))\\
&
=\sum_{i=1}^{n}(y_{i}\textbf{X}_{i}\beta-\log(1+\exp(\textbf{X}_{i}\beta))).
\end{align*}\)
Maximizing the likelihood (or log-likelihood) has no closed-form solution, so a technique like iteratively reweighted least squares is used to find an estimate of the regression coefficients, \(\hat{\beta}\).
To illustrate, consider data published on n = 27 leukemia patients. The Leukemia Remission data set has a response variable of whether leukemia remission occurred (REMISS), which is given by a 1.
The predictor variables are cellularity of the marrow clot section (CELL), smear differential percentage of blasts (SMEAR), percentage of absolute marrow leukemia cell infiltrate (INFIL), percentage labeling index of the bone marrow leukemia cells (LI), the absolute number of blasts in the peripheral blood (BLAST), and the highest temperature before the start of treatment (TEMP).
The following gives the estimated logistic regression equation and associated significance tests from Minitab:
- Select Stat > Regression > Binary Logistic Regression > Fit Binary Logistic Model.
- Select "REMISS" for the Response (the response event for remission is 1 for this data).
- Select all the predictors as Continuous predictors.
- Click Options and choose Deviance or Pearson residuals for diagnostic plots.
- Click Graphs and select "Residuals versus order."
- Click Results and change "Display of results" to "Expanded tables."
- Click Storage and select "Coefficients."
This results in the following output:
Coefficients
| Term | Coef | SE Coef | 95% CI | Z-Value | P-Value | VIF |
|---|---|---|---|---|---|---|
| Constant | 64.3 | 75.0 | ( -82.7, 211.2) | 0.86 | 0.391 | |
| CELL | 30.8 | 52.1 | ( -71.4, 133.0) | 0.59 | 0.554 | 62.46 |
| SMEAR | 24.7 | 61.5 | ( -95.9, 145.3) | 0.40 | 0.688 | 434.42 |
| INFILL | -25.0 | 65.3 | ( - 152.9, 103.0) | -0.38 | 0.702 | 471.10 |
| LI | 4.36 | 2.66 | ( -0.85, 9.57) | 1.64 | 0.101 | 4.43 |
| Blast | -0.01 | 2.27 | ( -4.45, 4.43) | -0.01 | 0.996 | 4.18 |
| TEMP | -100.2 | 77.8 | (-252.6, 52.2) | -1.29 | 0.198 | 3.01 |
Wald Test
The Wald test is the test of significance for individual regression coefficients in logistic regression (recall that we use t-tests in linear regression). For maximum likelihood estimates, the ratio
\(\begin{equation*}
Z=\dfrac{\hat{\beta}_{i}}{\textrm{s.e.}(\hat{\beta}_{i})}
\end{equation*}\)
can be used to test \(H_{0} \colon \beta_{i}=0\). The standard normal curve is used to determine the \(p\)-value of the test. Furthermore, confidence intervals can be constructed as
\(\begin{equation*}
\hat{\beta}_{i}\pm z_{1-\alpha/2}\textrm{s.e.}(\hat{\beta}_{i}).
\end{equation*}\)
Estimates of the regression coefficients, \(\hat{\beta}\), are given in the Minitab output Coefficients table in the column labeled "Coef." This table also gives coefficient p-values based on Wald tests. The index of the bone marrow leukemia cells (LI) has the smallest p-value and so appears to be closest to a significant predictor of remission occurring. After looking at various subsets of the data, we find that a good model is one that only includes the labeling index as a predictor:
Coefficients
| Term | Coef | SE Coef | 95% CI | Z-Value | P-Value | VIF |
|---|---|---|---|---|---|---|
| Constant | -3.78 | 1.38 | ( -6.48, -1.08) | -2.74 | 0.006 | |
| LI | 2.90 | 1.19 | ( -0.57, 5.22) | 2.44 | 0.015 | 1.00 |
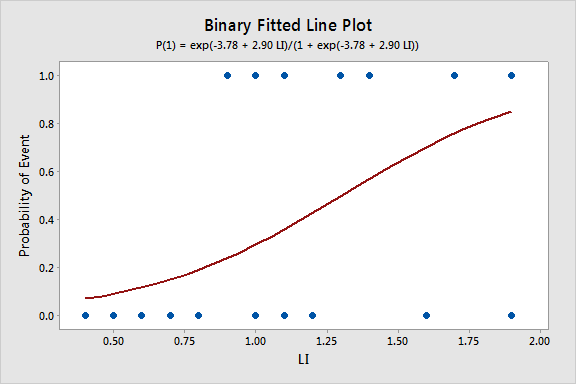
Regression Equation
p(1) = exp(Y')/(1 + exp(Y'))
Y' = -3.78 + 2.90 LI
Since we only have a single predictor in this model we can create a Binary Fitted Line Plot to visualize the sigmoidal shape of the fitted logistic regression curve:
Odds, Log Odds, and Odds Ratio
There are algebraically equivalent ways to write the logistic regression model:
The first is
\(\begin{equation}\label{logmod1}
\dfrac{\pi}{1-\pi}=\exp(\beta_{0}+\beta_{1}X_{1}+\ldots+\beta_{p-1}X_{p-1}),
\end{equation}\)
which is an equation that describes the odds of being in the current category of interest. By definition, the odds for an event is \(\pi\) / (1 - π) such that π is the probability of the event. For example, if you are at the racetrack and there is an 80% chance that a certain horse will win the race, then his odds are 0.80 / (1 - 0.80) = 4, or 4:1.
The second is
\(\begin{equation}\label{logmod2}
\log\biggl(\dfrac{\pi}{1-\pi}\biggr)=\beta_{0}+\beta_{1}X_{1}+\ldots+\beta_{p-1}X_{p-1},
\end{equation}\)
which states that the (natural) logarithm of the odds is a linear function of the X variables (and is often called the log odds). This is also referred to as the logit transformation of the probability of success, \(\pi\).
The odds ratio (which we will write as \(\theta\)) between the odds for two sets of predictors (say \(\textbf{X}_{(1)}\) and \(\textbf{X}_{(2)}\)) is given by
\(\begin{equation*}
\theta=\dfrac{(\pi/(1-\pi))|_{\textbf{X}=\textbf{X}_{(1)}}}{(\pi/(1-\pi))|_{\textbf{X}=\textbf{X}_{(2)}}}.
\end{equation*}\)
For binary logistic regression, the odds of success are:
\(\begin{equation*}
\dfrac{\pi}{1-\pi}=\exp(\textbf{X}\beta).
\end{equation*}\)
By plugging this into the formula for \(\theta\) above and setting \(\textbf{X}_{(1)}\) equal to \(\textbf{X}_{(2)}\) except in one position (i.e., only one predictor differs by one unit), we can determine the relationship between that predictor and the response. The odds ratio can be any nonnegative number. An odds ratio of 1 serves as the baseline for comparison and indicates there is no association between the response and predictor. If the odds ratio is greater than 1, then the odds of success are higher for higher levels of a continuous predictor (or for the indicated level of a factor). In particular, the odds increase multiplicatively by \(\exp(\beta_{j})\) for every one-unit increase in \(\textbf{X}_{j}\). If the odds ratio is less than 1, then the odds of success are less for higher levels of a continuous predictor (or for the indicated level of a factor). Values farther from 1 represent stronger degrees of association.
For example, when there is just a single predictor, \(X\), the odds of success are:
\(\begin{equation*}
\dfrac{\pi}{1-\pi}=\exp(\beta_0+\beta_1X).
\end{equation*}\)
If we increase \(X\) by one unit, the odds ratio is
\(\begin{equation*}
\theta=\dfrac{\exp(\beta_0+\beta_1(X+1))}{\exp(\beta_0+\beta_1X)}=\exp(\beta_1).
\end{equation*}\)
To illustrate, the relevant Minitab output from the leukemia example is:
Odd Ratios for Continuous Predictors
| Odds Ratio | 95% CI | |
|---|---|---|
| LI | 18.1245 | (1.7703, 185.5617) |
The odds ratio for LI of 18.1245 is calculated as \(\exp(2.89726)\) (you can view more decimal places for the coefficient estimates in Minitab by clicking "Storage" in the Regression Dialog and selecting "Coefficients"). The 95% confidence interval is calculated as \(\exp(2.89726\pm z_{0.975}*1.19)\), where \(z_{0.975}=1.960\) is the \(97.5^{\textrm{th}}\) percentile from the standard normal distribution. The interpretation of the odds ratio is that for every increase of 1 unit in LI, the estimated odds of leukemia remission are multiplied by 18.1245. However, since the LI appears to fall between 0 and 2, it may make more sense to say that for every .1 unit increase in L1, the estimated odds of remission are multiplied by \(\exp(2.89726\times 0.1)=1.336\). Then
- At LI=0.9, the estimated odds of leukemia remission is \(\exp\{-3.77714+2.89726*0.9\}=0.310\).
- At LI=0.8, the estimated odds of leukemia remission is \(\exp\{-3.77714+2.89726*0.8\}=0.232\).
- The resulting odds ratio is \(\dfrac{0.310}{0.232}=1.336\), which is the ratio of the odds of remission when LI=0.9 compared to the odds when L1=0.8.
Notice that \(1.336\times 0.232=0.310\), which demonstrates the multiplicative effect by \(\exp(0.1\hat{\beta_{1}})\) on the odds.
Likelihood Ratio (or Deviance) Test
The likelihood ratio test is used to test the null hypothesis that any subset of the \(\beta\)'s is equal to 0. The number of \(\beta\)'s in the full model is p, while the number of \(\beta\)'s in the reduced model is r. (Remember the reduced model is the model that results when the \(\beta\)'s in the null hypothesis are set to 0.) Thus, the number of \(\beta\)'s being tested in the null hypothesis is \(p-r\). Then the likelihood ratio test statistic is given by:
\(\begin{equation*}
\Lambda^{*}=-2(\ell(\hat{\beta}^{(0)})-\ell(\hat{\beta})),
\end{equation*}\)
where \(\ell(\hat{\beta})\) is the log-likelihood of the fitted (full) model and \(\ell(\hat{\beta}^{(0)})\) is the log-likelihood of the (reduced) model specified by the null hypothesis evaluated at the maximum likelihood estimate of that reduced model. This test statistic has a \(\chi^{2}\) distribution with \(p-r\) degrees of freedom. Minitab presents results for this test in terms of "deviance," which is defined as \(-2\) times log-likelihood. The notation used for the test statistic is typically \(G^2\) = deviance (reduced) – deviance (full).
This test procedure is analogous to the general linear F test for multiple linear regression. However, note that when testing a single coefficient, the Wald test and likelihood ratio test will not, in general, give identical results.
To illustrate, the relevant software output from the leukemia example is:
Deviance Table
| Source | DF | Adj Dev | Adj Mean | Chi-Square | P-Value |
|---|---|---|---|---|---|
| Regression | 1 | 8.299 | 8.299 | 8.30 | 0.004 |
| LI | 1 | 8.299 | 8.299 | 8.30 | 0.004 |
| Error | 25 | 26.073 | 1.043 | ||
| Total | 26 | 34.372 |
Since there is only a single predictor for this example, this table simply provides information on the likelihood ratio test for LI (p-value of 0.004), which is similar but not identical to the earlier Wald test result (p-value of 0.015). The Deviance Table includes the following:
- The null (reduced) model, in this case, has no predictors, so the fitted probabilities are simply the sample proportion of successes, \(9/27=0.333333\). The log-likelihood for the null model is \(\ell(\hat{\beta}^{(0)})=-17.1859\), so the deviance for the null model is \(-2\times-17.1859=34.372\), which is shown in the "Total" row in the Deviance Table.
- The log-likelihood for the fitted (full) model is \(\ell(\hat{\beta})=-13.0365\), so the deviance for the fitted model is \(-2\times-13.0365=26.073\), which is shown in the "Error" row in the Deviance Table.
- The likelihood ratio test statistic is therefore \(\Lambda^{*}=-2(-17.1859-(-13.0365))=8.299\), which is the same as \(G^2=34.372-26.073=8.299\).
- The p-value comes from a \(\chi^{2}\) distribution with \(2-1=1\) degrees of freedom.
When using the likelihood ratio (or deviance) test for more than one regression coefficient, we can first fit the "full" model to find deviance (full), which is shown in the "Error" row in the resulting full model Deviance Table. Then fit the "reduced" model (corresponding to the model that results if the null hypothesis is true) to find deviance (reduced), which is shown in the "Error" row in the resulting reduced model Deviance Table. For example, the relevant Deviance Tables for the Disease Outbreak example on pages 581-582 of Applied Linear Regression Models (4th ed) by Kutner et al are:
Full model
| Source | DF | Adj Dev | Adj Mean | Chi-Square | P-Value |
|---|---|---|---|---|---|
| Regression | 9 | 28.322 | 3.14686 | 28.32 | 0.001 |
| Error | 88 | 93.996 | 1.06813 | ||
| Total | 97 | 122.318 |
Reduced Model
| Source | DF | Adj Dev | Adj Mean | Chi-Square | P-Value |
|---|---|---|---|---|---|
| Regression | 4 | 21.263 | 5.3159 | 21.26 | 0.000 |
| Error | 93 | 101.054 | 1.06813 | ||
| Total | 97 | 122.318 |
Here the full model includes four single-factor predictor terms and five two-factor interaction terms, while the reduced model excludes the interaction terms. The test statistic for testing the interaction terms is \(G^2 = 101.054-93.996 = 7.058\), which is compared to a chi-square distribution with \(10-5=5\) degrees of freedom to find the p-value > 0.05 (meaning the interaction terms are not significant).
Alternatively, select the corresponding predictor terms last in the full model and request Minitab to output Sequential (Type I) Deviances. Then add the corresponding Sequential Deviances in the resulting Deviance Table to calculate \(G^2\). For example, the relevant Deviance Table for the Disease Outbreak example is:
| Source | DF | Seq Dev | Seq Mean | Chi-Square | P-Value |
|---|---|---|---|---|---|
| Regression | 9 | 28.322 | 3.1469 | 28.32 | 0.001 |
| --Age | 1 | 7.405 | 7.4050 | 7.40 | 0.007 |
| --Middle | 1 | 1.804 | 1.8040 | 1.80 | 0.179 |
| --Lower | 1 | 1.606 | 1.6064 | 1.61 | 0.205 |
| Sector | 1 | 10.448 | 10.4481 | 10.45 | 0.001 |
| Age*Middle | 1 | 4.570 | 4.5397 | 4.57 | 0.033 |
| Age*Lower | 1 | 1.015 | 1.0152 | 1.02 | 0.314 |
| Age*Sector | 1 | 1.120 | 1.1202 | 1.12 | 0.290 |
| Middle*Sector | 1 | 0.000 | 0.0001 | 0.00 | 0.993 |
| Lower*Sector | 1 | 0.353 | 0.3531 | 0.35 | 0.3552 |
| Error | 88 | 93.996 | 1.0681 | ||
| Total | 97 | 122.318 |
The test statistic for testing the interaction terms is \(G^2 = 4.570+1.015+1.120+0.000+0.353 = 7.058\), the same as in the first calculation.
Goodness-of-Fit Tests
The overall performance of the fitted model can be measured by several different goodness-of-fit tests. Two tests that require replicated data (multiple observations with the same values for all the predictors) are the Pearson chi-square goodness-of-fit test and the deviance goodness-of-fit test(analogous to the multiple linear regression lack-of-fit F-test). Both of these tests have statistics that are approximately chi-square distributed with c - p degrees of freedom, where c is the number of distinct combinations of the predictor variables. When a test is rejected, there is a statistically significant lack of fit. Otherwise, there is no evidence of a lack of fit.
By contrast, the Hosmer-Lemeshow goodness-of-fit test is helpful for unreplicated datasets or for datasets that contain just a few replicated observations. For this test, the observations are grouped based on their estimated probabilities. The resulting test statistic is approximately chi-square distributed with c - 2 degrees of freedom, where c is the number of groups (generally chosen to be between 5 and 10, depending on the sample size).
To illustrate, the relevant Minitab output from the leukemia example is:
Goodness-of-Fit Test
| Test | DF | Chi-square | P-Value |
|---|---|---|---|
| Deviance | 25 | 26.07 | 0.404 |
| Pearson | 25 | 23.93 | 0.523 |
| Hosmer-Lemeshow | 7 | 6.87 | 0.442 |
Since there is no replicated data for this example, the deviance and Pearson goodness-of-fit tests are invalid, so the first two rows of this table should be ignored. However, the Hosmer-Lemeshow test does not require replicated data so we can interpret its high p-value as indicating no evidence of lack of fit.
\(R^{2}\)
The calculation of \(R^{2}\) used in linear regression does not extend directly to logistic regression. One version of \(R^{2}\) used in logistic regression is defined as
\(\begin{equation*}
R^{2}=\dfrac{\ell(\hat{\beta_{0}})-\ell(\hat{\beta})}{\ell(\hat{\beta_{0}})-\ell_{S}(\beta)},
\end{equation*}\)
where \(\ell(\hat{\beta_{0}})\) is the log-likelihood of the model when only the intercept is included and \(\ell_{S}(\beta)\) is the log-likelihood of the saturated model (i.e., where a model is fit perfectly to the data). This \(R^{2}\) does go from 0 to 1 with 1 being a perfect fit. With unreplicated data, \(\ell_{S}(\beta)=0\), so the formula simplifies to:
\(\begin{equation*}
R^{2}=\dfrac{\ell(\hat{\beta_{0}})-\ell(\hat{\beta})}{\ell(\hat{\beta_{0}})}=1-\dfrac{\ell(\hat{\beta})}{\ell(\hat{\beta_{0}})}.
\end{equation*}\)
To illustrate, the relevant Minitab output from the leukemia example is:
Model Summary
| Deviance R-Sq |
Deviance R-Sq(adj) |
AIC |
|---|---|---|
| 24.14% | 21.23% | 30.07 |
Recall from above that \(\ell(\hat{\beta})=-13.0365\) and \(\ell(\hat{\beta}^{(0)})=-17.1859\), so:
\(\begin{equation*}
R^{2}=1-\dfrac{-13.0365}{-17.1859}=0.2414.
\end{equation*}\)
Note that we can obtain the same result by simply using deviances instead of log-likelihoods since the \(-2\) factor cancels out:
\(\begin{equation*}
R^{2}=1-\dfrac{26.073}{34.372}=0.2414.
\end{equation*}\)
Raw Residual
The raw residual is the difference between the actual response and the estimated probability from the model. The formula for the raw residual is
\(\begin{equation*}
r_{i}=y_{i}-\hat{\pi}_{i}.
\end{equation*}\)
Pearson Residual
The Pearson residual corrects for the unequal variance in the raw residuals by dividing by the standard deviation. The formula for the Pearson residuals is
\(\begin{equation*}
p_{i}=\dfrac{r_{i}}{\sqrt{\hat{\pi}_{i}(1-\hat{\pi}_{i})}}.
\end{equation*}\)
Deviance Residuals
Deviance residuals are also popular because the sum of squares of these residuals is the deviance statistic. The formula for the deviance residual is
\(\begin{equation*}
d_{i}=\pm\sqrt{2\biggl(y_{i}\log\biggl(\dfrac{y_{i}}{\hat{\pi}_{i}}\biggr)+(1-y_{i})\log\biggl(\dfrac{1-y_{i}}{1-\hat{\pi}_{i}}\biggr)\biggr)}.
\end{equation*}\)
Here are the plots of the Pearson residuals and deviance residuals for the leukemia example. There are no alarming patterns in these plots to suggest a major problem with the model.
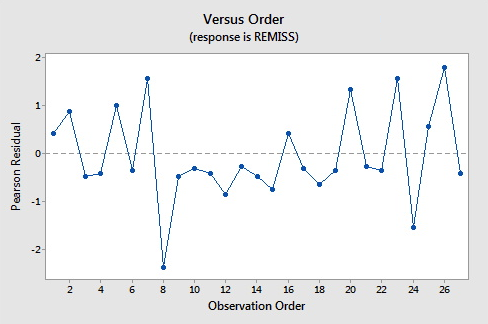
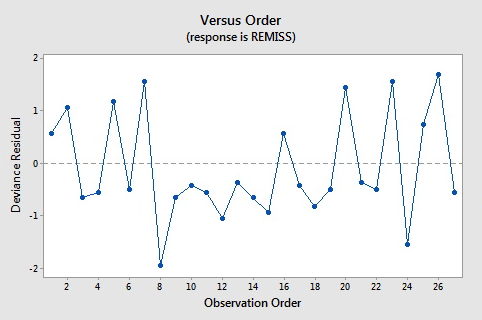
Hat Values
The hat matrix serves a similar purpose as in the case of linear regression – to measure the influence of each observation on the overall fit of the model – but the interpretation is not as clear due to its more complicated form. The hat values (leverages) are given by
\(\begin{equation*}
h_{i,i}=\hat{\pi}_{i}(1-\hat{\pi}_{i})\textbf{x}_{i}^{\textrm{T}}(\textbf{X}^{\textrm{T}}\textbf{W}\textbf{X})\textbf{x}_{i},
\end{equation*}\)
where W is an \(n\times n\) diagonal matrix with the values of \(\hat{\pi}_{i}(1-\hat{\pi}_{i})\) for \(i=1 ,\ldots,n\) on the diagonal. As before, we should investigate any observations with \(h_{i,i}>3p/n\) or, failing this, any observations with \(h_{i,i}>2p/n\) and very isolated.
Studentized Residuals
We can also report Studentized versions of some of the earlier residuals. The Studentized Pearson residuals are given by
\(\begin{equation*}
sp_{i}=\dfrac{p_{i}}{\sqrt{1-h_{i,i}}}
\end{equation*}\)
and the Studentized deviance residuals are given by
\(\begin{equation*}
sd_{i}=\dfrac{d_{i}}{\sqrt{1-h_{i, i}}}.
\end{equation*}\)
C and \(\bar{\textrm{C}}\)
C and \(\bar{\textrm{C}}\) are extensions of Cook's distance for logistic regression. C measures the overall change in fitted logits due to deleting the \(i^{\textrm{th}}\) observation for all points including the one deleted, while \(\bar{\textrm{C}}\) excludes the deleted point. They are defined by:
\(\begin{equation*}
\textrm{C}_{i}=\dfrac{p_{i}^{2}h _{i,i}}{p(1-h_{i,i})^{2}}
\end{equation*}\)
and
\(\begin{equation*}
\bar{\textrm{C}}_{i}=\dfrac{p_{i}^{2}h_{i,i}}{p(1-h_{i,i})}.
\end{equation*}\)
To illustrate, the relevant Minitab output from the leukemia example is:
Fits and Diagnostics for Unusual Observations
| Obs | Probability | Fit | SE Fit | 95% CI | Resid | Std Resid | Del Resid | HI |
|---|---|---|---|---|---|---|---|---|
| 8 | 0.000 | 0.849 | 0.139 | (0.403, 0.979) | -1.945 | -2.11 | -2.19 | 0.149840 |
Fits and Diagnostics for Unusual Observations
| Obs | Cook's D | DFITS | |
|---|---|---|---|
| 8 | 0.58 | -1.08011 | R |
R Large residual
The default residuals in this output (set under Minitab's Regression Options) are deviance residuals, so observation 8 has a deviance residual of \(-1.945\), a studentized deviance residual of \(-2.11\), a leverage (h) of \(0.149840\), and a Cook's distance (C) of 0.58.
DFDEV and DFCHI
DFDEV and DFCHI are statistics that measure the change in deviance and in Pearson's chi-square, respectively, that occurs when an observation is deleted from the data set. Large values of these statistics indicate observations that have not been fitted well. The formulas for these statistics are
\(\begin{equation*}
\textrm{DFDEV}_{i}=d_{i}^{2}+\bar{\textrm{C}}_{i}
\end{equation*}\)
and
\(\begin{equation*}
\textrm{DFCHI}_{i}=\dfrac{\bar{\textrm{C}}_{i}}{h_{i,i}}
\end{equation*}\)
13.2.1 - Further Logistic Regression Examples
13.2.1 - Further Logistic Regression ExamplesExample 15-1: STAT 200 Dataset
Students in STAT 200 at Penn State were asked if they have ever driven after drinking (the dataset unfortunately no longer available). They also were asked, “How many days per month do you drink at least two beers?” In the following discussion, \(\pi\) = the probability a student says “yes” they have driven after drinking. This is modeled using X = days per month of drinking two beers. Results from Minitab were as follows.
| Variable | Value | Count |
|---|---|---|
| DrivDrnk | Yes | 122 (Event) |
| No | 127 | |
| Total | 249 |
| 95% CI | |||||||
|---|---|---|---|---|---|---|---|
| Coef | SE Coef | Z | P | Odds Ratio | Lower | Upper | |
| Constant | -1.5514 | 0.2661 | -5.83 | 0.000 | |||
| DaysBeer | 0.19031 | 0.02946 | 6.46 | 0.000 | 1.21 | 1.14 | 1.28 |
Some things to note from the results are:
- We see that in the sample 122/249 students said they have driven after drinking. (Yikes!)
- Parameter estimates, given under Coef are \(\hat{\beta}_0\) = −1.5514, and \(\hat{\beta}_1\) = 0.19031.
- The model for estimating \(\pi\) = the probability of ever having driven after drinking is
\(\hat{\pi}=\dfrac{\exp(-1.5514+0.19031X)}{1+\exp(-1.5514+0.19031X)}\)
- The variable X = DaysBeer is a statistically significant predictor (Z = 6.46, P = 0.000).
We can also obtain a plot of the estimated probability of ever having driven under the influence (\(\pi\)) versus days per month of drinking at least two beers.
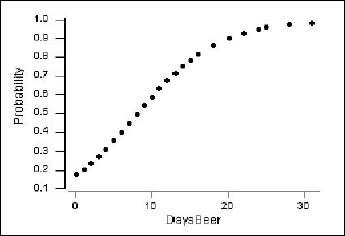
The vertical axis shows the probability of ever having driven after drinking. For example, if X = 4 days per month of drinking beer, then the estimated probability is calculated as:
\(\hat{\pi}=\dfrac{\exp(-1.5514+0.19031(4))}{1+\exp(-1.5514+0.19031(4))}=\frac{\exp(-0.79016)}{1+\exp(-0.79016)}=0.312\)
A few of these estimated probabilities are given in the following table:
| DaysBeer | 4 | 12 | 20 | 28 |
|---|---|---|---|---|
| \(\hat{\pi}\) | 0.312 | 0.675 | 0.905 | 0.97 |
In the results given above, we see that the estimate of the odds ratio is 1.21 for DaysBeer. This is given under Odds Ratio in the table of coefficients, standard errors, and so on. The sample odds ratio was calculated as \(e^{0.19031}\). The interpretation of the odds ratio is that for each increase of one day of drinking beer per month, the predicted odds of having ever driven after drinking are multiplied by 1.21.
Above we found that at X = 4, the predicted probability of ever driving after drinking is \(\hat{\pi}\) = 0.312. Thus when X = 4, the predicted odds of ever driving after drinking is 0.312/(1 − 0.312) = 0.453. To find the odds when X = 5, one method would be to multiply the odds at X = 4 by the sample odds ratio. The calculation is 1.21 × 0.453 = 0.549. (Another method is to just do the calculation as we did for X = 4.)
Notice also, that the results give a 95% confidence interval estimate of the odd ratio (1.14 to 1.28).
We now include Gender (male or female) as an x-variable (along with DaysBeer). Some Minitab results are given below. Under Gender, the row for male is explaining that the program created an indicator variable with a value of 1 if the student is male and a value of 0 if the student is female.
| 95% CI | |||||||
|---|---|---|---|---|---|---|---|
| Coef | SE Coef | Z | P | Odds Ratio | Lower | Upper | |
| Constant | -1.7736 | 0.2945 | -6.02 | 0.000 | |||
| DaysBeer | 0.18693 | 0.03004 | 6.22 | 0.000 | 1.21 | 1.14 | 1.28 |
|
Gender male |
0.6172 | 0.2954 | 2.09 | 0.037 | 1.85 | 1.04 | 3.31 |
Some things to note from the results are:
- The p-values are less than 0.05 for both DaysBeer and Gender. This is evidence that both x-variables are useful for predicting the probability of ever having driven after drinking.
- For DaysBeer, the odds ratio is still estimated to equal 1.21 to two decimal places (calculated as \(e^{0.18693}\)).
- For Gender, the odds ratio is 1.85 (calculated as \(e^{0.6172}\)). For males, the odds of ever having driven after drinking is 1.85 times the odds for females, assuming DaysBeer is held constant.
Finally, the results for testing with respect to the multiple logistic regression model are as follows:
Log-Likelihood = -139.981
Test that all slopes are zero: G = 65.125, DF = 2, P-Value = 0.000
Notice that since we have a p-value of 0.000 for this chi-square test, we, therefore, reject the null hypothesis that all of the slopes are equal to 0.
Example 15-2: Toxicity Dataset

An experiment is done to test the effect of a toxic substance on insects. The data originate from the textbook, Applied Linear Statistical Models by Kutner, Nachtsheim, Neter, & Li.
At each of six dose levels, 250 insects are exposed to the substance and the number of insects that die is counted (Toxicity data). We can use Minitab to calculate the observed probabilities as the number of observed deaths out of 250 for each dose level.
A binary logistic regression model is used to describe the connection between the observed probabilities of death as a function of dose level. Since the data is in event/trial format the procedure in Minitab is a little different to before:
- Select Stat > Regression > Binary Logistic Regression > Fit Binary Logistic Model
- Select "Response is in event/trial format"
- Select "Deaths" for Number of events, "SampSize" for Number of trials (and type "Death" for Event name if you like)
- Select Dose as a Continuous predictor
- Click Results and change "Display of results" to "Expanded tables"
- Click Storage and select "Fits (event probabilities)"
The Minitab output is as follows:
Coefficients
| Term | Coef | SE Coef | 95% CI | Z | P | VIF |
|---|---|---|---|---|---|---|
| Constant | -2.644 | 0.156 | (-2.950, -2.338) | -16.94 | 0.000 | |
| Dose | 0.6740 | 0.0391 | (0.5973, 0.7506) | 17.23 | 0.000 | 1.00 |
Odds Ratios for Continuous Predictors
| Term | Odds Ratio | 95% CI |
|---|---|---|
| Dose | 1.9621 | (1.8173, 2.1184) |
Thus
\(\hat{\pi}=\dfrac{\exp(-2.644+0.674X)}{1+\exp(-2.644+0.674X)}\)
where X = Dose and \(\hat{\pi}\) is the estimated probability the insect dies (based on the model).
Predicted probabilities of death (based on the logistic model) for the six dose levels are given below (FITS). These probabilities closely agree with the observed values (Observed p) reported.
Data Display
| Row | Dose | SampSize | Deaths | Observed P | FITS |
|---|---|---|---|---|---|
| 1 | 1 | 250 | 28 | 0.112 | 0.122423 |
| 2 | 2 | 250 | 53 | 0.212 | 0.214891 |
| 3 | 3 | 250 | 93 | 0.372 | 0.349396 |
| 4 | 4 | 250 | 126 | 0.504 | 0.513071 |
| 5 | 5 | 250 | 172 | 0.688 | 0.673990 |
| 6 | 6 | 250 | 197 | 0.788 | 0.802229 |
As an example of calculating the estimated probabilities, for Dose 1, we have
\(\hat{\pi}=\dfrac{\exp(-2.644+0.674(1))}{1+\exp(-2.644+0.674(1))}=0.1224\)
The odds ratio for Dose is 1.9621, the value under Odds Ratio in the output. It was calculated as \(e^{0.674}\). The interpretation of the odds ratio is that for every increase of 1 unit in dose level, the estimated odds of insect death are multiplied by 1.9621.
As an example of odds and odds ratio:
- At Dose = 1, the estimated odds of death is \(\hat{\pi}/(1− \hat{\pi})\) = 0.1224/(1−0.1224) = 0.1395.
- At Dose = 2, the estimated odds of death is \(\hat{\pi}/(1− \hat{\pi})\) = 0.2149/(1−0.2149) = 0.2737.
- The Odds Ratio = \(\dfrac{0.2737}{0.1395}\), which is the ratio of the odds of death when Dose = 2 compared to the odds when Dose = 1.
A property of the binary logistic regression model is that the odds ratio is the same for any increase of one unit in X, regardless of the specific values of X.
Software Help 13
Software Help 13
The next two pages cover the Minitab and R commands for the procedures in this lesson.
Below is a zip file that contains all the data sets used in this lesson:
- ca_learning.txt
- DiseaseOutbreak
- home_price.txt
- leukemia_remission.txt
- market_share.txt
- quality_measure.txt
- toxicity.txt
Minitab Help 13: Weighted Least Squares & Logistic Regressions
Minitab Help 13: Weighted Least Squares & Logistic RegressionsMinitab®
Galton peas (nonconstant variance and weighted least squares)
- Perform a linear regression analysis to fit an ordinary least squares (OLS) simple linear regression model of Progeny vs Parent (click "Storage" in the regression dialog to store fitted values).
- Select Calc > Calculator to calculate the weights variable = \(1/SD^{2}\) and Perform a linear regression analysis to fit a weighted least squares (WLS) model (click "Options" in the regression dialog to set the weights variable and click "Storage" to store fitted values).
- Create a basic scatterplot< of the data and click Editor > Add > Calculated Line to add a regression line for each model using the stored fitted values.
Computer-assisted learning (nonconstant variance and weighted least squares)
- Create a basic scatterplot of the data.
- Perform a linear regression analysis to fit an OLS model (click "Storage" to store the residuals and the fitted values).
- Create a basic scatterplot of the OLS residuals vs num.responses.
- Select Calc > Calculator to calculate the absolute residuals and Create a basic scatterplot of the absolute OLS residuals vs num.responses.
- Perform a linear regression analysis of absolute residuals vs num.responses (click "Storage" to store the fitted values).
- Select Calc > Calculator to calculate the weights variable = \(1/(\text{fitted values})^{2}\), Perform a linear regression analysis to fit a WLS model (click "Options" to set the weights variable and click "Storage" to store standardized residuals and fitted values).
- Create a basic scatterplot< of the data and click Editor > Add > Calculated Line to add a regression line for each model using the stored fitted values.
- Create a basic scatterplot of the WLS standardized residuals vs num.responses.
Market share (nonconstant variance and weighted least squares)
- Perform a linear regression analysis to fit an OLS model (click "Storage" to store the residuals and fitted values).
- Create a basic scatterplot of the OLS residuals vs fitted values but select "With Groups" to mark the points by Discount.
- Select Stat > Basic Statistics > Display Descriptive Statistics to calculate the residual variance for Discount=0 and Discount=1.
- Select Calc > Calculator to calculate the weights variable = 1/variance for Discount=0 and Discount=1, Perform a linear regression analysis to fit a WLS model (click "Options" to set the weights variable and click "Storage" to store standardized residuals and fitted values).
- Create a basic scatterplot of the WLS standardized residuals vs fitted values.
Home price (nonconstant variance and weighted least squares)
- Select Calc > Calculator to calculate log transformations of the variables.
- Perform a linear regression analysis to fit an OLS model (click "Storage" to store the residuals and fitted values).
- Create a basic scatterplot of the OLS residuals vs fitted values.
- Perform a linear regression analysis of absolute residuals vs fitted values (click "Storage" to store the fitted values).
- Select Calc > Calculator to calculate the weights variable = \(1/(\text{fitted values})^{2}\), Perform a linear regression analysis to fit a WLS model (click "Options" to set the weights variable and click "Storage" to store standardized residuals and fitted values).
- Create a basic scatterplot of the WLS standardized residuals vs fitted values.
Leukemia remission (logistic regression)
- Select Stat > Regression > Binary Logistic Regression > Fit Binary Logistic Model, make sure "Response in binary response/frequency format" is selected, put REMISS in the "Response" box, and put CELL, SMEAR, INFIL, LI, BLAST, and TEMP in the "Continuous predictors" box. Before clicking "OK," click "Results" and select "Expanded tables" for "Display of results."
- Repeat but with just LI as a single predictor.
- Fit a logistic regression model of REMISS vs LI.
- Select Stat > Regression > Binary Fitted Line Plot to create a scatterplot of REMISS vs LI with a fitted line based on the logistic regression model.
- Before clicking "OK" in the Regression Dialog, click "Options" and type "10" into the box labeled "Number of groups for Hosmer-Lemeshow test." This will result in a new table in the output titled "Goodness-of-Fit Tests" with results for Deviance (not valid for this example), Pearson (also not valid for this example), and Hosmer-Lemeshow goodness-of-fit tests.
- Before clicking "OK" in the Regression Dialog, click "Graphs" and select "Residuals versus Order" to create residual plots using deviance residuals. To change to Pearson residuals, click "Options" in the Regression Dialog and select "Pearson" for "Residuals for diagnostics."
Disease outbreak (logistic regression)
- Select Stat > Regression > Binary Logistic Regression > Fit Binary Logistic Model, make sure "Response in binary response/frequency format" is selected, put Disease in the "Response" box, and put Age, Middle, Lower, and Sector in the "Continuous predictors" box. Before clicking "OK," click "Model," shift-select the four predictors in the top-left box, click "Add" next to "Interactions through order 2," but remove the "Middle*Lower" interaction from the "Terms in the model" box since it is meaningless.
- Repeat but with the five interactions removed.
- Repeat but with the five interactions included and before clicking "OK," click "Options" and select "Sequential (Type I)" for "Deviances for tests."
Toxicity and insects (logistic regression using event/trial data format)
- Select Stat > Regression > Binary Logistic Regression > Fit Binary Logistic Model, select "Response in event/trial format," put Deaths in the "Number of events" box, put SampSize in the "Number of trials" box, and put "Dose" in the "Continuous predictors" box. Change "Event name" to "Death" if you like (optional). Before clicking "OK," click "Results" and select "Expanded tables" for "Display of results."
- Select Calc > Calculator to calculate observed probabilities as Deaths/SampSize.
- Before clicking "OK" in the Regression Dialog, click "Storage" and select "Fits (event probabilities)."
- Select Stat > Regression > Binary Fitted Line Plot to create a scatterplot of observed probabilities vs Dose with a fitted line based on the logistic regression model.
R Help 13: Weighted Least Squares & Logistic Regressions
R Help 13: Weighted Least Squares & Logistic RegressionsR Help
Galton peas (nonconstant variance and weighted least squares)
- Load the galton data.
- Fit an ordinary least squares (OLS) simple linear regression model of Progeny vs Parent.
- Fit a weighted least squares (WLS) model using weights = \(1/{SD^2}\).
- Create a scatterplot of the data with a regression line for each model.
galton <- read.table("~/path-to-data/galton.txt", header=T)
attach(galton)
model.1 <- lm(Progeny ~ Parent)
summary(model.1)
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 0.127029 0.006993 18.164 9.29e-06 ***
# Parent 0.210000 0.038614 5.438 0.00285 **
model.2 <- lm(Progeny ~ Parent, weights=1/SD^2)
summary(model.2)
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 0.127964 0.006811 18.787 7.87e-06 ***
# Parent 0.204801 0.038155 5.368 0.00302 **
plot(x=Parent, y=Progeny, ylim=c(0.158,0.174),
panel.last = c(lines(sort(Parent), fitted(model.1)[order(Parent)], col="blue"),
lines(sort(Parent), fitted(model.2)[order(Parent)], col="red")))
legend("topleft", col=c("blue","red"), lty=1,
inset=0.02, legend=c("OLS", "WLS"))
detach(galton)
Computer-assisted learning (nonconstant variance and weighted least squares)
- Load the ca_learning data.
- Create a scatterplot of the data.
- Fit an OLS model.
- Plot the OLS residuals vs num.responses.
- Plot the absolute OLS residuals vs num.responses.
- Calculate fitted values from a regression of absolute residuals vs num.responses.
- Fit a WLS model using weights = \(1/{(\text{fitted values})^2}\).
- Create a scatterplot of the data with a regression line for each model.
- Plot the WLS standardized residuals vs num.responses.
ca_learning <- read.table("~/path-to-data/ca_learning_new.txt", header=T)
attach(ca_learning)
plot(x=num.responses, y=cost)
model.1 <- lm(cost ~ num.responses)
summary(model.1)
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 19.4727 5.5162 3.530 0.00545 **
# num.responses 3.2689 0.3651 8.955 4.33e-06 ***
# ---
# Residual standard error: 4.598 on 10 degrees of freedom
# Multiple R-squared: 0.8891, Adjusted R-squared: 0.878
# F-statistic: 80.19 on 1 and 10 DF, p-value: 4.33e-06
plot(num.responses, residuals(model.1))
plot(num.responses, abs(residuals(model.1)))
wts <- 1/fitted(lm(abs(residuals(model.1)) ~ num.responses))^2
model.2 <- lm(cost ~ num.responses, weights=wts)
summary(model.2)
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 17.3006 4.8277 3.584 0.00498 **
# num.responses 3.4211 0.3703 9.238 3.27e-06 ***
# ---
# Residual standard error: 1.159 on 10 degrees of freedom
# Multiple R-squared: 0.8951, Adjusted R-squared: 0.8846
# F-statistic: 85.35 on 1 and 10 DF, p-value: 3.269e-06
plot(x=num.responses, y=cost, ylim=c(50,95),
panel.last = c(lines(sort(num.responses), fitted(model.1)[order(num.responses)], col="blue"),
lines(sort(num.responses), fitted(model.2)[order(num.responses)], col="red")))
legend("topleft", col=c("blue","red"), lty=1,
inset=0.02, legend=c("OLS", "WLS"))
plot(num.responses, rstandard(model.2))
detach(ca_learning)
Market share (nonconstant variance and weighted least squares)
- Load the marketshare data.
- Fit an OLS model.
- Plot the OLS residuals vs fitted values with points marked by Discount.
- Use the
tapplyfunction to calculate the residual variance for Discount=0 and Discount=1. - Fit a WLS model using weights = 1/variance for Discount=0 and Discount=1.
- Plot the WLS standardized residuals vs fitted values.
marketshare <- read.table("~/path-to-data/marketshare.txt", header=T)
attach(marketshare)
model.1 <- lm(MarketShare ~ Price + P1 + P2)
summary(model.1)
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 3.19592 0.35616 8.973 3.00e-10 ***
# Price -0.33358 0.15226 -2.191 0.0359 *
# P1 0.30808 0.06412 4.804 3.51e-05 ***
# P2 0.48431 0.05541 8.740 5.49e-10 ***
plot(fitted(model.1), residuals(model.1), col=Discount+1)
vars <- tapply(residuals(model.1), Discount, var)
# 0 1
# 0.01052324 0.02680546
wts <- Discount/vars[2] + (1-Discount)/vars[1]
model.2 <- lm(MarketShare ~ Price + P1 + P2, weights=wts)
summary(model.2)
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 3.17437 0.35671 8.899 3.63e-10 ***
# Price -0.32432 0.15291 -2.121 0.0418 *
# P1 0.30834 0.06575 4.689 4.89e-05 ***
# P2 0.48419 0.05422 8.930 3.35e-10 ***
plot(fitted(model.2), rstandard(model.2), col=Discount+1)
detach(marketshare)
Home price (nonconstant variance and weighted least squares)
- Load the realestate data.
- Calculate log transformations of the variables.
- Fit an OLS model.
- Plot the OLS residuals vs fitted values.
- Calculate fitted values from a regression of absolute residuals vs fitted values.
- Fit a WLS model using weights = \(1/{(\text{fitted values})^2}\).
- Plot the WLS standardized residuals vs fitted values.
realestate <- read.table("~/path-to-data/realestate.txt", header=T)
attach(realestate)
logY <- log(SalePrice)
logX1 <- log(SqFeet)
logX2 <- log(Lot)
model.1 <- lm(logY ~ logX1 + logX2)
summary(model.1)
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 4.25485 0.07353 57.864 < 2e-16 ***
# logX1 1.22141 0.03371 36.234 < 2e-16 ***
# logX2 0.10595 0.02394 4.425 1.18e-05 ***
plot(fitted(model.1), residuals(model.1))
wts <- 1/fitted(lm(abs(residuals(model.1)) ~ fitted(model.1)))^2
model.2 <- lm(logY ~ logX1 + logX2, weights=wts)
summary(model.2)
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 4.35189 0.06330 68.755 < 2e-16 ***
# logX1 1.20150 0.03332 36.065 < 2e-16 ***
# logX2 0.07924 0.02152 3.682 0.000255 ***
plot(fitted(model.2), rstandard(model.2))
detach(realestate)
Leukemia remission (logistic regression)
- Load the leukemia data.
- Fit a logistic regression model of REMISS vs CELL + SMEAR + INFIL + LI + BLAST + TEMP.
- Calculate 95% confidence intervals for the regression parameters based on asymptotic normality and based on profiling the least-squares estimation surface.
- Fit a logistic regression model of REMISS vs LI.
- Create a scatterplot of REMISS vs LI and add a fitted line based on the logistic regression model.
- Calculate the odds ratio for LI and a 95% confidence interval.
- Conduct a likelihood ratio (or deviance) test for LI.
- Calculate the sum of squared deviance residuals and the sum of squared Pearson residuals.
- Use the
hoslem.testfunction in theResourceSelectionpackage to conduct the Hosmer-Lemeshow goodness-of-fit test. - Calculate a version of \(R^2\) for logistic regression.
- Create residual plots using Pearson and deviance residuals.
- Calculate hat values (leverages), studentized residuals, and Cook's distances.
leukemia <- read.table("~/path-to-data/leukemia_remission.txt", header=T)
attach(leukemia)
model.1 <- glm(REMISS ~ CELL + SMEAR + INFIL + LI + BLAST + TEMP, family="binomial")
summary(model.1)
# Estimate Std. Error z value Pr(>|z|)
# (Intercept) 64.25808 74.96480 0.857 0.391
# CELL 30.83006 52.13520 0.591 0.554
# SMEAR 24.68632 61.52601 0.401 0.688
# INFIL -24.97447 65.28088 -0.383 0.702
# LI 4.36045 2.65798 1.641 0.101
# BLAST -0.01153 2.26634 -0.005 0.996
# TEMP -100.17340 77.75289 -1.288 0.198
#
# (Dispersion parameter for binomial family taken to be 1)
#
# Null deviance: 34.372 on 26 degrees of freedom
# Residual deviance: 21.594 on 20 degrees of freedom
# AIC: 35.594
confint.default(model.1) # based on asymptotic normality
confint(model.1) # based on profiling the least-squares estimation surface
model.2 <- glm(REMISS ~ LI, family="binomial")
summary(model.2)
# Estimate Std. Error z value Pr(>|z|)
# (Intercept) -3.777 1.379 -2.740 0.00615 **
# LI 2.897 1.187 2.441 0.01464 *
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#
# (Dispersion parameter for binomial family taken to be 1)
#
# Null deviance: 34.372 on 26 degrees of freedom
# Residual deviance: 26.073 on 25 degrees of freedom
# AIC: 30.073
plot(x=LI, y=REMISS,
panel.last = lines(sort(LI), fitted(model.2)[order(LI)]))
exp(coef(model.2)[2]) # odds ratio = 18.12449
exp(confint.default(model.2)[2,]) # 95% CI = (1.770284, 185.561725)
anova(model.2, test="Chisq")
# Df Deviance Resid. Df Resid. Dev Pr(>Chi)
# NULL 26 34.372
# LI 1 8.2988 25 26.073 0.003967 **
sum(residuals(model.2, type="deviance")^2) # 26.07296
model.2$deviance # 26.07296
sum(residuals(model.2, type="pearson")^2) # 23.93298
library(ResourceSelection)
hoslem.test(model.2$y, fitted(model.2), g=9)
# Hosmer and Lemeshow goodness of fit (GOF) test
# data: REMISS, fitted(model.2)
# X-squared = 7.3293, df = 7, p-value = 0.3954
1-model.2$deviance/model.2$null.deviance # "R-squared" = 0.2414424
plot(1:27, residuals(model.2, type="pearson"), type="b")
plot(1:27, residuals(model.2, type="deviance"), type="b")
summary(influence.measures(model.2))
# dfb.1_ dfb.LI dffit cov.r cook.d hat
# 8 0.63 -0.83 -0.93_* 0.88 0.58 0.15
hatvalues(model.2)[8] # 0.1498395
residuals(model.2)[8] # -1.944852
rstudent(model.2)[8] # -2.185013
cooks.distance(model.2)[8] # 0.5833219
detach(leukemia)
Disease outbreak (logistic regression)
- Load the disease outbreak data.
- Create interaction variables.
- Fit "full" logistic regression model of Disease vs four predictors and five interactions.
- Fit "reduced" logistic regression model of Disease vs four predictors.
- Conduct a likelihood ratio (or deviance) test for the five interactions.
- Display the analysis of deviance table with sequential deviances.
disease <- read.table("~/path-to-data/DiseaseOutbreak.txt", header=T)
attach(disease)
Age.Middle <- Age*Middle
Age.Lower <- Age*Lower
Age.Sector <- Age*Sector
Middle.Sector <- Middle*Sector
Lower.Sector <- Lower*Sector
model.1 <- glm(Disease ~ Age + Middle + Lower + Sector + Age.Middle + Age.Lower +
Age.Sector + Middle.Sector + Lower.Sector, family="binomial")
model.2 <- glm(Disease ~ Age + Middle + Lower + Sector, family="binomial")
anova(model.2, model.1, test="Chisq")
# Resid. Df Resid. Dev Df Deviance Pr(>Chi)
# 1 93 101.054
# 2 88 93.996 5 7.0583 0.2163
anova(model.1, test="Chisq")
# Df Deviance Resid. Df Resid. Dev Pr(>Chi)
# NULL 97 122.318
# Age 1 7.4050 96 114.913 0.006504 **
# Middle 1 1.8040 95 113.109 0.179230
# Lower 1 1.6064 94 111.502 0.205003
# Sector 1 10.4481 93 101.054 0.001228 **
# Age.Middle 1 4.5697 92 96.484 0.032542 *
# Age.Lower 1 1.0152 91 95.469 0.313666
# Age.Sector 1 1.1202 90 94.349 0.289878
# Middle.Sector 1 0.0001 89 94.349 0.993427
# Lower.Sector 1 0.3531 88 93.996 0.552339
detach(disease)
Toxicity and insects (logistic regression using event/trial data format)
- Load the toxicity data.
- Create a Survivals variable and a matrix with Deaths in one column and Survivals in the other column.
- Fit a logistic regression model of Deaths vs Dose.
- Calculate 95% confidence intervals for the regression parameters based on asymptotic normality and based on profiling the least-squares estimation surface.
- Calculate the odds ratio for Dose and a 95% confidence interval.
- Display the observed and fitted probabilities.
- Create a scatterplot of observed probabilities vs Dose and add a fitted line based on the logistic regression model.
toxicity <- read.table("~/path-to-data/toxicity.txt", header=T)
attach(toxicity)
Survivals <- SampSize - Deaths
y <- cbind(Deaths, Survivals)
model.1 <- glm(y ~ Dose, family="binomial")
summary(model.1)
# Estimate Std. Error z value Pr(>|z|)
# (Intercept) -2.64367 0.15610 -16.93 <2e-16 ***
# Dose 0.67399 0.03911 17.23 <2e-16 ***
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#
# (Dispersion parameter for binomial family taken to be 1)
#
# Null deviance: 383.0695 on 5 degrees of freedom
# Residual deviance: 1.4491 on 4 degrees of freedom
# AIC: 39.358
confint.default(model.1) # based on asymptotic normality
confint(model.1) # based on profiling the least-squares estimation surface
exp(coef(model.1)[2]) # odds ratio = 1.962056
exp(confint.default(model.1)[2,]) # 95% CI = (1.817279, 2.118366)
cbind(Dose, SampSize, Deaths, Deaths/SampSize, fitted(model.1))
# Dose SampSize Deaths
# 1 1 250 28 0.112 0.1224230
# 2 2 250 53 0.212 0.2148914
# 3 3 250 93 0.372 0.3493957
# 4 4 250 126 0.504 0.5130710
# 5 5 250 172 0.688 0.6739903
# 6 6 250 197 0.788 0.8022286
plot(x=Dose, y=Deaths/SampSize,
panel.last = lines(sort(Dose), fitted(model.1)[order(Dose)]))
detach(toxicity)