Find an F Critical Value
Find an F Critical ValueMinitab® – Procedure
You may need to find an F critical value if you are using the critical value approach to conduct a hypothesis test that uses an F-statistic.
- Select Calc >> Probability Distributions >> F...
- Click the button labeled Inverse cumulative probability. (Ignore the box labeled Noncentrality parameter. That is, leave the default value of 0.0 as is.)
- Type in the number of numerator degrees of freedom in the box labeled Numerator degrees of freedom.
- Type in the number of denominator degrees of freedom in the box labeled Denominator degrees of freedom.
- Click the button labeled Input Constant. In the box, type the cumulative probability for which you want to find the associated F-value.
- Select OK. The F-value will appear in the session window.
Example
Some researchers at UCLA conducted a study on cyanotic heart disease in children. They measured the age at which the child spoke his or her first word (x, in months) and the Gesell adaptive score (y) on a sample of 21 children.
Is there evidence of a relationship between age at first word and Gesell adaptive score? That is, should we reject the null hypothesis H0: β1 = 0 against the alternative hypothesis HA: β1 ≠ 0 at the 0.05 level? The resulting data (adaptive.txt) yield an ANOVA F-statistic of 13.20.
Minitab Dialog Box
Because the F-test is large regardless of whether the population slope is positive or negative, the F-test is always a one-sided test. Therefore, because we want to conduct the hypothesis test at the 0.05 level, the appropriate cumulative probability to enter is 0.95. The number of numerator degrees of freedom is always 1 for a simple linear regression model with one predictor. Because there are 21 measurements in the sample, the appropriate number of denominator degrees of freedom is 19. Therefore, your Minitab dialog box should look like:
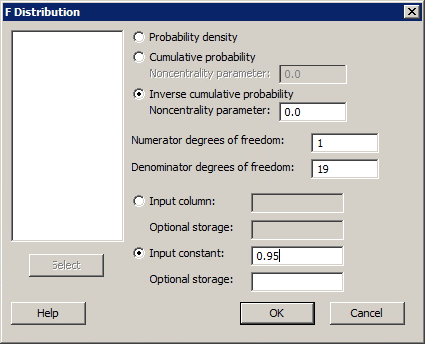
Sample Minitab Output
In this case, Minitab tells us that the F-critical value is:
Inverse Cumulative Distribution Function
F distribution with 1 DF in numerator and 19 DF in denominator
| P ( X ≤ x) | x |
|---|---|
| 0.95 | 4.38075 |