2.11 - The Lack of Fit F-test
2.11 - The Lack of Fit F-testInvestigating New Accounts Data
We're almost there! We just need to determine an objective way of deciding when too much of the error in our prediction is due to a lack of model fit. That's where the lack of fit F-test comes into play. Let's return to the first checking account example, (New Accounts data):
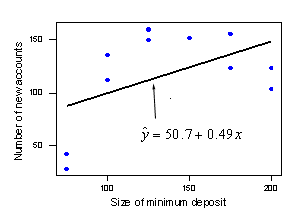
Jumping ahead to the punchline, here's Minitab's output for the lack of fit F-test for this data set:
Analysis of Variance
| Source | DF | Adj SS | Adj MS | F-Value | P-Value |
|---|---|---|---|---|---|
| Regression | 1 | 5141 | 5141 | 3.14 | 0.110 |
| Residual Error | 9 | 14742 | 1638 | ||
| Lack of Fit | 4 | 13594 | 3398 | 14.80 | 0.006 |
| Pure Error | 5 | 1148 | 230 | ||
| Total | 10 | 19883 |
1 row with no replicates
As you can see, the lack of fit output appears as a portion of the analysis of variance table. In the Sum of Squares ("SS") column, we see — as we previously calculated — that SSLF = 13594 and SSPE = 1148 sum to SSE = 14742. We also see in the Degrees of Freedom ("DF") column that — since there are n = 11 data points and c = 6 distinct x values (75, 100, 125, 150, 175, and 200) — the lack of fit degrees of freedom c - 2 = 4 and the pure error degrees of freedom is n - c = 5 sum to the error degrees of freedom n - 2 = 9.
Just as is done for the sums of squares in the basic analysis of variance table, the lack of fit sum of squares and the error sum of squares are used to calculate "mean squares." They are even calculated similarly, namely by dividing the sum of squares by their associated degrees of freedom. Here are the formal definitions of the mean squares:
In the Mean Squares ("MS") column, we see that the lack of fit mean square MSLF is 13594 divided by 4, or 3398. The pure error mean square MSPE is 1148 divided by 5, or 230:
Analysis of Variance
| Source | DF | Adj SS | Adj MS | F-Value | P-Value |
|---|---|---|---|---|---|
| Regression | 1 | 5141 | 5141 | 3.14 | 0.110 |
| Residual Error | 9 | 14742 | 1638 | ||
| Lack of Fit | 4 | 13594 | 3398 | 14.80 | 0.006 |
| Pure Error | 5 | 1148 | 230 | ||
| Total | 10 | 19883 |
You might notice that the lack of fit F-statistic is calculated by dividing the lack of fit mean square (MSLF = 3398) by the pure error mean square (MSPE = 230) to get 14.80. How do we know that this F-statistic helps us in testing the hypotheses:
- \(H_{0 }\): The relationship assumed in the model is reasonable, i.e., there is no lack of fit.
- \(H_{A }\): The relationship assumed in the model is not reasonable, i.e., there is a lack of fit.
The answer lies in the "expected mean squares." In our sample of n = 11 newly opened checking accounts, we obtained MSLF = 3398. If we had taken a different random sample of size n = 11, we would have obtained a different value for MSLF. Theory tells us that the average of all of the possible MSLF values we could obtain is:
\(E(MSLF) =\sigma^2+\dfrac{\sum n_i(\mu_i-(\beta_0+\beta_1X_i))^2}{c-2}\)
That is, we should expect MSLF, on average, to equal the above quantity — \(\sigma^{2}\) plus another messy-looking term. Think about that messy term. If the null hypothesis is true, i.e., if the relationship between the predictor x and the response y is linear, then \(\mu_{i} = \beta_{0} + \beta_{1}X_{i}\) and the messy term becomes 0 and goes away. That is, if there is no lack of fit, we should expect the lack of fit mean square MSLF to equal \(\sigma^{2}\).
What should we expect MSPE to equal? Theory tells us it should, on average, always equal \(\sigma^{2}\):
\(E(MSPE) =\sigma^2\)
Aha — there we go! The logic behind the calculation of the F-statistic is now clear:
- If there is a linear relationship between x and y, then \(\mu_{i} = \beta_{0} + \beta_{1}X_{i}\). That is, there is no lack of fit in the simple linear regression model. We would expect the ratio MSLF/MSPE to be close to 1.
- If there is not a linear relationship between x and y, then \(\mu_{i} ≠ \beta_{0} + \beta_{1}X_{i}\). That is, there is a lack of fit in the simple linear regression model. We would expect the ratio MSLF/MSPE to be large, i.e., a value greater than 1.
So, to conduct the lack of fit test, we calculate the value of the F-statistic:
\(F^*=\dfrac{MSLF}{MSPE}\)
and determine if it is large. To decide if it is large, we compare the F*-statistic to an F-distribution with c - 2 numerator degrees of freedom and n - c denominator degrees of freedom.
In summary
We follow standard hypothesis test procedures in conducting the lack of fit F-test. First, we specify the null and alternative hypotheses:
- \(H_{0}\): The relationship assumed in the model is reasonable, i.e., there is no lack of fit in the model \(\mu_{i} = \beta_{0} + \beta_{1}X_{i}\).
- \(H_{A}\): The relationship assumed in the model is not reasonable, i.e., there is lack of fit in the model \(\mu_{i} = \beta_{0} + \beta_{1}X_{i}\).
Second, we calculate the value of the F-statistic:
\(F^*=\dfrac{MSLF}{MSPE}\)
To do so, we complete the analysis of variance table using the following formulas.
Analysis of Variance
| Source | DF | SS | MS | F |
|---|---|---|---|---|
| Regression | 1 | \(SSR=\sum_{i=1}^{c}\sum_{j=1}^{n_i}(\hat{y}_{ij}-\bar{y})^2\) | \(MSR=\dfrac{SSR}{1}\) | \(F=\dfrac{MSR}{MSE}\) |
| Residual Error | n - 2 | \(SSE=\sum_{i=1}^{c}\sum_{j=1}^{n_i}(y_{ij}-\hat{y}_{ij})^2\) | \(MSE=\dfrac{SSE}{n-2}\) | |
| Lack of Fit | c - 2 | \(SSLF=\sum_{i=1}^{c}\sum_{j=1}^{n_i}(\bar{y}_{i}-\hat{y}_{ij})^2\) | \(MSLF=\dfrac{SSLF}{c-2}\) | \(F^*=\dfrac{MSLF}{MSPE}\) |
| Pure Error | n - c | \(SSPE=\sum_{i=1}^{c}\sum_{j=1}^{n_i}(y_{ij}-\bar{y}_{i})^2\) | \(MSPE=\dfrac{SSPE}{n-c}\) | |
| Total | n - 1 | \(SSTO=\sum_{i=1}^{c}\sum_{j=1}^{n_i}(y_{ij}-\bar{y})^2\) |
In reality, we let statistical software such as Minitab, determine the analysis of variance table for us.
Third, we use the resulting F*-statistic to calculate the P-value. As always, the P-value is the answer to the question "how likely is it that we’d get an F*-statistic as extreme as we did if the null hypothesis were true?" The P-value is determined by referring to an F-distribution with c - 2 numerator degrees of freedom and n - c denominator degrees of freedom.
Finally, we make a decision:
- If the P-value is smaller than the significance level \(\alpha\), we reject the null hypothesis in favor of the alternative. We conclude that "there is sufficient evidence at the \(\alpha\) level to conclude that there is a lack of fit in the simple linear regression model."
- If the P-value is larger than the significance level \(\alpha\), we fail to reject the null hypothesis. We conclude "there is not enough evidence at the \(\alpha\) level to conclude that there is a lack of fit in the simple linear regression model."
For our checking account example:

in which we obtain:
Analysis of Variance
| Source | DF | Adj SS | Adj MS | F-Value | P-Value |
|---|---|---|---|---|---|
| Regression | 1 | 5141 | 5141 | 3.14 | 0.110 |
| Residual Error | 9 | 14742 | 1638 | ||
| Lack of Fit | 4 | 13594 | 3398 | 14.80 | 0.006 |
| Pure Error | 5 | 1148 | 230 | ||
| Total | 10 | 19883 |
the F*-statistic is 14.80 and the P-value is 0.006. The P-value is smaller than the significance level \(\alpha = 0.05\) — we reject the null hypothesis in favor of the alternative. There is sufficient evidence at the \(\alpha = 0.05\) level to conclude that there is a lack of fit in the simple linear regression model. In light of the scatterplot, the lack of fit test provides the answer we expected.
Try it!
The lack of fit test
Fill in the missing numbers (??) in the following analysis of variance table resulting from a simple linear regression analysis.
Click on the light bulb
| Source | DF | Adj SS | Adj MS | F-Value | P-Value |
|---|---|---|---|---|---|
| Regression | ?? | 12.597 | ?? | ?? | 0.000 |
| Residual Error | ?? | ?? | ?? | ||
| Lack of Fit | 3 | ?? | ?? | ?? | ?? |
| Pure Error | ?? | 0.157 | ?? | ||
| Total | 14 | 15.522 |