1.10 - Further Examples
1.10 - Further ExamplesExample 1-6: Teen Birth Rate and Poverty Level Data
This dataset of size n = 51 is for the 50 states and the District of Columbia in the United States (Poverty data). The variables are y = the year 2002 birth rate per 1000 females 15 to 17 years old and x = poverty rate, which is the percent of the state’s population living in households with incomes below the federally defined poverty level. (Data source: Mind On Statistics, 3rd edition, Utts and Heckard).
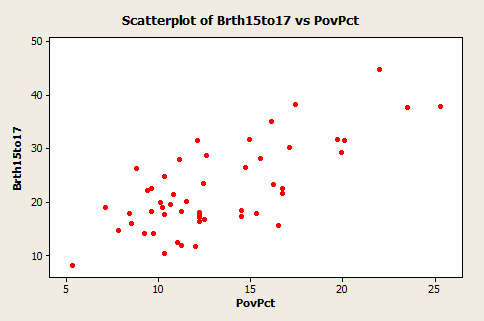
The plot of the data below (birth rate on the vertical) shows a generally linear relationship, on average, with a positive slope. As the poverty level increases, the birth rate for 15 to 17-year-old females tends to increase as well.
The figure below, created in Minitab using Stat >> Regression >> Fitted Line Plot, shows a regression line superimposed on the data. The equation is given near the top of the plot. Minitab should have written that the equation is for the “average” birth rate (or “predicted” birth rate would be okay too) because a regression equation describes the average value of y as a function of one or more x-variables. In statistical notation, the equation could be written \(\hat{y} = 4.267 + 1.373x \).
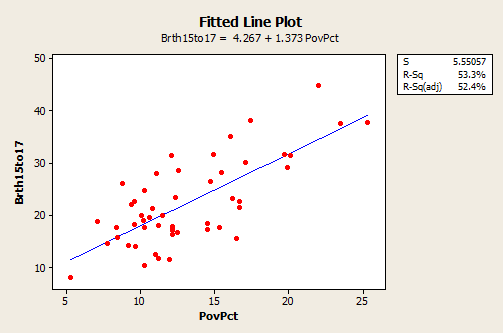
- The interpretation of the slope (value = 1.373) is that the 15 to 17-year-old birth rate increases by 1.373 units, on average, for each unit (one percent) increase in the poverty rate.
- The interpretation of the intercept (value=4.267) is that if there were states with a poverty rate = 0, the predicted average for the 15 to 17-year-old birth rate would be 4.267 for those states. Since there are no states with a poverty rate = 0 this interpretation of the intercept is not practically meaningful for this example.
In the graph with a regression line present, we also see the information that s = 5.55057 and \(R^{2}\) = 53.3%.
- The value of s tells us roughly the average difference between the y-values of individual observations and predictions of y based on the regression line.
- The value of \(R^{2}\) can be interpreted to mean that poverty rates "explain" 53.3% of the observed variation in the 15 to 17-year-old average birth rates of the states.
The \(R^{2}\) (adj) value (52.4%) is an adjustment to \(R^{2}\) based on the number of x-variables in the model (only one here) and the sample size. With only one x-variable, the adjusted \(R^{2}\) is not important.
Example 1-7: Lung Function in 6 to 10 Year Old Children
The data are from n = 345 children between 6 and 10 years old. The variables are y = forced exhalation volume (FEV), a measure of how much air somebody can forcibly exhale from their lungs, and x = age in years. (Data source: The data here are a part of a dataset given in Kahn, Michael (2005). "An Exhalent Problem for Teaching Statistics", The Journal of Statistical Education, 13(2).
Below is a plot of the data with a simple linear regression line superimposed. The plot was done in Minitab and as pointed out earlier, the word “average” should come before the y-variable name.
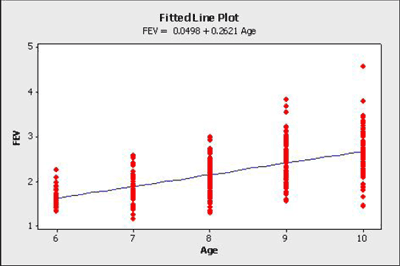
- The estimated regression equation is that average \(FEV = 0.0498 + 0.2621 \times age\). For instance, for an 8 year old we can use the equation to estimate that the average \(FEV = 0.0498 + 0.2621 \times (8) = 2.1466\).
- The interpretation of the slope is that the average FEV increases by 0.2621 for each one-year increase in age (in the observed age range).
An interesting and possibly important feature of these data is that the variance of individual y-values from the regression line increases as age increases. This feature of data is called non-constant variance. For example, the FEV values of 10-year-olds are more variable than the FEV values of 6-year-olds. This is seen by looking at the vertical ranges of the data in the plot. This may lead to problems using a simple linear regression model for these data, which is an issue we'll explore in more detail in Lesson 4.
Above, we only analyzed a subset of the entire dataset. The full dataset (FEV Data) is shown in the plot below:
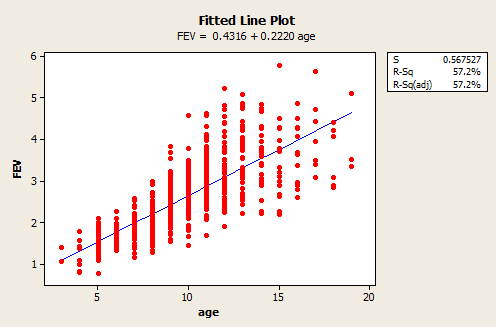
As we can see, the range of ages now spans 3 to 19 years old and the estimated regression equation is FEV = 0.4316 + 0.2220 × age. Both the slope and intercept have noticeably changed, but the variance still appears to be non-constant. This illustrates that it is important to be aware of how you are analyzing your data. If you only use a subset of your data that spans a shorter range of predictor values, then you could obtain noticeably different results than if you had used the full dataset.