Lesson 11: Response Surface Methods and Designs
Lesson 11: Response Surface Methods and DesignsOverview of Response Surface Methods
We are now going to shift from screening designs where the primary focus of previous lessons was factor screening – (two-level factorials, fractional factorials being widely used), to trying to optimize an underlying process and look for the factor level combinations that give us the maximum yield and minimum costs. In many applications, this is our goal. However in some cases we are trying to hit a target or aim to match some given specifications - but this brings up other issues which we will get to later.
RSM as a Sequential Process
Here the objective of Response Surface Methods (RSM) is optimization, finding the best set of factor levels to achieve some goal. This lesson aims to cover the following goals:
The text has a graphic depicting a response surface method in three dimensions, though actually it is four dimensional space that is being represented since the three factors are in 3-dimensional space the the response is the 4th dimension.
Instead, let's look at 2 dimensions - this is easier to think about and visualize. There is a response surface and we will imagine the ideal case where there is actually a 'hill' which has a nice centered peak. (If only reality were so nice, but it usually isn't!). Consider the geologic ridges that exist here in central Pennsylvania, the optimum or highest part of the 'hill' might be anywhere along this ridge. There's no clearly defined centered high point or peak that stands out. In this case there would be a whole range of values of \(x_{1}\) and \(x_{2}\) that would all describe the same 'peak' -- actually the points lying along the top of the ridge. This type of situation is quite realistic where there does not exist a predominate optimum.
But for our purposes let's think of this ideal 'hill' and the problem is that you don't know where this is and you want to find factor level values where the response is at its peak. This is your quest, to find the values \(x_{1}^{optimum}\) and \(x_{2}^{optimum}\), where the response is at its peak. You might have a hunch that the optimum exists in certain location. This would be good area to start - some set of conditions, perhaps the way that the factory has always been doing things - and then perform an experiment at this starting point.
The actual variables in their natural units of measurement are used in the experiment. However, when we design our experiment we will use our coded variables, \(x_{1}\) and \(x_{2}\) which will be centered on 0, and extend +1 and -1 from the center of the region of experimentation. Therefore, we will take our natural units and then center and rescale them to the range from -1 to +1.
Our goal is to start somewhere using our best prior or current knowledge and search for the optimum spot where the response is either maximized or minimized.
Here are the models that we will use.
Screening Response Model
\(y = \beta_{0} + \beta_{1} x_{1} + \beta_{2} x_{2} + \beta_{12} x_{1} x_{2} + \varepsilon\)
The screening model that we used for the first order situation involves linear effects and a single cross product factor, which represents the linear x linear interaction component.
Steepest Ascent Model
If we ignore cross products which gives an indication of the curvature of the response surface that we are fitting and just look at the first order model this is called the steepest ascent model:
\(y=\beta_{0} + \beta_{1} x_{1} + \beta_{2} x_{2} + \varepsilon\)
Optimization Model
Then, when we think that we are somewhere near the 'top of the hill' we will fit a second order model. This includes in addition the two second-order quadratic terms.
\(y=\beta_{0} + \beta_{1} x_{1} + \beta_{2} x_{2} + \beta_{12} x_{1} x_{2} + \beta_{11} x_{1}^2 + \beta_{22} x_{2}^2 + \varepsilon\)
Steepest Ascent - The First Order Model
Let's look at the first order situation - the method of steepest ascent. Now, remember, in the first place we don't know if the 'hill' even exists so we will start somewhere where we think the optimum exists. We start somewhere in terms of the natural units and use the coded units to do our experiment. Consider the example 11.1 in the textbook. We want to start in the region where \(x_{1} = \) reaction time (30 - 40 seconds) and \(x_{2} = \) temperature (150 - 160 degrees), and we want to look at the yield of the process as a function of these factors. In a sense, for the purpose of illustrating this concept, we can superimpose this region of experimentation on to our plot of our unknown 'hill'. We obviously conduct the experiment in its natural units but the designs will be specified in the coded units so we can apply them to any situation.
Specifically, here we use a design with four corner points, a \(2^2\) design and five center points. We now fit this first-order model and investigate it.
We put in the actual data for A and B and the response measurements Y.
We fit a full model first: See: Ex-11-1-output.doc
We fit the surface. The model has two main effects, one cross product term and then one additional parameter as the mean for the center point. The residuals in this case have four \(df\) which come from replication of the center points. Since there are five center points, i.e., four \(df\) among the five center points. This is a measure of pure error.
We start by testing for curvature. The question is whether the mean of the center points is different from the values at \(x_{1},x_{2} = (0,0)\) predicted from the screening response model (main effects plus interaction). We are testing whether the mean of the points at the center are on the plane fit by the four corner points. If the p-value had been small, this would have told you that a mean of the center points is above or below the plane indicating curvature in the response surface. The fact that, in this case, it is not significant indicates there is no curvature. Indeed the center points fall exactly on the plane that fits the quarter points.
There is just one degree of freedom for this test because the design only has one additional location in terms of the x's.
Next we check for significant effects of the factors. We see from the ANOVA that there is no interaction. So, let's refit this model without the interaction term, leaving just the A and B terms. We still have the average of the center points and our AOV now shows \(5\ df\) for residual error. One of these is lack of fit of the additive model and there are \(4\ df\) of pure error as before. We have \(1\ df\) for curvature, and lack of fit in this case is just the interactions from the model.
What do we do with this? See the Minitab analysis and redo these results in EX11-1.mpx | Ex11-1.csv
Our estimated model is: \(\hat{y} = 40.34 + 0.775x_{1} + 0.325x_{2}\)
So, for any \(x_{1}\) and \(x_{2}\) we can predict \(y\). This fits a flat surface and it tells us that the predicted \(y\) is a function of \(x_{1}\) and \(x_{2}\) and the coefficients are the gradient of this function. We are working in coded variables at this time so these coefficients are unitless.
If we move 0.775 in the direction of \(x_{1}\) and then 0.325 in the direction of \(x_{2}\) this is the direction of steepest ascent. All we know is that this flat surface is one side of the 'hill'.
The method of steepest ascent tells us to do a first order experiment and find the direction that the 'hill' goes up and start marching up the hill taking additional measurements at each \((x_{1}, x_{2})\) until the response starts to decrease. If we start at 0, in coded units, then we can do a series of single experiments on this path up the 'hill' of the steepest descent. If we do this at a step size of \(x_{1} = 1\), then:
\(1\ /\ 0.775 = x_{2}\ /\ 0.325 \rightarrow x_{2} = 0.325\ /\ 0.775 = 0.42 \)
and thus our step size of \(x_{1} = 1\) determines that \(x_{2} = 0.42\), in order to move in the direction determined to be the steepest ascent. If we take steps of 1 in coded units, this would be five minutes in terms of the time units. And for each step along that path, we would go up 0.42 coded units in \(x_{2}\) or approximately 2º on the temperature scale.
| Steps | Coded Variables | Natural Variables | Treatment Total | ||
|---|---|---|---|---|---|
| \(x_1\) | \(x_1\) | \(\xi_1\) | \(\xi_1\) | y | |
| Origin | 0 | 0 | 35 | 155 | |
| \( \Delta\) | 1.00 | 0.42 | 5 | 2 | |
| Origin + \( \Delta\) | 1.00 | 0.42 | 40 | 157 | 41.0 |
| Origin + \(2 \Delta\) | 2.00 | 0.84 | 45 | 159 | 42.9 |
| Origin + \(3 \Delta\) | 3.00 | 1.26 | 50 | 161 | 47.1 |
| Origin + \(4 \Delta\) | 4.00 | 1.68 | 55 | 163 | 49.7 |
| Origin + \(5 \Delta\) | 5.00 | 2.10 | 60 | 165 | 53.8 |
| Origin + \(6 \Delta\) | 6.00 | 2.52 | 65 | 167 | 59.9 |
| Origin + \(7 \Delta\) | 7.00 | 2.94 | 70 | 169 | 65.0 |
| Origin + \(8 \Delta\) | 8.00 | 3.36 | 75 | 171 | 70.4 |
| Origin + \(9 \Delta\) | 9.00 | 3.78 | 80 | 173 | 77.6 |
| Origin + \(10 \Delta\) | 10.00 | 4.20 | 85 | 175 | 80.3 |
| Origin + \(11 \Delta\) | 11.00 | 4.62 | 90 | 179 | 76.2 |
| Origin + \(12 \Delta\) | 12.00 | 5.04 | 95 | 181 | 75.1 |
| Table 11-3 Steepest Ascent Experiment for Example 11-1 | |||||
Here is the series of steps in additional measures of five minutes and 2º temperature. The response is plotted and shows an increase that drops off towards the end.
This is a pretty smooth curve and in reality, you probably should go a little bit more beyond the peak to make sure you are at the peak. But all you are trying to do is to find out approximately where the top of the 'hill' is. If your first experiment is not exactly right you might have gone off in the wrong direction!
So you might want to do another first-order experiment just to be sure. Or, you might wish to do a second order experiment, assuming you are near the top. This is what we will discuss in the next section. The second order experiment will help find a more exact location of the peak.
The point is, this is a fairly cheap way to 'scout around the mountain' to try to find where the optimum conditions are. Remember, this example is being shown in two dimensions but you may be working in three or four-dimensional space! You can use the same method, fitting a first-order model and then moving up the response surface in k dimensional space until you think you are close to where the optimal conditions are.
If you are in more than 2 dimensions, you will not be able to get a nice plot. But that is OK. The method of steepest ascent tells you where to take new measurements, and you will know the response at those points. You might move a few steps and you may see that the response continued to move up or perhaps not - then you might do another first order experiment and redirect your efforts. The point is, when we do the experiment for the second order model, we hope that the optimum will be in the range of the experiment - if it is not, we are extrapolating to find the optimum. In this case, the safest thing to do is to do another experiment around this estimated optimum. Since the experiment for the second order model requires more runs than experiments for the first order model, we want to move into the right region before we start fitting second-order models.
Steepest Ascent - The Second Order Model
\(y = \beta_{0} + \beta_{1} x_{1} + \beta_{2} x_{2} + \beta_{12} x_{1} x_{2} + \beta_{11} x_{1}^2 + \beta_{22} x_{2}^2 + \varepsilon\)
This second order model includes linear terms, cross product terms and a second order term for each of the x's. If we generalize this to \(k\) x's, we have \(k\) first order terms, \(k\) second order terms and then we have all possible pairwise first-order interactions. The linear terms just have one subscript. The quadratic terms have two subscripts. There are \(k * \dfrac{(k - 1)}{2}\) interaction terms. To fit this model, we are going to need a response surface design that has more runs than the first order designs used to move close to the optimum.
This second order model is the basis for response surface designs under the assumption that although the hill is not a perfect quadratic polynomial in k dimensions, it provides a good approximation to the surface near the maximum or a minimum.
Assuming that we have 'marched up this hill' and if we re-specified the region of interest in our example, we are now between 80 - 90 in terms of time and 170 - 180 in terms of temperature. We would now translate these natural units into our coded units and if we fit the first order model again, hopefully we can detect that the middle is higher than the corner points so we would have curvature in our model, and could now fit a quadratic polynomial.
After using the Steepest Ascent method to find the optimum location in terms of our factors, we can now go directly to the second order response surface design. A favorite design that we consider is sometimes referred to as a central composite design. The central compositive design is shown on Figure 11.3 above and in more detail in the text in Figure 11.10. The idea is simple - take the \(2^k\) corner points, add a center point, and then create a star by drawing a line through the center point orthogonal to each face of the hypercube. Pick a radius along this line and place a new point at that radius. The effect is that each factor is now measured at 5 levels - center, 2 corners and the 2 star points. This gives us plenty of unique treatments to fit the 2nd order model with treatment degrees of freedom left over to test the goodness of fit. Replication is still usually done only at the center point.
Objectives
- Response Surface Methodology and its sequential nature for optimizing a process
- First order and second order response surface models and how to find the direction of steepest ascent (or descent) to maximize (or minimize) the response
- How to deal with several responses simultaneously (Multiple Response Optimization)
- Central Composite Designs (CCD) and Box-Behnken Designs as two of the major Response Surface Designs and how two generate them using Minitab
- Design and Analysis of Mixture Designs for cases where the sum of the factor levels equals a constant, i.e. 100% or the totality of the components
- Introductory understanding of designs for computer models
RSM dates from the 1950's. Early applications were found in the chemical industry. We have already talked about Box. Box and Draper have some wonderful references about building RSMs and analyzing them which are very useful.
11.1 - Multiple Responses
11.1 - Multiple ResponsesIn many experiments more than one response is of interest for the experimenter. Furthermore, we sometimes want to find a solution for controllable factors which result in the best possible value for each response. This is the context of multiple response optimization, where we seek a compromise between the responses; however, it is not always possible to find a solution for controllable factors which optimize all of the responses simultaneously. Multiple response optimization has an extensive literature in the context of multiple objective optimization which is beyond the scope of this course. Here, we will discuss the basic steps in this area.
As expected, multiple response analysis starts with building a regression model for each response separately. For instance, in Example 11.2 we can fit three different regression models for each of the responses which are Yield, Viscosity and Molecular Weight based on two controllable factors: Time and Temperature.
One of the traditional methods way to analyze and find the desired operating condition one is overlaid contour plots. This method is mainly useful when we have two or maybe three controllable factors but in higher dimensions it loses its efficiency. This method simply consists of overlaying contour plot for each of the responses one over another in the controllable factors space and finding the area which makes the best possible value for each of the responses. Figure 11.16 (Montgomery, 7th Edition) shows the overlaid contour plots for example 11.2 in Time and Temperature space.
The unshaded area is where yield > 78.5, 62 < viscosity < 68, and molecular weight < 3400. This area might be of special interest for the experimenter because they satisfy given conditions on the responses.
Another dominant approach for dealing with multiple response optimization is to form a constrained optimization problem. In this approach we treat one of the responses as the objective of a constrained optimization problem and other responses as the constraints where the constraint’s boundary is to be determined by the decision maker (DM). The Design-Expert software package solves this approach using a direct search method.
Another important procedure that we will discuss here, also implemented in Minitab, is the desirability function approach. In this approach the value of each response for a given combination of controllable factors is first translated to a number between zero and one known as individual desirability. Individual desirability functions are different for different objective types which might be Maximization, Minimization or Target. If the objective type is maximum value, the desirability function is defined as
\(d=\left\{\begin{array}
{cl}
0 & y<L \\ \left(\frac{y-L}{T-L}\right)^r & L\leq y\leq T \\ 1 & y>T
\end{array} \right. \)
When the objective type is a minimum value the, the individual desirability is defines as
\(d=\left\{\begin{array}
{cl}
1 & y<T \\ \left(\frac{U-y}{U-T}\right)^r & T\leq y\leq U \\ 0 & y>U
\end{array} \right. \)
Finally the two-sided desirability function with target-the-best objective type is defined as
\(d=\left\{\begin{array}
{cl}
0 & y<L \\ \left(\frac{y-L}{T-L}\right)^{r_1} & L\leq y\leq T \\ \left(\frac{U-y}{U-T}\right)^{r_2} & T\leq y\leq U \\ 0 & y>U
\end{array} \right. \)
Where the \(r_1\) , \(r_2\) and r define the shape of the individual desirability function (Figure 11.17 in the text shows the shape of individual desirability for different values of shape parameter). Individual desirability is then used to calculate the overall desirability using the following formula:
\(D=(d_1 d_2 \ldots d_m)^{1/m}\)
where m is the number of responses. Now, the design variables should be chosen so that the overall desirability will be maximized. Minitab’s Stat > DOE > Response Surface > Response Optimizer routine uses the desirability approach to optimize several responses, simultaneously.
11.2 - Response Surface Designs
11.2 - Response Surface DesignsAfter using the Steepest Ascent method to find the optimum location in terms of our factors, we can now go directly to the second order response surface design. A favorite design that we consider for a second order model is referred to as a central composite design.
Here is an example in two dimensions: Example 11.2 in the text. We have \(2^k\) corner points and we have some number of center points which generally would be somewhere between 4 and 7, (five here). In two dimensions there are 4 star points, but in general there are \(2^k\) star points in \(k\) dimensions. The value of these points is something greater than 1. Why is it something greater than 1? If you think about the region of experimentation, we have up to now always defined a box, but if you think of a circle the star points are somewhere on the circumference of that circle, or in three dimensions on the ball enclosing the box. All of these are design points around the region where you expect the optimum outcome to be located. Typically the only replication, in order to get some measure of pure error, is done at the center of the design.
The data set for the Example 11.2 is found in the Minitab worksheet, Ex11-2.mwx | Ex11-2.csv. The analysis using the Response Surface Design analysis module is shown in the Ex11-2.mpx.
11.2.1 - Central Composite Designs
11.2.1 - Central Composite DesignsIn the last section we looked at the Example 11.2 which was in coded variables and was a central composite design.
In this section we examine a more general central composite design. For \(k = 2\) we had a \(2^2\) design with center points, which was required for our first order model; then we added \(2*k\) star points. The star or axial points are, in general, at some value \(\alpha\) and \({-\alpha}\) on each axis.
There are various choices of α. If \(\alpha = 1\), the star points would be right on the boundary, and we would just have a \(3^2\) design. Thus \(\alpha = 1\) is a special case, a case that we considered in the \(3^k\) designs. A more common choice of \(\alpha\) is \(\alpha =\sqrt{k}\) which gives us a spherical design as shown below.
Our \(2^2\) design gives us the box, and adding the axial points (in green) outside of the box gives us a spherical design where \(\alpha =\sqrt{k}\). The corner points and the axial points at \(\alpha\), are all points on the surface of a ball in three dimensions, as we see below.
This design in \(k = 3\) dimensions can also be referred to as a central composite design, chosen so that the design is spherical. This is a common design. Much of this detail is given in Table 11.11 of the text.
An alternative choice where \(\alpha = \left ( n_{F} \right )^{\frac{1}{4}}\), or the fourth root of the number of points in the factorial part of the design, gives us a rotatable design.
If we have k factors, then we have, \(2^k\) factorial points, \(2*k\) axial points and \(n_{c}\) center points. Below is a table that summarizes these designs and compares them to \(3^k\) designs:
| k = 2 | k = 3 | k = 4 | k = 5 | ||
|---|---|---|---|---|---|
| Central Composite Designs | Factorial points \(\mathbf{2^k}\) | 4 | 8 | 16 | 32 |
| Star points \(\mathbf{2^k}\) | 4 | 6 | 8 | 10 | |
| Center points \(\mathbf{n_c}\) (varies) | 5 | 5 | 6 | 6 | |
| Total | 13 | 19 | 30 | 48 | |
| \(\mathbf{3^k}\) Designs | 9 | 27 | 81 | 243 | |
| Choice of \(\alpha\) | Spherical design ( \(\mathbf{\alpha =\sqrt{k}}\) ) | 1.4 | 1.73 | 2 | 2.24 |
| Rotatable design ( \(\mathbf{\alpha = \left ( n_{F} \right )^{\frac{1}{4}}}\) ) | 1.4 | 1.68 | 2 | 2.38 | |
Compare the total number of observations required in the central composite designs versus the \(3^k\) designs. As the number of factors increases, you can see the efficiencies that are brought to bear.
The spherical designs are rotatable in the sense that the points are all equidistant from the center. Rotatable refers to the variance of the response function. A rotatable design exists when there is an equal prediction variance for all points a fixed distance from the center, 0. This is a nice property. If you pick the center of your design space and run your experiments, all points that are equal distance from the center in any direction, have an equal variance of prediction.
You can see in the table above that the difference in the variation between the spherical and rotatable designs are slight, and don't seem to make much difference. But both ideas provide justification for selecting how far away the star points should be from the center.
Why do we take about five or six center points in the design? The reason is also related to the variance of a predicted value. When fitting a response surface you want to estimate the response function in this design region where we are trying to find the optimum. We want the prediction to be reliable throughout the region, and especially near the center since we hope the optimum is in the central region. By picking five to six center points, the variance in the middle is approximately the same as the variance at the edge. If you only had one or two center points, then you would have less precision in the middle than you would have at the edge. As you go farther out beyond a distance of 1 in coded units, you get more variance and less precision. What we are trying to do is to balance the precision at the edge of the design relative to the middle.
How do you select the region where you want to run the experiment? Remember, for each factor X we said we need to choose the lower level is and the upper level for the region of experimentation. We usually picked the -1 and 1 as the boundary. If the lower natural unit is really the lowest number that you can test, because the experiment won't work lower than this, or the lower level is zero and you can't put in a negative amount of something, then, the star point is not possible because it is outside the range of experimentation.
If this is the case, one choice that you could make would be to use the \({-\alpha}\) as the lowest point. Generally, if you are not up against a boundary then this is not an issue and the star points are a way to reach beyond the region that you think the experiment should be run in. The issue isn't selecting the coding of the design relative to the natural units. You might lose some of these exact properties, but as long as you have the points nicely spread out in space you can fit a regression function. The penalty for not specifying the points exactly would be seen in the variance, and it would be actually very slight.
Minitab® – Generating These Designs in Minitab
Minitab will show you the available designs and how to generate these designs.
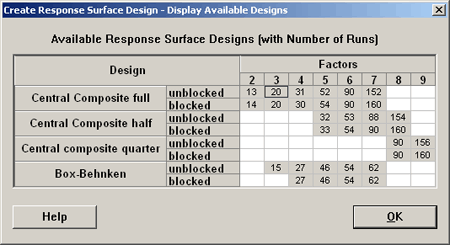
We can create central composite designs using a full factorial, central composite designs with fractional factorials, half fraction and a quarter fraction, and they can be arranged in blocks. Later, we will look at the Box-Behnken designs.
As an example, we look at the \(k=3\) design, set up in Minitab using a full factorial, completely randomized, in two blocks, or three blocks with six center points and the default \(\alpha = 1.633\) (or \(\alpha = 1.682\) for a rotatable design).
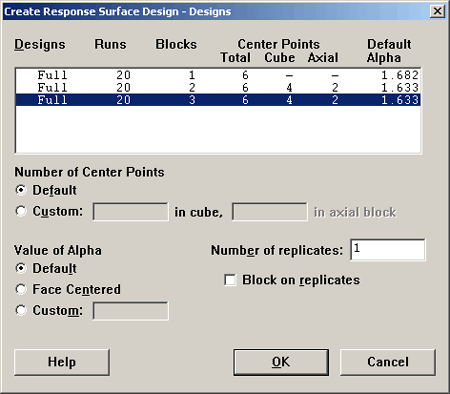
If you do not want the default \(\alpha\) you can specify your own in the lower left. A Face Centered design is obtained by putting the \(\alpha\) at +1 and -1 on the cube. Here is the design that results:
| Run | Blk | A | B | C |
|---|---|---|---|---|
| 1 | 1 | -1.000 | -1.000 | -1.000 |
| 2 | 1 | 1.000 | 1.000 | -1.000 |
| 3 | 1 | 1.000 | -1.000 | 1.000 |
| 4 | 1 | -1.000 | 1.000 | 1.000 |
| 5 | 1 | 0.000 | 0.000 | 0.000 |
| 6 | 1 | 0.000 | 0.000 | 0.000 |
| 7 | 2 | 1.000 | -1.000 | -1.000 |
| 8 | 2 | -1.000 | 1.000 | -1.000 |
| 9 | 2 | -1.000 | -1.000 | 1.000 |
| 10 | 2 | 1.000 | 1.000 | 1.000 |
| 11 | 2 | 0.000 | 0.000 | 0.000 |
| 12 | 2 | 0.000 | 0.000 | 0.000 |
| 13 | 3 | -1.633 | 0.000 | 0.000 |
| 14 | 3 | 1.633 | 0.000 | 0.000 |
| 15 | 3 | 0.000 | -1.633 | 0.000 |
| 16 | 3 | 0.000 | 1.633 | 0.000 |
| 17 | 3 | 0.000 | 0.000 | -1.633 |
| 18 | 3 | 0.000 | 0.000 | 1.633 |
| 19 | 3 | 0.000 | 0.000 | 0.000 |
| 20 | 3 | 0.000 | 0.000 | 0.000 |
| Run | Blk | A | B | C |
|---|---|---|---|---|
| 1 | 1 | -1.000 | -1.000 | -1.000 |
| 2 | 1 | 1.000 | 1.000 | -1.000 |
| 3 | 1 | 1.000 | -1.000 | 1.000 |
| 4 | 1 | -1.000 | 1.000 | 1.000 |
| 5 | 1 | 0.000 | 0.000 | 0.000 |
| 6 | 1 | 0.000 | 0.000 | 0.000 |
| 7 | 2 | 1.000 | -1.000 | -1.000 |
| 8 | 2 | -1.000 | 1.000 | -1.000 |
| 9 | 2 | -1.000 | -1.000 | 1.000 |
| 10 | 2 | 1.000 | 1.000 | 1.000 |
| 11 | 2 | 0.000 | 0.000 | 0.000 |
| 12 | 2 | 0.000 | 0.000 | 0.000 |
| 13 | 3 | -1.633 | 0.000 | 0.000 |
| 14 | 3 | 1.633 | 0.000 | 0.000 |
| 15 | 3 | 0.000 | -1.633 | 0.000 |
| 16 | 3 | 0.000 | 1.633 | 0.000 |
| 17 | 3 | 0.000 | 0.000 | -1.633 |
| 18 | 3 | 0.000 | 0.000 | 1.633 |
| 19 | 3 | 0.000 | 0.000 | 0.000 |
| 20 | 3 | 0.000 | 0.000 | 0.000 |
| Run | Blk | A | B | C |
|---|---|---|---|---|
| 1 | 1 | -1.000 | -1.000 | -1.000 |
| 2 | 1 | 1.000 | 1.000 | -1.000 |
| 3 | 1 | 1.000 | -1.000 | 1.000 |
| 4 | 1 | -1.000 | 1.000 | 1.000 |
| 5 | 1 | 0.000 | 0.000 | 0.000 |
| 6 | 1 | 0.000 | 0.000 | 0.000 |
| 7 | 2 | 1.000 | -1.000 | -1.000 |
| 8 | 2 | -1.000 | 1.000 | -1.000 |
| 9 | 2 | -1.000 | -1.000 | 1.000 |
| 10 | 2 | 1.000 | 1.000 | 1.000 |
| 11 | 2 | 0.000 | 0.000 | 0.000 |
| 12 | 2 | 0.000 | 0.000 | 0.000 |
| 13 | 3 | -1.633 | 0.000 | 0.000 |
| 14 | 3 | 1.633 | 0.000 | 0.000 |
| 15 | 3 | 0.000 | -1.633 | 0.000 |
| 16 | 3 | 0.000 | 1.633 | 0.000 |
| 17 | 3 | 0.000 | 0.000 | -1.633 |
| 18 | 3 | 0.000 | 0.000 | 1.633 |
| 19 | 3 | 0.000 | 0.000 | 0.000 |
| 20 | 3 | 0.000 | 0.000 | 0.000 |
| Run | Blk | A | B | C |
|---|---|---|---|---|
| 1 | 1 | -1.000 | -1.000 | -1.000 |
| 2 | 1 | 1.000 | 1.000 | -1.000 |
| 3 | 1 | 1.000 | -1.000 | 1.000 |
| 4 | 1 | -1.000 | 1.000 | 1.000 |
| 5 | 1 | 0.000 | 0.000 | 0.000 |
| 6 | 1 | 0.000 | 0.000 | 0.000 |
| 7 | 2 | 1.000 | -1.000 | -1.000 |
| 8 | 2 | -1.000 | 1.000 | -1.000 |
| 9 | 2 | -1.000 | -1.000 | 1.000 |
| 10 | 2 | 1.000 | 1.000 | 1.000 |
| 11 | 2 | 0.000 | 0.000 | 0.000 |
| 12 | 2 | 0.000 | 0.000 | 0.000 |
| 13 | 3 | -1.633 | 0.000 | 0.000 |
| 14 | 3 | 1.633 | 0.000 | 0.000 |
| 15 | 3 | 0.000 | -1.633 | 0.000 |
| 16 | 3 | 0.000 | 1.633 | 0.000 |
| 17 | 3 | 0.000 | 0.000 | -1.633 |
| 18 | 3 | 0.000 | 0.000 | 1.633 |
| 19 | 3 | 0.000 | 0.000 | 0.000 |
| 20 | 3 | 0.000 | 0.000 | 0.000 |
| Run | Blk | A | B | C |
|---|---|---|---|---|
| 1 | 1 | -1.000 | -1.000 | -1.000 |
| 2 | 1 | 1.000 | 1.000 | -1.000 |
| 3 | 1 | 1.000 | -1.000 | 1.000 |
| 4 | 1 | -1.000 | 1.000 | 1.000 |
| 5 | 1 | 0.000 | 0.000 | 0.000 |
| 6 | 1 | 0.000 | 0.000 | 0.000 |
| 7 | 2 | 1.000 | -1.000 | -1.000 |
| 8 | 2 | -1.000 | 1.000 | -1.000 |
| 9 | 2 | -1.000 | -1.000 | 1.000 |
| 10 | 2 | 1.000 | 1.000 | 1.000 |
| 11 | 2 | 0.000 | 0.000 | 0.000 |
| 12 | 2 | 0.000 | 0.000 | 0.000 |
| 13 | 3 | -1.633 | 0.000 | 0.000 |
| 14 | 3 | 1.633 | 0.000 | 0.000 |
| 15 | 3 | 0.000 | -1.633 | 0.000 |
| 16 | 3 | 0.000 | 1.633 | 0.000 |
| 17 | 3 | 0.000 | 0.000 | -1.633 |
| 18 | 3 | 0.000 | 0.000 | 1.633 |
| 19 | 3 | 0.000 | 0.000 | 0.000 |
| 20 | 3 | 0.000 | 0.000 | 0.000 |
| Run | Blk | A | B | C |
|---|---|---|---|---|
| 1 | 1 | -1.000 | -1.000 | -1.000 |
| 2 | 1 | 1.000 | 1.000 | -1.000 |
| 3 | 1 | 1.000 | -1.000 | 1.000 |
| 4 | 1 | -1.000 | 1.000 | 1.000 |
| 5 | 1 | 0.000 | 0.000 | 0.000 |
| 6 | 1 | 0.000 | 0.000 | 0.000 |
| 7 | 2 | 1.000 | -1.000 | -1.000 |
| 8 | 2 | -1.000 | 1.000 | -1.000 |
| 9 | 2 | -1.000 | -1.000 | 1.000 |
| 10 | 2 | 1.000 | 1.000 | 1.000 |
| 11 | 2 | 0.000 | 0.000 | 0.000 |
| 12 | 2 | 0.000 | 0.000 | 0.000 |
| 13 | 3 | -1.633 | 0.000 | 0.000 |
| 14 | 3 | 1.633 | 0.000 | 0.000 |
| 15 | 3 | 0.000 | -1.633 | 0.000 |
| 16 | 3 | 0.000 | 1.633 | 0.000 |
| 17 | 3 | 0.000 | 0.000 | -1.633 |
| 18 | 3 | 0.000 | 0.000 | 1.633 |
| 19 | 3 | 0.000 | 0.000 | 0.000 |
| 20 | 3 | 0.000 | 0.000 | 0.000 |
| Run | Blk | A | B | C |
|---|---|---|---|---|
| 1 | 1 | -1.000 | -1.000 | -1.000 |
| 2 | 1 | 1.000 | 1.000 | -1.000 |
| 3 | 1 | 1.000 | -1.000 | 1.000 |
| 4 | 1 | -1.000 | 1.000 | 1.000 |
| 5 | 1 | 0.000 | 0.000 | 0.000 |
| 6 | 1 | 0.000 | 0.000 | 0.000 |
| 7 | 2 | 1.000 | -1.000 | -1.000 |
| 8 | 2 | -1.000 | 1.000 | -1.000 |
| 9 | 2 | -1.000 | -1.000 | 1.000 |
| 10 | 2 | 1.000 | 1.000 | 1.000 |
| 11 | 2 | 0.000 | 0.000 | 0.000 |
| 12 | 2 | 0.000 | 0.000 | 0.000 |
| 13 | 3 | -1.633 | 0.000 | 0.000 |
| 14 | 3 | 1.633 | 0.000 | 0.000 |
| 15 | 3 | 0.000 | -1.633 | 0.000 |
| 16 | 3 | 0.000 | 1.633 | 0.000 |
| 17 | 3 | 0.000 | 0.000 | -1.633 |
| 18 | 3 | 0.000 | 0.000 | 1.633 |
| 19 | 3 | 0.000 | 0.000 | 0.000 |
| 20 | 3 | 0.000 | 0.000 | 0.000 |
| Run | Blk | A | B | C |
|---|---|---|---|---|
| 1 | 1 | -1.000 | -1.000 | -1.000 |
| 2 | 1 | 1.000 | 1.000 | -1.000 |
| 3 | 1 | 1.000 | -1.000 | 1.000 |
| 4 | 1 | -1.000 | 1.000 | 1.000 |
| 5 | 1 | 0.000 | 0.000 | 0.000 |
| 6 | 1 | 0.000 | 0.000 | 0.000 |
| 7 | 2 | 1.000 | -1.000 | -1.000 |
| 8 | 2 | -1.000 | 1.000 | -1.000 |
| 9 | 2 | -1.000 | -1.000 | 1.000 |
| 10 | 2 | 1.000 | 1.000 | 1.000 |
| 11 | 2 | 0.000 | 0.000 | 0.000 |
| 12 | 2 | 0.000 | 0.000 | 0.000 |
| 13 | 3 | -1.633 | 0.000 | 0.000 |
| 14 | 3 | 1.633 | 0.000 | 0.000 |
| 15 | 3 | 0.000 | -1.633 | 0.000 |
| 16 | 3 | 0.000 | 1.633 | 0.000 |
| 17 | 3 | 0.000 | 0.000 | -1.633 |
| 18 | 3 | 0.000 | 0.000 | 1.633 |
| 19 | 3 | 0.000 | 0.000 | 0.000 |
| 20 | 3 | 0.000 | 0.000 | 0.000 |
The first block is a one half fraction of the \(2^3\) plus two center points. Block 2 is the second half fraction of the factorial part with two center points. The third block consists of six star points, plus to center points. Each of the three blocks contains two center points and the first two blocks have half of the corner points each. The third block contains the star points and is of size 8.
Rollover the words 'Block 1', 'Block 2', and 'Block 3' in the graphic above. Do you see how they use center points strategically to tie the blocks together? They are represented in each block and they keep the design connected.
The corner points all have +1 or -1 for every dimension, because they're at the corners. They are either up or down, in or out, right or left. The axial points have \(+\alpha\), or \(-\alpha\) \((+1.6330\ or -1.6330)\) for A, but are 0 for factors B and C. The center points have zero on all three axes, truly the center of this region. We have designed this to cover the space in just the right way so that we can estimate a quadratic equation. Using a Central Composite Design, we can't estimate cubic terms, and we can't estimate higher order interactions. If we had utilized a \(3^k\) design, one that quickly becomes unreasonably large, then we would have been able to estimate all of the higher order interactions.
However, we would have wasted a lot of resources to do it. The CCD allows us to estimate just linear and quadratic terms and first order interactions.
Example 11.1: Polymers and Elasticity
This example is from the Box and Draper (1987) book and the data from Tables 9.2 and 9.4 are in Minitab (BD9-1.csv).
This example has three variables and they are creating a polymer, a kind of plastic that has a quality of elasticity. The measurement in this experiment is the level of elasticity. We created the design in Minitab for this experiment, however the data only has two center points:
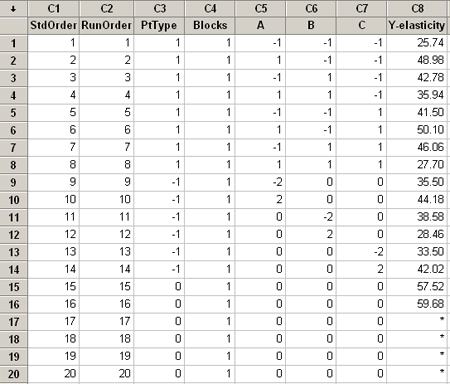
Variables A and B are the concentration of two ingredients that make up the polymer, and C is the temperature, and the response is elasticity. There are 8 corner points, a complete factorial, 6 star points and 2 center points.
Let's go right to the analysis stage now using Minitab ...
or you can view the condensed version with no audio...
Before we move on I would like to go back and take a look again at the plot of the residuals. Wait a minute! Is there something wrong with this residual plot?
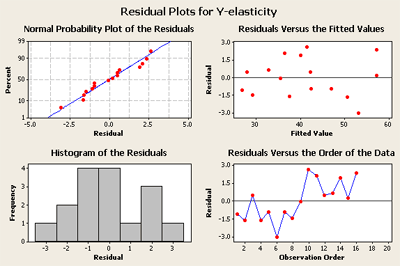
Residual plot for the polynomial fit
Look at the plot in the lower right. The first eight points tend to be low, and then the next eight points are at a higher level. This is a clue, that something is influencing the response that is not being fit by the model. This looks suspicious. What happened? My guess is that the experiment was run in two phases. They first ran the \(2^k\) part - (block 1). And then they noticed the response and added the star points to make a responsive surface design in the second part. This is often how these experiments are conducted. You first perform a first-order experiment, and then you add center points and star points and then fit the quadratic.
Add a block term and rerun the experiment to see if this makes a difference.
Two Types of Central Composite Designs
The central composite design has \(2*k\) star points on the axial lines outside of the box defined by the corner points. There are two major types of central composite designs: the spherical central composite design where the star points are the same distance from the center as the corner points, and the rotatable central composite design where the star points are shifted or placed such that the variances of the predicted values of the responses are all equal, for x’s which are an equal distance from the center.
When you are choosing, in the natural units, the values corresponding to the low and high, i.e. corresponding to -1 and 1 in coded units, keep in mind that the design will have to include points further from the center in all directions. You are trying to fit the design in the middle of your region of interest, the region where you expect the experiment to give the optimal response.
11.2.2 - Box-Behnken Designs
11.2.2 - Box-Behnken DesignsBox-Behnken Designs
Another class of response surface designs are called Box-Behnken designs. They are very useful in the same setting as the central composite designs. Their primary advantage is in addressing the issue of where the experimental boundaries should be, and in particular to avoid treatment combinations that are extreme. By extreme, we are thinking of the corner points and the star points, which are extreme points in terms of region in which we are doing our experiment. The Box-Behnken design avoids all the corner points, and the star points.
One way to think about this is that in the central composite design we have a ball where all of the corner points lie on the surface of the ball. In the Box-Behnken design the ball is now located inside the box defined by a 'wire frame' that is composed of the edges of the box. If you blew up a balloon inside this wire frame box so that it just barely extends beyond the sides of the box, it might look like this, in three dimensions. Notice where the balloon first touches the wire frame; this is where the points are selected to create the design.
Box-Behnken Design
| Factors: | 3 | Replicates: | 1 |
| Base runs: | 15 | Total runs: | 15 |
| Base Blocks: | 1 | Total Blocks: | 1 |
| Center points: | 3 | ||
Design Table
| Run | Blk | A | B | C |
|---|---|---|---|---|
| 1 | 1 | - | - | 0 |
| 2 | 1 | + | - | 0 |
| 3 | 1 | - | + | 0 |
| 4 | 1 | + | + | 0 |
| 5 | 1 | - | 0 | - |
| 6 | 1 | + | 0 | - |
| 7 | 1 | - | 0 | + |
| 8 | 1 | + | 0 | + |
| 9 | 1 | 0 | - | - |
| 10 | 1 | 0 | + | - |
| 11 | 1 | 0 | - | + |
| 12 | 1 | 0 | + | + |
| 13 | 1 | 0 | 0 | 0 |
| 14 | 1 | 0 | 0 | 0 |
| 15 | 1 | 0 | 0 | 0 |
Therefore the points are still on the surface of a ball, but the points are never further out than the low and high in any direction. In addition, there would be multiple center points as before. In this type of design, you do not need as many center points because points on the outside are closer to the middle. The number of center points are again chosen so that the variance of is about the same in the middle of the design as it is on the outside of the design.
In Minitab, we can see the different designs that are available. Listed at the bottom are the Box-Behnken Designs.
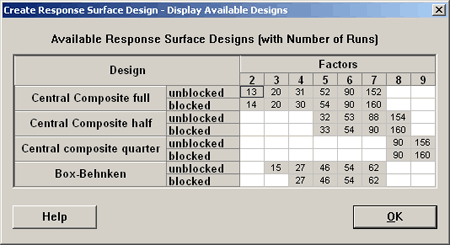
A Box-Behnken (BB) design with two factors does not exist. With three factors the BB design by default will have three center points and is given in the Minitab output shown above. The last three observations are the center points. The other points, you will notice, all include one 0 for one of the factors and then a plus or minus combination for the other two factors.
If you consider the BB design with four factors, you get the same pattern where we have two of the factors at + or - 1 and the other two factors are 0. Again, this design has three center points and a total of 27 observations.
Comparing the central composite design with 4 factors, which has 31 observations, a Box-Behnken design only includes 27 observations. For 5 factors, the Box-Behnken would have 46 observations, and a central composite would have 52 observations if you used a complete factorial, but this is where the central composite also allows you to use a fractional factorial as a means of making this experiment more efficient. Likewise, for six factors, the Box-Behnken requires 54 observations, and this is the minimum of the central composite design.
Both the CCD and the BB design can work, but they have different structures, so if your experimental region is such that extreme points are a problem then there are some advantages to the Box-Behnken. Otherwise, they both work well.
The central composite design is one that I favor because even though you are interested in the middle of a region if you put all your points in the middle you do not have as much leverage about where the model fits. So when you can move your points out you get better information about the function within your region of experimentation.
However, by moving your points too far out, you get into boundaries or could get into extreme conditions, and then enter the practical issues which might outweigh the statistical issues. The central composite design is used more often but the Box-Behnken is a good design in the sense that you can fit the quadratic model. It would be interesting to look at the variance of the predicted values for both of these designs. (This would be an interesting research question for somebody!) The question would be which of the two designs gives you a smaller average variance over the region of experimentation.
The usual justification for going to the Box-Behnken is to avoid the situation where the corner points in the central composite design are very extreme, i.e. they are at the highest level of several factors. So, because they are very extreme, the researchers may say these points are not very typical. In this case, the Box Behnken may look a lot more desirable since there are more points in the middle of the range and they are not as extreme. The Box-Behnken might feel a little 'safer' since the points are not as extreme as all of the factors.
The Variance of the Predicted Values
Let's look at this a little bit. We can write out the model:
\(\hat{y}_{x} = b_0 + b_{1}x_{1} + b_{2}x_{2} + b_{11}x_{1}^{2} + b_{22}x_{2}^{2} + b_{12}x_{1}x_{2}\)
Where the b0, b1, etc are the estimated parameters. This is a quadratic model with two x's. The question we want to answer is how many center points should there be so that the variance of the predicted value, var(\(\hat{y}_{x}\)) when x is at the center is the same as when x is at the outside of the region?
See handout Chapter 11: Supplemental Text Material. This shows the impact on the variance of predicted value in the situation with k = 2, full factorial and the design has only 2 center points rather than the 5 or 6 that the central composite design would recommend.
What you see (S11-3) is that in the middle of the region the variance is much higher than further out. So, by putting more points in the center of the design, collecting more information there, (replicating a design in the middle), you see that the standard error is lower in the middle and roughly the same as farther out. It gets larger again in the corners and continues growing as you go out from the center. By putting in enough center points you balance the variance in the middle of the region relative to further out.
Another example (S11-4) is a central composite design where the star points are on the face. It is not rotatable design and the variance changes depending on which direction you're moving out from center of the design.
It also shows another example (S11-4), also a face-centered design with zero center points, which shows a slight hump in the middle on the variance function.
Notice that we only need two center points for the face-centered design. Rather than having our star points farther out, if we move them closer into the face we do not need as many center points because we already have points closer to the center. A lot of factors affect the efficiencies of these designs.
Rotatability
Rotatability is determined by our choice of alpha. A design is rotatable if the prediction variance depends only on the distance of the design point from the center of the design. This is what we were observing previously. Here in the supplemental material (S11-5) is an example with a rotatable design, but the variance contours are based on a reduced model. It only has one quadratic term rather than two. As a result we get a slightly different shape, the point being that rotatability and equal variance contours depend both on the design and on the model that we are fitting. We are usually thinking about the full quadratic model when we make that claim.
11.3 - Mixture Experiments
11.3 - Mixture ExperimentsExample 11-2
This is another class of response surface designs where the components are not just levels of factors but a special set where the \(x_1, x_2, \dots\) are coded and are the components of the mixture such that the sum of the \(x_i = 1\). So, these make up the proportions of the mixture.
Examples
If you are making any kind of product it usually involves mixtures of ingredients. A classic example is gasoline which is a mixture of various petrochemicals. In polymer production, polymers are actually mixtures of components as well. My favorite classroom example is baking a cake. A cake is a mixture of flour, sugar, eggs, and other ingredients depending on the type of cake. It is a mixture where the levels of x are the proportions of the ingredients.
This constraint that the sum of the x's sum to 1, i.e.,
\(0 ≤ x_i ≤ 1\)
has an impact on how we analyze these experiments.
Here we will write out our usual linear model:
\(Y_i=\beta_0 + \beta_1x_{i1}+\beta_2x_{i2}+\ldots +\beta_kx_{ik}+\varepsilon_i\)
where, \(1 =\sum\limits_{j=1}^k x_{ij}\)
If you want to incorporate this constraint then we can write:
\(Y_i= \beta_1x_{i1}+\beta_2x_{i2}+\ldots +\beta_kx_{ik}+\varepsilon_i\)
in other words, if we drop the \(\beta_0\), this reduces the parameter space by 1 and then we can fit a reduced model even though the x's are each constrained.
In the quadratic model:
\(Y_h=\sum\limits_{i=1}^k \beta_i x_{hi}+\mathop{\sum\sum}\limits_{i<j}\beta_{ij}x_{hi}x_{hj}+\varepsilon_h\)
This is probably the model we are most interested in and will use the most. Then we can generalize this into a cubic model which has one additional term.
A Cubic Model
\(Y_h=\sum\limits_{i=1}^k \beta_i x_{hi} +\mathop{\sum\sum}\limits_{i<j}\beta_{ij}x_{hi}x_{hj}
+\mathop{\sum\limits^k\sum\limits^k\sum\limits^k}\limits_{i<j<l}\beta_{ijl}x_{hi}x_{hj}x_{hl}
+\varepsilon_h\)
These models are used to fit response surfaces.
Let's look at the parameter of space. Let's say that k = 2. The mixture is entirely made up of two ingredients, \(x_1\) and \(x_2\). The sum of both ingredients is a line plotted in the parameter space below: An experiment made up of two components is either all of \(x_1\) or all of \(x_2\) or something in between, a proportion of the two. Use your mouse to click and drag the intersection point along the line that serves as a boundary to this region of experimentation.
Let's take a Look at the parameter space in three dimensions. Here we have three components: \(x_1, x_2 \text{ and } x_3\). As we satisfy our constraint that the sum of all the components equal 1 and then our parameter space is the plane that cuts the three-dimensional surface, intersecting these three points in the graph below scratch that in the plot below.
Plot showing the plane where the sum: x1+x2+x3 = 1
The triangle represents the full extent of the region of experimentation in this case with the points sometimes referred to as the Barycentric coordinates. The design question we want to address is where do we do our experiment? We are not interested in any one of the corners of the triangle where only one ingredient is represented, we are interested in some way on the middle where there is a proportion of all three of the ingredients included. We will restrict it to a feasible region of experimentation somewhere in the middle area.
Let's look at an example, for instance, producing cattle feed. The ingredients might include the following: corn, oats, hay, soybean, grass, ... all sorts of things.
In some situations it might work where you might have 100% of one component, but many instances of mixtures we try to partition off a part of the space in the middle where we think the combination is optimal.
In k = 4 the region of experimentation can be represented by the shape of a tetrahedron where each of the four sides of the tetrahedron is an equalateral triangle and has its own set of Barycentric coordinates. Each face of the tetrahedron corresponds to design region where one coordinate is zero, and the remaining three must sum to 1.
11.3.1 - Two Major Types of Mixture Designs
11.3.1 - Two Major Types of Mixture DesignsSimplex Lattice Design
A {p,m} simplex lattice design for p factors (components) is defined as all possible combination of factor levels defined as
\(x_i=0,\frac{1}{m},\frac{2}{m},\cdots,1 \qquad i=1,2,\ldots,p\)
As an example, the simplex lattice design factor levels for the case of {3,2} will be
\(x_i=0,\frac{1}{2},1 \qquad i=1,2,3\)
Which results in the following design points:
\((x_1,x_2,x_3)=\{(1,0,0),(0,1,0),(0,0,1),(\frac{1}{2},\frac{1}{2},0),(\frac{1}{2},0,\frac{1}{2}),(0,\frac{1}{2},\frac{1}{2})\}\)
Simplex Centroid Design
This design which has \(2^{p}-1\) design points consist of p permutations of (1,0,0,…,0), permutations of \((1,0,0,\ldots,0),\displaystyle{p\choose 2}\), permutations of \((\dfrac{1}{2},\dfrac{1}{2},0,\ldots,0),\displaystyle{p\choose 3}\), and the overall centroid \(\displaystyle(\dfrac{1}{p},\dfrac{1}{p},\cdots,\dfrac{1}{p})\). Some simplex centroid designs for the case of p = 3 and p = 4 can be find in Figure 11.41.
Minitab handles mixture experiments which can be accessed through Stat > DOE > Mixture. It allows for building and analysis of Simplex Lattice and Simplex Centroid designs. Furthermore, it covers a third design which is named, Extreme Vertex Design. Application of Extreme Vertex designs are for cases where we have upper and lower constraints on some or all of the components making the design space smaller than the original region.
11.3.2 - Mixture Designs in Minitab
11.3.2 - Mixture Designs in MinitabHow does Minitab handle these types of experiments?
Mixture designs are a special case of response surface designs. Under the stat menu in many tab, select design of experiments, then mixture, create mixture design. Minitab then presents you with the following dialog box:
Simplex lattice option will look at the points that are extremes. Simplex lattice creates a design for p components of degree m. In this case, we want points that are made up of 0, \(1/m, 2/m, \dots\) up to 1. Classifying the points in this way tells us how we will space the points. For instance, if m = 2, then the only points we would have would be 0, 1/2, and 1 to play with in all key dimensions. You can create this design in Minitab, for 3 factors, using tab Stat > DOE > Mixture > Create Mixture Design and select Simplex Centroid. See the image here:
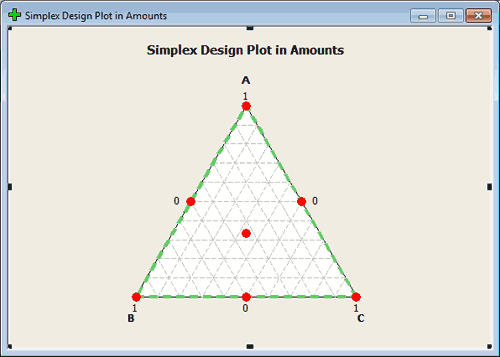
If we are in a design with the m = 3, then we would have 0, 1/3, 2/3, and 1. In this case we would have points a third of the way along each dimension. Any point on the boundary can be constructed in this way.
All of these points are on the boundary which means that they are made up of mixtures that omit one of the components. (This is not always desirable but in some settings it is fine.)
The centroid is the point in the middle. Axial points are points that lie along the lines that intersect the region of experimentation, points that are located interior and therefore include part of all of the components.
You can create this design in Minitab, for 3 factors, using tab Stat > DOE > Mixture > Create Mixture Design and select Simplex Centroid. See the image here:
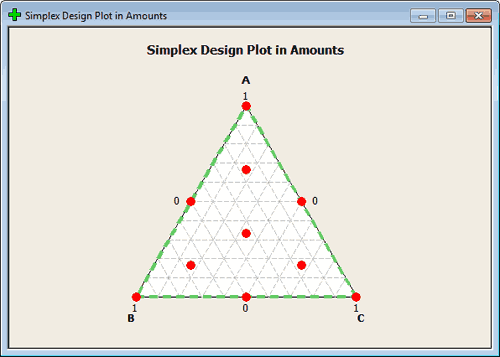
This should give you the range of points that you think of when designing in a mixture. again, you want points in the middle but like regression in an unconstrained space you typically want to have your points farther out so you have good leverage. From this perspective, the points on the outside make a lot of sense. From an actual experimentation situation, you would have to be in a scientific setting also where those points make sense. If not, we would constrain this region to begin with. We will get in to this later.
How Rich of a Design?
Let's look at the set of possible designs that Minitab gives us.
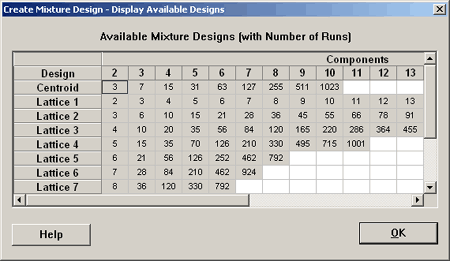
Where it is labeled on the left Lattice 1, Lattice 2, etc., here minitab is referring to degree 1, 2, etc. So, if you want a lattice of degree 1, this is not very interesting. This means that you just have a 0 and 1. If you go to a lattice of degree 2 then you need six points in three dimensions. This is pretty much what we looked at previously... (roll over the red mixture points, below).
| Run | Type | A | B | C |
|---|---|---|---|---|
| 1 | 1 | 1.0000 | 0.0000 | 0.0000 |
| 2 | 2 | 0.5000 | 0.5000 | 0.0000 |
| 3 | 2 | 0.5000 | 0.0000 | 0.5000 |
| 4 | 1 | 0.0000 | 1.0000 | 0.0000 |
| 5 | 2 | 0.0000 | 0.5000 | 0.5000 |
| 6 | 1 | 0.0000 | 0.0000 | 1.0000 |
Here is a design table for a lattice with degree 3:
| Run | Type | A | B | C |
|---|---|---|---|---|
| 1 | 1 | 1.0000 | 0.0000 | 0.0000 |
| 2 | 2 | 0.6667 | 0.3333 | 0.0000 |
| 3 | 2 | 0.6667 | 0.0000 | 0.3333 |
| 4 | 2 | 0.3333 | 0.6667 | 0.0000 |
| 5 | 0 | 0.3333 | 0.3333 | 0.3333 |
| 6 | 2 | 0.3333 | 0.0000 | 0.6667 |
| 7 | 1 | 0.0000 | 1.0000 | 0.0000 |
| 8 | 2 | 0.0000 | 0.6667 | 0.3333 |
| 9 | 2 | 0.0000 | 0.3333 | 0.6667 |
| 10 | 1 | 0.0000 | 0.0000 | 1.0000 |
Now let's go into Minitab and augment this design by including axial points. Here is what results:
| Run | Type | A | B | C |
|---|---|---|---|---|
| 1 | 1 | 1.0000 | 0.0000 | 0.0000 |
| 2 | 2 | 0.6667 | 0.3333 | 0.0000 |
| 3 | 2 | 0.6667 | 0.0000 | 0.3333 |
| 4 | 2 | 0.3333 | 0.6667 | 0.0000 |
| 5 | 0 | 0.3333 | 0.3333 | 0.3333 |
| 6 | 2 | 0.3333 | 0.0000 | 0.6667 |
| 7 | 1 | 0.0000 | 1.0000 | 0.0000 |
| 8 | 2 | 0.0000 | 0.6667 | 0.3333 |
| 9 | 2 | 0.0000 | 0.3333 | 0.6667 |
| 10 | 1 | 0.0000 | 0.0000 | 1.0000 |
| 11 | -1 | 0.6667 | 0.1667 | 0.6667 |
| 12 | -1 | 0.1667 | 0.6667 | 0.1667 |
| 13 | -1 | 0.1667 | 0.1667 | 0.6667 |
This gives us three more points. Each of these points is 2/3, 1/6, 1/6. These are interior points.
These are good designs if you can run your experiment in the whole region.
Let's take a look at four dimensions and see what the program will do here. Here is a design with four components, four dimensions, and a lattice of degree three. We have also selected to augment this design with axial and center points.
| Run | Type | A | B | C | D |
|---|---|---|---|---|---|
| 1 | 1 | 1.0000 | 0.0000 | 0.0000 | 0.0000 |
| 2 | 2 | 0.6667 | 0.3333 | 0.0000 | 0.0000 |
| 3 | 2 | 0.6667 | 0.0000 | 0.3333 | 0.0000 |
| 4 | 2 | 0.6667 | 0.0000 | 0.0000 | 0.3333 |
| 5 | 2 | 0.3333 | 0.6667 | 0.0000 | 0.0000 |
| 6 | 3 | 0.3333 | 0.3333 | 0.3333 | 0.0000 |
| 7 | 3 | 0.3333 | 0.3333 | 0.0000 | 0.3333 |
| 8 | 2 | 0.3333 | 0.0000 | 0.6667 | 0.0000 |
| 9 | 3 | 0.3333 | 0.0000 | 0.3333 | 0.3333 |
| 10 | 2 | 0.3333 | 0.0000 | 0.0000 | 0.6667 |
| 11 | 1 | 0.0000 | 1.0000 | 0.0000 | 0.0000 |
| 12 | 2 | 0.0000 | 0.6667 | 0.3333 | 0.0000 |
| 13 | 2 | 0.0000 | 0.6667 | 0.0000 | 0.3333 |
| 14 | 2 | 0.0000 | 0.3333 | 0.6667 | 0.0000 |
| 15 | 3 | 0.0000 | 0.3333 | 0.3333 | 0.3333 |
| 16 | 2 | 0.0000 | 0.3333 | 0.0000 | 0.6667 |
| 17 | 1 | 0.0000 | 0.0000 | 1.0000 | 0.0000 |
| 18 | 2 | 0.0000 | 0.0000 | 0.6667 | 0.3333 |
| 19 | 2 | 0.0000 | 0.0000 | 0.3333 | 0.6667 |
| 20 | 1 | 0.0000 | 0.0000 | 0.0000 | 1.0000 |
| 21 | 0 | 0.2500 | 0.2500 | 0.2500 | 0.2500 |
| 22 | -1 | 0.6250 | 0.1250 | 0.1250 | 0.1250 |
| 23 | -1 | 0.1250 | 0.6250 | 0.1250 | 0.1250 |
| 24 | -1 | 0.1250 | 0.1250 | 0.6250 | 0.1250 |
| 25 | -1 | 0.1250 | 0.1250 | 0.1250 | 0.6250 |
This gives us 25 points in the design and the plot shows us the four faces of the tetrahedron. It doesn't look like it is showing us a plot of the interior points.
11.3.3 - The Analysis of Mixture Designs
11.3.3 - The Analysis of Mixture DesignsExample 11.3: Elongation of Yarn
Download: Ex11-3.mwx | Ex11-3.csv
This example has to do with the elongation of yarn based on its component fabrics. There are three components in this mixture and each component is a synthetic material. The mixture design was one that we had looked at previously. It is a simple lattice design of degree 2. This means that it has mixtures of 0, 1/2, 100%. The components of this design are made up of these three possibilities.
| StdOrder | RunOrder | PtType | Blocks | A | B | C | Y | |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1.0 | 0.0 | 0.0 | 11.0 |
| 2 | 2 | 2 | 2 | 1 | 0.5 | 0.5 | 0.0 | 15.0 |
| 3 | 3 | 3 | 2 | 1 | 0.5 | 0.0 | 0.5 | 17.7 |
| 4 | 4 | 4 | 1 | 1 | 0.0 | 1.0 | 0.0 | 8.8 |
| 5 | 5 | 5 | 2 | 1 | 0.0 | 0.5 | 0.5 | 10.0 |
| 6 | 6 | 6 | 1 | 1 | 0.0 | 0.0 | 1.0 | 16.8 |
| 7 | 7 | 7 | 1 | 1 | 1.0 | 0.0 | 0.0 | 12.4 |
| 8 | 8 | 8 | 2 | 1 | 0.5 | 0.5 | 0.0 | 14.8 |
| 9 | 9 | 9 | 2 | 1 | 0.5 | 0.0 | 0.5 | 16.4 |
| 10 | 10 | 10 | 1 | 1 | 0.0 | 1.0 | 0.0 | 10.0 |
| 11 | 11 | 11 | 2 | 1 | 0.0 | 0.5 | 0.5 | 9.7 |
| 12 | 12 | 12 | 1 | 1 | 0.0 | 0.0 | 1.0 | 16.0 |
| 13 | 13 | 13 | 1 | 1 | 1.0 | 0.0 | 0.0 | * |
| 14 | 14 | 14 | 2 | 1 | 0.5 | 0.5 | 0.0 | 16.1 |
| 15 | 15 | 15 | 2 | 1 | 0.5 | 0.0 | 0.5 | 16.6 |
| 16 | 16 | 16 | 1 | 1 | 0.0 | 1.0 | 0.0 | * |
| 17 | 17 | 17 | 2 | 1 | 0.0 | 0.5 | 0.5 | 11.8 |
| 18 | 18 | 18 | 1 | 1 | 0.0 | 0.0 | 1.0 | * |
In the Minitab program, the first 6 runs show you the pure components, and in addition, you have the 5 mixed components. All of this was replicated 3 times so that we have 15 runs. There were three that had missing data.
You can also specify in more detail which type of points that you want to include in the mixture design using the dialog boxes in Minitab if your experiment requires this.
Analysis
In the analysis we fit the quadratic model ( the linear + the interaction terms). Remember we only have 6 points in this design, the vertex, the half-lengths, so we are fitting a response surface to these 6 points. Let's take a look at the analysis:
Regression for Mixtures: Y versus A, B, C
Estimated Regression Coefficients for Y (component proportions)
| Term | Coef | SE Coef | T | P | VIF |
|---|---|---|---|---|---|
| A | 11.70 | 0.6037 | * | * | 1.750 |
| B | 9.400 | 0.6037 | * | * | 1.750 |
| C | 16.400 | 0.637 | * | * | 1.750 |
| A*B | 19.000 | 2.6082 | 7.28 | 0.000 | 1.750 |
| A*C | 11.400 | 2.6082 | 4.37 | 0.002 | 1.750 |
| B*C | -9.600 | 2.6082 | -3.68 | 0.005 | 1.750 |
| S = 0.853750 | PRESS = 18.295 | |
| R-Sq = 95.14% | R- Sq(pred) = 86.43% | R-Sq(adj) = 92.43% |
Analysis of variance for Y (component proportions)
| Source | DF | Seq SS | Adj SS | Adj MS | F | P |
|---|---|---|---|---|---|---|
| Regression | 5 | 128.296 | 128.2960 | 25.6592 | 35.20 | 0.000 |
| Linear | 2 | 57.629 | 50.9200 | 25.4600 | 34.93 | 0.000 |
| Quadratic | 3 | 70.667 | 70.669 | 23.5556 | 32.32 | 0.000 |
| Residual Error | 9 | 6.560 | 6.5600 | 0.7289 | ||
| Total | 14 | 134.856 |
Here we get 2 df linear, 3 df quaratic, these are the five regression parameters. If you look at the individual coefficients, six of them because they are is no intercept, three linear and three cross-product terms... The 9 df for error are from the triple replicates and the double replicates. This is pure error and there is no additional df for lack of fit in this full model.
If we look at the coutour service plot we get:
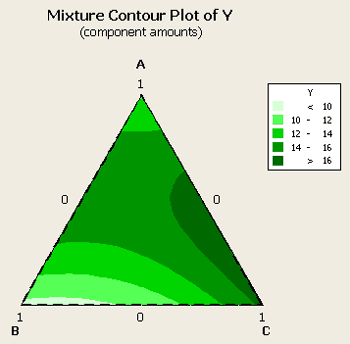
We have the optimum somewhere between a mixture of A and C, with B essentially not contributing very much at all. So, roughly 2/3rds C and 1/3 A is what we would like in our mixture. Let's look at the optimizer to find the optimum values.
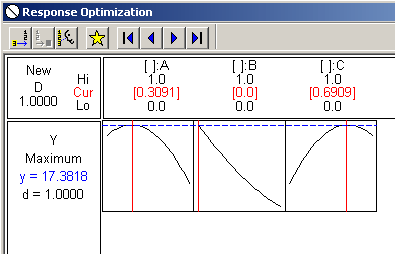
It looks like A = about .3 and B = about .7, with B not contributing nothing to the mixture.
Unless I see the plot how can I use the analysis output? How else can I determine the appropriate levels?
Example 11.4: Gasoline Production
Pr11-31.MTW from text
This example focuses on the production of an efficient gasoline mixture. The response variable is miles per gallon (mpg) as a function of the 3 components in the mixture. The data set contains these 14 points - which has duplicates at the centroid, labeled (1/3, 1/3, 1/3), and the three vertices, labeled (1,0,0), (0,1,0), and (0,0,1).
| StdOrder | RunOrder | PtType | Blocks | A | B | C | Y-mpg | |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1.00000 | 0.00000 | 0.00000 | 24.5 |
| 2 | 2 | 2 | 2 | 1 | 0.50000 | 0.50000 | 0.00000 | 25.1 |
| 3 | 3 | 3 | 2 | 1 | 0.50000 | 0.00000 | 0.50000 | 24.3 |
| 4 | 4 | 4 | 1 | 1 | 0.00000 | 1.00000 | 0.00000 | 24.8 |
| 5 | 5 | 5 | 2 | 1 | 0.00000 | 0.50000 | 0.50000 | 23.5 |
| 6 | 6 | 6 | 1 | 1 | 0.00000 | 0.00000 | 1.00000 | 22.7 |
| 7 | 7 | 7 | 0 | 1 | 0.33333 | 0.33333 | 0.33333 | 24.8 |
| 8 | 8 | 8 | -1 | 1 | 0.66667 | 0.16667 | 0.16667 | 24.2 |
| 9 | 9 | 9 | -1 | 1 | 0.16667 | 0.66667 | 0.16667 | 23.7 |
| 10 | 10 | 10 | -1 | 1 | 0.16667 | 0.16667 | 0.66667 | 23.7 |
| 11 | 11 | 11 | 1 | 1 | 1.00000 | 0.00000 | 0.00000 | 25.1 |
| 12 | 12 | 12 | 1 | 1 | 0.00000 | 1.00000 | 0.00000 | 23.9 |
| 13 | 13 | 13 | 1 | 1 | 0.00000 | 0.00000 | 1.00000 | 23.6 |
| 14 | 14 | 14 | 0 | 1 | 0.33333 | 0.33333 | 0.33333 | 24.1 |
This is a degree 2 design that has points at the vertices, middle of the edges, the center, and axial points, which are interior points, (2/3, 1/6, 1/6), (1/6, 2/3, 1/6) and (1/6, 1/6, 2/3). Also the design includes replication at the vertices and the centroid.
If you analyze this dataset without having first generated the design in Minitab, you need to tell Minitab some things about the data since you're importing it.
Analysis of variance for Y-mpg (component proportions)
| Source | DF | Seq SS | Adj SS | Adj MS | F | P |
|---|---|---|---|---|---|---|
| Regression | 5 | 4.2224 | 4.2224 | 0.84449 | 3.90 | 0.043 |
| Linear | 2 | 3.9247 | 2.7487 | 1.37433 | 6.35 | 0.022 |
| Quadratic | 3 | 0.2978 | 0.2978 | 0.09925 | 0.46 | 0.719 |
| Residual Error | 8 | 1.7319 | 1.7319 | 0.21648 | ||
| Lack-of-Fit | 4 | 0.4969 | 0.4969 | 0.12421 | 0.40 | 0.800 |
| Pure Error | 4 | 1.2350 | 1.2350 | 0.30875 | ||
| Total | 13 | 5.9543 |
The model shows a linear term significant, the quadratic terms not significant, and the lack of fit, ( a total of 10 points and we are fitting a model sex parameters - 4 df), it shows that there is no lack of fit from the model. It is not likely that it would make any difference.
If we look at the contour plot for this data:
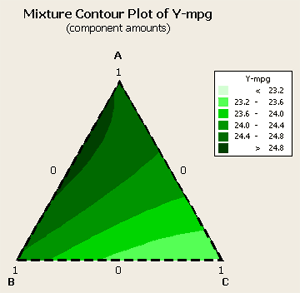
We can see that the optimum looks to be about 1/3, 2/3 between components A and B. Component C does not play hardly any role at all. Next, let's look at the optimizer for this data where we want to maximize a target of about 24.9.
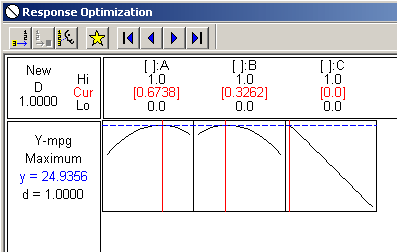
And, again, we can see that component A at the optimal level is about 2/3rds and component B is at about 1/3rd. Component C plays no part, as a matter of fact if we were to add it to the gasoline mixture it would probably lower our miles per gallon average.
Let's go back to the model and take out the factors related to component C and see what happens. When this occurs we get the following contour plot...
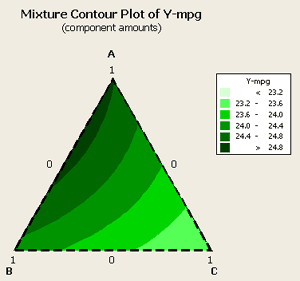
... and the following analysis:
Analysis of variance for Y-mpg (component proportions)
| Source | DF | Seq SS | Adj SS | Adj MS | F | P |
|---|---|---|---|---|---|---|
| Regression | 3 | 4.0812 | 4.0812 | 1.3604 | 7.26 | 0.007 |
| Linear | 2 | 3.9247 | 3.1548 | 1.5774 | 8.42 | 0.007 |
| Quadratic | 1 | 0.1566 | 0.1566 | 0.1566 | 0.84 | 0.382 |
| Residual Error | 10 | 18731 | 18731 | 0.1873 | ||
| Lack-of-Fit | 6 | 0.6381 | 0.6381 | 0.1063 | 0.34 | 0.882 |
| Pure Error | 4 | 1.2350 | 1.2350 | 0.3088 | ||
| Total | 13 | 5.9543 |
Our linear terms are still significant, our lack of fit is still not significant. the analysis is saying that linear is adequate for this situation and this set of data.
One says 1 ingredient and the other says a blend - which one should we use?
I would like look at the variance. ...
24.9 is the predicted value.
By having a smaller, more parimonious model you decrease the variance. This is what you would expect with a model with fewer parameters. The standard error of the fit is a function of the design, and for this reason, the fewer the parameters the smaller the variance. But is also a function of residual error which gets smaller as we throw out terms that were not significant.
11.4 - Experiments with Computer Models
11.4 - Experiments with Computer ModelsIn many cases, performing actual experiments can be much too costly and cumbersome. Instead, there might be a computer simulation of the system available which could be used as a means to generate the response values at each design point -- as an proxy for the real system output. Generally, there are two types of simulation models: Deterministic and Stochastic. Deterministic simulation models are usually complex mathematical models which provide deterministic outputs and not a random variable. The output from a stochastic simulation model is a random variable. Normally, and for optimization purposes, a program of the simulation model is built (which is called Metamodel) and based on the assumption that the simulation model is a true representation of reality, the achieved optimum condition should be in compliance with the real system. Research into optimal designs for complex models and optimal interpolation of the model output have become hot areas of research in recent years. However, in this course we will not cover any details about “experiments with computer models." More information can be found in the text and of course the relative references.