The Fitted Proportinal Odds Model

Let's fit the model and in the model we will include a test to see whether the model is valid or not.

Here we have fitted the model and have gotten the Likelihood Ratio provided towards the bottom of the output:

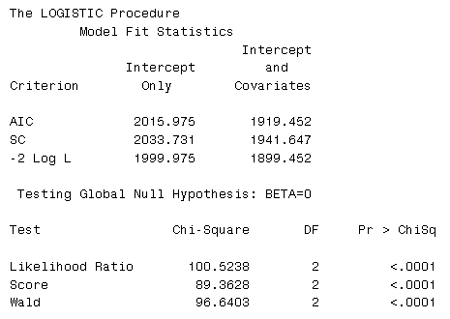
What does this likelihood ration tell us? It tells us that the coefficients U and U² are not both = 0. There is obviously an effect here...

Now we see that the model has 8 intercepts...

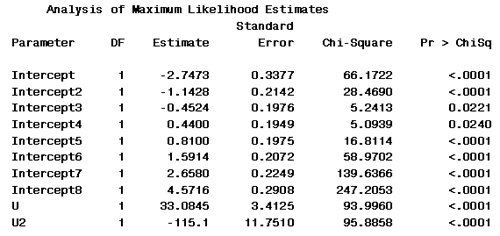
... and a coefficient for U and U². U the coefficient for the fat level is 33 and the estimated coefficient for the fat level squared is -115.

With these values in hand we need to look back at the theoretical model we are fitting. Here is the theoretical model.

Proportional Odds Model:

\(Ln Prob(Y \le i) / [1 - Prob(Y \le i)]= \alpha_i + \beta_1U + \beta_2U^2 \)

Which we will fit for our coefficients U and U² as shown below and then ...

Ln Model:

\(Ln Prob(Y \le i | U, U^2) / [1 - Prob(Y \le i | U, U^2)]= \alpha_i + \beta_1U + \beta_2U^2 \)

Fitted Model:

\(Ln Prob(Y \le i | U, U^2) / [1 - Prob(Y \le i | U, U^2)]= \hat{\alpha}_i + 33.08450 - 115.1U^2 \)

Which we can then differentiate and maximize to arrive at a final value of ...

\(\frac{dY}{dU}= 33.0845 - 230.2U^2 = 0 \rightarrow \hat{U} = 33.0845 / 230.2 = 0.14372\)

Reflecting on Polytomous Response

At what point or what number of values on your Likert scale would you hestiate to use regression and feel as though you would have to use polytomous logistic regression?

How about other Likert values that are used? Will the same principle be involved?