4.6 - Geometry of the Multivariate Normal Distribution
4.6 - Geometry of the Multivariate Normal DistributionThe geometry of the multivariate normal distribution can be investigated by considering the orientation, and shape of the prediction ellipse as depicted in the following diagram:
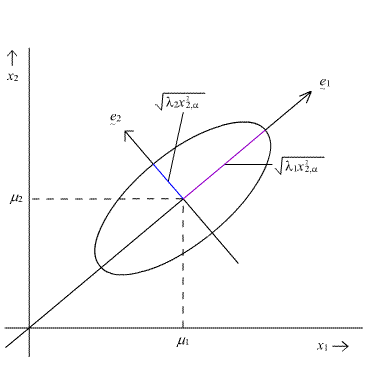
The \((1 - α) \times 100%\) prediction ellipse above is centered on the population means \(\mu_{1}\) and \(\mu_{2}\).
The ellipse has axes pointing in the directions of the eigenvectors \(e _ { 1 } , e _ { 2 } , \dots , e _ { p } \). Here, in this diagram for the bivariate normal, the longest axis of the ellipse points in the direction of the first eigenvector \(e_{1}\) and the shorter axis is perpendicular to the first, pointing in the direction of the second eigenvector \(e_{2}\).
The corresponding half-lengths of the axes are obtained by the following expression:
\(l_j = \sqrt{\lambda_j\chi^2_{p,\alpha}}\)
The plot above captures the lengths of these axes within the ellipse.
The volume (area) of the hyper-ellipse is equal to:
\(\dfrac{2\pi^{p/2}}{p\Gamma\left(\frac{p}{2}\right)}(\chi^2_{p,\alpha})^{p/2}|\Sigma|^{1/2}\)
In this expression for the volume (area) of the hyper-ellipse, \(Γ(x)\) is the gamma function. To compute the gamma function, consider the two special cases:
Case I: p is even
\(\Gamma\left(\frac{p}{2}\right) = \left(\frac{p}{2}-1\right)!\)
Case II: p is odd
\(\Gamma\left(\frac{p}{2}\right) = \dfrac{1 \times 3 \times 5 \times \dots \times (p-2) \times \sqrt{\pi}}{2^{(p-1)/2}}\)
We shall illustrate the shape of the multivariate normal distribution using the Wechsler Adult Intelligence Scale data.