Lesson 11: Principal Components Analysis (PCA)
Lesson 11: Principal Components Analysis (PCA)Overview
Sometimes data are collected on a large number of variables from a single population. As an example consider the Places Rated dataset below.
Example 11-1: Places Rated
In the Places Rated Almanac, Boyer and Savageau rated 329 communities according to the following nine criteria:
- Climate and Terrain
- Housing
- Health Care & the Environment
- Crime
- Transportation
- Education
- The Arts
- Recreation
- Economics
Objective
With a large number of variables, the dispersion matrix may be too large to study and interpret properly. There would be too many pairwise correlations between the variables to consider. Graphical displays may also not be particularly helpful when the data set is very large. With 12 variables, for example, there will be more than 200 three-dimensional scatterplots.
To interpret the data in a more meaningful form, it is necessary to reduce the number of variables to a few, interpretable linear combinations of the data. Each linear combination will correspond to a principal component.
(There is another very useful data reduction technique called Factor Analysis discussed in a subsequent lesson.)
Objectives
- Perform a principal components analysis using SAS and Minitab
- Assess how many principal components are needed;
- Interpret principal component scores and describe a subject with a high or low score;
- Determine when a principal component analysis should be based on the variance-covariance matrix or the correlation matrix;
- Compare principal component scores in further analyses.
11.1 - Principal Component Analysis (PCA) Procedure
11.1 - Principal Component Analysis (PCA) ProcedureSuppose that we have a random vector \(\mathbf{X}\).
\(\textbf{X} = \left(\begin{array}{c} X_1\\ X_2\\ \vdots \\X_p\end{array}\right)\)
with population variance-covariance matrix
\(\text{var}(\textbf{X}) = \Sigma = \left(\begin{array}{cccc}\sigma^2_1 & \sigma_{12} & \dots &\sigma_{1p}\\ \sigma_{21} & \sigma^2_2 & \dots &\sigma_{2p}\\ \vdots & \vdots & \ddots & \vdots \\ \sigma_{p1} & \sigma_{p2} & \dots & \sigma^2_p\end{array}\right)\)
Consider the linear combinations
\(\begin{array}{lll} Y_1 & = & e_{11}X_1 + e_{12}X_2 + \dots + e_{1p}X_p \\ Y_2 & = & e_{21}X_1 + e_{22}X_2 + \dots + e_{2p}X_p \\ & & \vdots \\ Y_p & = & e_{p1}X_1 + e_{p2}X_2 + \dots +e_{pp}X_p\end{array}\)
Each of these can be thought of as linear regression, predicting \(Y_{i}\) from \(X_{1}\), \(X_{2}\), ... , \(X_{p}\). There is no intercept, but \(e_{i1}\), \(e_{i2}\), ..., \(e_{ip}\) can be viewed as regression coefficients.
Note that \(Y_{i}\) is a function of our random data, and so is also random. Therefore it has a population variance
\(\text{var}(Y_i) = \sum\limits_{k=1}^{p}\sum\limits_{l=1}^{p}e_{ik}e_{il}\sigma_{kl} = \mathbf{e}'_i\Sigma\mathbf{e}_i\)
Moreover, \(Y_{i}\) and \(Y_{j}\) have population covariance
\(\text{cov}(Y_i, Y_j) = \sum\limits_{k=1}^{p}\sum\limits_{l=1}^{p}e_{ik}e_{jl}\sigma_{kl} = \mathbf{e}'_i\Sigma\mathbf{e}_j\)
Collect the coefficients \(e_{ij}\) into the vector
\(\mathbf{e}_i = \left(\begin{array}{c} e_{i1}\\ e_{i2}\\ \vdots \\ e_{ip}\end{array}\right)\)
First Principal Component (PCA1): \(\boldsymbol{Y}_{1}\)
The first principal component is the linear combination of x-variables that has maximum variance (among all linear combinations). It accounts for as much variation in the data as possible.
Specifically, we define coefficients \( \boldsymbol { e } _ { 11, } \boldsymbol { e } _ { 12 }, \ldots, \boldsymbol { e } _ { 1 p }\) for the first component in such a way that its variance is maximized, subject to the constraint that the sum of the squared coefficients is equal to one. This constraint is required so that a unique answer may be obtained.
More formally, select \(\boldsymbol { e } _ { 11 , } \boldsymbol { e } _ { 12 } , \ldots , \boldsymbol { e } _ { 1 p }\) that maximizes
\(\text{var}(Y_1) = \sum\limits_{k=1}^{p}\sum\limits_{l=1}^{p}e_{1k}e_{1l}\sigma_{kl} = \mathbf{e}'_1\Sigma\mathbf{e}_1\)
subject to the constraint that
\(\mathbf{e}'_1\mathbf{e}_1 = \sum\limits_{j=1}^{p}e^2_{1j} = 1\)
Second Principal Component (PCA2): \(\boldsymbol{Y}_{2}\)
The second principal component is the linear combination of x-variables that accounts for as much of the remaining variation as possible, with the constraint that the correlation between the first and second components is 0
Select \(\boldsymbol { e } _ { 21 , } \boldsymbol { e } _ { 22 } , \ldots , \boldsymbol { e } _ { 2 p }\) that maximizes the variance of this new component...
\(\text{var}(Y_2) = \sum\limits_{k=1}^{p}\sum\limits_{l=1}^{p}e_{2k}e_{2l}\sigma_{kl} = \mathbf{e}'_2\Sigma\mathbf{e}_2\)
subject to the constraint that the sums of squared coefficients add up to one,
\(\mathbf{e}'_2\mathbf{e}_2 = \sum\limits_{j=1}^{p}e^2_{2j} = 1\)
along with the additional constraint that these two components are uncorrelated.
\(\text{cov}(Y_1, Y_2) = \sum\limits_{k=1}^{p}\sum\limits_{l=1}^{p}e_{1k}e_{2l}\sigma_{kl} = \mathbf{e}'_1\Sigma\mathbf{e}_2 = 0\)
All subsequent principal components have this same property – they are linear combinations that account for as much of the remaining variation as possible and they are not correlated with the other principal components.
We will do this in the same way with each additional component. For instance:
\(i^{th}\) Principal Component (PCAi): \(\boldsymbol{Y}_{i}\)
We select \(\boldsymbol { e } _ { i1 , } \boldsymbol { e } _ { i2 } , \ldots , \boldsymbol { e } _ { i p }\) to maximize
\(\text{var}(Y_i) = \sum\limits_{k=1}^{p}\sum\limits_{l=1}^{p}e_{ik}e_{il}\sigma_{kl} = \mathbf{e}'_i\Sigma\mathbf{e}_i\)
subject to the constraint that the sums of squared coefficients add up to one...along with the additional constraint that this new component is uncorrelated with all the previously defined components.
\(\mathbf{e}'_i\mathbf{e}_i = \sum\limits_{j=1}^{p}e^2_{ij} = 1\)
\(\text{cov}(Y_1, Y_i) = \sum\limits_{k=1}^{p}\sum\limits_{l=1}^{p}e_{1k}e_{il}\sigma_{kl} = \mathbf{e}'_1\Sigma\mathbf{e}_i = 0\),
\(\text{cov}(Y_2, Y_i) = \sum\limits_{k=1}^{p}\sum\limits_{l=1}^{p}e_{2k}e_{il}\sigma_{kl} = \mathbf{e}'_2\Sigma\mathbf{e}_i = 0\),
\(\vdots\)
\(\text{cov}(Y_{i-1}, Y_i) = \sum\limits_{k=1}^{p}\sum\limits_{l=1}^{p}e_{i-1,k}e_{il}\sigma_{kl} = \mathbf{e}'_{i-1}\Sigma\mathbf{e}_i = 0\)
Therefore all principal components are uncorrelated from one another.
11.2 - How do we find the coefficients?
11.2 - How do we find the coefficients?How do we find the coefficients \(\boldsymbol{e_{ij}}\) for a principal component?
The solution involves the eigenvalues and eigenvectors of the variance-covariance matrix \(Σ\).
Let \(\lambda_1\) through \(\lambda_p\) denote the eigenvalues of the variance-covariance matrix \(Σ\). These are ordered so that \(\lambda_1\) has the largest eigenvalue and \(\lambda_p\) is the smallest.
\(\lambda_1 \ge \lambda_2 \ge \dots \ge \lambda_p\)
Let the vectors \(\boldsymbol{e}_1\) through \(\boldsymbol{e}_1\)
\(\boldsymbol{e}_1 , \boldsymbol{e}_2 , \dots , \boldsymbol{e}_p\)
denote the corresponding eigenvectors. It turns out that the elements for these eigenvectors are the coefficients of our principal components.
The variance for the ith principal component is equal to the ith eigenvalue.
\(var(Y_i) = \text{var}(e_{i1}X_1 + e_{i2}X_2 + \dots e_{ip}X_p) = \lambda_i\)
Moreover, the principal components are uncorrelated from one another.
\(\text{cov}(Y_i, Y_j) = 0\)
The variance-covariance matrix may be written as a function of the eigenvalues and their corresponding eigenvectors. This is determined by the Spectral Decomposition Theorem. This will become useful later when we investigate topics under factor analysis.
Spectral Decomposition Theorem
The variance-covariance matrix can be written as the sum over the p eigenvalues, multiplied by the product of the corresponding eigenvector times its transpose as shown in the first expression below:
\begin{align} \Sigma & = \sum_{i=1}^{p}\lambda_i \mathbf{e}_i \mathbf{e}_i' \\ & \cong \sum_{i=1}^{k}\lambda_i \mathbf{e}_i\mathbf{e}_i'\end{align}
The second expression is a useful approximation if \(\lambda_{k+1}, \lambda_{k+2}, \dots , \lambda_{p}\) are small. We may approximate Σ by
\(\sum\limits_{i=1}^{k}\lambda_i\mathbf{e}_i\mathbf{e}_i'\)
Again, this is more useful when we talk about factor analysis.
Earlier in the course, we defined the total variation of \(\mathbf{X}\) as the trace of the variance-covariance matrix, that is the sum of the variances of the individual variables. This is also equal to the sum of the eigenvalues as shown below:
\begin{align} trace(\Sigma) & = \sigma^2_1 + \sigma^2_2 + \dots +\sigma^2_p \\ & = \lambda_1 + \lambda_2 + \dots + \lambda_p\end{align}
This will give us an interpretation of the components in terms of the amount of the full variation explained by each component. The proportion of variation explained by the ith principal component is then defined to be the eigenvalue for that component divided by the sum of the eigenvalues. In other words, the ith principal component explains the following proportion of the total variation:
\(\dfrac{\lambda_i}{\lambda_1 + \lambda_2 + \dots + \lambda_p}\)
A related quantity is the proportion of variation explained by the first k principal component. This would be the sum of the first k eigenvalues divided by its total variation.
\(\dfrac{\lambda_1 + \lambda_2 + \dots + \lambda_k}{\lambda_1 + \lambda_2 + \dots + \lambda_p}\)
Naturally, if the proportion of variation explained by the first k principal components is large, then not much information is lost by considering only the first k principal components.
Why It May Be Possible to Reduce Dimensions
When we have a correlation (multicollinearity) between the x-variables, the data may more or less fall on a line or plane in a lower number of dimensions. For instance, imagine a plot of two x-variables that have a nearly perfect correlation. The data points will fall close to a straight line. That line could be used as a new (one-dimensional) axis to represent the variation among data points. As another example, suppose that we have verbal, math, and total SAT scores for a sample of students. We have three variables, but really (at most) two dimensions to the data because total= verbal+math, meaning the third variable is completely determined by the first two. The reason for saying “at most” two dimensions is that if there is a strong correlation between verbal and math, then it may be possible that there is only one true dimension to the data.
All of this is defined in terms of the population variance-covariance matrix Σ which is unknown. However, we may estimate Σ by the sample variance-covariance matrix given in the standard formula here:
\(\textbf{S} = \frac{1}{n-1} \sum\limits_{i=1}^{n}(\mathbf{X}_i-\bar{\textbf{x}})(\mathbf{X}_i-\bar{\textbf{x}})'\)
Procedure
Compute the eigenvalues \(\hat{\lambda}_1, \hat{\lambda}_2, \dots, \hat{\lambda}_p\) of the sample variance-covariance matrix S, and the corresponding eigenvectors \(\hat{\mathbf{e}}_1, \hat{\mathbf{e}}_2, \dots, \hat{\mathbf{e}}_p\).
Then we define the estimated principal components using the eigenvectors as the coefficients:
\begin{align} \hat{Y}_1 & = \hat{e}_{11}X_1 + \hat{e}_{12}X_2 + \dots + \hat{e}_{1p}X_p \\ \hat{Y}_2 & = \hat{e}_{21}X_1 + \hat{e}_{22}X_2 + \dots + \hat{e}_{2p}X_p \\&\vdots\\ \hat{Y}_p & = \hat{e}_{p1}X_1 + \hat{e}_{p2}X_2 + \dots + \hat{e}_{pp}X_p \\ \end{align}
Generally, we only retain the first k principal components. Here we must balance two conflicting desires:
- To obtain the simplest possible interpretation, we want k to be as small as possible. If we can explain most of the variation just by two principal components then this would give us a simple description of the data. When k is small, the first k components explain a large portion of the overall variation. If the first few components explain a small amount of variation, we need more of them to explain a desired percentage of total variance resulting in a large k.
- To avoid loss of information, we want the proportion of variation explained by the first k principal components to be large. Ideally as close to one as possible; i.e., we want
\(\dfrac{\hat{\lambda}_1 + \hat{\lambda}_2 + \dots + \hat{\lambda}_k}{\hat{\lambda}_1 + \hat{\lambda}_2 + \dots + \hat{\lambda}_p} \cong 1\)
11.3 - Example: Places Rated
11.3 - Example: Places RatedExample 11-2: Places Rated
We will use the Places Rated Almanac data (Boyer and Savageau) which rates 329 communities according to nine criteria:
- Climate and Terrain
- Housing
- Health Care & Environment
- Crime
- Transportation
- Education
- The Arts
- Recreation
- Economics
Notes
- The data for many of the variables are strongly skewed to the right.
- The log transformation was used to normalize the data.
Download the text file that contains the data here: places.csv
The SAS program will implement the principal component procedures:
Download the SAS program here: places.sas
View the video explanation of the SAS code.Note: In the upper right-hand corner of the code block you will have the option of copying ( ) the code to your clipboard or downloading ( ) the file to your computer.
options ls=78;
title "PCA - Covariance Matrix - Places Rated";
/* After reading in the places data, the (base 10) log transformations are taken.
* This is an optional step and not required for the pca analysis.
*/
data places;
infile "D:\Statistics\STAT 505\data\places.csv" firstobs=2 delimiter=',';
input climate housing health crime trans educate arts recreate econ id;
climate=log10(climate);
housing=log10(housing);
health=log10(health);
crime=log10(crime);
trans=log10(trans);
educate=log10(educate);
arts=log10(arts);
recreate=log10(recreate);
econ=log10(econ);
run;
/* The princomp procedure performs pca on the places data.
* The cov option specifies results are calculated from the covariance
* matrix, instead of the default correlation matrix.
* The out=a option saves results to a data set named 'a'.
*/
proc princomp data=places cov out=a;
var climate housing health crime trans educate arts recreate econ;
run;
/* The corr procedure is used to calculate pairwise correlations
* between the first 3 principal components and the original variables.
*/
proc corr data=a;
var prin1 prin2 prin3 climate housing health crime trans educate arts
recreate econ;
run;
/* The gplot procedure is used to plot the first 2 principal components.
* axis1 and axis2 options set the plotting window size,
* and these are then set to vertical and horizontal axes, respectively.
*/
proc gplot data=a;
axis1 length=5 in;
axis2 length=5 in;
plot prin2*prin1 / vaxis=axis1 haxis=axis2;
run;
When you examine the output, the first thing that SAS does is provide summary information. There are 329 observations representing the 329 communities in our dataset and 9 variables. This is followed by simple statistics that report the means and standard deviations for each variable.
Below this is the variance-covariance matrix for the data. You should be able to see that the variance reported for the climate is 0.01289.
What we really need to draw our attention to here is the eigenvalues of the variance-covariance matrix. In the SAS output, the eigenvalues are in ranked order from largest to smallest. These values appear in Table 1 below for discussion.
Principal components analysis (covariance matrix)
To perform principal components analysis on the covariance matrix:
- Open the ‘places’ data set in a new worksheet.
- Transform variables. This step is optional but used in the steps below.
- Calc > Calculator
- Highlight and select ‘climate’ to move it to the Store result window.
- In the Expression window, enter LOGTEN( 'climate' ) to apply the (base 10) log transformation to the climate variable.
- Choose OK. The transformed values replace the originals in the worksheet under ‘climate’.
- Repeat sub-steps 1) through 4) above for all variables housing through econ.
- Stat > Multivariate > Principal Components
- Highlight and select climate through econ to move all 9 variables to the Variables window.
- Choose 9 for number of components.
- Check Covariance for Type of Matrix.
- Under Storage, for the Coefficients and Eigenvalues, enter c11 and c12 (or any two unused columns in the worksheet).
- Choose OK and OK again. The results are displayed in the results area and stored in worksheet columns as well.
Data Analysis
Step 1: Examine the eigenvalues to determine how many principal components should be considered:
Table 1. Eigenvalues and the proportion of variation are explained by the principal components.
| Component | Eigenvalue | Proportion | Cumulative |
|---|---|---|---|
| 1 | 0.3775 | 0.7227 | 0.7227 |
| 2 | 0.0511 | 0.0977 | 0.8204 |
| 3 | 0.0279 | 0.0535 | 0.8739 |
| 4 | 0.0230 | 0.0440 | 0.9178 |
| 5 | 0.0168 | 0.0321 | 0.9500 |
| 6 | 0.0120 | 0.0229 | 0.9728 |
| 7 | 0.0085 | 0.0162 | 0.9890 |
| 8 | 0.0039 | 0.0075 | 0.9966 |
| 9 | 0.0018 | 0.0034 | 1.0000 |
| Total | 0.5225 |
If you take all of these eigenvalues and add them up, then you get a total variance of 0.5223.
The proportion of variation explained by each eigenvalue is given in the third column. For example, 0.3775 divided by 0.5223 equals 0.7227, or, about 72% of the variation is explained by this first eigenvalue. The cumulative percentage explained is obtained by adding the successive proportions of variation explained to obtain the running total. For instance, 0.7227 plus 0.0977 equals 0.8204, and so forth. Therefore, about 82% of the variation is explained by the first two eigenvalues together.
Next, we need to look at successive differences between the eigenvalues. Subtracting the second eigenvalue 0.051 from the first eigenvalue, 0.377 we get a difference of 0.326. The difference between the second and third eigenvalues is 0.0232; the next difference is 0.0049. Subsequent differences are even smaller. A sharp drop from one eigenvalue to the next may serve as another indicator of how many eigenvalues to consider.
The first three principal components explain 87% of the variation. This is an acceptably large percentage.
An Alternative Method to determine the number of principal components is to look at a Scree Plot. With the eigenvalues ordered from largest to smallest, a scree plot is the plot of \(\hat{\lambda_i}\) versus i. The number of components is determined at the point beyond which the remaining eigenvalues are all relatively small and of comparable size. The following plot is made in Minitab.
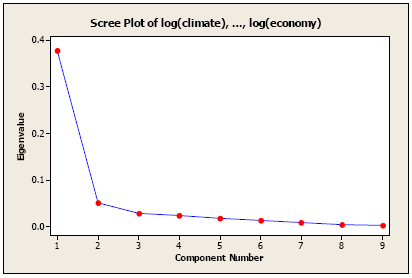
The scree plot for the variables without standardization (covariance matrix)
As you see, we could have stopped at the second principal component, but we continued till the third component. Relatively speaking, the contribution of the third component is small compared to the second component.
Step 2: Next, we compute the principal component scores. For example, the first principal component can be computed using the elements of the first eigenvector:
\begin{align}\hat{Y}_1 & = 0.0351 \times (\text{climate}) + 0.0933 \times (\text{housing}) + 0.4078 \times (\text{health})\\ & + 0.1004 \times (\text{crime}) + 0.1501 \times (\text{transportation}) + 0.0321 \times (\text{education}) \\ & 0.8743 \times (\text{arts}) + 0.1590 \times (\text{recreation}) + 0.0195 \times (\text{economy})\end{align}
In order to complete this formula and compute the principal component for the individual community of interest, plug in that community's values for each of these variables. A fairly standard procedure is to use the difference between the variables and their sample means rather than the raw data. This is known as a translation of the random variables. Translation does not affect the interpretations because the variances of the original variables are the same as those of the translated variables.
The magnitudes of the coefficients give the contributions of each variable to that component. However, the magnitude of the coefficients also depends on the variances of the corresponding variables.
11.4 - Interpretation of the Principal Components
11.4 - Interpretation of the Principal ComponentsExample 11-2: Places Rated, continued
Step 3: To interpret each component, we must compute the correlations between the original data and each principal component.
These correlations are obtained using the correlation procedure. In the variable statement, we include the first three principal components, "prin1, prin2, and prin3", in addition to all nine of the original variables. We use the correlations between the principal components and the original variables to interpret these principal components.
Because of standardization, all principal components will have a mean of 0. The standard deviation is also given for each of the components and these are the square root of the eigenvalue.
The correlations between the principal components and the original variables are copied into the following table for the Places Rated Example. You will also note that if you look at the principal components themselves, then there is zero correlation between the components.
| Principal Component | |||
|---|---|---|---|
| Variable | 1 | 2 | 3 |
| Climate | 0.190 | 0.017 | 0.207 |
| Housing | 0.544 | 0.020 | 0.204 |
| Health | 0.782 | -0.605 | 0.144 |
| Crime | 0.365 | 0.294 | 0.585 |
| Transportation | 0.585 | 0.085 | 0.234 |
| Education | 0.394 | -0.273 | 0.027 |
| Arts | 0.985 | 0.126 | -0.111 |
| Recreation | 0.520 | 0.402 | 0.519 |
| Economy | 0.142 | 0.150 | 0.239 |
Interpretation of the principal components is based on finding which variables are most strongly correlated with each component, i.e., which of these numbers are large in magnitude, the farthest from zero in either direction. Which numbers we consider to be large or small is of course a subjective decision. You need to determine at what level the correlation is of importance. Here a correlation above 0.5 is deemed important. These larger correlations are in boldface in the table above:
We will now interpret the principal component results with respect to the value that we have deemed significant.
First Principal Component Analysis - PCA1
The first principal component is strongly correlated with five of the original variables. The first principal component increases with increasing Arts, Health, Transportation, Housing, and Recreation scores. This suggests that these five criteria vary together. If one increases, then the remaining ones tend to increase as well. This component can be viewed as a measure of the quality of Arts, Health, Transportation, and Recreation, and the lack of quality in Housing (recall that high values for Housing are bad). Furthermore, we see that the first principal component correlates most strongly with the Arts. In fact, we could state that based on the correlation of 0.985 that this principal component is primarily a measure of the Arts. It would follow that communities with high values tend to have a lot of arts available, in terms of theaters, orchestras, etc. Whereas communities with small values would have very few of these types of opportunities.
Second Principal Component Analysis - PCA2
The second principal component increases with only one of the values, decreasing Health. This component can be viewed as a measure of how unhealthy the location is in terms of available health care including doctors, hospitals, etc.
Third Principal Component Analysis - PCA3
The third principal component increases with increasing Crime and Recreation. This suggests that places with high crime also tend to have better recreation facilities.
To complete the analysis we oftentimes would like to produce a scatter plot of the component scores.
In looking at the program, you will see a gplot procedure at the bottom where we plot the second component against the first component. A similar plot can also be prepared in Minitab but is not shown here.
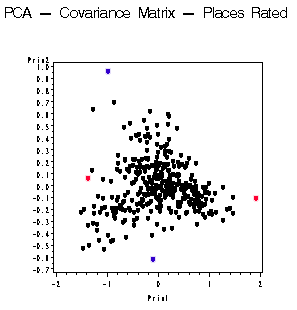
Each dot in this plot represents one community. Looking at the red dot out by itself to the right, you may conclude that this particular dot has a very high value for the first principal component and we would expect this community to have high values for the Arts, Health, Housing, Transportation, and Recreation. Whereas if you look at the red dot at the left of the spectrum, you would expect to have low values for each of those variables.
The top dot in blue has a high value for the second component. We would not expect this community to have the best Health Care. And conversely, if you were to look at the blue dot on the bottom, the corresponding community would have high values for Health Care.
Further analyses may include:
- Scatter plots of principal component scores. In the present context, we may wish to identify the locations of each point in the plot to see if places with high levels of a given component tend to be clustered in a particular region of the country, while sites with low levels of that component are clustered in another region of the country.
- Principal components are often treated as dependent variables for regression and analysis of variance.
11.5 - Alternative: Standardize the Variables
11.5 - Alternative: Standardize the VariablesIn the previous example, we looked at a principal components analysis applied to the raw data. In our earlier discussion, we noted that if the raw data is used, then a principal component analysis will tend to give more emphasis to those variables that have higher variances than to those variables that have lower variances. In effect, the results of the analysis will depend on the units of measurement used to measure each variable. That would imply that a principal component analysis should only be used with the raw data if all variables have the same units of measure. And even in this case, only if you wish to give those variables which have higher variances more weight in the analysis.
A unique example of this type of implementation might be in an ecological setting where you are looking at counts of different species of organisms at a number of different sample sites. Here, one may want to give more weight to the more common species that are observed. By analyzing the raw data you will tend to find that more common species will also show higher variances and will be given more emphasis. If you were to do a principal component analysis on standardized counts, all species would be weighted equally regardless of how abundant they are and hence, you may find some very rare species entering in as significant contributors in the analysis. This may or may not be desirable. These types of decisions need to be made with a scientist from the field.
Summary
- The results of the principal component analysis depend on the measurement scales.
- Variables with the highest sample variances tend to be emphasized in the first few principal components.
- Principal component analysis using the covariance function should only be considered if all of the variables have the same units of measurement.
If the variables have different units of measurement, (i.e., pounds, feet, gallons, etc), or if we wish each variable to receive equal weight in the analysis, then the variables should be standardized before conducting a principal components analysis. To standardize a variable, subtract the mean and divide by the standard deviation:
\(Z_{ij} = \frac{X_{ij}-\bar{x}_j}{s_j}\)
where
- \(X_{ij}\) = Data for variable j in sample unit i
- \(\bar{x}_{j}\)= Sample mean for variable j
- \(s_j\) = Sample standard deviation for variable j
Principal Component Analysis Procedure with Standardized Data
The principal components are first calculated by obtaining the eigenvalues for the correlation matrix:
\(\hat{\lambda}_1, \hat{\lambda}_2, \dots, \hat{\lambda}_p\)
In this matrix, we denote the eigenvalues of the sample correlation matrix R and the corresponding eigenvectors
\(\mathbf{\hat{e}}_1, \mathbf{\hat{e}}_2, \dots, \mathbf{\hat{e}}_p\)
The estimated principal components scores are calculated using formulas similar to before, but instead of using the raw data we use the standardized data:
\begin{align} \hat{Y}_1 & = \hat{e}_{11}Z_1 + \hat{e}_{12}Z_2 + \dots + \hat{e}_{1p}Z_p \\ \hat{Y}_2 & = \hat{e}_{21}Z_1 + \hat{e}_{22}Z_2 + \dots + \hat{e}_{2p}Z_p \\&\vdots\\ \hat{Y}_p & = \hat{e}_{p1}Z_1 + \hat{e}_{p2}Z_2 + \dots + \hat{e}_{pp}Z_p \\ \end{align}
The rest of the procedure and the interpretations follow as discussed before.
11.6 - Example: Places Rated after Standardization
11.6 - Example: Places Rated after StandardizationExample 11-3: Place Rated (after Standardization)
The SAS program implements the principal component procedures with standardized data:
download the SAS Program here: places1.sas
Note: In the upper right-hand corner of the code block you will have the option of copying ( ) the code to your clipboard or downloading ( ) the file to your computer.
options ls=78;
title "PCA - Correlation Matrix - Places Rated";
/* After reading in the places data, the (base 10) log transformations are taken.
* This is an optional step and not required for the pca analysis.
*/
data places;
infile "D:\Statistics\STAT 505\data\places.csv" firstobs=2 delimiter=',';
input climate housing health crime trans educate arts recreate econ id;
climate=log10(climate);
housing=log10(housing);
health=log10(health);
crime=log10(crime);
trans=log10(trans);
educate=log10(educate);
arts=log10(arts);
recreate=log10(recreate);
econ=log10(econ);
run;
/* The princomp procedure performs pca on the correlation matrix.
* The out=a option saves results to a data set named 'a'.
*/
proc princomp data=places out=a;
var climate housing health crime trans educate arts recreate econ;
run;
/* The corr procedure is used to calculate pairwise correlations
* between the first 3 principal components and the original variables.
*/
proc corr data=a;
var prin1 prin2 prin3 climate housing health crime trans educate arts
recreate econ;
run;
proc gplot data=a;
axis1 length=5 in;
axis2 length=5 in;
plot prin2*prin1 / vaxis=axis1 haxis=axis2;
run;
The output begins with descriptive information including the means and standard deviations for the individual variables presented.
This is followed by the Correlation Matrix for the data. For example, the correlation between the housing and climate data was only 0.273. There are no hypotheses presented that these correlations are equal to zero. We will use this correlation matrix instead to obtain our eigenvalues and eigenvectors.
Principal components analysis (correlation matrix)
To perform principal components analysis on the correlation matrix
- Open the ‘places’ data set in a new worksheet.
- Transform variables. This step is optional but used in the steps below.
- Calc > Calculator
- Highlight and select ‘climate’ to move it to the Store result window.
- In the Expression window, enter LOGTEN( 'climate') to apply the (base 10) log transformation to the climate variable.
- Choose OK. The transformed values replace the originals in the worksheet under ‘climate’.
- Repeat sub-steps 1) through 4) above for all variables housing through econ.
- Stat > Multivariate > Principal Components
- Highlight and select climate through econ to move all 9 variables to the Variables window.
- Choose 9 for number of components.
- Check Correlation for Type of Matrix.
- Under Storage, for the Coefficients and Eigenvalues, enter c11 and c12 (or any two unused columns in the worksheet).
- Choose OK and OK again. The results are displayed in the results area and stored in worksheet columns as well.
Analysis
We need to focus on the eigenvalues of the correlation matrix that correspond to each of the principal components. In this case, the total variation of the standardized variables is equal to p, the number of variables. After standardization, each variable has a variance equal to one, and the total variation is the sum of these variations, in this case, the total variation will be 9.
The eigenvalues of the correlation matrix are given in the second column in the table below. The proportion of variation explained by each of the principal components as well as the cumulative proportion of the variation explained are also provided.
Step 1
Examine the eigenvalues to determine how many principal components to consider:
| Component | Eigenvalue | Proportion | Cumulative |
|---|---|---|---|
| 1 | 3.2978 | 0.3664 | 0.3664 |
| 2 | 1.2136 | 0.1348 | 0.5013 |
| 3 | 1.1055 | 0.1228 | 0.6241 |
| 4 | 0.9073 | 0.1008 | 0.7249 |
| 5 | 0.8606 | 0.0956 | 0.8205 |
| 6 | 0.5622 | 0.0625 | 0.8830 |
| 7 | 0.4838 | 0.0538 | 0.9368 |
| 8 | 0.3181 | 0.0353 | 0.9721 |
| 9 | 0.2511 | 0.0279 | 1.0000 |
The first principal component explains about 37% of the variation. Furthermore, the first four principal components explain 72%, while the first five principal components explain 82% of the variation. Compare these proportions with those obtained using non-standardized variables. This analysis is going to require a larger number of components to explain the same amount of variation as the original analysis using the variance-covariance matrix. This is not unusual.
In most cases, the required cut-off is pre-specified; i.e. how much of the variation to be explained is pre-determined. For instance, I might state that I would be satisfied if I could explain 70% of the variation. If we do this, then we would select the components necessary until you get up to 70% of the variation. This would be one approach. This type of judgment is arbitrary and hard to make if you are not experienced with these types of analysis. The goal - to some extent - also depends on the type of problem at hand.
Another approach would be to plot the differences between the ordered values and look for a break or a sharp drop. The only sharp drop that is noticeable in this case is after the first component. One might based on this, select only one component. However, one component is probably too few, particularly because we have only explained 37% of the variation. Consider the scree plot based on the standardized variables.
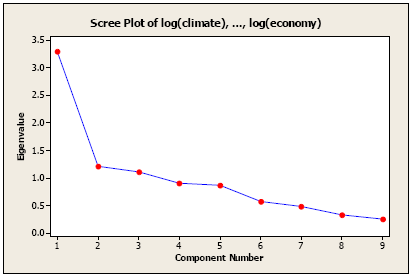
The scree plot for standardized variables (correlation matrix)
Step 2
Next, we can compute the principal component scores using the eigenvectors. This is a formula for the first principal component:
\(\begin{array} \hat{Y}_1 & = & 0.158 \times Z_{\text{climate}} + 0.384 \times Z_{\text{housing}} + 0.410 \times Z_{\text{health}}\\ & & + 0.259 \times Z_{\text{crime}} + 0.375 \times Z_{\text{transportation}} + 0.274 \times Z_{\text{education}} \\ && 0.474 \times Z_{\text{arts}} + 0.353 \times Z_{\text{recreation}} + 0.164 \times Z_{\text{economy}}\end{array}\)
And remember, this is now a function of the standardized data, not of the raw data.
The magnitudes of the coefficients give the contributions of each variable to that component. Because the data have been standardized, they do not depend on the variances of the corresponding variables.
Step 3
Let's look at the coefficients for the principal components. In this case, because the data are standardized, the relative magnitude of each coefficient can be directly assessed within a column. Each column here corresponds with a column in the output of the program labeled Eigenvectors.
| Principal Component | |||||
|---|---|---|---|---|---|
| Variable | 1 | 2 | 3 | 4 | 5 |
| Climate | 0.158 | 0.069 | 0.800 | 0.377 | 0.041 |
| Housing | 0.384 | 0.139 | 0.080 | 0.197 | -0.580 |
| Health | 0.410 | -0.372 | -0.019 | 0.113 | 0.030 |
| Crime | 0.259 | 0.474 | 0.128 | -0.042 | 0.692 |
| Transportation | 0.375 | -0.141 | -0.141 | -0.430 | 0.191 |
| Education | 0.274 | -0.452 | -0.241 | 0.457 | 0.224 |
| Arts | 0.474 | -0.104 | 0.011 | -0.147 | 0.012 |
| Recreation | 0.353 | 0.292 | 0.042 | -0.404 | -0.306 |
| Economy | 0.164 | 0.540 | -0.507 | 0.476 | -0.037 |
Interpretation of the principal components is based on which variables are most strongly correlated with each component. In other words, we need to decide which numbers are large within each column. In the first column, we see that Health and Arts are large. This is very arbitrary. Other variables might have also been included as part of this first principal component.
Component Summaries
- First Principal Component Analysis - PCA1
The first principal component is a measure of the quality of Health and the Arts, and to some extent Housing, Transportation, and Recreation. This component is associated with high ratings on all of these variables, especially Health, and Arts. They are all positively related to PCA1 because they all have positive signs.
- Second Principal Component Analysis - PCA2
The second principal component is a measure of the severity of the crime, the quality of the economy, and the lack of quality education. PCA2 is associated with high ratings of Crime and Economy and low ratings of Education. Here we can see that PCA2 distinguishes cities with high levels of crime and good economies from cities with poor educational systems.
- Third Principal Component Analysis - PCA3
The third principal component is a measure of the quality of the climate and the poorness of the economy. PCA3 is associated with high Climate ratings and low Economy ratings. The inclusion of economy within this component will add a bit of redundancy to our results. This component is primarily a measure of climate and to a lesser extent the economy.
- Fourth Principal Component Analysis - PCA4
The fourth principal component is a measure of the quality of education and the economy and the poorness of the transportation network and recreational opportunities. PCA4 is associated with high Education and Economy ratings and low Transportation and Recreation ratings.
- Fifth Principal Component Analysis - PCA5
The fifth principal component is a measure of the severity of the crime and the quality of housing. PCA5 is associated with high Crime ratings and low housing ratings.
11.7 - Once the Components Are Calculated
11.7 - Once the Components Are CalculatedOne can interpret this component by component. One method of deciding how many components to include is to choose only those that give unambiguous results, i.e., where no variable appears in two different columns as a significant contribution.
We have to make a decision as to what is an important correlation, not necessarily from a statistical hypothesis testing perspective, but from, in this case, an urban-sociological perspective. You have to decide what is important in the context of the problem at hand. This decision may differ from discipline to discipline. In some disciplines such as sociology and ecology, the data tend to be inherently 'noisy', and in this case, you would expect 'messier' interpretations. If you are looking in a discipline such as engineering where everything has to be precise, you might put higher demands on the analysis. You would want to have very high correlations. Principal component analyses are mostly implemented in sociological and ecological types of applications as well as in marketing research.
As before, you can plot the principal components against one another and explore where the data for certain observations lies.
Sometimes the principal component scores will be used as explanatory variables in a regression. Sometimes in regression settings, you might have a very large number of potential explanatory variables and you may not have much of an idea as to which ones you might think are important. You might perform a principal components analysis first and then perform a regression predicting the variables from the principal components themselves. The nice thing about this analysis is that the regression coefficients will be independent of one another because the components are independent of one another. In this case, you actually say how much of the variation in the variable of interest is explained by each of the individual components. This is something that you can not normally do in multiple regression.
One of the problems with this analysis is that the analysis is not as 'clean' as one would like with all of the numbers involved. For example, in looking at the second and third components, the economy is considered to be significant for both of those components. As you can see, this will lead to an ambiguous interpretation in our analysis.
An alternative method of data reduction is Factor Analysis where factor rotations are used to reduce the complexity and obtain a cleaner interpretation of the data.
11.8 - Summary
11.8 - SummaryIn this lesson we learned about:
- The definition of a principal components analysis;
- How to interpret the principal components;
- How to select the number of principal components;
- How to choose between an analysis based on the variance-covariance matrix or the correlation matrix?