11.3 - Example: Places Rated
11.3 - Example: Places RatedExample 11-2: Places Rated
We will use the Places Rated Almanac data (Boyer and Savageau) which rates 329 communities according to nine criteria:
- Climate and Terrain
- Housing
- Health Care & Environment
- Crime
- Transportation
- Education
- The Arts
- Recreation
- Economics
Notes
- The data for many of the variables are strongly skewed to the right.
- The log transformation was used to normalize the data.
Download the text file that contains the data here: places.csv
The SAS program will implement the principal component procedures:
Download the SAS program here: places.sas
View the video explanation of the SAS code.Note: In the upper right-hand corner of the code block you will have the option of copying ( ) the code to your clipboard or downloading ( ) the file to your computer.
options ls=78;
title "PCA - Covariance Matrix - Places Rated";
/* After reading in the places data, the (base 10) log transformations are taken.
* This is an optional step and not required for the pca analysis.
*/
data places;
infile "D:\Statistics\STAT 505\data\places.csv" firstobs=2 delimiter=',';
input climate housing health crime trans educate arts recreate econ id;
climate=log10(climate);
housing=log10(housing);
health=log10(health);
crime=log10(crime);
trans=log10(trans);
educate=log10(educate);
arts=log10(arts);
recreate=log10(recreate);
econ=log10(econ);
run;
/* The princomp procedure performs pca on the places data.
* The cov option specifies results are calculated from the covariance
* matrix, instead of the default correlation matrix.
* The out=a option saves results to a data set named 'a'.
*/
proc princomp data=places cov out=a;
var climate housing health crime trans educate arts recreate econ;
run;
/* The corr procedure is used to calculate pairwise correlations
* between the first 3 principal components and the original variables.
*/
proc corr data=a;
var prin1 prin2 prin3 climate housing health crime trans educate arts
recreate econ;
run;
/* The gplot procedure is used to plot the first 2 principal components.
* axis1 and axis2 options set the plotting window size,
* and these are then set to vertical and horizontal axes, respectively.
*/
proc gplot data=a;
axis1 length=5 in;
axis2 length=5 in;
plot prin2*prin1 / vaxis=axis1 haxis=axis2;
run;
When you examine the output, the first thing that SAS does is provide summary information. There are 329 observations representing the 329 communities in our dataset and 9 variables. This is followed by simple statistics that report the means and standard deviations for each variable.
Below this is the variance-covariance matrix for the data. You should be able to see that the variance reported for the climate is 0.01289.
What we really need to draw our attention to here is the eigenvalues of the variance-covariance matrix. In the SAS output, the eigenvalues are in ranked order from largest to smallest. These values appear in Table 1 below for discussion.
Principal components analysis (covariance matrix)
To perform principal components analysis on the covariance matrix:
- Open the ‘places’ data set in a new worksheet.
- Transform variables. This step is optional but used in the steps below.
- Calc > Calculator
- Highlight and select ‘climate’ to move it to the Store result window.
- In the Expression window, enter LOGTEN( 'climate' ) to apply the (base 10) log transformation to the climate variable.
- Choose OK. The transformed values replace the originals in the worksheet under ‘climate’.
- Repeat sub-steps 1) through 4) above for all variables housing through econ.
- Stat > Multivariate > Principal Components
- Highlight and select climate through econ to move all 9 variables to the Variables window.
- Choose 9 for number of components.
- Check Covariance for Type of Matrix.
- Under Storage, for the Coefficients and Eigenvalues, enter c11 and c12 (or any two unused columns in the worksheet).
- Choose OK and OK again. The results are displayed in the results area and stored in worksheet columns as well.
Data Analysis
Step 1: Examine the eigenvalues to determine how many principal components should be considered:
Table 1. Eigenvalues and the proportion of variation are explained by the principal components.
| Component | Eigenvalue | Proportion | Cumulative |
|---|---|---|---|
| 1 | 0.3775 | 0.7227 | 0.7227 |
| 2 | 0.0511 | 0.0977 | 0.8204 |
| 3 | 0.0279 | 0.0535 | 0.8739 |
| 4 | 0.0230 | 0.0440 | 0.9178 |
| 5 | 0.0168 | 0.0321 | 0.9500 |
| 6 | 0.0120 | 0.0229 | 0.9728 |
| 7 | 0.0085 | 0.0162 | 0.9890 |
| 8 | 0.0039 | 0.0075 | 0.9966 |
| 9 | 0.0018 | 0.0034 | 1.0000 |
| Total | 0.5225 |
If you take all of these eigenvalues and add them up, then you get a total variance of 0.5223.
The proportion of variation explained by each eigenvalue is given in the third column. For example, 0.3775 divided by 0.5223 equals 0.7227, or, about 72% of the variation is explained by this first eigenvalue. The cumulative percentage explained is obtained by adding the successive proportions of variation explained to obtain the running total. For instance, 0.7227 plus 0.0977 equals 0.8204, and so forth. Therefore, about 82% of the variation is explained by the first two eigenvalues together.
Next, we need to look at successive differences between the eigenvalues. Subtracting the second eigenvalue 0.051 from the first eigenvalue, 0.377 we get a difference of 0.326. The difference between the second and third eigenvalues is 0.0232; the next difference is 0.0049. Subsequent differences are even smaller. A sharp drop from one eigenvalue to the next may serve as another indicator of how many eigenvalues to consider.
The first three principal components explain 87% of the variation. This is an acceptably large percentage.
An Alternative Method to determine the number of principal components is to look at a Scree Plot. With the eigenvalues ordered from largest to smallest, a scree plot is the plot of \(\hat{\lambda_i}\) versus i. The number of components is determined at the point beyond which the remaining eigenvalues are all relatively small and of comparable size. The following plot is made in Minitab.
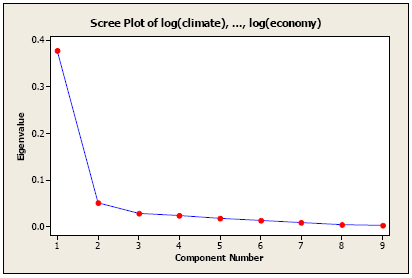
The scree plot for the variables without standardization (covariance matrix)
As you see, we could have stopped at the second principal component, but we continued till the third component. Relatively speaking, the contribution of the third component is small compared to the second component.
Step 2: Next, we compute the principal component scores. For example, the first principal component can be computed using the elements of the first eigenvector:
\begin{align}\hat{Y}_1 & = 0.0351 \times (\text{climate}) + 0.0933 \times (\text{housing}) + 0.4078 \times (\text{health})\\ & + 0.1004 \times (\text{crime}) + 0.1501 \times (\text{transportation}) + 0.0321 \times (\text{education}) \\ & 0.8743 \times (\text{arts}) + 0.1590 \times (\text{recreation}) + 0.0195 \times (\text{economy})\end{align}
In order to complete this formula and compute the principal component for the individual community of interest, plug in that community's values for each of these variables. A fairly standard procedure is to use the difference between the variables and their sample means rather than the raw data. This is known as a translation of the random variables. Translation does not affect the interpretations because the variances of the original variables are the same as those of the translated variables.
The magnitudes of the coefficients give the contributions of each variable to that component. However, the magnitude of the coefficients also depends on the variances of the corresponding variables.