Lesson 13: Canonical Correlation Analysis
Lesson 13: Canonical Correlation AnalysisOverview
Canonical correlation analysis explores the relationships between two multivariate sets of variables (vectors), all measured on the same individual.
Consider, as an example, variables related to exercise and health. On the one hand, you have variables associated with exercise, observations such as the climbing rate on a stair stepper, how fast you can run a certain distance, the amount of weight lifted on a bench press, the number of push-ups per minute, etc. On the other hand, you have variables that attempt to measure overall health, such as blood pressure, cholesterol levels, glucose levels, body mass index, etc. Two types of variables are measured and the relationships between the exercise variables and the health variables are of interest.
As a second example consider variables measured on environmental health and environmental toxins. A number of environmental health variables such as frequencies of sensitive species, species diversity, total biomass, the productivity of the environment, etc. may be measured and a second set of variables on environmental toxins are measured, such as the concentrations of heavy metals, pesticides, dioxin, etc.
For a third example consider a group of sales representatives, on whom we have recorded several sales performance variables along with several measures of intellectual and creative aptitude. We may wish to explore the relationships between the sales performance variables and the aptitude variables.
One approach to studying relationships between the two sets of variables is to use canonical correlation analysis which describes the relationship between the first set of variables and the second set of variables. We do not necessarily think of one set of variables as independent and the other as dependent, though that may potentially be another approach.
Objectives
- Carry out a canonical correlation analysis using SAS (Minitab does not have this functionality);
- Assess how many canonical variate pairs should be considered;
- Interpret canonical variate scores;
- Describe the relationships between variables in the first set with variables in the second set.
13.1 - Setting the Stage for Canonical Correlation Analysis
13.1 - Setting the Stage for Canonical Correlation AnalysisWhat motivates canonical correlation analysis?
It is possible to create pairwise scatter plots with variables in the first set (e.g., exercise variables), and variables in the second set (e.g., health variables). But if the dimension of the first set is p and that of the second set is q, there will be pq such scatter plots, it may be difficult, if not impossible, to look at all of these graphs together and interpret the results.
Similarly, you could compute all correlations between variables from the first set (e.g., exercise variables), and variables in the second set (e.g., health variables), however, interpretation is difficult when pq is large.
Canonical Correlation Analysis allows us to summarize the relationships into fewer statistics while preserving the main facets of the relationships. In a way, the motivation for canonical correlation is very similar to principal component analysis. It is another dimension-reduction technique.
Canonical Variates
Let's begin with the notation:
We have two variables \(X\) and \(Y\).
Suppose we have p variables in set 1: \(\textbf{X} = \left(\begin{array}{c}X_1\\X_2\\\vdots\\ X_p\end{array}\right)\)
and suppose we have q variables in set 2: \(\textbf{Y} = \left(\begin{array}{c}Y_1\\Y_2\\\vdots\\ Y_q\end{array}\right)\)
We select X and Y based on the number of variables in each set so that \(p ≤ q\). This is done for computational convenience.
We look at linear combinations of the data, similar to principal components analysis. We define a set of linear combinations named U and V. U corresponds to the linear combinations from the first set of variables, X, and V corresponds to the second set of variables, Y. Each member of U is paired with a member of V. For example, \(U_{1}\) below is a linear combination of the p X variables and \(V_{1}\) is the corresponding linear combination of the q Y variables. Similarly, \(U_{2}\) is a linear combination of the p X variables, and \(V_{2}\) is the corresponding linear combination of the q Y variables. And, so on...
\begin{align} U_1 & = a_{11}X_1 + a_{12}X_2 + \dots + a_{1p}X_p \\ U_2 & = a_{21}X_1 + a_{22}X_2 + \dots + a_{2p}X_p \\ & \vdots \\ U_p & = a_{p1}X_1 +a_{p2}X_2 + \dots +a_{pp}X_p\\ & \\ V_1 & = b_{11}Y_1 + b_{12}Y_2 + \dots + b_{1q}Y_q \\ V_2 & = b_{21}Y_1 + b_{22}Y_2 + \dots +b_{2q}Y_q \\ & \vdots \\ V_p & = b_{p1}Y_1 +b_{p2}Y_2 + \dots +b_{pq}Y_q\end{align}
Thus define
\((U_i, V_i)\)
as the \(i^{th}\) canonical variate pair. ( \(U_{1}\), \(V_{1}\)) is the first canonical variate pair, similarly ( \(U_{2}\), \(V_{2}\)) would be the second canonical variate pair, and so on. With \(p ≤ q\) there are p canonical covariate pairs.
We hope to find linear combinations that maximize the correlations between the members of each canonical variate pair.
We compute the variance of \(U_{i}\) variables with the following expression:
\(\text{var}(U_i) = \sum\limits_{k=1}^{p}\sum\limits_{l=1}^{p}a_{ik}a_{il}cov(X_k, X_l)\)
The coefficients \(a^{i1}\) through \(a^{ip}\) that appear in the double sum are the same coefficients that appear in the definition of \(U_{i}\). The covariances between the \(k^{th}\) and \(l^{th}\) X-variables are multiplied by the corresponding coefficients \(a^{ik}\) and \(a^{il}\) for the variate \(U_{i}\).
Similar calculations can be made for the variance of \(V_{j}\) as shown below:
\(\text{var}(V_j) = \sum\limits_{k=1}^{p} \sum\limits_{l=1}^{q} b_{jk}b_{jl}\text{cov}(Y_k, Y_l)\)
The covariance between \(U_{i}\) and \(V_{j}\) is:
\(\text{cov}(U_i, V_j) = \sum\limits_{k=1}^{p} \sum\limits_{l=1}^{q}a_{ik}b_{jl}\text{cov}(X_k, Y_l)\)
The correlation between \(U_{i}\) and \(V_{j}\) is calculated using the usual formula. We take the covariance between the two variables and divide it by the square root of the product of the variances:
\(\dfrac{\text{cov}(U_i, V_j)}{\sqrt{\text{var}(U_i) \text{var}(V_j)}}\)
The canonical correlation is a specific type of correlation. The canonical correlation for the \(i^{th}\) canonical variate pair is simply the correlation between \(U_{i}\) and \(V_{i}\):
\(\rho^*_i = \dfrac{\text{cov}(U_i, V_i)}{\sqrt{\text{var}(U_i) \text{var}(V_i)}} \)
This is the quantity to maximize. We want to find linear combinations of the X's and linear combinations of the Y's that maximize the above correlation.
Canonical Variates Defined
Let us look at each of the p canonical variates pair individually.
First canonical variate pair: \( \left( U _ { 1 } , V _ { 1 } \right)\):
The coefficients \(a_{11}, a_{12}, \dots, a_{1p}\) and \(b_{11}, b_{12}, \dots, b_{1q}\) are selected to maximize the canonical correlation \(\rho^*_1\) of the first canonical variate pair. This is subject to the constraint that variances of the two canonical variates in that pair are equal to one.
\(\text{var}(U_1) = \text{var}(V_1) = 1\)
This is required to obtain unique values for the coefficients.
Second canonical variate pair: \( \left( U _ { 2 } , V _ { 2 } \right)\)
Similarly we want to find the coefficients \(a_{21}, a_{22}, \dots, a_{2p}\) and \(b_{21}, b_{22}, \dots, b_{2q}\) that maximize the canonical correlation \(\rho^*_2\) of the second canonical variate pair, \( \left( U _ { 2 } , V _ { 2 } \right)\). Again, we will maximize this canonical correlation subject to the constraint that the variances of the individual canonical variates are both equal to one. Furthermore, we require the additional constraints that \( \left( U _ { 1 } , U _ { 2 } \right)\), and \( \left( V_{1} , V_{2} \right)\) are uncorrelated. In addition, the combinations \( \left( U_{1} , V_{2} \right)\) and \( \left( U_{2} , V_{1} \right)\) must be uncorrelated. In summary, our constraints are:
\(\text{var}(U_2) = \text{var}(V_2) = 1\),
\(\text{cov}(U_1, U_2) = \text{cov}(V_1, V_2) = 0\),
\(\text{cov}(U_1, V_2) = \text{cov}(U_2, V_1) = 0\).
Basically, we require that all of the remaining correlations equal zero.
This procedure is repeated for each pair of canonical variates. In general, ...
\( i^{th} \) canonical variate pair: \( \left( U _ { i } , V _ { i } \right)\)
We want to find the coefficients \(a_{i1}, a_{i2}, \dots, a_{ip}\) and \(b_{i1}, b_{i2}, \dots, b_{iq}\) that maximize the canonical correlation \(\rho^*_i\) subject to the constraints that
\(\text{var}(U_i) = \text{var}(V_i) = 1\),
\(\text{cov}(U_1, U_i) = \text{cov}(V_1, V_i) = 0\),
\(\text{cov}(U_2, U_i) = \text{cov}(V_2, V_i) = 0\),
\(\vdots\)
\(\text{cov}(U_{i-1}, U_i) = \text{cov}(V_{i-1}, V_i) = 0\),
\(\text{cov}(U_1, V_i) = \text{cov}(U_i, V_1) = 0\),
\(\text{cov}(U_2, V_i) = \text{cov}(U_i, V_2) = 0\),
\(\vdots\)
\(\text{cov}(U_{i-1}, V_i) = \text{cov}(U_i, V_{i-1}) = 0\).
Again, requiring all of the remaining correlations to be equal to zero.
Next, let's see how this is carried out in SAS...
13.2 - Example: Sales Data
13.2 - Example: Sales DataExample 13-1: Sales
The example data comes from a firm that surveyed a random sample of n = 50 of its employees in an attempt to determine which factors influence sales performance. Two collections of variables were measured:
- Sales Performance:
- Sales Growth
- Sales Profitability
- New Account Sales
- Test Scores as a Measure of Intelligence
- Creativity
- Mechanical Reasoning
- Abstract Reasoning
- Mathematics
There are p = 3 variables in the first group relating to Sales Performance and q = 4 variables in the second group relating to Test Scores.
Download the text file containing the data here: sales.csv
Canonical Correlation Analysis is carried out in SAS using a canonical correlation procedure that is abbreviated as cancorr. Let's look at how this is carried out in the SAS Program below
Download the SAS program here: sales.sas or click on the copy icon inside Explore the Code.
Note: In the upper right-hand corner of the code block you will have the option of copying ( ) the code to your clipboard or downloading ( ) the file to your computer.
options ls=78;
title "Canonical Correlation Analysis - Sales Data";
data sales;
infile "D:\Statistics\STAT 505\data\sales.csv" firstobs=2 delimiter=',';
input growth profit new create mech abs math;
run;
/* The vprefix and wprefix options specify names to separate the two
* sets of variables for the analysis.
* The vname and wname options are more descriptive string names to be used
* to describe the two sets of variables.
* The var and with statements specify which variables go into each set.
* They are referred to by the terms used in the vprefix and wprefix, respectively.
*/
proc cancorr data=sales out=canout
vprefix=sales vname="Sales Variables"
wprefix=scores wname="Test Scores";
var growth profit new;
with create mech abs math;
run;
/* This plots the first canonical pair as a 2d scatterplot.
* Other canonical pairs can also be plotted by changing
* the variables used in the plot statement.
*/
proc gplot data=canout;
axis1 length=3 in;
axis2 length=4.5 in;
plot sales1*scores1 / vaxis=axis1 haxis=axis2;
symbol v=J f=special h=2 i=r color=black;
run;
13.3. Test for Relationship Between Canonical Variate Pairs
13.3. Test for Relationship Between Canonical Variate PairsLet's first determine if there is any relationship between the two sets of variables at all. Perhaps the two sets of variables are completely unrelated to one another and independent!
To test for independence between the Sales Performance and the Test Score variables, first, consider a multivariate multiple regression model where we predict the Sales Performance variables from the Test Score variables. In this general case, we have p multiple regressions, each multiple regression predicting one of the variables in the first group ( X variables) from the q variables in the second group (Y variables).
\begin{align} X_1 & = \beta_{10} + \beta_{11}Y_1 +\beta_{12}Y_2 + \dots +\beta_{1q}Y_q + \epsilon_1 \\ X_2 & = \beta_{20}+ \beta_{21}Y_1 + \beta_{22}Y_2 + \dots +\beta_{2q}Y_q + \epsilon_2 \\ & \vdots \\ X_p & = \beta_{p0} + \beta_{p1}Y_1 + \beta_{p2}Y_2 + \dots + \beta_{pq}Y_q + \epsilon_p \end{align}
In our example, we have multiple regressions predicting the p = 3 sales variables from the q = 4 test score variables. We wish to test the null hypothesis that these regression coefficients (except for the intercepts) are all equal to zero. This would be equivalent to the null hypothesis that the first set of variables is independent of the second set of variables.
\(H_0\colon \beta_{ij} = 0;\) \( i = 1,2, \dots, p; j = 1,2, \dots, q\)
This is carried out using Wilks lambda. The results of this are found on page 1 of the output of the SAS Program.
Test of H0: The canonical correlations in the current row and all that follow are zero
| Likelihood Ratio |
Approximate F Value |
Num DF | Den DF | Pr > F | |
|---|---|---|---|---|---|
| 1 | 0.00214847 | 87.39 | 12 | 114.06 | <.0001 |
| 2 | 0.19524127 | 18.53 | 6 | 88 | <.0001 |
| 3 | 0.85284669 | 3.88 | 2 | 45 | 0.0278 |
SAS reports Wilks lambda \(\Lambda = 0.00215 ; F = 87.39 ; d . f = 12,114 ; p < 0.0001\). Wilks lambda is a ratio of two variance-covariance matrices (raised to a certain power). If the values of these statistics are large (small p-value), then we reject the null hypothesis. In our example, we reject the null hypothesis that there is no relationship between the two sets of variables and conclude that the two sets of variables are dependent. Note also that the above null hypothesis is also equivalent to testing the null hypothesis that all p canonical variate pairs are uncorrelated, or
\(H_0\colon \rho^*_1 = \rho^*_2 = \dots = \rho^*_p = 0 \)
Because Wilks lambda is significant and the canonical correlations are ordered from largest to smallest, we can conclude that at least \(\rho^*_1 \ne 0\).
We may also wish to test the hypothesis that the second or the third canonical variate pairs are correlated. We can do this in successive tests. Next, test whether the second and third canonical variate pairs are correlated...
\(H_0\colon \rho^*_2 = \rho^*_3 = 0\)
We can look again at the SAS output above. In the second row for the likelihood ratio test statistic we find \(L ^ { \prime } = 0.19524 ; F = 18.53 ; d . f = 6,88 ; p < 0.0001\). From this test we can conclude that the second canonical variate pair is correlated, \(\rho^*_2 \ne 0\).
Finally, we can test the significance of the third canonical variate pair.
\(H_0\colon \rho^*_3 = 0\)
The third row of the SAS output contains the likelihood ratio test statistic \(L ^ { \prime } = 0.8528 ; F = 3.88 ; d . f = 2,45 ; p = 0.0278\). This is also significant and so we conclude that the third canonical variate pair is correlated.
All three canonical variate pairs are significantly correlated and dependent on one another. This suggests that we may summarize all three pairs. In practice, these tests are carried out successively until you find a non-significant result. Once a non-significant result is found, you stop. If this happens with the first canonical variate pair, then there is not sufficient evidence of any relationship between the two sets of variables and the analysis may stop.
If the first pair shows significance, then you move on to the second canonical variate pair. If this second pair is not significantly correlated then stop. If it was significant you would continue to the third pair, proceeding in this iterative manner through the pairs of canonical variates testing until you find non-significant results.
13.4 - Obtain Estimates of Canonical Correlation
13.4 - Obtain Estimates of Canonical CorrelationNow that we rejected the hypotheses of independence, the next step is to obtain estimates of canonical correlation.
The estimated canonical correlations are found at the top of page 1 in the SAS output as shown below:
Canonical Correlation Analysis
| Canonical Correlation |
Adjusted Canonical Correlation |
Approximate Standard Error |
Squared Canonical Correlation |
|
|---|---|---|---|---|
| 1 | 0.994483 | 0.994021 | 0.001572 | 0.988996 |
| 2 | 0.878107 | 0.872097 | 0.032704 | 0.771071 |
| 3 | 0.383606 | 0.366795 | 0.121835 | 0.147153 |
The squared values of the canonical variate pairs, found in the last column, can be interpreted much in the same way as \(r^{2}\) values are interpreted.
We see that 98.9% of the variation in \(U_{1}\) is explained by the variation in \(V_{1}\), and 77.11% of the variation in \(U_{2}\) is explained by \(V_{2}\), but only 14.72% of the variation in \(U_{3}\) is explained by \(V_{3}\). These first two are very high canonical correlations and suggest that only the first two canonical correlations are important.
One can actually see this from the plots that SAS generates. The first canonical variate for sales is plotted against the first canonical variate for scores in the scatter plot for the first canonical variate pair:
Canonical Correlation Analysis - Sales Data
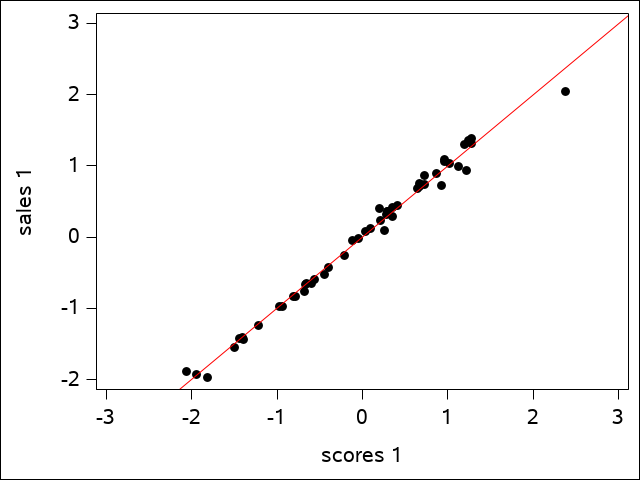
The regression line shows how well the data fits. The plot of the second canonical variate pair is a bit more scattered, but is still a reasonably good fit:
Canonical Correlation Analysis - Sales Data
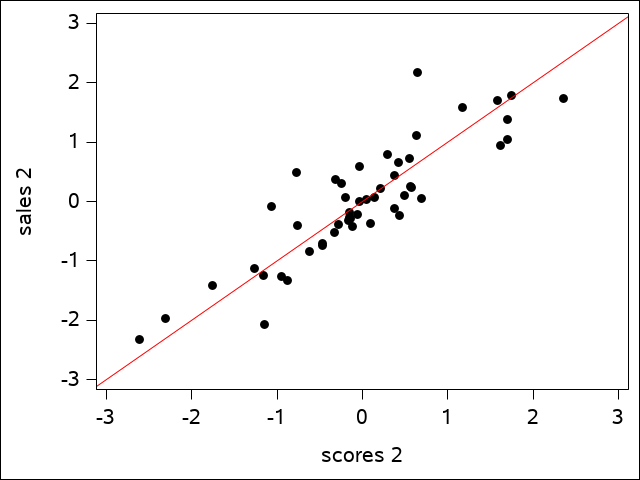
A plot of the third pair would show little of the same kind of fit. We may refer to only the first two canonical variate pairs from this point on based on the observation that the third squared canonical correlation value is so small.
13.5 - Obtain the Canonical Coefficients
13.5 - Obtain the Canonical CoefficientsPage 2 of the SAS output provides the estimated canonical coefficients \(\left(a_{ij}\right)\) for the sales variables:
Canonical Correlation Analysis
Raw Canonical Coefficients for the Sales Variables
| \(\bf{U}_1\) sales1 | sales2 | sales3 | |
|---|---|---|---|
| growth | 0.0623778783 | -0.174070306 | -0.377152934 |
| profit | 0.020925642 | 0.2421640883 | 0.1035150082 |
| net | 0.0782581746 | -0.23829403 | 0.3834150736 |
Using the coefficient values in the first column, the first canonical variable for sales is determined using the following formula:
\(U_1 = 0.0624X_{growth}+0.0209X_{profit}+0.0783X_{new}\)
Likewise, the estimated canonical coefficients \(\left(b_{ij}\right)\) for the test scores are located in the next table in the SAS output:
Raw Canonical Coefficients for the Test Scores
| \(\bf{V}_1\) scores1 | scores2 | scores3 | |
|---|---|---|---|
| create | 0.0697481411 | -0.192391323 | 0.2465565859 |
| mech | 0.0307382997 | 0.201574382 | -0.141895279 |
| abs | 0.0895641768 | -0.495763258 | -0.280224053 |
| math | 0.0628299739 | 0.0683160677 | 0.0113325936 |
Using the coefficient values in the first column, the first canonical variable for test scores is determined using a similar formula:
\(V_1 = 0.0697Y_{create}+0.0307Y_{mech}+0.0896Y_{abstract}+0.0628Y_{math}\)
In both cases, the magnitudes of the coefficients give the contributions of the individual variables to the corresponding canonical variable. However, just like in principal components analysis, these magnitudes also depend on the variances of the corresponding variables. Unlike principal components analysis, however, standardizing the data has no impact on the canonical correlations.
13.6 - Interpret Each Component
13.6 - Interpret Each ComponentTo interpret each component, we must compute the correlations between each variable and the corresponding canonical variate.
-
The correlations between the sales variables and the canonical variables for Sales Performance are found at the top of the fourth page of the SAS output in the following table:
Correlations Between the Sales Variables and Their Canonical Variables
sales1 sales2 sales3 growth 0.9799 0.0006 -0.1996 profit 0.9464 0.3229 0.0075 new 0.9519 -0.1863 0.2434 Looking at the first canonical variable for sales, we see that all correlations are uniformly large. Therefore, you can think of this canonical variate as an overall measure of Sales Performance. For the second canonical variable for Sales Performance, none of the correlations are particularly large, and so, this canonical variable yields little information about the data. Again, we had decided earlier not to look at the third canonical variate pairs.
A similar interpretation can take place with the Test Scores.
-
b. The correlations between the test scores and the canonical variables for Test Scores are also found in the SAS output:
Correlations Between the Test Scores and Their Canonical Variables
scores1 scores2 scores3 create 0.6383 -0.2157 0.6514 mech 0.7212 0.2376 -0.677 abs 0.6472 -0.5013 -0.5742 math 0.9441 0.1975 -0.0942 Because all correlations are large for the first canonical variable, this can be thought of as an overall measure of test performance as well, however, it is most strongly correlated with mathematics test scores. Most of the correlations with the second canonical variable are small. There is some suggestion that this variable may be negatively correlated with abstract reasoning.
c. Putting (a) and (b) together, we see that the best predictor of sales performance is mathematics test scores as this indicator stands out the most.
13.7 - Reinforcing the Results
13.7 - Reinforcing the ResultsThese results are further reinforced by looking at the correlations between each set of variables and the opposite group of canonical variates.
- The correlations between the sales variables and the first canonical variate for test scores are found on page 4 of the SAS output:
Correlations Between the Sales Variables and the Canonical Variables of the Test Scores
scores1 scores2 scores3 growth 0.9745 0.0006 -0.0766 profit 0.9412 0.2835 0.0029 new 0.9466 -0.1636 0.0934 We can see that all three of these correlations are strong and show a pattern similar to that with the canonical variate for sales. The reason for this is obvious: The first canonical correlation is very high.
-
The correlations between the test scores and the first canonical variate for sales are also in the SAS output:
Correlations Between the Test Scores and the Canonical Variables of the Sales Variables
sales1 sales2 sales3 create 0.6348 -0.1894 0.2499 mech 0.7172 0.2086 -0.0260 abs 0.6437 -0.4402 -0.2203 math 0.9389 0.1735 -0.0361 Note! These also show a pattern similar to that with the canonical variate for test scores. Again, this is because the first canonical correlation is very high. -
These results confirm that sales performance is best predicted by mathematics test scores.
13.8 - Summary
13.8 - SummaryIn this lesson we learned about:
- How to test for independence between two sets of variables
- How to determine the number of significant canonical variate pairs
- How to compute the canonical variates from the data
- How to interpret each member of a canonical variate pair using its correlations with the member variables
- How to use the results of canonical correlation analysis to describe the relationships between two sets of variables